基于行为经济学视角的国企技能类员工薪酬改革模式探讨

邓灿 蔡雨琴 罗俊 李钦 樊昕 中国电科芯片技术研究院

一、国企薪酬改革的背景与目的

面对日益严峻的竞争压力，国有企业老旧的薪酬系统需要重新设计以迎合市场化的需求。目前多数国有企业的薪酬平均主义现象依旧存在，一方面是岗位之间的工资缺乏级差，另一方面是不同的工作量对应的工资也没有区分度， “大锅饭” 的环境使得工作量多的员工产生有失公平的感受。由于薪酬发放制度并没有依据按劳分配的原则，也使得当前的薪酬制度缺乏内部激励性。因此，国企固有的薪酬发放制度亟待改善，依据 “效率优先、兼顾公平、按劳分配” 的原则，提升员工的公平感和工作积极性，从而提升企业的劳动生产率[1]。

笔者所在的某国有企业，技能岗位占比超过公司总人数60%，工作主要涵盖产品的生产、检验和测试等环节，数量庞大的技能岗位可以说是公司的 “神经末梢” 。尽管这些岗位的人员往往远离公司的技术与权力中心，但他们的工作状态将直接决定公司的生产效率。根据以上背景，本文将基于行为经济学的视角分析目前主流的薪酬改革模式的效用，通过建立数学模型分析不同模式的利弊，为国企技能类员工的薪酬改革提供参考。

二、国企技能类员工薪酬模式的设定

1.几种典型的薪酬改革模式

根据各大企业实践，薪酬套改模式主要可分为以下四大类：现有水平确定法、单因素确定法、个人优势确定法和综合因素确定法。

现有水平确定法是依据员工在旧薪酬模式下的收入总额，根据考核指标确定新模式的收入；单因素确定法是以某单一因素来确定员工薪酬等级；个人优势确定法是单因素确定法的丰富化，通过取不同因素测算结果的最高档或加权平均值来确定员工薪酬等级；综合因素确定法则是在个人优势确定法的基础上考虑学历、资质、工龄等历史因素，以确定员工薪酬等级。

2.典型国企旧有薪酬模式

笔者所在的单位，员工的薪酬主要由学历工资、岗位工资、职称工资，工龄工资和绩效工资组成，在以上五大类工资中，由于员工的学历、岗位、职称和工龄相对固定，故绩效工资是管理者调节员工薪酬的唯一途径，这也符合绩效工资的定义，即以对员工工作绩效的有效考核为基础，实现工资与考核结果的挂钩。

但在笔者所在单位的旧有薪酬模式中，对于技能类员工的绩效评估并没有一套清晰且明确的考核机制，工作量因素并没有精确地纳入绩效的核算中，其最显著的特点就是同工不同酬，员工的绩效工资与其当前工作量的关联度不高，而更多地与其历史工资水平挂钩，这就违背了绩效工资由工作绩效表现决定的初衷。这种由历史工资水平决定现有工资水平的模式会降低老员工工作的积极性，因为即使他们减少自己的工作输出他们的绩效收入也不会受到什么影响。在新古典主义经济学的理性人假设下，当前的绩效制度会诱使老员工降低其产出，该行为会减损公司的劳动生产率和产能，因此，旧有的绩效制度需要改革。

本文将详细阐述技能类员工的改革方案，采用上文提到的 “单因素确定法” 来决定员工的薪酬，而决定技能类员工的薪酬的单因素为其工作量数值。

3.以工作量为本位的技能岗位绩效分配方案

技能岗位主要包括生产、检验和测试等流程，是一种按批次计件的重复工作模式。因此，通过计算技能类员工的工作量总量来核算其工作绩效是一种合理的考核方式。通过衡量不同工序的工作难度和单批次工作时间，可以设计出一套涵盖了不同工序的工作量计算系统，通过加权求和的方式即可得到技能类员工在某一统计周期内的工作总量。

常见的工作量分布有正态分布和指数分布两种，对于一个企业和团队而言，指数分布的工作量分布比正态分布更好。因为正态分布的特点在于其随机性，对于一个团队而言，成员工作量的随机分布说明其对成员缺乏管控，整个团队处于一种无序状态；而指数分布则是一种择优选择性的分布，说明团队具有良好的管理[2]。

为了实现工作量从正态分布向指数分布的进化，有序的制度和有效的激励是关键。本文的重点在于研究如何进行有效的激励，下文中的数学分析将探讨在团队总绩效不变的情况下，如何设计基于工作量的绩效发放模型激励员工提高其工作量。

三、薪酬改革数学模型

1.薪酬改革范围边界

笔者所在单位的薪酬套改原则是在保持薪酬总额不变的情况下改变员工绩效的分配，针对以上前提，笔者将针对不同的薪酬改革模式建立数学模型，从而分析比较不同改革模式引发的效用变化。由于在薪酬改革中管理者只有调整绩效算法的权限，因此在本文设计的效用模型中，将只纳入绩效工资，不考虑其他类别的工资。

2.收入效用函数

根据财富的边际效用递减原理，人对于财富的占有越多越好，但效用的增加速度会随财富增加减少，即以财富为自变量的效用函数一阶导数大于0，而二阶导数小于0，常见的效用函数为幂次介于0 到1 之间的幂函数[3]，因此员工绩效工资的效用为：

其中，V(y)为绩效效用，y 为绩效工资，b 为财富效用系数，b ∈ (0, 1)，本文中取0.95。

作为员工，其通过工作量获取绩效，工作量即为其付出的成本，因此该效用应该为负数，员工付出工作量的效用首先会与员工个人的工作量绝对值相关[4]，与此同时，在一个群体中，一个员工对于其个体工作效用的评估也会与其工作量的相对值相关。工作量相对值即某员工工作量与其所在班组人均工作量的比值。人们普遍有高估自己工作量和低估他人工作量的心理趋势[5]，不妨假设相对工作量是以指数的形式影响工作量的实际效用，因此，可以设员工的工作量效用为：

员工通过付出工作量获取绩效工资，根据礼物交换模型[6]，在该交换行为中，员工的效用为：

其中，V(y, x)为绩效-工作量总效用，c 和d 为大于0 的系数，本文中均取1。

3.几种绩效-工作量对应函数介绍

表1 列明了四种绩效-工作量对应关系：

表1 不同类型绩效-工作量对应算法

通过上述公式算出员工的绩效工资y 后，即可将绩效工资y 和工作量x 代入到式（3）中计算员工的绩效-工作量总效用。

四、模拟计算

1.背景参数设定

基于上述的函数，将模拟一个有200 位技能类岗位员工的绩效-工作量效用，模拟中的总绩效薪酬固定为80 万元人民币，即人均绩效为4000 元人民币。

2.正态分布工作量的效用模拟

通过随机数生成程序生成一组200 个平均值为100、标准差为25 的正态分布随机数，作为该部门员工的工作量绝对值，将其分别代入表1 中的算法得到其在不同绩效-工作量关系下的绩效工资，并分别计算出不同绩效工资对应的绩效-工作量总效用，模拟结果如下：

图1 展示了四种不同的绩效分配模式下效用-工作量分布曲线，四种分配模式的模拟结果的曲线形态相似，均为在模拟区间范围内存在极大值的凸性函数，但极大值出现的位点和凸性则有所差异。其中，对数增强关系的分布曲线凸性最强，即效用在递增区间的平均增长率最大，随后依次是线性关系、1/2 线性关系和对数关系。同时可以发现，四种发放模式的分布曲线中，凸性越强的曲线，效用的极大值越高，效用极大值对应的工作量也越大，这也意味着凸性更强的效用曲线，其不仅效用在递增区间的增幅更大，还有着范围更大的递增区间和效用极值。四条分布曲线定量的数据点如表2：

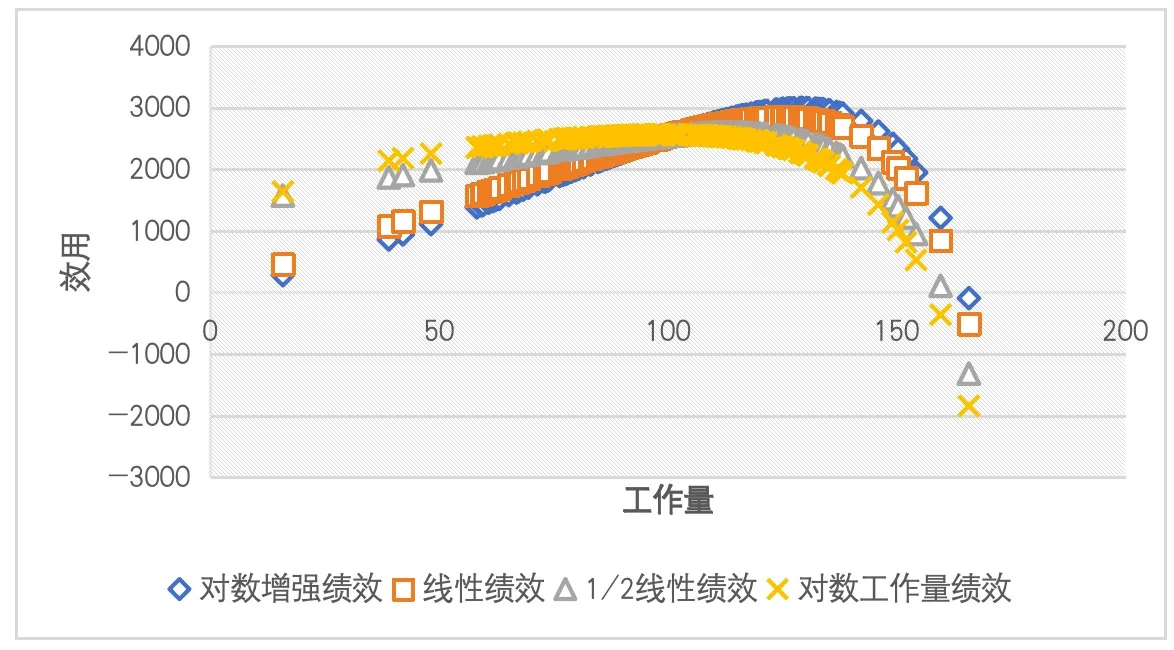
图1 不同绩效分配模式下效用-工作量曲线

表2 基于正态分布工作量的绩效效用模拟结果重要数据点

这四条曲线都在模拟区间内呈凸性，极大值在极值点出现。其中对数关系绩效分配在工作量为99.31时取得效用极大值，而模拟样本的均值为100，因此可以得出对数关系绩效分配无法有效激励工作量呈正态分布的团队。而其他三种绩效分配算法下，效用极大值点对应的工作量均超过团队平均值，因此这三种模式具备激励效果，激励效果的强度依次是对数增强关系、线性关系和1/2 线性关系，考虑到样本数据的标准差为25，根据正态分布的概率分布函数，有约84%的样本会落在区间(0, 125)内，在三种有激励效果的分配模式中，线性关系和对数增强关系的效用极大值点对应的工作量均大于125，即保证了84%以上的样本处在总效用随工作量递增的区间内，是激励效果较好的分配模式，而1/2 线性关系的效用极大值点对应的工作量仅为113.71，激励效果稍逊。四种分配模式下，对数关系的效用极大值最小，为2560.84，对数增强关系的效用极大值最大，为2991.62，故四种模式下效用极大值极差为430.78；至于四种模式下的效用均值，则是对数关系的效用均值最大，为2381.31，对数增强关系的效用均值最小，为2376.03，故四种模式下效用均值的极差为5.28，远小于效用极大值的极差。

由上述数据可以看出，对数关系、1/2 线性关系、线性关系和对数增强关系的效用激励是依次增强的，线性关系和对数增强关系由于能保证超过84%以上的样本处在效用递增区间内，因此是值得推荐的绩效分配模式。与此同时，可以看到尽管使用更强激励效应的分配模式会略微降低团队的效用均值，但影响的幅度极低，几乎可忽略不计。因此，针对工作量呈正态分布的团体，采用线性关系或对数增强关系的绩效分配模式可在几乎维持整体效用不变的情况下有效地激励员工提升工作量。

3.指数分布工作量的效用模拟

由上文所述，工作量呈现指数分布的团队具有更高的有序性，说明了管理的有效性。不妨假设上述呈指数分布的团队通过有效的管理，规定了工作量的下限值为70，而工作量与下限值的差值则呈现指数分布。工作量分布由构造的指数函数计算得出，其公式如下：

其中，x 为工作量，a 为指数分布量，a 服从于λ=2 的指数分布。

基于上述指数分布的概率密度函数，当满足上述分布的工作量取值在(70, 150)区间内时，其均值约为100。通过随机数模拟生成了200 个在区间(70, 150)均值为100 且满足指数分布的数字，将其作为指数分布工作量的模拟值，并将其代入到效用函数中计算绩效-工作量效用，模拟结果与正态分布工作量的模拟结果类似，指数分布下四种分配模式的效用-工作量曲线在模拟区间内也是呈现凸性的，且四种分配模式的曲线定性特征与正态分布的模拟结果相同，模拟结果的重要数据点如表3 所示：

表3 基于指数分布工作量的绩效效用模拟结果重要数据点

四种分配模式的递增和递减区间在两种分布下几乎相同，不论是正态分布还是指数分布，对数关系绩效分配都不具有激励效果，1/2 线性关系分配激励效果较弱，线性关系分配激励效果较强，而对数增强关系的激励效果最强。四种分配模式的效用极大值在两种分布模式下也几乎相同，而效用均值则是在指数分布下更大，四种分配模式在指数分布下的效用均值要比正态分布下的效用均值高约1.27%，这说明了指数分布相对于正态分布的优越性，因为它兼顾了整体的利益和个体的效用。

五、结语

国企技能类员工薪酬改革的目的在于提升员工工作的积极性，为其增加工作量赋予充分动力。根据效用模型，采用线性绩效分配或对数增强绩效分配的模式能有效激励大部分员工提升自己的工作量。除了有效地薪酬激励以外，管理层也需要通过有效地管理将团体的工作量分布由无序的正态分布转换到有序的指数分布上，这个过程不仅能保障团队的生产力，还能提升个体的平均效用，是一个双赢的优化措施。