异中求同显关联 由表及里见演绎
2023-11-21叶青
叶青

摘要:经历演绎推理的过程是培养学生严谨思考,学会辩证看待事物的重要途径之一。教师应以反思教学困境为契机,梳理教材和学情,在此基础上以图形的边角为切入点,带领学生经历证据提炼、论证以及梳理的过程,使其在触及本质的推理表达中不断发展演绎推理,逐渐养成理性的思考方式,形成对立统一的辩证思维。
关键词:四边形的认识;演绎推理;关联视角
推理是数学思维的主要表现之一,学生要形成“会用数学思维思考现实世界”的核心素养,离不开推理意识的培育与发展。推理可分为从特殊走向一般的合情推理和从一般走向特殊的演绎推理。当前,小学阶段的推理教学更多地将关注点落在了合情推理的渗透上,演绎推理的教学则主要集中于初中阶段和高中阶段。实际上,小学阶段许多知识点的教学背后也暗含着演绎推理的思想,亟待教师挖掘和发现。
一、置身课堂,深入思考,直面波折的教学过程
研磨人教版数学教材三年级上册“四边形的认识”一课时遇到的一些问题,引发了笔者对演绎推理教学的深度思考。
(一)眼见就误以为实:缺乏理性验证的意识
在图形的特征验证时,学生普遍暴露出一个问题:疲于动手实证。学生认为自己一眼便能辨认出这个图形是否是长方形或正方形,根本不需要这般繁琐且费时的验证。另外,在验证的过程中,个别学生会在测量出一条边的长度之后,直接写出对边或剩余三边的长度,把特征的验证与特征的应用混淆。可见,学生并不理解验证的意义,在推理认知时缺少严谨的思维模式。
(二)见树木不见树林:缺失立足关联的视角
认识与理解长方形和正方形两者的特殊关系是教学中难以突破的点。由于直观视觉下两者形状的不同给学生带来了强烈的视觉冲击,使得多数学生对“正方形是不是长方形”这一问题的思考,只会站在对立的视角观察分析。即,从特征的区别而言,学生能够明确分辨两者的不同,但对两者关系缺少了关联视角下的认识,也就是关注“异”忽视“同”。
二、全局视角,深度剖析,探寻关键的思想理念
滲透重论据、讲逻辑的演绎推理能够有效促进学生理性思维的成长,助力其辩证思维的萌发,是打破教学困境的有效途径。寻觅与凸显教材中蕴藏的演绎推理,聚焦与把脉学生的学习起点则是探索新模式教学的关键。
(一)为“源”而理,着眼整体联系
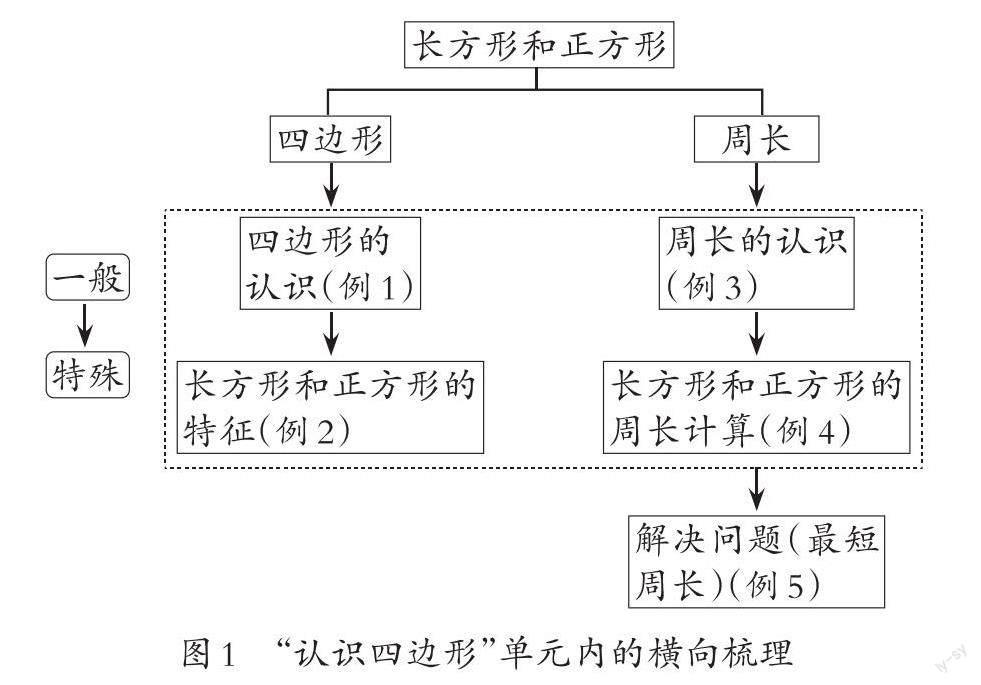
笔者首先对“认识四边形”这一内容进行了单元内的横向梳理(见图1)。该课是人教版数学教材三年级上册第7单元“长方形和正方形”的教学内容,这一单元的教学分为四边形和周长两部分:四边形→长方形→正方形,四边形周长→长方形周长→正方形周长。可以发现这两条教学主线都是从一般走向特殊,这实际上就是经历了演绎推理的过程。
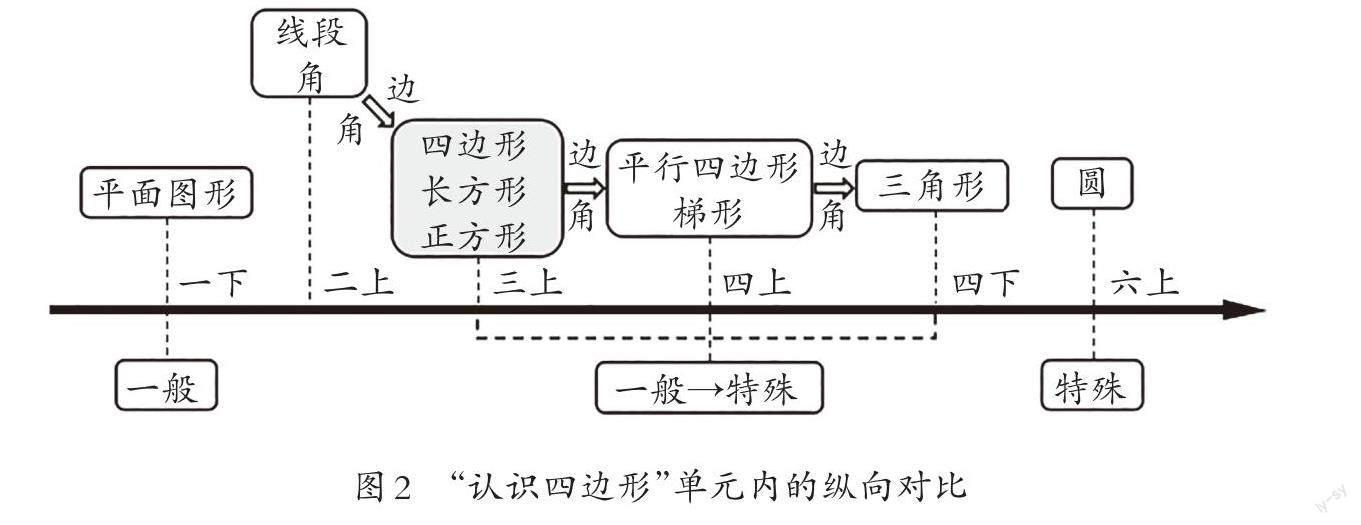
接着,笔者对这一内容进行了纵向对比(见图2),发现“平面图形的认识”这一板块的教学编排上也体现着这样一条思想暗线:三年级本单元的内容是从一般走向特殊,后续的平行四边形、三角形教学也是如此,最后再从“一般”的直边图形走向“特殊”的曲线图形。可见,本课是图形认识领域演绎推理思想的初次渗透,是后续图形关系推理的基础。
再从学习方法来看,掌握四边形、长方形、正方形的特征提炼技巧是本课的重点。实际上,在一年级时,学生已经有了根据外观整体辨认图形的经验,本课则是要帮助学生从表象认知水平进入到依托特征判断的定性分析水平。在二年级时,学生已经有了基于边、角来认识图形的经验,本课以及后续对于平行四边形、梯形、三角形的学习也都可以从这两个要素出发去研究。因而,在教学中凸显“边”和“角”这两个判断图形特征的要素,既能让学生的推理有依据、有方向,也能为后续学习打下基础。
(二)为“诊”而测,把握教学起点
为了更精准地了解学生对于四边形、长方形以及正方形的已有经验,以学定教,笔者抽取了城镇中心小学三年级全体学生(共225人)进行前测。
从学生作答中笔者发现,学生借助点子图画一个任意四边形正确率是较高的。问题在于,多数学生只能画出生活中常见的特殊四边形,可见,学生对于四边形的认知是不全面的。同样,在辨认正向摆放的长方形和正方形时,学生是没有问题的,将长方形和正方形倾斜放置后会对部分学生的判断产生一定的干扰,而那些非常近似长方形或正方形的四边形是学生最容易错选的。这就反映出学生对于这些看似熟悉的图形,有一定的经验生成,但在辨别时缺少理性的判断方法和依据。因此,教学素材的选取以及判断依据的提炼是本课需要关注的点。
基于教材和学情的整体考量可以发现,本课在整个图形认识领域起着承上启下的作用。为此,本课仅止步于知识点的教学是远远不够的,教学中关注知识背后的思想方法也尤为重要。教师挖掘与凸显方法的相似性,紧抓边角,展开由表及里的演绎推理,既能帮助学生走出仅凭直觉判断的前经验,也能让其形成图形关系探究的自主迁移能力。
三、学生立场,强化推理,搭建有效的学习路径
如何让抽象的“演绎推理 ”在学生的脑海中鲜活起来呢?让学生完整地经历演绎推理的过程,是使其领悟并发展推理能力的有效途径。
(一)顺藤摸瓜——拾“证据”基础,孕伏演绎推理
演绎推理是借助逻辑推演获取结论的一种思维方式,需要有一般性“证据”作为推理前提。四边形、长方形、正方形的特征便是本课演绎推理的关键证据。而边和角作为构成平面图形的两个基本要素,能为学生提炼特征、展开推理指明方向,以保证学生能够快速地寻得并列举出符合目标的“证据”。
1.寓学于趣——着眼起点,凸显边角明方向
演绎推理的过程是抽象的,数学知识本身又是枯燥的,因此笔者以“四边形派对”为主情境展开教学,借趣味来支撑学生进行深入的研究(见图3)。
基于经验,学生心中已有了四边形的雏形,只是缺少恰当的激活。本课借助“你心目中的四边形有怎样的特征”这一问题,促进学生新旧知识的衔接,为后续的分类活动提供一定的标准和方向,初步感知研究图形的要素。分类活动则是将学生“原认知”中的误区和难点直接暴露在课堂中,借助辨析帮助学生的思维逐渐聚焦到图形边和角的特点分析上,使“证据”的提炼更具指向性。
2.返璞归真——巧选素材,去除干扰明本质
演绎推理需要学生具有一定的抽象思维能力,让学生经历去除外在非本质要素,明晰内在本质特征的过程,是提升其抽象思维能力,发展辩证眼光的重要途径。合理选取和使用学习素材能有效助推学生寻得图形背后的秘密,习得透过现象看本质的能力。
层次一:多元表征,去“饰”留“形”。
在特征提炼环节,笔者提供了形状、颜色、大小以及摆放方向各不相同的材料供学生观察思考,让学生基于从“边”和“角”出发观察的经验,准确提炼出这些看似不同的长方形、正方形背后存在的共性特征。
层次二:素材整合,求“同”存“异”。
在上述探究活动结束时,笔者将这些素材整理后再次重现在学生眼前(见图4),通过进一步地观察、分析、比较,使学生形成对长方形和正方形更精确化的认识。
观察比较:这些刚才验证过的长方形和正方形,你有什么发现?
追问:为什么正方形形状始终不变,而长方形却有“高、矮、胖、瘦”之分?
本次观察任务,以旧素材、新视野去分析长方形和正方形的特征,让学生进一步认识到影响长方形、正方形形状的仍旧是它们的边和角。即,长方形的形状同时受到长和宽的影响,所以长方形会出现不同的形状;而正方形无论边长是多少,它的四条边始终相等,从而使正方形形状始终不变。上述两个层次的观察任务,由易到难,引领学生逐步深入知识本质,触及长方形和正方形的内在属性。
(二)精准表达——用“证据”说话,外显演绎推理
演绎推理强调推理过程的严谨性,学会用规范的数学语言外显内在的思维逻辑是演绎推理得以发展的关键。简而言之,就是要让学生学会说理,使学生在一次次用缜密的语言表达思维的过程中,深化对演绎推理的认识。
1.“演”:关注过程——从合情走向合理
数学论证的重要形式之一便是演绎推理,借演绎推理验证并阐明“证据”的合理性,能让学生对得来的线索始终保持审慎态度。本环节若直接用语言描述抽象且繁杂的推理过程不利于学生理解与接纳,为此,笔者给学生提供了彩色水笔和若干正方形、长方形卡片,让其在边演示边解说的过程中,清晰地呈现演绎推理的过程。
【片段1】论证正方形的4个角都是直角
生:(大前提)首先,通过对折发现正方形的4个角完全重合,可以得到正方形的4个角相等。(小前提)其次,借助三角尺比照,发现其中一个角是直角。(结论)最后,由此可以得到正方形的4个角都是直角。
【片段2】论证正方形的4条边都相等
生:(大前提)因为通过上下对折可以发现红色的这组对边相等,左右对折可以发现蓝色的这组对边相等。(小前提)又因为沿对角线对折发现红色和蓝色这两条邻边也相等。(结论)所以正方形的4条边都相等。
生:(大前提)第一次沿对角线对折发现红色的这组邻边相等,蓝色的这组邻边相等。(小前提)第二次沿对角线对折发现红色和蓝色这两条邻边也相等。(结论)所以正方形的4条边都相等。
以上学生出现的3种验证方法其实都蕴含着“三段论”形式的演绎推理,即2个前提加1个结论。在说理时,教师应引导学生用“首先,其次,由此”“因为,又因为,所以”等逻辑语言来完整地表述推理过程,感悟三段论推理的模型。
2.“绎”:抽出精髓——从对立走向统一
在演绎推理的过程中,不仅要让学生明确“证据”的可靠性,更应让其关注到“证据”背后的关联,从二元对立的思维中走出来,整体把握图形之间的关系,使部分与整体的关系教学得以突破。
(1)冲突造势,经历简单判断,培育推理的“幼芽”
推理能力的发展不是一蹴而就的,安排由浅入深的推理活动符合学生的认知发展规律。为此,本课先由推理简单的关系入手,借助“形”来引发学生的认知冲突,通过“理”助其走出固有的刻板印象,让演绎自然发生。
【片段3】推论凹四边形是不是四边形
抛问:现在再来看看这个图形(凹四边形),你们的疑问消除了吗?它到底是不是四边形?
生:不是,它只有3个角。
生:不是,它的第4个角在外面。
生:是的,它有4个角和4条直边。
方法引领:看来大家有疑问的就是这个是不是角。其实,从一个点引出两条线,形成一个的大角,它也是角,我们数的是图形里面的角。
小结:四边形有4个角和4条直边,这个图形也有4个角、4条直边,符合四边形的所有特征,所以它也是四边形。
以上3名学生的推理过程实际都是省略形式的演绎推理,推理时把“四边形有4个角和4条直边”这个大家一致认可的大前提隐去了。尽管学生的表述并不属于严谨形式的三段论,但他们的推理过程实际是严密且富有逻辑的。教师可以有意识地完整小结,为其进行更复杂的演绎推理打下坚实基础。
(2)动画助力,目睹复杂转变,舒展辩证的枝叶
直观地展示图形间的关联是破除对立思维、展开深度推理的有效途径。为此,本课改抽象为直观,让4个顶点动起来,呈现由普通凸四边形到长方形,再到长边缩短的长方形,乃至正方形的变化过程。借助这样的动态演示,突破三者关系(见图8):
通过视觉,学生能够直观地看到“邊带动角”“角带动边”的过程,初步感知三个图形的关联。此时,借助问题“长方形是不是四边形”“正方形是不是长方形”,引发他们的思辨,在演绎推理中引领学生的思维从直观过渡到抽象:因为四边形有4条直边和4个角,长方形也有4条直边和4个角,所以长方形是四边形;因为长方形的4个角都是直角且两组对边相等,正方形也有4个直角且对边相等,所以正方形是长方形。每一次说清楚推理依据与结论的过程,都能加深学生对这三者本质的认识,助其搭建起关系结构,形成“对立统一”的辩证思维。
(三)见微知著——扩“证据”体系,伸展演绎推理
演绎推理的价值不仅仅在于得到一个科学的结论,还在于使学生掌握这种学习方法,并使其成为一种思维能力。恰当的沟通与联系,是凸显不同事物之间相似性,使思想方法得以迁移的重要手段。
借力点1:课中串联 ,明“证据”提炼方法
提问:这些留下来的四边形中,有你熟悉的“老朋友”吗?
生:有,梯形、长方形、正方形、菱形、平行四边形。
师:其实,这些有特殊名称的四边形,除了有4个角和4条直边外,还有各自的特点,我们仍然可以从角和边入手对它们进行更深入的研究。
借力点2:收尾延伸,显“关系”推理要领
总结引领:以后我们还会学习前面提到的平行四边形、菱形和梯形,在研究它们时同样可以从边、角入手去观察。这些图形与我们今天学过的图形可能也存在着密不可分的关系,同样可以基于关联视角去推理验证。
平面图形的特征提炼过程存在相似性,甚至图形关系的推理过程也存在相似性,借助语言外显图形内在的联系,能为新知识与新结论的获取指明方向和思路,能让学生的思维完成从此类到彼类的跨越,进而让演绎推理的迁移有迹可循。
教师在日常教学中应不断挖掘教材背后的演绎推理,帮助学生养成抽象辩证的“数学眼光”,形成注重逻辑的“数学语言”,达成严谨审慎的“数学思维”,让数学核心素养真正落地。
参考文献:
[1]成婕妤. 小学生数学演绎推理能力发展研究[D].上海:上海师范大学,2022.
[2]祁倩倩. 立足实践操作,发展演绎推理能力:以“证明”的教学为例[J]. 数学教学通讯,2023(5).
(责任编辑:杨强)
