一类小车倒立摆的起摆稳摆时滞控制研究*

冯欣炜 胥奇† 杨正兵 李映辉

(1.西南交通大学 力学与航空航天学院,成都 610031) (2.中国航发 四川燃气涡轮研究院,成都 610500)

引言

倒立摆系统结构简单,同时又具有强耦合、强非线性和开环不稳定等特点,是控制理论和实验研究的理想平台.含倒立摆原理的系统十分常见,以四轴飞行器为例,孔凡国等[1]将该飞行器从三维空间简化为二维平面内的倒立摆模型,从而降低了研究难度.火箭在上升阶段对俯仰角的控制也可以抽象为传统倒立摆的稳定控制[2,3]:Gomez等人[2]用含复杂气动力的倒立摆模型对无尾翼火箭进行建模,并提出了其主动导航策略;罗轶欣等[3]根据倒立摆模型搭建了三维火箭稳定控制平台.Tanaka等[4]将轮式机器人简化为轮式倒立摆模型,并在简化后倒立摆模型的顶部安装控制力矩陀螺,进一步研究机器人的姿态稳定控制.以上这些实例均为含倒立摆原理的模型,将这些模型简化为倒立摆系统后更便于检验控制律、优化分析等.

小车倒立摆系统通过小车控制倒立摆的运动,其控制方式主要包括起摆控制和稳摆控制两种[5].起摆控制通常使用基于能量的控制律[6],即通过对摆杆的能量控制来起摆.但纯能量控制策略可能导致小车位移过大,因此需进一步优化,比如:通过引入小车位移极限来满足系统对小车位移的限制[7];利用自激原理改进的能量法[8]能够快速积蓄动能,不仅能在极少的摆动周期内实现摆起,还能用力矩很小的电机完成大负载倒立摆系统的摆起.稳摆控制可以使用经典的PID控制或最优二次型控制等等.针对PID控制使用试凑法调试参数的缺点,可通过遗传算法等来整定PID参数[9],进而优化控制效果.

在工程领域的主动控制技术中不可避免地存在时滞现象,例如信号经过低通滤波器后存在延时,这种特性称为滤波器的群时延[10].为了减少时滞对控制的影响,需要将时滞引入控制律中进行考虑.刘建均等[11]在汽车悬架系统中引入时滞加速度反馈控制,通过粒子群优化算法得到了不同路面激励频率下的最优时滞,以改善汽车的隔振性能.姚远等[12]在研究列车转向架控制系统的稳定性时也考虑了时滞的影响,发现列车在高速运行情况下,在一定范围内增加时滞可提高系统稳定性,但较大时滞导致系统失稳,文章同时提出了一种反馈附加振子的方法来减小时滞的影响.在针对轮式倒立摆的稳摆运动研究中,若以单个加速度计为传感器,则时滞P控制和时滞PD控制都无法使得系统稳定,但通过附加阻尼装置,稳摆运动在包含控制时滞的情况下得到控制[13].在实践中,实际控制器的时滞量可能会存在波动变化.比如,由于传感器的采样时间和时滞是时变的,Fritjof等[14]设计了一种测量系统偏差更新方法,使得在时滞和采样时间是时变的情况下仍可以提供稳定的过程估计,但该方法仅在时滞小于或等于采样时间时才成立.陈晓昊[15]在研究磁浮系统的时滞控制时,考虑真实条件下时滞不是定值,并通过试验得知了时滞大小在0.015～0.020s之间,据此研究了控制器波动时滞对磁浮系统稳定性的影响.赵远征[16]研究了车载伺服系统时滞波动τ±30时控制器的效果变化,并发现分数阶PD控制器相比整数阶PID控制器有更强的鲁棒性.Insperger[17]研究了车削过程状态相关时滞模型的非线性动力学特性,该模型考虑的时滞与系统状态,不仅取决于工件的旋转,还受到刀具振动的影响.Stepan等将零阶保持的数字控制系统等效为具有时变时滞的连续系统,进而使用半离散化方法对系统的稳定性和非线性动力学进行研究[18,19].Lyapunov稳定性判据也被用于处理时变时滞系统的稳定性问题,比如自由权方法[20],转化为区间时变时滞法系统进行研究[21],等等,这些工作相当一部分致力于降低结果的保守性.综上可见,考虑控制系统中的时滞是有必要的,不仅可以厘清时滞的不利影响,还可能利用时滞,实现更好的控制效果,进行相关研究.

小车倒立摆从起摆控制到稳摆控制的过程,涉及控制律的切换.切换系统是由一系列的连续或离散的子系统以及协调这些子系统之间的切换规则组成的混合系统.切换时滞系统是结合时滞和切换信号提出的一种特殊的切换系统,其模型比一般切换系统更加复杂[22].共同Lyapunov泛函方法[23]是早期学者研究切换时滞系统在切换信号下是否稳定的方法,所有子系统共享一个公共的Lyapunov泛函,但没有考虑各个子系统的特殊性是它的局限;后续的切换Lyapunov泛函方法则考虑了每个子系统的特殊性,Daafouz等[24,25]就利用切换Lyapunov泛函方法及相关理论研究了切换系统的稳定性与控制问题.李志成[26]用一种模型转化方法,将切换时滞系统转化成首尾相连的输入输出系统,通过新的Lyapunov函数辅助输入输出方法,研究切换时滞系统的稳定性,其还利用输入输出方法研究了具有部分转移概率已知的时变时滞马尔科夫跳变系统的稳定性分析[27].Sun等[28]研究了切换时滞系统的稳定性分析和增益分析问题.Zhang等[29]讨论了离散切换时滞系统的稳定性分析问题.值得注意的是,当前针对切换时滞系统的研究中,主要集中于探究系统的稳定性,而鲜有关于瞬态时域性能的研究工作.在小车倒立摆的控制中,小车的摆幅大小是典型的瞬态响应.过大的小车摆幅受限于系统空间限制可能难以实现,同时也会消耗过多的控制能量.因此,研究小车倒立摆的起摆和稳摆的切换控制,也应该关注时滞对于瞬态时域性能的影响.

本文以一级小车倒立摆系统为研究对象,使用时滞能量起摆控制和时滞串级PD控制分别对系统进行起摆和稳摆控制,同时研究了两种控制在切换过程中时滞的影响.本文所研究控制器中均为常时滞,并不考虑控制器中时滞量的波动变化.在研究过程中,提出了一种简化方法,以分析时滞对系统稳定性以及瞬态时域性能的影响;同时,将时滞作为优化参数,发现考虑系统时滞的控制律,可以实现比无时滞控制更好的控制效果.本文的研究成果可为类似系统的时滞控制研究提供理论参考.

1 系统的切换控制模型

1.1 系统模型

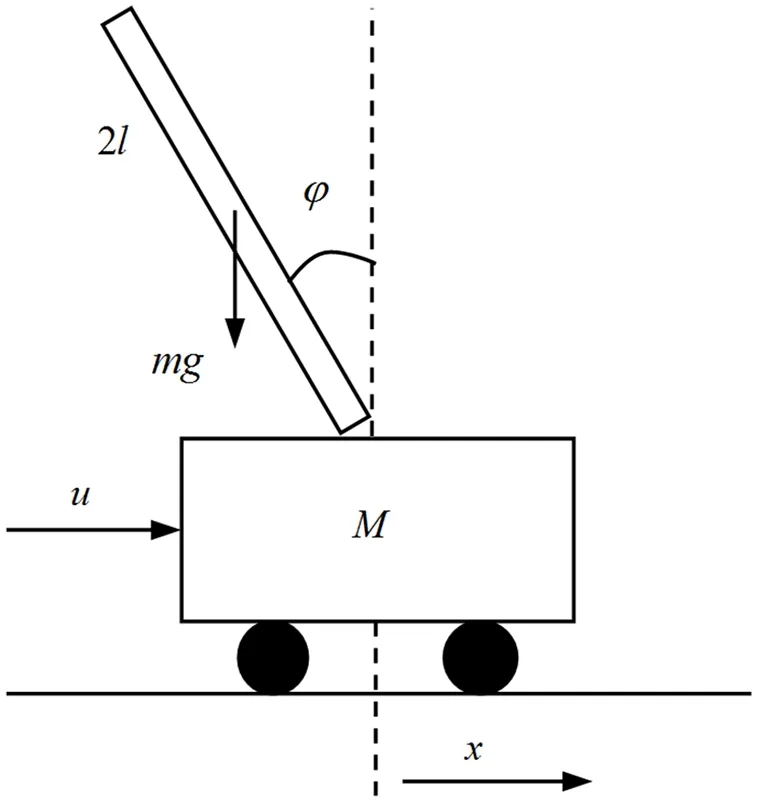
图1 小车倒立摆系统的模型示意图Fig.1 Model diagram of trolley inverted pendulum system

倒立摆的系统模型如图1所示,其结构参数等由表1给出.由Lagrange方程法[30],可以得到系统的动力学模型为:

(1a)

(1b)

其中x为小车位移、φ为摆杆与竖直向上方向的夹角角度,u为控制力.

初始状态下,倒立摆位于垂直向下的角度,即φ=-π.本文通过控制力u控制小车的运动,先使用起摆控制律将倒立摆摆起,再切换至稳摆控制律,使倒立摆稳定在垂直向上的角度.整个控制过程应当尽可能使小车位移小、稳摆时间短.

表1 小车倒立摆系统的参数设置

1.2 起摆控制

我们考虑含时滞的能量控制律来进行起摆控制,参考文献[31]中的控制律,其中控制律的能量描述主要是基于摆杆的机械能.

设摆杆在自然下垂的状态下重力势能为-2mgl,在摆杆竖直向上稳定时重力势能为0.摆杆在转动时,机械能为

(2)

考虑到轨道长度的限制,小车的速度最终应收敛到零.将Lyapunov函数设置为

(3)

(4)

并根据式(1b),可得

(5)

本文直接根据文献[32]构造控制律:

(6)

本文考虑状态变量具有时滞,对式(6)进行处理,最终得到时滞起摆控制律为:

(7)

其中k、α、β、η均为可调参数,且α、β的量纲分别为ML2、ML2T-2,本文中取α=0.0042、β=0.49,将k和η作为主要控制参数.

1.3 稳摆控制

当倒立摆摆起到一定角度后,控制律切换为稳摆控制律.在稳摆阶段,摆杆晃动幅度较小,可以使用线性控制方法.在此平衡点φ=0处对系统方程(1a)、(1b)进行线性化处理,可得:

(8)

后续使用时滞串级PD控制来对摆杆角度和小车位移进行控制,控制流程如下图:

图2 串级PD控制示意图Fig.2 Schematic diagram of cascade PD control

其中Φ(s)、X(s)、U(s)分别为φ、x、u的拉氏变换.

在该控制下,系统所受控制力即:

(9)

式(9)中Kp1、Kd1、Kp2、Kd2为分别为角度、角速度、小车位置、小车速度偏差增益.

在串级PD控制中引入时滞τ,可得时滞串级PD控制:

(10)

2 起摆时滞的影响分析

本节探究时滞对起摆控制时系统能量的影响.我们研究摆杆一个周期内的运动状态的变化.其中,摆杆运动的一个周期定义为,摆杆从竖直向下且负方向摆动开始,并再次回到竖直方向且角速度方向同样为负的状态.探究此时时滞的影响.

Lyapunov函数(3)主要与能量有关,本文从该函数入手,并研究Lyapunov函数的时间导数(5).起摆控制律依据式(5)括号内的式子,类似于起摆控制中引入时滞,在式(5)括号内式子中也引入时滞,可以得到

(11)

式(11)是一个复杂的非线性方程,难以进行有效分析.为简化分析,我们对系统每次由负方向运动至φ=-π时的情况进行分析.此时有φ(t)=-π,由于时滞很小,也近似认为φ(t-τ)=-π.同时,考虑时滞很小,对式(11)做关于时滞的一阶泰勒展开.可得

(12)

其中

(13)

对于无时滞系统,有A<0,当时滞很小时,可以得到:(a)若B>0,则引入时滞会令式(12)的系统的能量变化变慢;(b)若B<0,则引入时滞会令式(12)的系统的能量变化变快.需要注意的是,以时滞为小量进行泰勒展开,需要考虑研究问题的特性,比如将时滞微分方程泰勒展开为常微分方程以进行稳定性分析,往往是不可取的.同时,上式分析的是摆杆竖直向下时刻的能量变化速度,该规律是否适用于整个周期的运动,我们可以使用数值方法进行验证,或者多选取一些特殊位置进行类似分析.

(14)

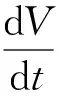
(15)

可见此时时滞的效果与第一个周期时相同.

(16)

(17)

图3给出了前几个周期内系统Lyapunov函数(3)的结果.可以发现,在前两个周期,带有时滞系统的能量明显比无时滞系统的能量变化地慢.再研究前几个周期内经处理的Lyapunov函数导数(12)的变化,此时只利用无时滞系统的仿真数据,将三种时滞代入式(12)中,结果于图4可见.图4中在2.5s后虽有部分数值会大于0,但此时摆杆已基本摆起,可以顺利切换到稳摆控制,因此可以认为起摆控制律总体上是有效的.在3s之前,图4主要有三个峰值,后两个峰值处含时滞系统的能量变化速度(幅值)要明显小于无时滞系统的能量变化速度.这使得时滞系统的摆杆到达切换控制处时,角速度会比无时滞情况下要小,进而令后续的稳摆控制也能更快稳定.但在时滞较大时,起摆过程中摆杆则会出现明显的滞后,所以要选择合适的时滞来优化起摆.

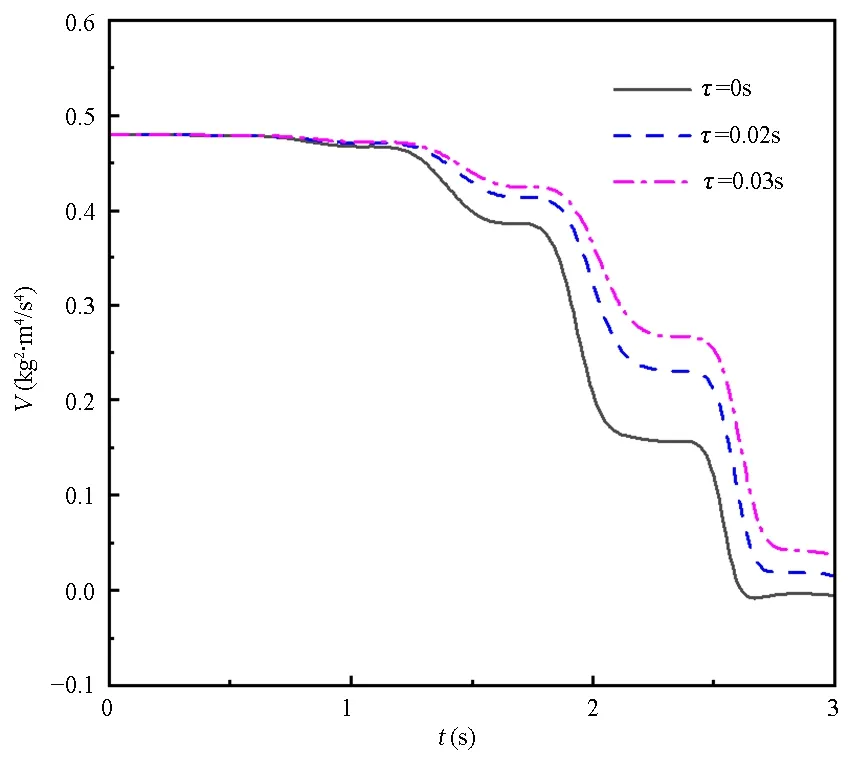
图3 不同时滞下的Lyapunov函数Fig.3 Lyapunov function with different time delays

图4 不同时滞下的Lyapunov函数的导数Fig.4 Derivative of Lyapunov function with different time delays

3 稳摆时滞的影响分析

3.1 系统特征函数

稳摆过程摆杆晃动角度较小,因此可以使用线性方法,通过分析受控系统的最大实部特征根的位置,来讨论控制效果.将控制律(10)代入式(8),并进行拉普拉斯变换,可得

(M+m)X(s)s2+bX(s)s-mlΦ(s)s2=

-Kp1Φ(s)e-sτ-Kd1Φ(s)se-sτ-Kp2X(s)e-sτ-

Kd2X(s)se-sτ(I+ml2)Φ(s)s2-mglΦ(s)=

mlX(s)s2

(18)

由式(18)可得:

(19)

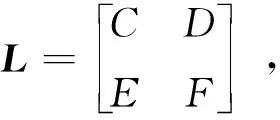
(20)

将式(20)中的替换为λ,并由|L|=0,可得系统的特征方程

f(λ;τ):=[(M+m)(I+ml2)-m2l2]λ4+

[(I+ml2)(b+Kd2e-λτ)+Kd1mle-λτ]λ3+

[Kp1mle-λτ+(I+ml2)Kp2e-λτ-(M+m)mgl]λ2+

[-mgl(Kd2e-λτ+b)]λ-mglKp2e-λτ=0

(21)

3.2 特征根计算

为研究时滞对于特征根λ(τ)的影响,我们采用数值算法[32],通过隐式微分求解由f(λ;τ)=0得到的非线性常微分方程来得到λ(τ).该方程如下:

(22)

通过代入不同的初始条件λ(0),可以得到满足f(λ;τ)=0的不同解支的λ(τ).

对于线性时滞系统而言,其特征根解支有无穷个,此处我们列出对系统响应影响最大(即特征根实部最大)的两个解支,如下图5所示.这两个解支可由特征方程的特征根-0.2068±1.3467i和-11.7423±9.3977i为初始条件得到.系统其他的特征根实部均非常小,对系统响应的影响也很小,因此可以忽略.

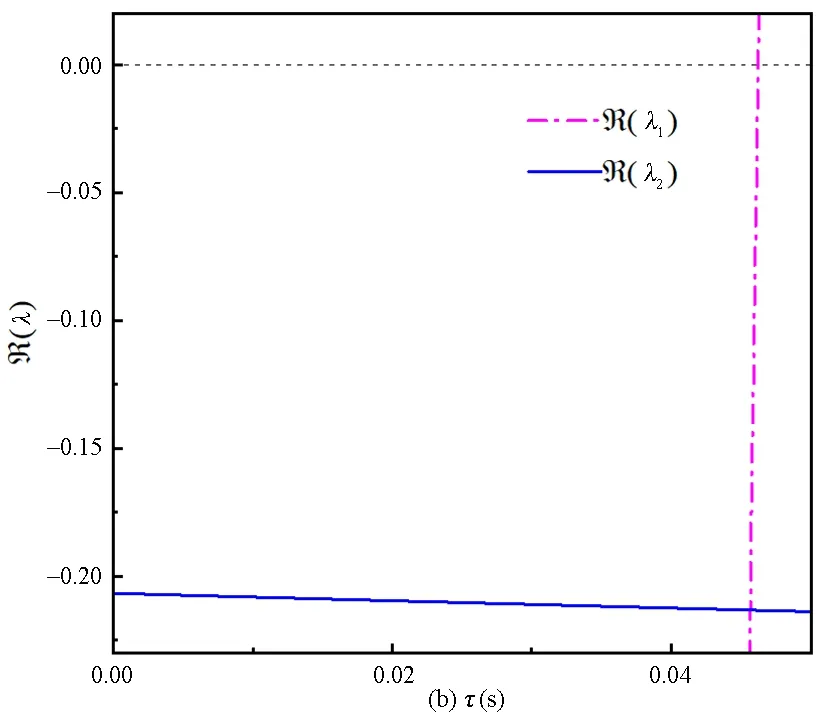
图5 特征根实部与时滞关系图(为便于观察最大实部特征根,图(b)为图(a)中纵轴靠近零处的放大)Fig.5 The relationship between real part of characteristic root and time delay (For the convenience of observing the maximum real part of characteristic root, Fig (b) shows the magnification of the vertical axis near zero in Fig(a))

计算结果于图5可见,特征根λ1的实部在区间[0,0.05s]内,随着时滞的变大先变小再变大,最终在τ=0.0462s处越过坐标轴;特征根λ2的实部变化不大,并且始终没有越过坐标轴.于是可以得到时滞稳定区间为[0,0.0462s].进一步地,由于最大实部特征根的实部在[0,0.045s]内一直减小,甚至在时滞区间[0,0.021s]内两对根的实部均在变小,我们可以得出结论:系统在小时滞情况下,有时滞控制相较于无时滞控制效果理论上应该更好.不过由于最大实部特征根的实部变小的程度较低,实际上有时滞控制相较于无时滞控制,在收敛速度上的区别并不明显.从最优的角度来说,根据文中图5(b),系统的稳摆时滞约0.045s时,最大实部特征根实部为负,且绝对值最大,故可以认为此时系统稳定性最好,且摆角收敛最快;但考虑到系统鲁棒性,若时滞值超过0.0462s,系统将会失稳,控制律会失效,因此0.045s的时滞从鲁棒性角度来说不是较好选择,实际时滞应该取小于0.04s更为适宜.

后续用定积分判别法[33,34]来验证其时滞稳定区间.定积分判别法由辐角原理发展而来,计算相对简便,且适用于含多个离散时滞的中立型或滞后型时滞微分方程的稳定性分析.首先计算系统的特征函数f(λ;τ),利用式

(23)

将特征函数f(λ;τ)代入式(23)中,积分上限T取200(积分上限的临界值可参考文献[34]);R(·)为实部,n为特征函数最高次数,对于该系统n=4,为取整函数.代入时滞进行计算,计算结果若,则系统渐近稳定;若N>0,系统不稳定.将相关的参数代入式(23)中,通过计算,可得到不稳定根个数与时滞的关系,于图6可见.

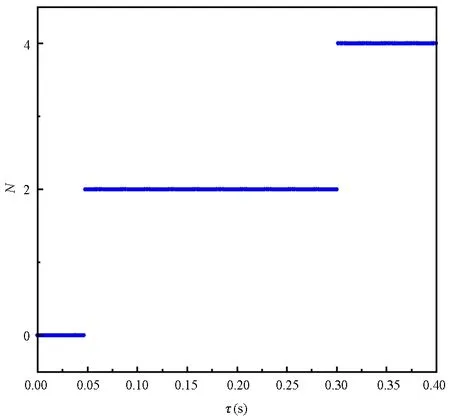
图6 不稳定根个数与时滞的关系图Fig.6 Diagram of the relationship between the number of unstable rootsand the time delay

系统特征方程的解的不稳定根个数为零时,此时系统为渐近稳定,即图6的N=0的部分,在该时滞范围之内,系统渐近稳定.取N=0时最右端的点,可以得到该点的坐标为(0.046,0).因此,在时滞范围[0,0.046s]内,该系统能够渐近稳定.与图5得到的时滞稳定区间[0,0.0462s]可以相验证.

4 时滞的综合影响

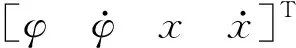
(24)

(25)

仿真结果见图7到图10.

由图7到图10可知,三种时滞都可以使得系统实现起摆到稳摆的控制,但是控制过程中系统的瞬态响应有较大区别,尤其是小车的运动范围在稳摆阶段的差异尤其明显.进一步地,三种时滞情况下摆杆到达平衡位置的时间以及摆杆的角速度相差无几,但在τ=0.02s、τ=0.03s的情况下,稳摆阶段小车的运动范围以及速度幅值均要比零时滞时更小,且τ=0.03s时小车的运动范围最小.由前面的分析可知,虽然稳摆阶段小车运动范围差异最大,但其原因实质是因为时滞对起摆阶段的影响不同,使得切换后,稳摆阶段摆杆的初始角速度在有时滞时,比无时滞情况下要小.因此,综合两阶段时滞对摆杆和小车的影响,我们认为对于该系统,选取τ=0.03s可有效达到优化控制效果的作用.考虑到实践中控制器已存在一定的时滞,若该时滞比需要的时滞τ=0.03s还低,则可以通过在控制律中人为引入时滞来改善控制效果;若控制器里时滞比需要的时滞τ=0.03s高,则需要通过改善硬件、时滞补偿等方法来降低时滞.

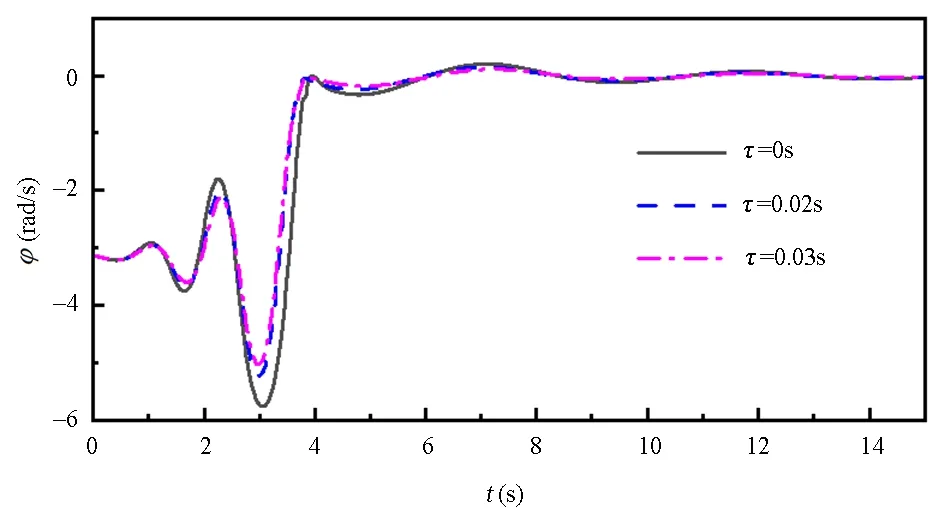
图7 倒立摆角度与时间关系Fig.7 Relationship between angle of pendulum and time

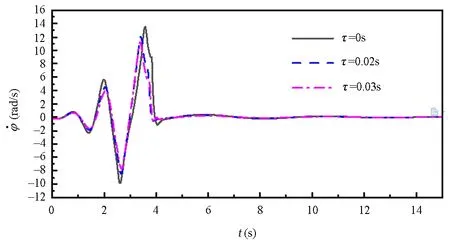
图8 倒立摆角速度与时间关系图Fig.8 Relationship between angular velocity of pendulum and time

图9 小车位移与时间关系图Fig.9 Relationship between displacement of trolley and time

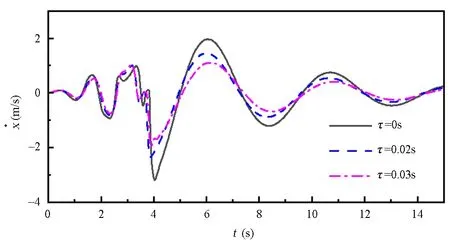
图10 小车速度与时间关系图Fig.10 Relationship between speed of trolley and time

另外,本文尚未综合考虑起摆稳摆控制下的时滞最优解问题,由于起摆控制和稳摆控制的优化目标不同,故稳摆控制的最优时滞也并非最优的起摆时滞.综合控制下的最优时滞,需要根据优化目标确定各指标的权重,并结合多参数最优方法进行分析.本文在满足一定鲁棒性的基础上,在0,0.02s,0.03s三种工况中选取了时滞影响较好的情况,而对于最优时滞还有待进一步研究.

5 结论

本文对一级小车倒立摆进行起摆和稳摆控制,并研究了时滞控制效果的影响,包括系统的瞬态时域特性和稳定性.其中,提出了一种简化方法,使用线性时滞表达式,对特定运动时刻的Lyapunov函数导数进行近似,证明了时滞可以优化非线性起摆控制阶段的能量输入;同时使用定积分法分析了稳摆的稳定性.研究表明,在小时滞的情况下,由于时滞能有效减小系统摆杆在切换时刻的动能,增大时滞使得小车的往返运动幅值也会明显变小.在稳摆阶段,随时滞增大,系统的稳定性先是增强,而后减弱直至失稳.因此,对于小车倒立摆系统引入适当的时滞控制,可以同时实现优化瞬态时域特性和稳定性的效果.