单向耦合FitzHugh-Nagumo神经元的滞后同步研究*
2023-11-18袁韦欣镇斌徐鉴
袁韦欣 镇斌† 徐鉴
(1.上海理工大学环境与建筑学院,上海 200093)(2.同济大学航空航天与力学学院,上海 200092)
引言
耦合神经元之间的同步现象一直是脑科学、医学、人工智能等领域学者持续关注的热点.单个神经元细胞并不具有智能表现,神经元之间的同步则与大脑的认知和行为具有相关性[1-4],而进一步通过研究神经元之间的同步来理解大脑中的信息处理也被证实是可行的[5-9].Hodgkin-Huxley(HH)方程[10]以及它的简化版:FitzHugh-Nagumo(FHN)模型[11],Hindmarsh-Rose(HR)模型[12]常用于从神经动力学研究的层面上构建神经网络.尤其是FHN模型,其方程形式简单,更适于从非线性动力学的角度研究神经元之间的同步行为.需要注意的是,神经元之间的信息传递并非瞬时完成,通过突触传递的神经信号都会存在不同程度的滞后现象,在某些情况下这种滞后量甚至可以达到系统发放周期的量级[13].因此,在讨论耦合神经元同步行为时,信号传递的时滞因素影响不能轻易忽视.
一般而言,当一个神经元向另一个神经元发送信号时,两个神经元如果在某些特定条件下保持一致就意味着这两个神经元处于同步状态.目前已经发现神经元之间可以存在多种同步状态,如完全同步(complete synchronization)、滞后同步(lag synchronization),广义同步(generalized synchronization)等[14,15].在以往的FHN神经元系统同步研究中,上述几种同步通常被单独加以讨论.对于完全同步和滞后同步,通常采用Lyapunov函数方法[16-18]来获取神经元的同步发生条件.而对于广义同步,则常采用构造辅助系统[19]方法来寻找同步条件.事实上,广义同步更具有一般性,完全同步和滞后同步都可以看作是一种特殊的广义同步.将滞后同步视为广义同步加以研究可能是一种新的研究思路.
本文讨论单向耦合的FHN神经元之间的滞后同步.不同于以往研究,本文将滞后同步视为一种特殊的广义同步,采用构造辅助系统的方法来讨论耦合神经元滞后同步的发生条件.首先,基于拉普拉斯变换,将辅助系统和响应系统之间的误差系统转化为Volterra积分方程.再根据Volterra积分方程理论中的逐次逼近方法(successive approximation method)[20]解析地得到了两个单向耦合FHN神经元的滞后同步发生条件.最后,通过数值模拟验证了本文解析判据的有效性.
1 FHN神经元模型
本文采用的FHN神经元模型如下[11]:
(1)
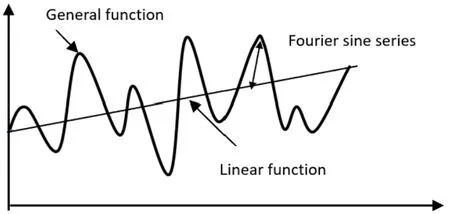
其中w分别表示膜电位和恢复量.a>0,0 (2) α1[u3-u1(t-τ)] (3) 其中α1、2是耦合强度,τ>0表示从u1(u2)到u3(u4)的信号传输延迟.如果在系统(3)中满足 (4) 则两个FHN神经元之间存在滞后同步. F1(t,τ)=u1(t-τ) F2(t,τ)=u2(t-τ) (5) F1,2可以由系统(3)确定.任何函数都可以在有限区间上表示为叠加在直线上的傅里叶正弦级数,如图1所示[21].所以函数可以近似表示为: F1(t,τ)=p0(t)+p1(t)τ+ F2(t,τ)=q0(t)+q1(t)τ+ (6) 图1 在有限区间上,任意函数=线性函数+傅里叶正弦级数Fig.1 On a finite interval, an arbitrary function=a linear function + a Fourier sine series 其中N根据精度需要确定.显然, u1≡F1(t,0)=p0(t) u2≡F2(t,0)=q0(t) (7) 因此,系统(3)中的滞后同步可以被视为一种特殊的广义同步,即: (8) 基于辅助系统方法[19],系统(3)的辅助系统定义如下: α1[u5-u1(t-τ)] (9) 广义同步关系(8)可以在系统(3)中实现,只要如下关系成立: (10) 令 根据系统(3)和(9),e1,2,3,4的控制方程可以写成: (11) 其中 条件(10)等效为 (12) 考虑如下拉普拉斯变换: (13) 对系统(11)中等式两边取拉普拉斯变换,有 (14) 其中,ei0,i=1,2,3,4是系统(11)中给定的初值.另外 求解系统(14)中的前两个方程,有 (15) 其中 ξ1=bγ-d-α1-α2 ξ2=[1-b(d+α1)]γ+α2(d+α1) ξ3=bγ-α2 ξ4=-d-α1 对(15)中的等式两端取拉普拉斯逆变换,利用卷积定理,有 (16) 其中 s1,s2是方程s2+ξ1s+ξ2=0的两个根.显然,η1,2,3→0是条件(12)成立的必要条件.根据Routh-Hurwitz判据,要保证η1,2,3→0成立应满足: ξ1>0,ξ2>0 (17) 在上述条件下,当公式(16)变为 (18) 方程(18)是一个Volterra积分方程,可使用逐次逼近法[20]求解.根据该方法,e1,2=0分别是(18)中两个方程的唯一解.这意味着当条件(17)满足的时候滞后同步会在系统(3)中发生. 对系统(3)和(9)进行数值模拟验证条件(17)的有效性.取a=0.6,b=0.7,γ=0.03,Iext=0.6和α1=-0.8.根据条件(17),系统(3)中会出现滞后同步,只要下列关系成立 α2 α2<[b(d+α1)-1]γ/(d+α1)=0.6004 注意到条件(17)不包含τ,这意味着对任意时滞量同步条件α2<0.0728都有效.在系统(3)和(9)中取初始条件,u1(t)=0.1,u2(t)=0.2,t∈(-τ,0],(u3(0),u4(0))=(0.12,0.21),(u5(0),u6(0))=(0.15,0.22).图2中给出了不同α2和τ值时响应系统和辅助系统之间的同步误差e1=u3-u5,e2=u2-u4的变化趋势,以及u1,3和u2,4的时程图. 图2 系统(3)和(9)中不同α2和τ值时同步误差e1,e2的趋势变化图,及u1,3和u2,4的时程图,其中(a)α2=0.08,τ=0(b) α2=0.02,τ=0 (c) α2=0.02,τ=5 (d) α2=0.02,τ=20Fig.2 Synchronization errors e1,e2 and functional relations between u1 and u3, and between u2 and u4 in systems (3) and (9) with (a)α2=0.08,τ=0(b)α2=0.02,τ=0(c)α2=0.02,τ=5(d)α2=0.02,τ=20 由图2可知,条件(17)与数值结果非常吻合,由此证明了条件(17)的有效性. 本文研究了两个单向耦合FHN神经元的滞后同步问题.与以往采用的方法不同,本文将神经元之间的滞后同步视为一种特殊的广义同步,令构造出的辅助系统与响应系统完全同步来获得原系统的滞后同步条件.通过拉普拉斯变换方法可以将辅助系统与响应系统之间的误差系统由微分方程表示转化为Volterra积分方程表示,再利用积分方程理论中的逐次逼近方法得到误差系统原点稳定的解析条件.该解析条件与滞后同步中的滞后量大小无关,直接数值模拟验证了本文同步判据的有效性.本文为研究神经元的滞后同步提供了一种新的思路.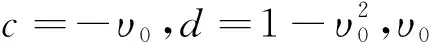
2 广义同步观点下的滞后同步
3 基于辅助系统方法的同步条件研究
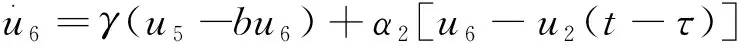
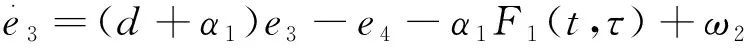
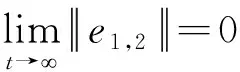


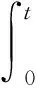
4 数值验证

5 结论
