转子-电磁轴承非线性系统时滞减振研究*

张国荣 王希奎 邹瀚森 张勇 席光

(西安交通大学 能源与动力工程学院, 西安 710049)

引言

旋转机械是工业生产中最重要的设备之一,在大部分工业系统中都发挥基础性的作用,其工作性能的好坏直接关系到整个系统的效率高低.主动电磁轴承因其优良的特性如:转子与定子不接触、可施加主动控制等越来越多地被应用于旋转轴的支撑中.但电磁轴承具有开环不稳定性,需要对其进行闭环控制,并且控制方法很大程度上决定了电磁轴承的工作性能.很多先进的控制方法已被应用到电磁轴承系统中,如滑模控制、H∞鲁棒控制、模糊控制、神经网络等.上述方法相对于传统的PID控制来说具有更好的控制性能及减振效果,但也存在控制器阶数较高、物理意义不明显等短板,因此还未在实际电磁轴承系统中广泛应用.

近年来,时滞控制越来越多的被用于减振.时滞存在于各类控制系统中,在信号的采集、输送以及处理过程中不可避免地会产生一定的时滞[1].系统中时滞的存在可能会使系统性能变差[2], Ji等[3]理论分析了转子-电磁轴承系统的主共振情况,并分析了时滞对稳定性的影响,发现随着时滞量的增加,系统振动幅值增大,稳定解会通过Hopf分岔失稳.近年来,研究人员发现当时滞量取某些值时能对系统的振动起抑制作用.时滞控制就是通过在控制器中添加主动时滞以达到系统减振的效果.Saeed等[4-6]利用时滞饱和控制器去控制梁和转子的振动,发现当时滞量取某些值时,系统的振动被抑制.刘显波[7]利用时滞状态反馈改进了PID控制器去控制纵扭耦合的钻柱系统,发现改进后的控制器使系统稳定域扩大.Amer等[8-9]利用时滞反馈控制器成功减小了Duffing振子和Rayleigh-van der Pol-Duffing 振子的振动幅值.赵艳影等[10]研究了时滞非线性动力吸振器的减振作用,发现当参数都调整合适时,系统振动较无时滞可减小90%左右.为推进时滞反馈控制的实际应用,Yan等[11]设计了实验平台去研究车辆支撑系统中考虑时滞的最优控制规律,研究结果表明合适的时滞量会降低系统幅值,但时滞量与振动幅值之间为高度非线性关系.邵素娟等[12]利用时滞减振技术成功减小了车辆主动悬架系统的振动,其运用多尺度法建立了系统的非线性模型,并研究了系统参数对系统稳定性的影响.

以上展示了近年来研究人员对于时滞控制的研究进展,但在高速转子-电磁轴承系统中时滞对系统的影响以及减振研究报道还较少.因此,本文主要研究时滞反馈控制在转子-电磁轴承系统中的应用.首先建立了时滞状态反馈的转子振动方程;其次利用多尺度法推导出转子在主共振情况下振动方程的近似解并进行稳定性判定;然后详细分析了不同时滞量对振动幅值和稳定性的影响,研究了控制参数对时滞“减振区域”的影响,以及在不同转速、不同质量偏心率下时滞减振的效果;最后通过数值计算验证了近似解的准确性.

1 建立模型

图1为转子-电磁轴承闭环系统示意图.电涡流传感器获得转子位移;控制器根据转子位移计算出相应控制电压;功率放大器根据控制电压的大小产生相应的控制电流Ic.系统采用差动驱动模式,即一个磁铁由偏置电流I0与控制电流Ic的和驱动,另一个磁铁由两者之差驱动,由此产生电磁力对转子进行主动控制.

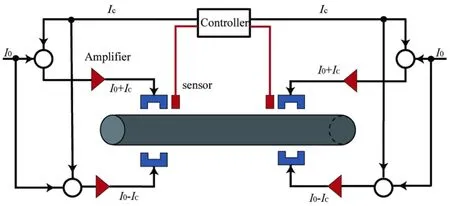
图1 转子-电磁轴承系统示意图Fig.1 Schematic diagram of rotor-active magnetic bearing system

1.1 方程推导

图2为转子-八极电磁轴承系统的截面图.转子为刚性转子模型,忽略磁泄露、涡流效应等对本文研究目标影响较小的因素.

第j(j=1,2,3,4)个磁极对的电磁力[13]为

j=1,2,3,4

(1)

其中,μ0为真空磁导率,Aα是磁极的横截面积,N是线圈匝数,I0代表偏置电流,Ij是第j个磁极对的控制电流,C0是磁极与转子的额定间隙,wj是第j个方向的转子位移,θ代表电磁力作用在转子上的角度.

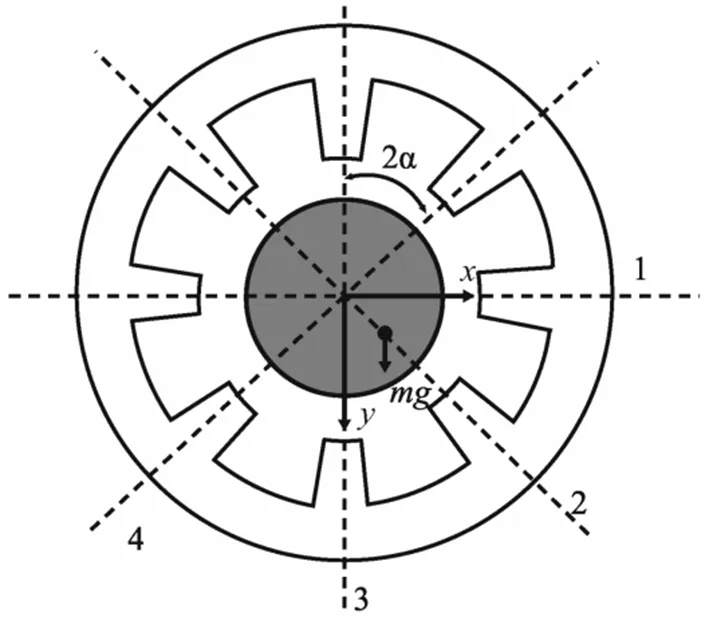
图2 转子-八极电磁轴承系统截面图Fig.2 Sectional view of rotor-eight pole legs magnetic bearing system

采用时滞状态反馈的PD控制,有

(2)

其中,τ1为位移信号总时滞,τ2为速度信号总时滞,kp为位移增益,kd为速度增益.

图2中磁极与磁极之间夹角2α=π/4,因此转子在第j个磁极对方向的位移与相应控制电流为

w1=x,I1=i1,

w3=y,I3=i0+i3,

(3)

x,y方向电磁力合力为

(4)

其中,Fj(j=1,2,3,4)代表图2中j方向磁极对的电磁力.将(1)～(3)带入(4)可得到电磁力的具体形式.

转子在x和y方向上振动方程为

(5)

其中m、c、e、Ω、g分别为转子质量、转子阻尼系数、质量偏心率、转速、重力加速度,Fx为水平方向电磁力合力,Fy为竖直方向电磁力合力.

引入下列无量纲量

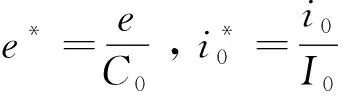
(6)

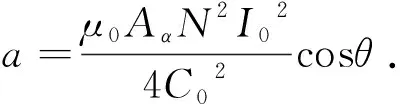
当转子稳定在中心即y=0时,y方向电磁力合力应与重力平衡[13],故有

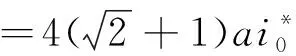
(7)

将式(4),式(6),式(7)带入式(5),得到无量纲振动方程,见附录公式(1).为方便表述,略去“*”,以下公式推导中符号均为无量纲形式.将得到的无量纲振动方程进行Taylor展开到三阶.由于有时滞项的存在,难以直接表示x和y方向上固有频率,因此进行以下处理[14]

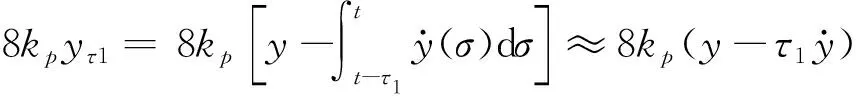
(8)

为应用多尺度法,在上述Taylor展开后的无量纲方程中引入小参数ε整理得

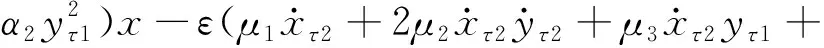
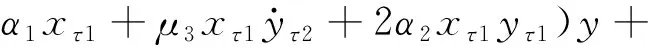
(9a)

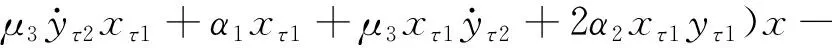
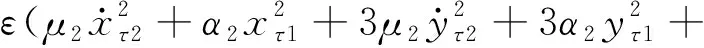
εeΩ2sinΩt

(9b)

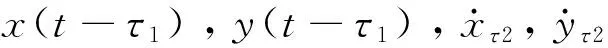
1.2 多尺度法摄动分析

应用多尺度法[15]求解无量纲振动方程(9),选取两个时间尺度,假设解为下列形式:

x(t,ε)=x0(T0,T1)+εx1(T0,T1)+O(ε2)

x(t-τj,ε)=x0τj(T0-τj,T1-ετj)+

εx1τj(T0-τj,T1-ετj)+O(ε2)j=1,2

y(t,ε)=y0(T0,T1)+εy1(T0,T1)+O(ε2)

y(t-τj,ε)=y0τj(T0-τj,T1-ετj)+

εy1τj(T0-τj,T1-ετj)+O(ε2)j=1,2

(10)

其中T0=t,T1=εt.T0为快时间尺度,T1,为慢时间尺度.

方程(9)中对时间的微分可通过(11)转化到新的时间尺度上.

(11)

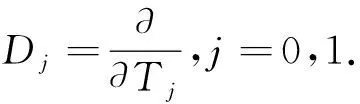
将(10),(11)带入方程(9)中,整理后分离ε的同次幂:

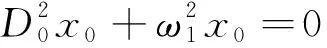
(12a)

(12b)

ε1为

6μ3x0x0τ1D0x0τ2+μ3y0y0τ1D0x0τ2+μ3(x0y0τ1+

y0x0τ1)D0y0τ2+α1(x0y0τ1+y0x0τ1)-

3μ3x0x0τ1D0x0τ2+μ1y0D0x0τ2+

2μ2y0D0y0τ2D0x0τ2-6μ4x0y0D0y0τ2+

eΩ2cos(Ωt)

(13a)

3μ3y0y0τ1D0y0τ2+μ3(x0y0τ1+

y0x0τ1)D0x0τ2+α1(x0x0τ1+y0y0τ1)-

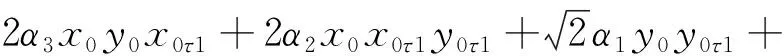
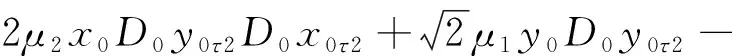
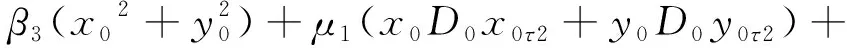
eΩ2sinΩt

(13b)

方程(12)的解为

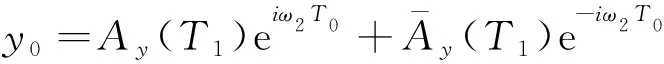
(14)

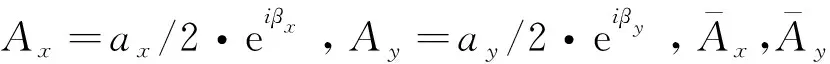
ετj)e-iω1(T0-τj),j=1,2

ετj)e-iω2(T0-τj),j=1,2

(15)

对Ax(T1-ετj)和Ay(T1-ετj)进行Taylor展开,由于ετj≪1,为方便推导有

Ax(T1-ετj)=Ax(T1)-ετjD1Ax(T1)+…≈Ax(T1)

Ay(T1-ετj)=Ay(T1)-ετjD1Ay(T1)+…≈Ay(T1)

(16)

考虑系统处于主共振、内共振、同时共振情况.为描述Ω,ω2与ω1的接近程度,引入频率调谐参数σ1和σ2,满足下列关系

Ω=ω1+εσ1,ω2=ω1+εσ2

(17)

将式(14)～(17)带入式(13),得到去除永年项的条件.分离其实虚部,并引入βx(T1)=εσ1T0-θx(T1),βy(T1)=θy(T1)+ε(σ1-σ2)T0,得到四个自治微分方程,见附录公式(3).

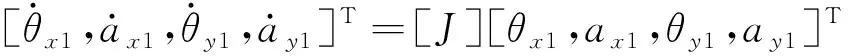
(18)

若式(18)中矩阵J的所有特征值均具有负实部,则该解为稳定解,否则为不稳定解.

2 计算结果及分析

为分析时滞反馈控制对转子-电磁轴承系统的作用,求解上述所得四个自治微分方程[见附录公式(3)]得到近似解,并利用MATLAB中ode45(τ=0)求解器及dde23(τ>0)求解器[17]求解式(9)以验证相同参数下利用多尺度法所得近似解.计算所用基本参数为:kp=1.5、kd=0.005、i0=0.2、ε=0.1、μ=0.01、σ1=0.如无特别说明,在下面的分析图中实线代表稳定解,虚线代表不稳定解.为了分析方便,本文认为无量纲位移信号时滞量τ1与无量纲速度信号时滞量τ2相等,即τ1=τ2=τ.

图3展示了水平和竖直方向稳态幅值随时滞量的变化曲线,时滞量的最大取值为转动周期.可以看到不同的时滞量会导致不同的振动幅值,并且稳定性也不同.定义使振幅小于τ=0时振幅的时滞范围为时滞量的“减振区域”.图3中标注“Suppression range”的范围内,任意一个时滞量下的振动幅值均小于τ=0时幅值,说明此时时滞有助于减小系统的振动.x方向该区域是τ∈[1.74,2.80],y方向该区域是τ∈[1.74,3.18],可见在x和y方向上虽然稳定解的范围一致,但“减振区域”并不一样,这是由于x与y方向上受力不同.

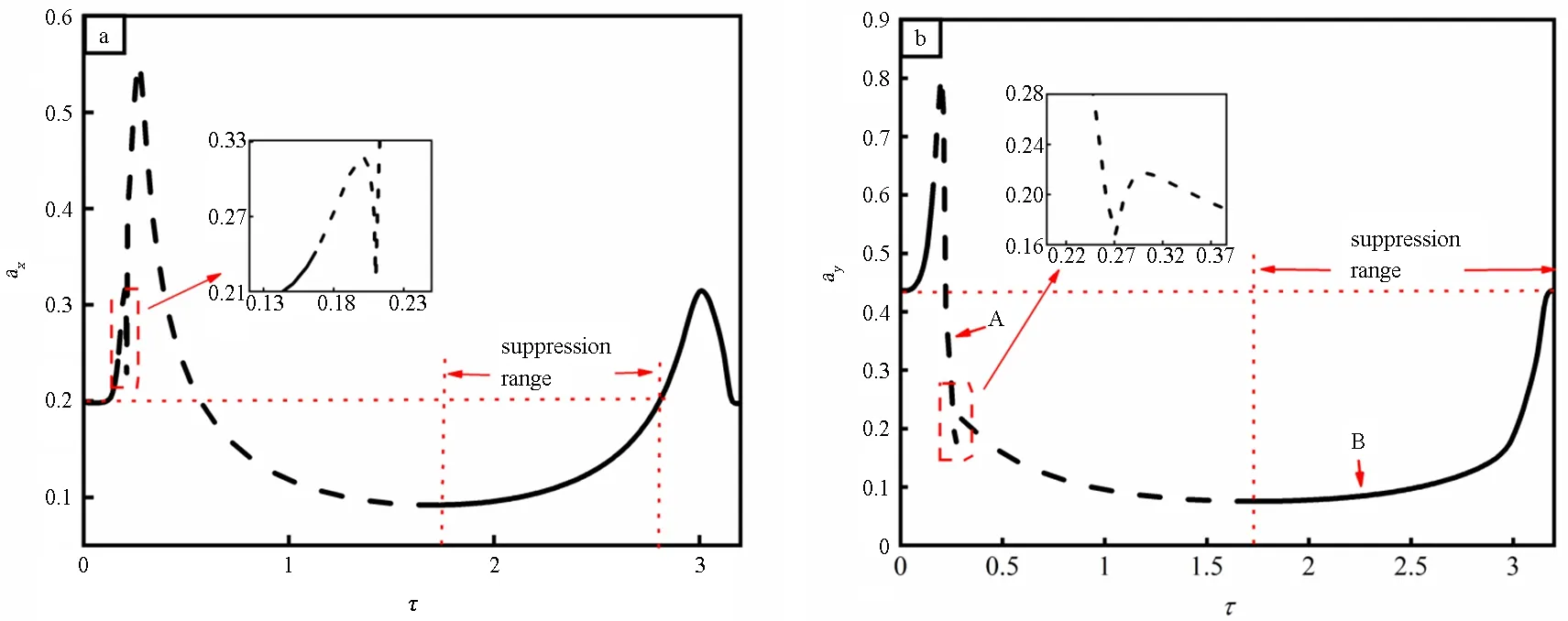
图3 无量纲时滞量-无量纲幅值曲线(实线代表稳定解,虚线代表不稳定解)Fig.3 Dimensionless time delay-dimensionless amplitude curves

图4展示了控制器中比例增益kp为1.3,1.5,1.8和2.2时的曲线,图5展示了微分增益为0.003,0.005,0.008和0.012时的曲线.对比之下,比例系数变化时曲线的形状变化更大.表1和表2分别统计了图4、图5中减振区域的区间,可以看到比例系数变化时减振区域的变化更大,当kp为2.2时减振区域由不连续的四个区间组成.对比表1和表2,微分系数增大对于减振区域影响较小.适当增大微分增益有助于提高系统阻尼,也可减小系统的振动幅值,但减振效果有限,因为过大的微分增益同时也放大了系统的高频噪声,使系统性能恶化.

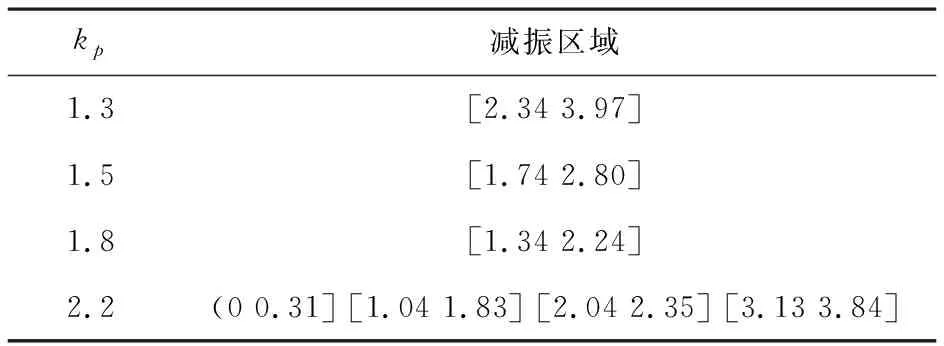
表1 不同kp的减振区域

表2 不同kd的减振区域

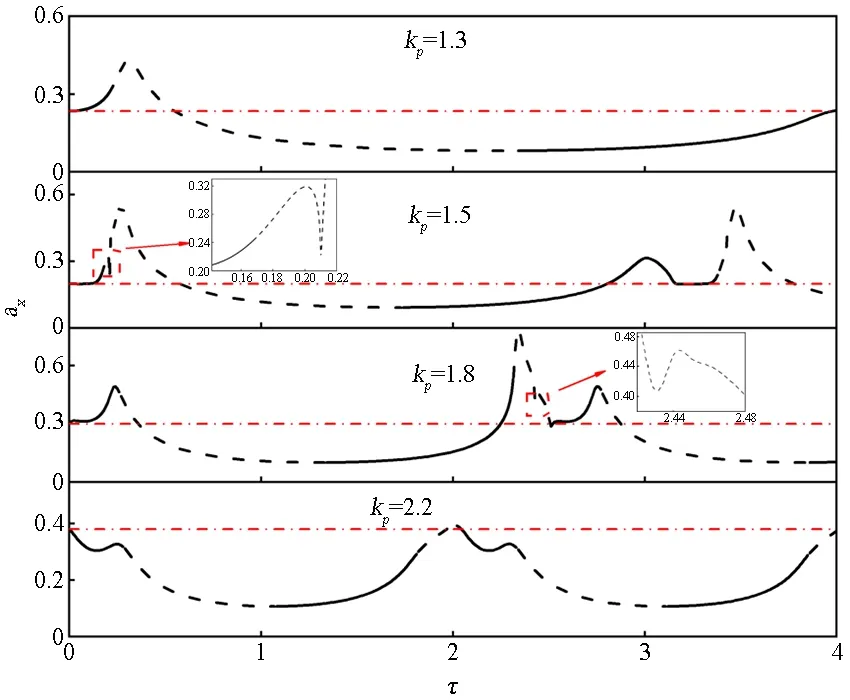
图4 不同比例增益kp时τ-ax曲线Fig.4 τ-ax curves at different proportional gains kp

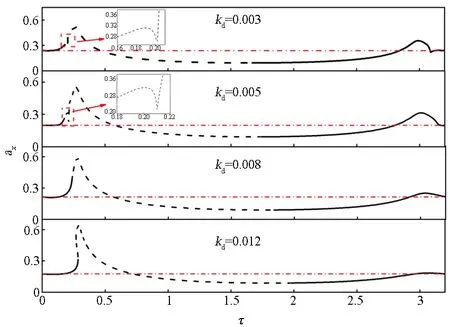
图5 不同微分增益kd时τ-ax曲线Fig.5 τ-ax curves at different differential gains kd

上面研究了转速与系统固有频率相等(σ1=0)情况下的减振效果.为研究其他转速下是否也具有减振效果,图6展示了图3(b)中A,B两点代表的时滞量以及情况下的幅频特性曲线.当τ=0时,系统在各转速范围内均稳定且幅值较小,而当时滞量为0.23时(点A),系统的共振区幅值明显增大,且在σ1∈[-0.052,0.052]范围内失去稳定性,这对转子的安全稳定运行造成很大威胁.当时滞量为2.3时(点B),系统在水平和竖直方向上主共振峰值均大幅减小,但当转速远离主共振情况时,时滞控制的效果不一定好,如图6(a)中σ1=-0.1,τ=2.3的幅值要高于无时滞振幅.

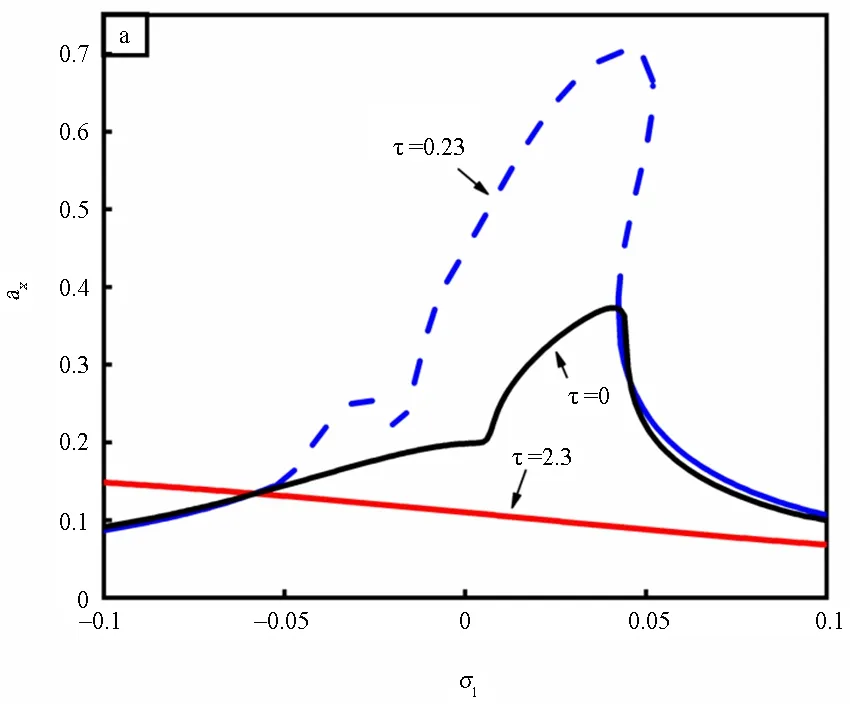
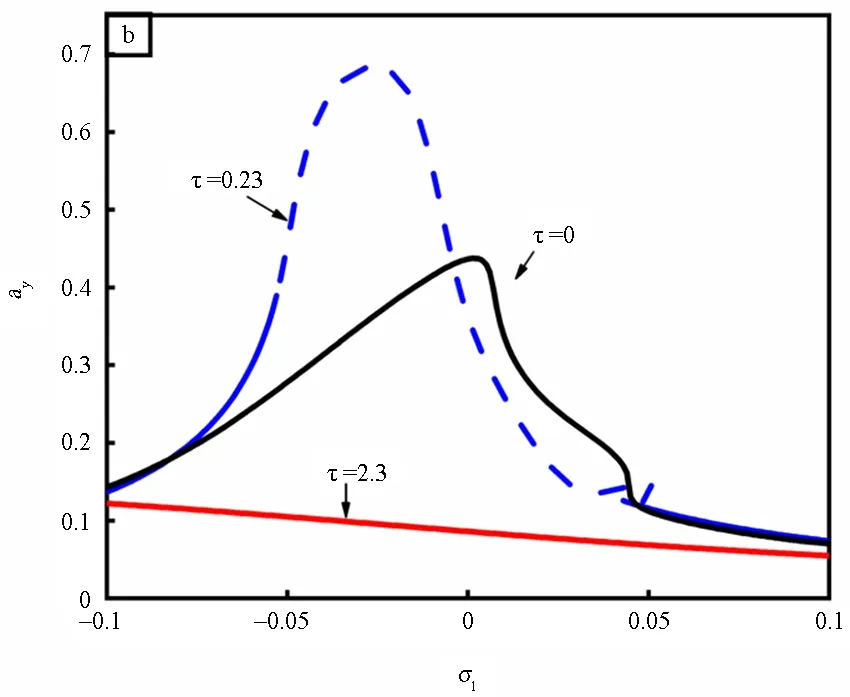
图6 不同转速下时滞控制的效果Fig.6 Effect of time delay control at different rotation speeds

图7展示了不同转速下时滞的“减振区域”.x和y方向上“减振区域”的分布并不相同,上方区域面积较大,包括了大多数σ1取值.x方向的上方减振区域左侧边界为σ1=-0.06,而在σ∈[-0.1,-0.06]区间内只有下方减振区域.图6和图7说明在转速变化时同一时滞量做不到全范围减振,此时可能根据需要进行时滞量参数的变化以适应减振需求.但在y方向上合适的时滞量是能做到σ∈[-0.1,0.1]范围内均减小振动.

转子不平衡是工程中较为常见的一个问题,质量偏心相当于对转子施加一个同频激励,使转子产生强迫振动.工程中若发现转子质量不平衡问题,一般需要停止设备运行并进行动平衡处理,费时费力.磁悬浮轴承具有可施加主动控制的优势,无需硬件改造,只需在算法上进行处理,即可对转子的不平衡响应进行抑制.图7展示了不同转速下时滞对无量纲偏心量-无量纲幅值曲线的影响.时滞量选取了图3“减振区域”中的τ=2.3.当τ=0时,由

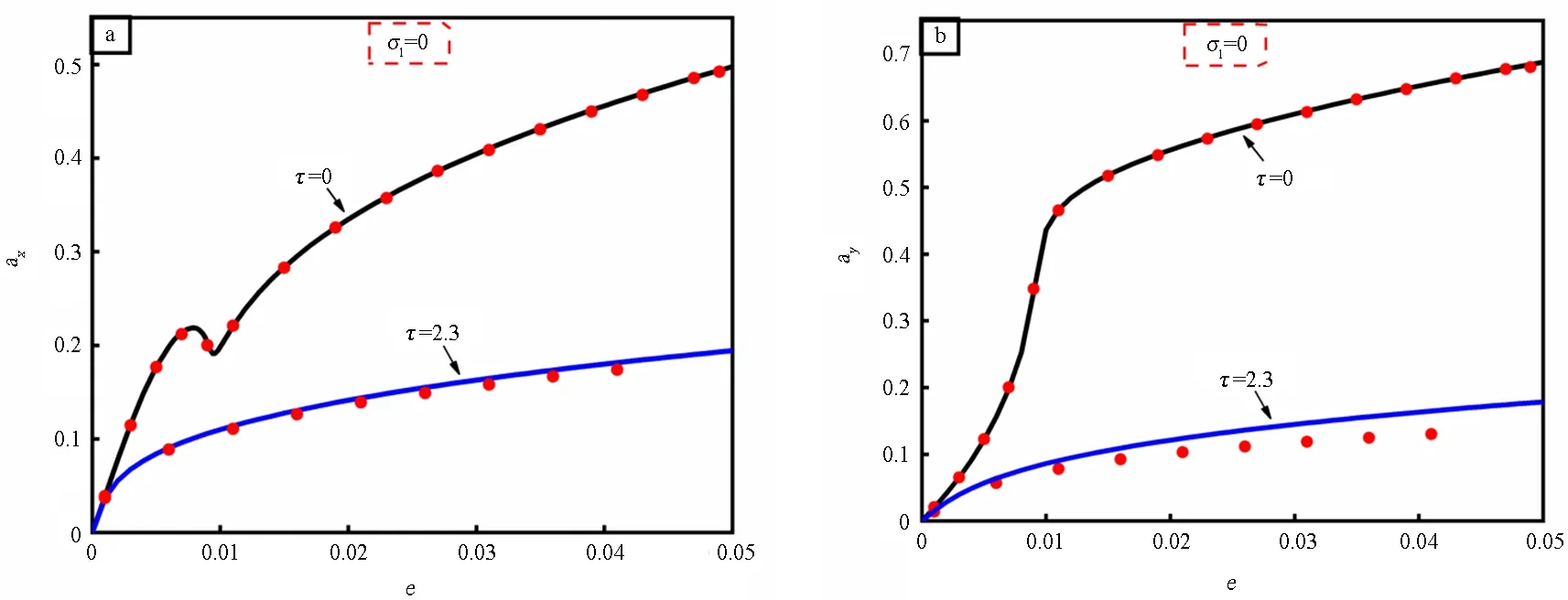
图8 加入时滞控制前后转子偏心量e-幅值曲线(红点表示数值模拟解)Fig.8 Eccentricity-amplitude curve before and after considering time delay (Red dots indicate numerical simulation solutions)

于电磁力的非线性以及电磁轴承的几何耦合,系统表现出许多非线性现象,如多值、突跳现象等.系统在某些转速范围内存在不稳定解,这使系统存在失稳的风险,如图7(c)(d)中虚线所示.当σ1时随着偏心量的增加转子振动幅值总体趋势是增大的,这是因为偏心量的增加相当于对转子的激励增大,因此振动幅值增大.当采用传统PD控制时(τ=0),系统在各偏心率下均保持稳定,但幅值较大;采用时滞反馈控制后(τ=2.3),系统在水平和竖直方向幅值均降低.当σ1=0.08时系统响应的对比,如图7(c)(d).采用线性PD控制时(τ=0),系统特性曲线出现不稳定区域,说明系统在某些偏心量下可能会发生失稳.加入时滞控制后(τ=2.3),不稳定区域消失,同时各偏心率对应的振动幅值也大大减小.红点表示通过MATLAB中dde23求得的数值积分解,与多尺度法所得近似解吻合良好.以上分析说明了时滞反馈控制对于最常见的转子不平衡问题具有良好的抑制作用.

3 结论

本文建立了时滞反馈控制下高速转子-电磁轴承系统的非线性模型,利用多尺度法求得方程的近似解并进行稳定性判定,利用MATLAB中dde23求解器验证近似解的准确性.主要研究了时滞反馈控制对于系统主共振峰值及稳定性的影响,并对时滞量的选取进行了分析,同时考察了时滞反馈控制对工程中最常见的转子不平衡问题的控制效果.主要结论如下:

(1)相对于微分增益,比例增益kp对时滞量“减振区域”影响较大.

(2)在某些时滞量取值下,转子振动幅值增大直至失稳,当时滞量取在“减振区域”时有助于减小转子振动幅值,增强运行稳定性.由于受力的不同,水平和竖直方向上“减振区域”并不相同.

(3)时滞反馈控制对于转子-电磁轴承系统的主共振峰值具有良好的抑制作用,但当转速变化时同一时滞量可能失去减振作用.

(4)时滞反馈控制对转子不平衡响应具有显著的控制效果,并且消除了一些非线性现象如多值、突跳等,具有广阔的应用前景.

在高速转子-电磁轴承系统的振动控制中,相对于其他复杂的控制算法,时滞反馈控制相对简单且容易理解.本文的研究结果表明其减振效果良好,具有广阔的应用前景,但伴随而来的问题是若时滞量取的不好甚至不对,系统将会失去稳定性.系统非线性与时滞的联合作用使得系统非常复杂,目前对于时滞量取值的理论指导还较少,多数情况下要依靠数值模拟结果,为此需要更多的研究.