解题研究:从解法研究走向解题教学设计
2023-11-15秦延延
秦延延
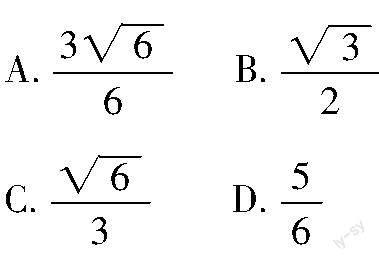








[摘 要] 针对中考较难题,教师往往不只局限在答案获取上,还会关注回顾反思阶段的一题多解与模式识别. 当然,更重要的是,要从解法的深度思考走向解题教学的精心预设. 包括预设出较难题的铺垫问题、引例问题、简化问题、等价问题、拓展问题等,再根据由易到难的方式渐次呈现,促进学生在解题学习中学会思考.
[关键词] 解题研究;自贡中考;深度思考;解题教学设计
每年中考试卷“新鲜出炉”之后,在一些自媒体公众号、“解题群”都能看到不少教师的解题热情,其中一题多解、巧思妙解、无字解法等“热度很高”.然而,解题研究还需要从“一题多解”走向“多解归一”,更需要从解法研究走向解题教学研究. 本文以一道2023年中考较难题为例,整理该题的解法思路与解题教学微设计,并进行反思.
由一道中考题的思路突破及解后反思说起
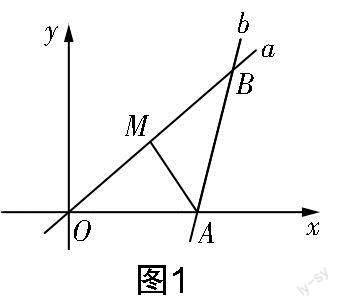
考题 (2013年四川省自贡市中考题)如图1所示,分别经过原点O和点A(4,0)的动直线a,b的夹角∠OBA=30°,M是OB的中点,连接AM,则sin∠OAM的最大值是( )
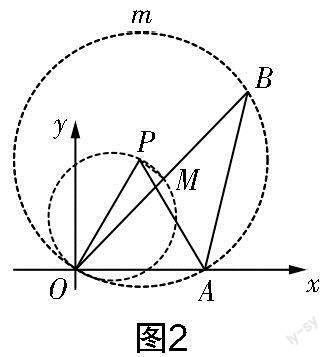
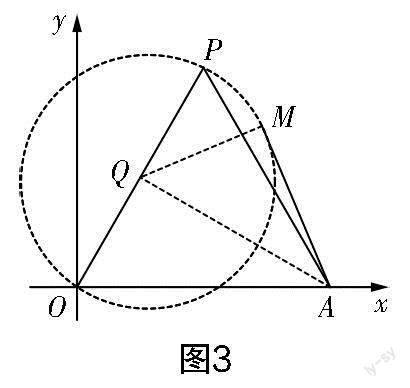
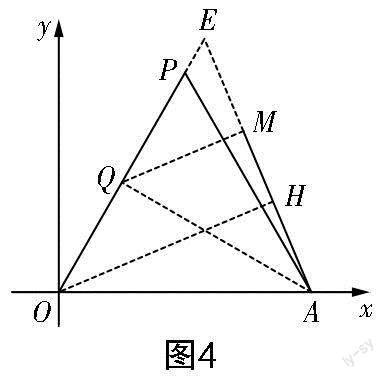
思路突破:观察△AOB,由已知条件可知OA为定长4,它所对的∠OBA是定角30°,于是可联想到“定弦定角”的解题经验,所以构造如图2所示的圆P(以OA为一边在第一象限取点P,构造等边三角形AOP,再以点P为圆心,PO的长为半径画出圆P,点B的轨迹是优弧OmA,不包括端点O,A). 接着思考OB中点M的轨迹. 如图2所示,连接PM,在大圆中由垂径定理得PM⊥OB,由此有∠PMO=90°,结合OP是定长,可知点M的轨迹是以OP为直径的圆的一段圆弧.接下来我们适当删除图2中的一些线条,得到如圖3所示的“简化”图形,进一步研究∠OAM何时取得最大值.
在图3中,点A是☉Q外一点,过点A作☉Q的切线AM(切点M在第一象限),此时∠OAM最大.
解后回顾:从上面的思路突破来看,以下两个“关键问题”值得重视,让我们“提取”分析如下.
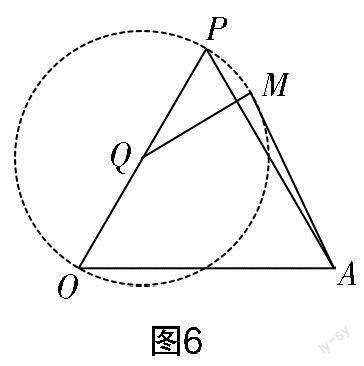
关键问题1:如图5所示,在△AOB中,AO=4,∠B=30°,点M是边OB的中点,分析点M的轨迹.
关键问题2:如图6所示,OP是☉Q的直径,点M在☉Q上,且P,M都在OA的同侧,当AM与☉Q相切时,求sin∠OAM的值.
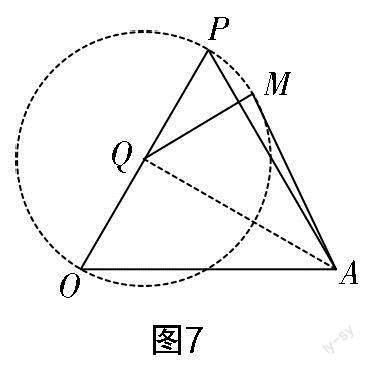
另解分析:对于“关键问题2”,还可以借助高中“三角公式”直接计算. 如图7所示,连接AQ,可分别求出∠OAQ,∠MAQ的正切值,然后运用两角和的正切公式,求出tan∠OAM的
教学环节1:基础热身
问题1:在△ABC中,AB=4,∠ACB=30°.
(1)当AC=BC时,求△ABC的面积.
(2)小明发现(1)中的情形,使得△ABC的面积取得了最大值. 你同意小明的发现吗?请说明理由.
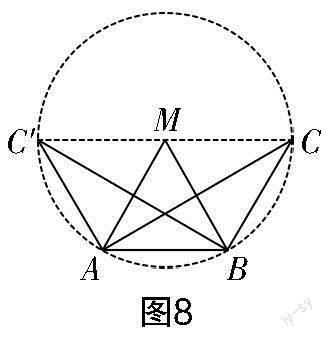
教学预设:第(1)问是“特例引路”,让学生感受到顶点C在AB边的垂直平分线上的特殊位置.而要解释第(2)问,则需要作出点C的轨迹(在一段优弧上). 第(3)问根据对称性质,如图8所示,有两个符合题意的点C,且都为等腰三角形. 教学时教师要请注意训练学生思维的严谨性.
教学环节2:拾级而上
问题2:如图9所示,在△ABC中,AB=4,∠ACB=30°,BD是△ABC的中线.
(1)分析中线BD的最大值与最小值;
(2)当∠ABD最大时,求中线BD的长.
教学预设:第(1)问的关键是
教学环节3:挑战考题
问题3:见上文“2013年四川省自贡市中考题”,解题时可参考上文的思路突破及解后反思,限于篇幅,这里略去.
教学组织:呈现考题后,教师要先引导学生独立思考,将问题的本质看清,再分离图形、简化问题,看出需要突破哪些关键步骤,与前面“教学环节”中已经研究的哪些问题等价,这样就可以快速“通过”较难步骤.对于思路较快的学生,可优先让他们讲解思路,再安排其他学生复述思路,让更多的学生都想通解题的关键步骤. 如果课堂时间不够,解题过程或一些细节可以留作课后进一步整理成解题笔记,而将课堂时间尽可能多地用在思路分析、关键步骤的突破上.
写在后面
笔者以为,“完整”的解题研究包括解题方法或思路的深度探究,含一题多解、多解归一、结构揭示、复杂问题或图形的分离与简化等;解题教学各个环节的精心设计,包括铺垫问题的预设、变式问题渐次呈现、较难题的思路启示等预设.而以上这些,都离不开教师持续修炼与精进命题改编的专业基本功.