例析函数思想在比较大小问题中的切入角度*
——兼谈解题思维的再创造
2023-11-10樊陈卫
樊陈卫
江苏省海门中学 (226100)
大小比较问题信息简洁明了,但题目串联起各类函数、不等式等诸多知识点,可以考察学生转化、数学结合、构造等诸多能力,成为包括高考在内的各级考试中的热门题型.函数思想是解决此类问题的一个重要方法,本文就函数思想在比较大小问题中切入角度进行一些剖析,现与同行分享,以期起到抛砖引玉之效.
一、比较对象具有相同结构



评注:函数求导时如果表达式比较复杂,不便直接求导,可采用整体代换简化函数表达式,再结合复合函数的方法判断单调性,也可以对目标函数先取对数再求导.对于自变量不在同一单调区间的两个函数值需要通过观察法将其中一个自变量进行等值转化到同一单调区间.构造函数过程中注意通过相同的结构构造函数的表达式,结构中不同数据作为自变量的取值.
练习已知9m=10,a=10m-11,b=8m-9,求证:a>0>b.
二、作差法中差的正负判断

分析:作差法是比较大小问题的基本方法,尝试a-b=(sin3α-sin3β)-3(lnsinα-lnsinβ)=(sin3α-3lnsinα)-(sin3β-3lnsinβ),由于(sin3α-3lnsinα)、(sin3β-3lnsinβ)有相同结构,故构造函数函数g(x)=x3-3lnx,a、c及b、c之间的大小比较思路类同.

评注:本题在判断差的正负时构造函数的思路与例1中构造函数的思路类似.

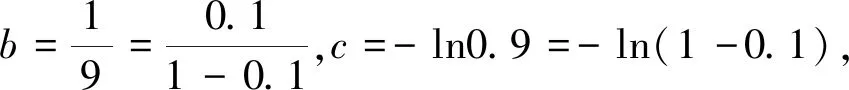

评注:待比较的各项都和某个常数有关,可将此常数设为变量x,再作差后可构造函数.如果发现直接作差,求导将会使差式复杂化(如本例中a,b比较),可考虑取对数再作差(求导)方法以简化运算.也可以考虑将差式中局部的需要判断正负的部分构造一个函数,利用求导办法确定正负(如本例中k(x)).
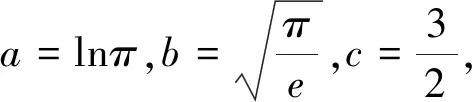
三、用泰勒展开式取近似值
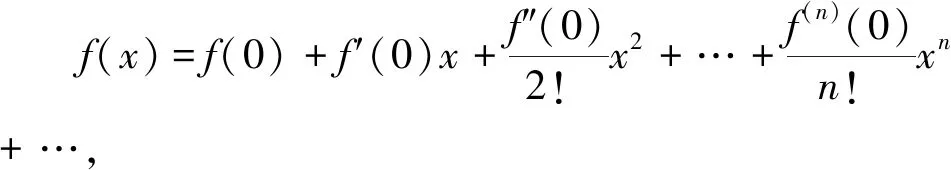


评注:利用泰勒展开式时应选择待比较项中绝对值小于1,尽可能接近于0的数据作为变量x来构造函数,然后根据函数在x=0处的泰勒展开式的前几项求出近似值.
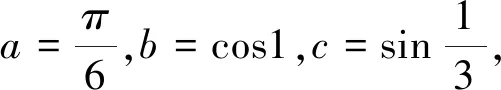
四、图像坐标表示待比较项
例5 已知a、b、c∈(0,+∞),且lna=a-1,blnb=1,cec=1,比较a,b,c的大小.

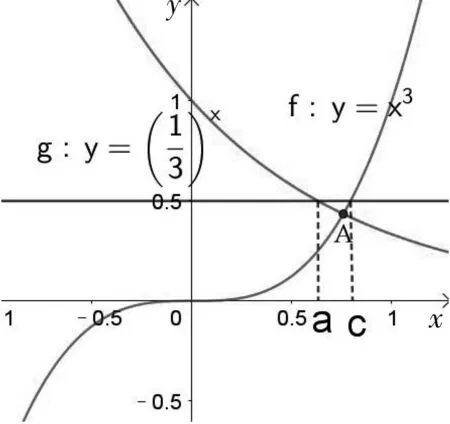
图2
评注:借助函数图像比较大小,一般需要将每一个比较对象构造为两个函数图像或一个函数图像与直线x=x0、y=y0的交点的横坐标或纵坐标,然后利用图像比较大小.如果比较对象是等式中的参数,对应的是图像交点的横坐标.


结语一把钥匙开一把锁,每一种方法都有对应的待比较项的特征,面对问题,需要学生关注比较项特征,找到针对性办法,特别有时候对比较项进行一定变形,才能和对应的方法发生关联.同时还应注意优化运算,化繁为简.
