优化解题反思 提升核心素养*
——以“解三角形问题”为例
2023-11-10郭海萍林新建
郭海萍 林新建
福建省福清第一中学 (350300) 福建省福清市教师进修学校 (350300)
解题中,学生常常出现考虑不周、浅尝辄止等现象,教师应有意识地引领反思,促使他们形成解题反思能力,发展其数学思维品质,以有效提升其核心素养.本文结合笔者的教学实践,就引领解题反思在提高数学核心素养上的意义和作用作一阐述,以飨读者.
1.引领错因反思,培育逻辑推理素养
对于解题,引领学生对错误原因作反思,不但可以找到改正错误的依据,而且还能充分显现学生的思维过程,促使他们进行全方位思考,逐渐由“误”到“悟”.


图1
显然,这样解答是不正确的,为了引导学生找出错因所在,笔者设置了如下问题引领反思.

问题2 你能找出发生错解的原因吗?
经过引领,学生反思,发现上述解法中,忽略了△ABC是锐角三角形这一条件,忽略了角的限制范围而导致周长范围过大,从而出错.
问题3 至此,我们要关注题设的隐含条件,那该如何纠正上述的错误解答呢?
经过引领,他们知道了应将∠OBC范围予以缩小.

评析:通过上述反思引领,学生经历了从错解到正解的反思改进的过程,也对思维活动各个环节、各个方面进行调整、校正,逐渐呈现出重论据、有条理、合乎逻辑性思维品质,推理论证能力得到了提高.无疑,逻辑推理素养得到了较好地培养.
2.引领解法反思,提高数学运算素养
对于数学解题,我们不能仅满足于正确的解答结果,还要重视对解法进行比较反思,以优化解答过程.笔者设置了如下问题引领学生对求解方法作反思.
问题4 本题还有其它更为直接和简洁的解法吗?
经过引领,学生自然想到了极端法,他们很快给出了如下解法.


图2

问题5 若将题目改为求△BOC面积的取值范围,用哪种方法更简捷?
学生很自然地选择了后一种方法,将问题得以简捷求解.
评析:通过上述反思引领,学生对解法进行了比较,经历了理解运算对象,探究运算思路,选择运算方法,解得运算结果的过程,思维也逐渐呈现出思路宽广、多方探索的特征,运算求解能力得到了提高.无疑,数学运算素养得到了较好地发展.
3.引领本质反思,提升数学抽象素养
我们理应将形异质同的问题进行归类,探索其解题规律,探求此类问题的本质,实现以点带面.为了对问题的本质有更深入的把握,笔者设置了以下问题引领反思.
问题6 解三角形问题的基本方法是什么?
经过引领,解三角形问题的基本方法是“知三求三”,即需要三个量以求出另三个量,通常有如下情况:①已知三边求三个角;②已知两边及一角求另一边两角;③已知一边及两角求另两边一角.
问题7 当条件不够时,若待求问题是最值(范围)问题,则应怎么办?
经过引领,认识到解三角形中的有关最值(取值范围)问题,当条件不够时,需引入一个新的变量,构造出待求最值关于这个变量的函数.这样,由于变量的引入,使得我们具备了运用通法“知三求三”解决问题的条件,进而将问题予以解决.
问题8 引入变量时要注意什么?
经过引领,认识到,要注意变量的取值范围,尤其是隐含在题设中的条件,要深入挖掘,避免疏漏而出错.
问题9 上述哪一种方法更具一般性?
显然,方法一更具一般意义,是解决此类问题的通法,其立意于函数思想,引入变量构造出待求最值关于这个变量的函数,进而用函数方法予以求解.其实,有许多解三角形中的有关取值范围问题都可以用函数思想、观点来解决,教师可以紧扣函数的本质,设置相关问题,让学生思考并理解其蕴涵的函数思想.可以思考如下问题:

解析:(1)易求得B=60°.
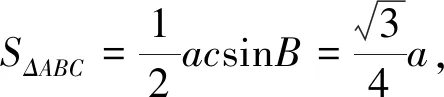



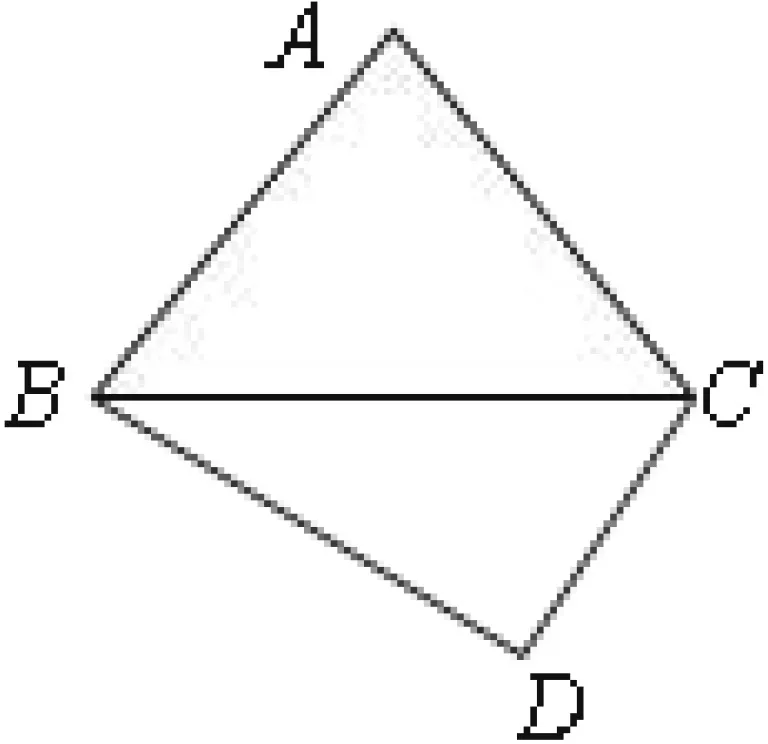
图3

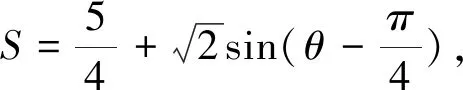
评析:通过上述反思引领,学生对问题进行了深入思考,经历了由此及彼、由表及里的思维过程,从事物的具体背景中抽象出一般规律和结构的过程,逐渐把握了事物的本质及问题的内在联系,抽象概括能力得到了提高.无疑,数学抽象素养得到了较好地发展.
总之,教师在教学中要加强解题后反思引领,这样才能使学生对数学问题的本质理解得更加透彻,对问题中所蕴含的数学思想体会得更加深刻.常此以往,学生的思维品质才会得到很大的发展,关键能力也会得到很好地提高,进而促进对学生数学核心素养的培育.
