立足学生本位 发展学科素养——对一道圆锥曲线题的探究及教学思考

余树宝 袁 悦

合肥师范学院数学与统计学院 (230601) 合肥工业大学附属中学 (230009)

圆锥曲线是高中数学的重要内容之一,在《普通高中数学课程标准》(2017年版2020年修订)中,对“圆锥曲线的方程”做了如下学业要求:能够根据不同的情境,建立椭圆、抛物线、双曲线的标准方程,能够运用代数的方法研究上述曲线之间的基本关系,能够运用平面解析几何的思想解决一些简单的实际问题．

纵观历年考题,圆锥曲线的考查多以考查圆锥曲线方程与几何性质,考查直线与圆锥曲线位置的关系为主,渗透着函数与方程、分类与整合、转化与化归、数形结合等主要数学思想,对学生的逻辑思维、运算求解等关键能力和直观想象、数学运算、逻辑推理和数学抽象等学科素养要求较高．

为此,笔者以2022年全国乙卷理科第20题圆锥曲线问题教学为例,谈谈自己的教学过程、设计意图以及教学思考,供同行参考．

1 考题再现

(1)求E的方程;

2 考题分析

这是一道探索创新情境试题,具体考查椭圆的标准方程、直线与椭圆相交的位置关系下动直线恒过定点等知识．

第(1)问是求解椭圆E的方程,核心条件是给出了椭圆上的两点坐标,核心考点是用待定系数法求椭圆的标准方程,问题的关键是椭圆方程应设为什么样的形式可以简化运算．

第(2)问是基于椭圆与直线相交来构建问题,在解题的过程中应先确定目标问题,然后为了实现这个目标,应明确需要的条件以及题目中给出的已知条件．此题的目标问题是动直线HN过定点,需要写出动直线HN的方程,并将直线方程整理成斜截式y=kx+m,接下来有两条途径可求定点:一是通过寻找k,m关系,求定点坐标;二是通过特殊位置发现定点,然后验证一般情况下动直线也过这一点．具体路径是先选择好主变量,求过定点P的动直线与椭圆相交于M,N两点坐标,然后依次求出T、H坐标,从而得到动直线HN的方程,最后说明动直线过定点．核心考点是椭圆与直线之间的位置关系,以及定点存在并求解．

3 教学设计

基于学生数学能力和素养发展,本节课以问题为导向,采取启发式、互动式、探究式教学法开展教学．

3.1 探究椭圆方程求解

问题1 椭圆的方程的形式有几种?求椭圆的方程常用什么方法?

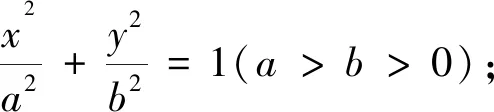
追问:你能确定本题中的椭圆的焦点位置吗?如果不能,我们该采用椭圆哪种形式的方程?

教师提醒学生在无法确定椭圆的焦点位置时,可考虑将椭圆方程设为Ax2+By2=1,这样可以避免对焦点位置的讨论．

设计意图:旨在回顾椭圆的方程的表达形式与求解方法,突出在求解椭圆方程的过程中,椭圆方程选择的重要性,好的选择有利于方程的求解．

问题2 完成第(1)问需要几步?请写出解答过程．

根据上述分析,结合椭圆的标准方程,大多学生应该能够独立梳理做题思路、表达解题过程．教师给予学生适量答题时间,待学生完成后,展示解题步骤,并针对科学性和规范性加以点评．

第一步(设方程):设椭圆E的方程为mx2+ny2=1(m>0,n>0,m≠n)．

追问：我们已经求出椭圆E的标准方程,你能否画出本题中椭圆的简图吗?

教师要求学生根据椭圆的标准方程快速画出椭圆简图,为接下来借图分析问题做好铺垫．

设计意图:旨在让学生通过独立完成解题过程,提高学生数学语言表达能力和规范书写能力．另外,建立图形与代数的联系,利用几何图形描述问题,借助几何直观理解问题,发展学生直观想象的数学学科核心素养,强调数形结合的思想在解决圆锥曲线问题的重要性．

3.2 探究动直线过定点

问题3 已知动直线l1的方程是y=kx+2,动直线l2的方程是y=(m+1)x+m,你能分别判断出l1,l2所过的定点坐标吗?

学生:对于直线l1,当x=0时,斜率k不影响y的值,此时y=2,所以直线l1过定点(0,2)．对于直线l2,可以将其直线方程整理成y=m(x+1)+x,当x+1=0,即x=-1时,m不影响y的取值,此时y=-1,所以直线l2过定点(-1,-1)．

设计意图:通过具体问题,帮助学生回顾并理解动直线过定点问题,旨在为第(2)的解决提供解题策略．

问题4 第(2)问中有几条动直线?哪条是主动直线?哪条是从动直线?动直线HN的位置最终取决于哪条动直线?

教师给学生思考的时间,进行小组讨论．

学生:三条动直线MN,MT,HN,其中过点P的直线MN是主动直线,其位置的变化影响着直线与椭圆相交的交点M、N,其中M点的变化决定点T的位置,从而影响点H的位置,所以动直线HN的位置最终取决于动直线MN．

此时教师再次提醒学生应当根据题意,先画出简图(如图1),并借助图形来分析．

图1

设计意图：旨在让学生感知本题中所涉及到的直线,除了直线AB,其余的都是动直线,并且各个交点都与主动直线MN存在着内在关系．

问题5 要确定过点P(1,-2)的动直线MN的位置,我们设直线MN的斜率为k,是不是最好的选择?

学生思考并回答．以往的解题经验告诉我们,若直线l斜率一定存在,则设直线方程为y=kx+m,否则均需要补充说明斜率不存在的情况．若直线l的斜率不可能为0,则可设直线方程为x=ty+n．此题中,显然直线MN的斜率不可能为0,所以我们为了避免讨论,我们最好设直线MN的方程为x=t(y+2)+1,即x=ty+(2t+1)．

设计意图：基于前面的分析,我们有必要先确定直线MN的方程．大多数学生习惯于设直线的斜率,易忽视斜率不存在的情形．另外,也基于减少运算量和运算步骤,提醒学生过定点的直线有两种设法．

问题6 接下来我们将按怎样的路径来走?

学生:先将直线MN和椭圆方程联立,得(4t2+3)y2+8t(2t+1)y+8(2t2+2t-1)=0．

追问1：需要求方程的根吗?

追问2：你能否根据M,T,H三点之间的关系,来表示出点H(xH,yH)的坐标吗?

学生:第一步先求点T的坐标,第二步再求点H的坐标．具体如下:

追问3:由点H,N的坐标能否将直线HN的方程写成y=○x+□的形式吗?

教师给予学生思考、计算的时间,锻炼学生的数学运算能力,并且板书运算过程．

追问4:为了证明直线HN过定点,有必要将○,□用变量t来表示吗?需要利用什么?

设计意图:教师通过层层设问,引导学生寻找解题路径,探究解题技巧,完成解题过程．并在问题解决的过程中,让学生体会数形结合、函数与方程等数学思想,提升学生逻辑推理、数学运算、直观想象等数学素养．

问题7 本题还有其它的解题路径吗?

教师给予肯定,并让学生课后再思考优化本题解题路径的好方法,下次课共享．

设计意图:旨在训练学生思维,寻求一题多解的方法,追求最佳解题路径,提高解题效率,积累此类问题解题经验．同时,这种解法先特殊后一般,可简化运算过程,也是解决定点问题的一种策略,这种方法体现了特殊与一般的思想．

4 教学思考

4.1 关注学生,实施问题导向

教学的出发点要围绕学生,尊重学生,适应学生,因材施教．因此,课堂教学中采取启发式、互动式、探究式的教学法,教会学生学会学习,充分体现学生主体地位,问题是数学的心脏,教学内容设计最好以问题为导向,将综合性强、思维量大的问题,化为一个个小问题串,引导学生由浅入深,循序渐进,点燃学生思维火花,激发学生求知欲望,持续让学生体会到问题解决成功的快乐．

4.2 总结方法,重视解题策略

波利亚说过,掌握数学就意味着善于解题．虽然圆锥曲线问题变化多样,但是题型总是有限的,且各种题型的解决方法和求解思路往往是有一定的规律性．常见的圆锥曲线问题,除本题中的曲线方程求解问题、定点问题,还有定值问题、最值或范围问题、探索性或存在性问题等等．备考复习时,建议教师多多引导学生学会分析和解决问题,多指导学生总结各种题型的通性通法,让学生不断积累解题经验,以便在应试时快速找到解题策略、完成解答过程．

4.3 渗透思想,发展数学素养

数学思想是解题的精髓．圆锥曲线问题的解决往往需要应用数形结合、转化、方程、特殊与一般等数学思想,来有效降低思维难度,简化解题过程,尤其是数形结合思想．尽管解析几何是用方程来研究曲线,但借助图形,利用曲线的几何性质仍是解析几何问题解决的有效手段．同时,圆锥曲线问题的解决,对学生的直观想象、逻辑推理、数学运算等数学核心素养要求较高,因此课堂教学时,要重视对学生的关键数学能力和核心数学素养的培养和发展,以适应具有选拔性的新高考．