不含短圈平面图的2-距离列表染色

俞家浩, 陈 敏

(浙江师范大学 数学科学学院,浙江 金华 321004)

0 引 言

本文仅考虑有限简单无向图.令G是一个图,若G能被嵌入平面中,使得任意2条边仅在端点处相交,则称G是可平面图;称长度为k的圈为k-圈;称G中最短圈的长度为G的围长,记作g(G).

图G的一个2-距离k-染色是指存在一个映射π:V(G)→{1,2,…,k},使得G中任意距离不超过2的顶点u和v都满足π(u)≠π(v);若G有一个2-距离k-染色,则称G是2-距离k-可染的;图G的2-距离色数通常用χ2(G)表示,定义为使得G有2-距离k-染色的最小正整数k的值.

图G的2-距离染色的概念最早由Wegner[1]于1977年引入并研究,他证明了每个Δ≤3的平面图是2-距离8-可染的,并提出以下猜想:

猜想1[1]令图G是最大度为Δ的平面图,则

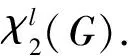
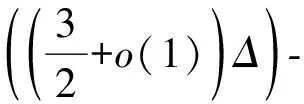
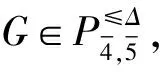
1 符号说明

接下来介绍一些文中常用的符号标记.令G=(V(G),E(G),F(G))为一个平面嵌入,其中V(G),E(G)和F(G)分别表示G的顶点集、边集和面集.

对于v∈V(G),用dG(v)表示v在G中的度数,即与v关联的边数,简记为d(v).若d(v)=k(d(v)≥k或d(v)≤k),则称v为G的k-点(k+-点或k--点).用Vk(G)表示G中所有k-点组成的集合,简记为Vk;令N(v)表示v的邻域;令N[v]=N(v)∪{v}表示v的闭邻域;v的一个k-邻点是指N(v)中度数为k的点.对于f∈F(G),边界上边的条数(割边算2次)定义为f在G中的度数,通常用dG(f)表示,一般简记为d(f).若f上的顶点按某一方向排序为v1,v2,…,vn,则记f=[v1v2…vn].如果2个面(圈)至少共用1个顶点, 那么称它们是相交的.

为了简便,一般用nk(v)表示v的k-邻点个数,用mk(v)表示与v关联的k-面个数,类似的定义可以运用在面上.关于本文图中的点,若该点的度数已经确定,则用实心点表示,否则用空心点表示.

2 定理1的证明

2.1 结构性质

为了方便,令Fπ(v)和Aπ(v)分别表示在染色π中v的禁用色集和可用色集.不难推断,Aπ(v)=L(v)Fπ(v).

引理1δ(G)≥2.

引理2假设v∈V2且N(v)={v1,v2},则

1)n2(v)=0.

2)若m3(v)=1,则d(v1)+d(v2)≥Δ+6.

引理3假设v∈V3且N(v)={v1,v2,v3},则

1)若d(v1)=2,则d(v2)+d(v3)≥Δ+3.特别地,当v2v3∈E(G)时,d(v2)+d(v3)≥Δ+5.

2)若3≤d(v1)≤10且v2v3∈E(G),则d(v1)+d(v2)+d(v3)≥Δ+6.

引理4假设v∈V4且N(v)={v1,v2,v3,v4},则

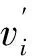
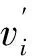
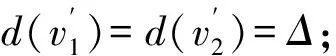
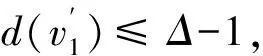
3)若d(v1)=2,则d(v2)+d(v3)+d(v4)≥Δ+2.特别地,当v3v4∈E(G)时,d(v2)+d(v3)+d(v4)≥Δ+4.

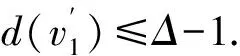
2)由题意得,d(v1)=d(v2)=2.在以下2种情形的讨论过程中,笔者都将构造一个G的2-距离L-染色,从而得到矛盾.

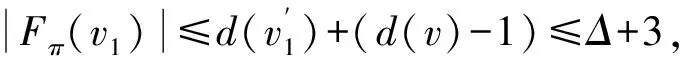
引理5假设v∈V5且N(v)={v1,v2,v3,v4,v5},则

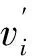
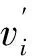
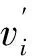
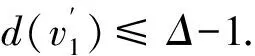
2.2 权转移

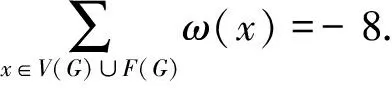
下面将证明对于每个x∈V(G)∪F(G),都有ω*(x)≥0,从而得到

矛盾, 因而定理1成立.

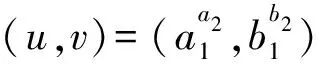
定义如下权转移规则:

R1:假设f是一个关联边uv的6+-面.

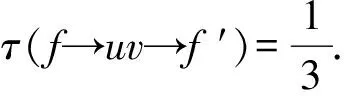
R1.2:否则,按如下操作:

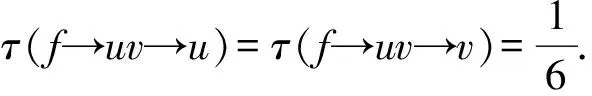
R2:假设v∈V2且uv∈E(G).

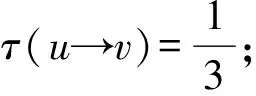
R2.2:若uv关联3-面且(u,v)=(6+,2),则τ(u→v)=1.

R3:假设v∈V3且uv∈E(G).

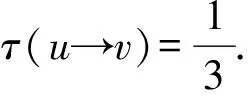
R3.2:若uv关联3-面f′=[uvw]且vx∈E(G),则

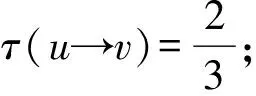
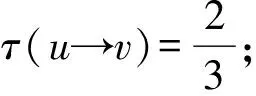
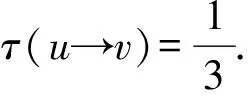
R4:假设v∈V4且uv∈E(G).

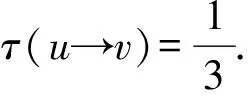
R4.2:若uv关联3-面f′=[uvw],则

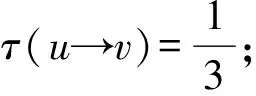
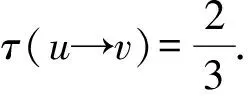
R5:假设P=uvw使得d(v)=2.

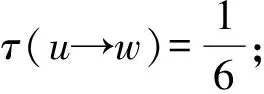
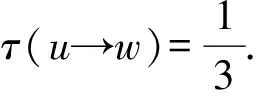
R6:假设uv∈E(G).

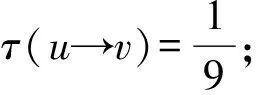
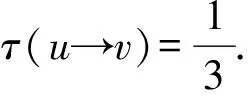
接下来通过断言1和断言2证明对于任意x∈V(G)∪F(G),都有ω*(x)≥0.

断言1对于任意f∈F(G),ω*(f)≥0.

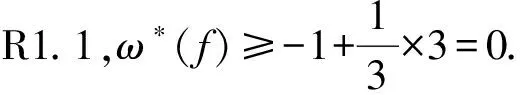
接下来,在断言2的证明过程中,有时为了便于叙述,令fi表示与点v关联的面,使得vvi和vvi+1为其边界上的2条边,其中i=1,2,…,d(v),且所有下标对d(v)取模.

断言2对于任意v∈V(G),ω*(v)≥0.

证明由引理1可得d(v)≥2.接下来,根据d(v)的值展开讨论.

1)d(v)=2,则ω(v)=-2.不妨设N(v)={v1,v2}且d(v1)≤d(v2).由引理1和引理2的1)知,d(v2)≥d(v1)≥3.由于G无重边,所以不难推出m3(v)≤ 1.

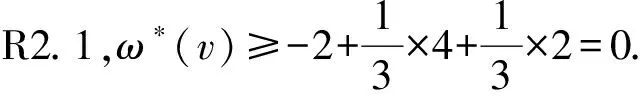
②m3(v)=1.由引理2的2)知,d(v1)+d(v2)≥Δ+6,这意味着v1和v2均为6+-点.根据R2.2,ω*(v)≥-2+1×2=0.

2)d(v)=3,则ω(v)=-1.令N(v)={v1,v2,v3}.不妨设d(v1)≤d(v2)≤d(v3).由引理3的1)知,n2(v)≤1.下面根据n2(v)的值展开讨论.

①n2(v)=1,即d(v1)=2.此时,v2和v3都是3+-点.鉴于G中无4-圈,可知m3(v)≤ 1.下面根据m3(v)的值进行讨论.

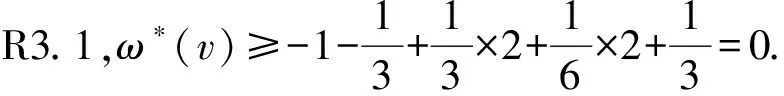
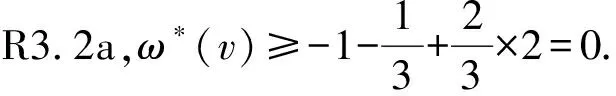
②n2(v)=0.同样地,鉴于G不含4-圈,有m3(v)≤ 1.下面根据m3(v)的值进行讨论.

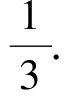
ii)m3(v)=1.不妨令d(f1)=3,则d(f2)≥6且d(f3)≥6.接下来根据d(v3)的值进行讨论.

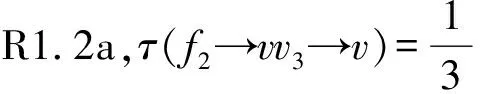
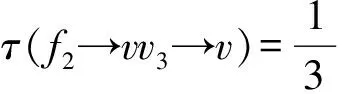
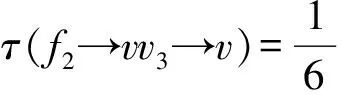
3)d(v)=4,则ω(v)=0.设N(v)={v1,v2,v3,v4}.由引理4的3)知,n2(v)≤ 3.因此,v仅仅给相邻的2-点转权.接下来,只需讨论1≤n2(v)≤3的情形.

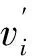
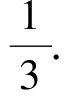
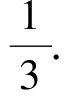
ii)m3(v)=1.此时,由引理2的2)知仅有1种可能,即i=2且d(f3)=3,从而有v3v4∈E(G).根据对称性,不妨设d(v3)≤d(v4).下面根据d(v3)的值分类讨论.

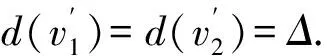
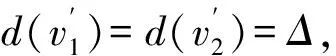
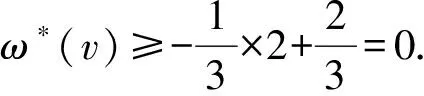
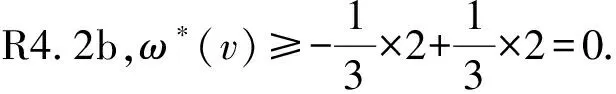
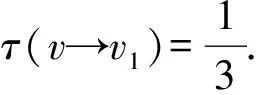
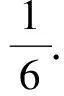
ii)m3(v)=1.由于对称性,不妨假设d(f3)=3,从而有v3v4∈E(G).接下来围绕d(v2)的值进行讨论.

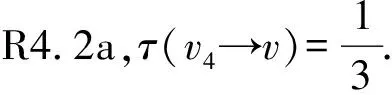
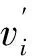
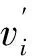
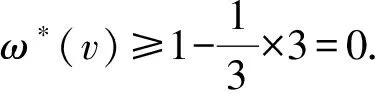
ii)m3(v)=1.此时,i=3且d(f4)=3,即v4v5∈E(G).不妨设d(v4)≤d(v5).下面的讨论围绕d(v4)的值展开.

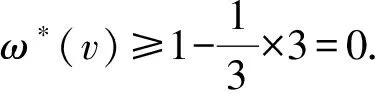
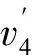
④n2(v)=2.不妨设d(v1)=d(vi)=2,其中i∈{2,3}.再一次,根据G中无4-圈的假设和引理2的2)可推断,m3(v)≤ 1.而且,m3(v)=1当且仅当i=2.下面根据m3(v)展开讨论.

ii)m3(v)=1.此时i=2.根据对称性,不妨设d(f3)=3,那么,v3v4∈E(G).进一步,不妨设d(v3)≤d(v4).下面围绕d(v3)的值进行讨论.

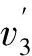
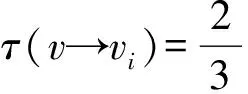
5)6≤d(v)≤Δ-2.同样地,为了便于计算,先估算一下v转给邻点vi的权值.

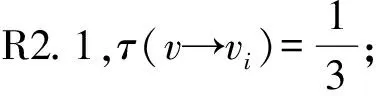
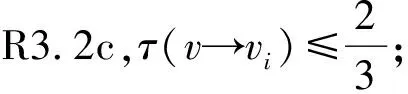
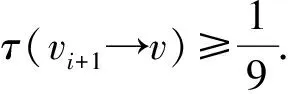
iii)当8≤d(v)≤Δ-2时,由R2.2知,τ(v→vi)=1.

根据以上讨论,可以得到如下结论:

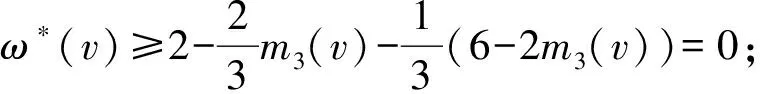
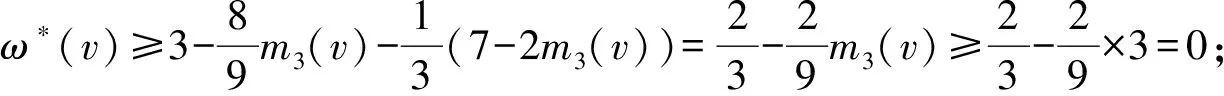
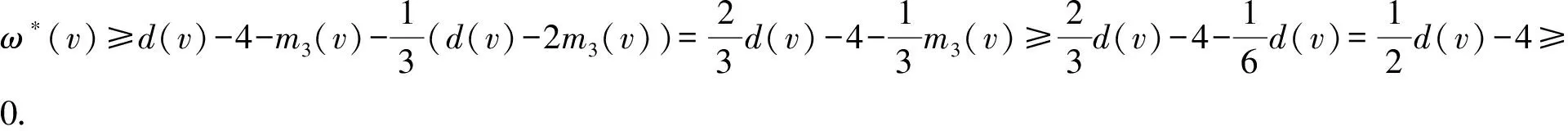
6)Δ-1≤d(v)≤Δ.类似地,先估算一下v转给邻点vi的权值.

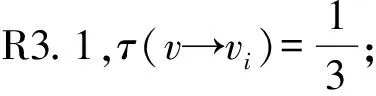
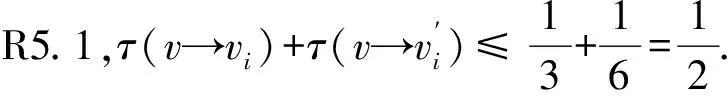
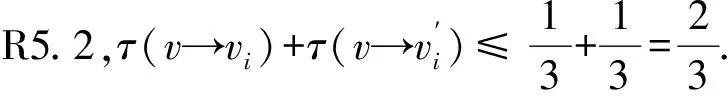
②vvi关联3-面.不妨设fi=[vvivi+1]为3-面且d(vi)≤d(vi+1).

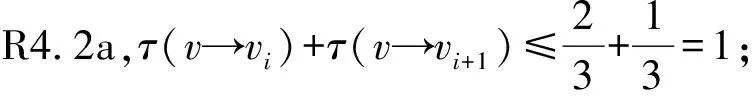
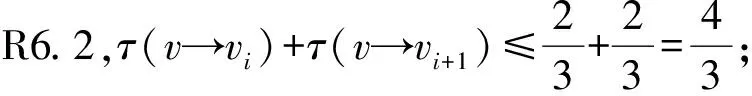
根据以上讨论,得到如下结论:

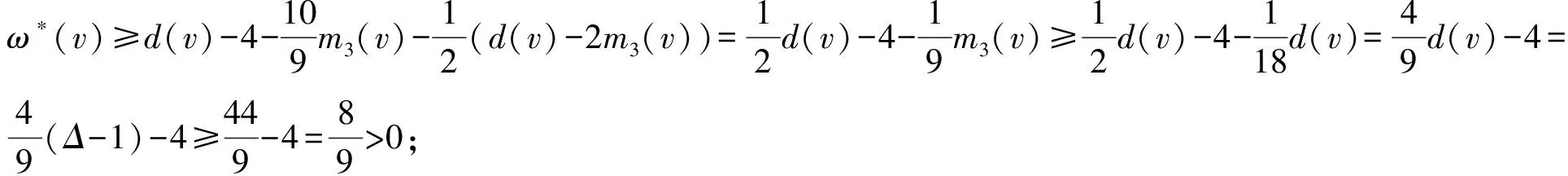
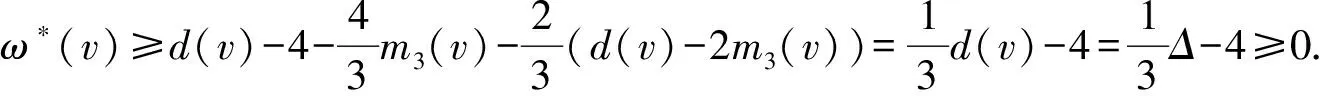
断言2证毕.

根据断言1和断言2得到,任意x∈V(G)∪F(G)满足ω*(x)≥0,因此,极小反例G不存在,从而定理1成立.

3 结 语

一直以来,关于不含4-圈和5-圈平面图的2-距离列表染色是热门的研究课题.作为文章的结尾,提出以下问题: