具有一般非线性项的拟线性Choquard方程的基态解

杨 宁, 沈自飞

(浙江师范大学 数学科学学院,浙江 金华 321004)

0 引 言

近年来,拟线性Schrödinger方程成为数学物理工作者关注和研究的重点之一.该方程具有丰富的物理背景,并在解释许多物理问题时发挥着重要的作用,如电磁波在介质中传播时出现的超流体薄膜方程、高功率超短激光的通道模型,以及量子力学理论中出现的物理现象等.

本文讨论的问题源于拟线性Schrödinger方程

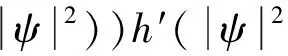
(1)

式(1)中:函数ψ:R×RN→C;V(x)为位势函数;k是实数;h,g为实函数.特别地,当k=1,h(s)=s时,将形如ψ(t,x)=e-iFtu(x)的驻波解(F为实数)代入方程(1)可得

-Δu+W(x)u-Δ(u2)u=g(x,u),x∈RN.

(2)

式(2)中:W(x)=V(x)-F是一个新位势;u为实函数.目前,已经有许多研究者利用变分原理对方程(2)进行了探究.文献[1]证明了方程(2)存在正基态解.随后,文献[2]利用约束极小化方法证明了方程(2)解的存在性.此外,文献[3]通过变量替换将方程(2)转化为半线性问题,并使用集中紧性原理克服紧性的缺失,最后在Orlicz空间框架下,利用临界点理论证明了方程(2)存在正解.

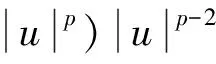
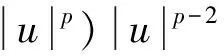
(3)

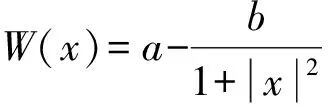
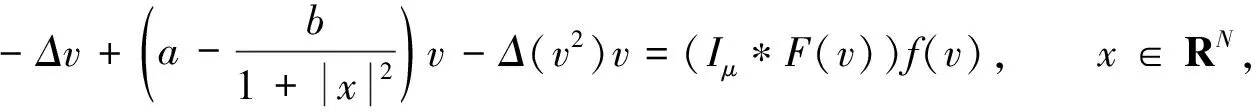
(4)

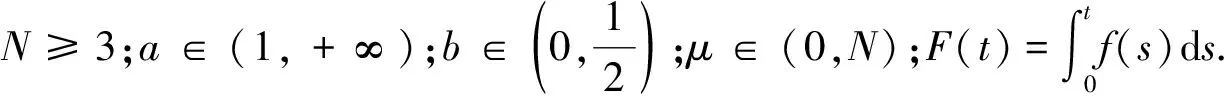
(f3)对任意t∈R,存在λ>2,使得0<λF(t)≤tf(t).

本文的主要结论为定理1.

定理1若非线性项f满足条件(f1)～(f3),则方程(4)存在一个基态解.

定理1改进了文献[4]中方程(3)的非线性项条件,得到更具一般性的方程(4),本文的结论推广了文献[4]的结果;同时方程(4)被赋予特定位势函数,不难验证该位势函数是径向对称的,据此,定理1可以看作是对文献[6]中结果的补充.

1 主要引理

为了处理方程(4)中的卷积项,还需如下Hardy-Littlewood-Sobolev不等式:

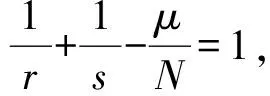
方程(4)所对应的能量泛函J(v):H1(RN)→RN为

引理2[8]变量替换函数g具有以下性质:

(g2)对任意s∈R,有g(s)≤|s|;

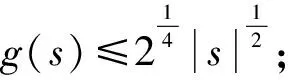
(g5)存在一个正常数C,使得

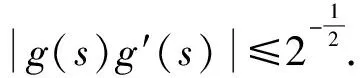
将v=g(u)代入能量泛函J(v),得到等价泛函为

而Ψ在H1(RN)中具有良好定义.由此可知,若u∈H1(RN)是Ψ的一个临界点,则v=g(u)是方程(4)的一个弱解.

下面回顾文献[9]中建立的一种间接性临界点理论.

引理3设(Z,‖·‖)为Banach空间,考虑Z中的一簇C1类泛函

Yξ(u)=R(u)-ξT(u),ξ∈Λ.

其中,Λ为R+中的区间.若T是非负的,则当‖u‖→+∞时,有R(u)→+∞或T(u)→+∞.假设Z中存在两点u1,u2,满足

其中,Γξ={γ∈C([0,1],Z):γ(0)=u1,γ(1)=u2}.对于a.e.ξ∈Λ都存在序列{un}⊂Z,使得:

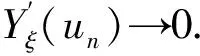
同时,映射ξ|→cξ是非减及左连续的.

当‖u‖→+∞时,有R(u)→+∞,且T(u)≥0.可见Ψξ(u)满足引理3的条件.

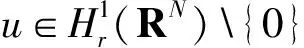
记P为方程(4)所对应的Pohožaev型恒等式,不难验证P=P1.

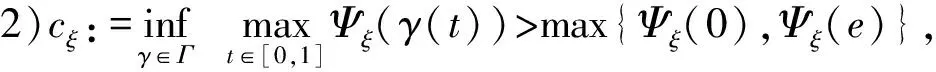
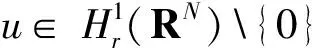
定义截断函数φ∈C0∞(RN),满足

φ(x)∈[0,1], |x| ≤1;φ(x)=0, |x|≥2.

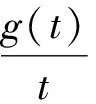
2)由文献[12]中引理3.3可知,存在常数C>0,ρ1>0,对任意‖u‖≤ρ1,有

同时,结合(f1)和(f3)可知,对任意的ε>0,存在Cε>0,使得

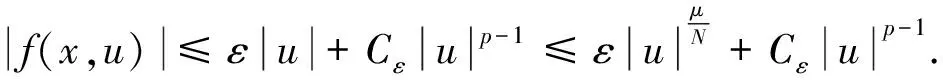
(5)

由式(5)及Sobolev嵌入定理知,对上述‖u‖,有

C‖u‖2-C‖u‖p.

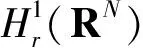
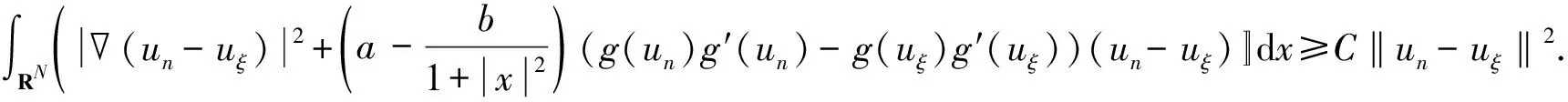
(6)

进而,结合式(6)、引理3、Hölder不等式及(g3)与(g6)可得

其中,p的范围与引理5一致.同理可推断出

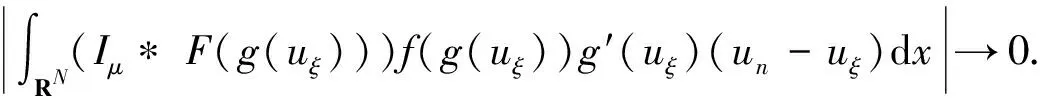
(7)

综合式(5)～式(7),有

C‖un-uξ‖2+on(1).

2 主要结果证明

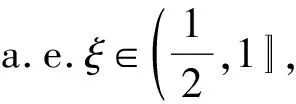
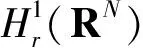
(8)

利用文献[13]中引理3.7,对式(8)进行部分缩放,得

(9)

结合式(8)和式(9)可知

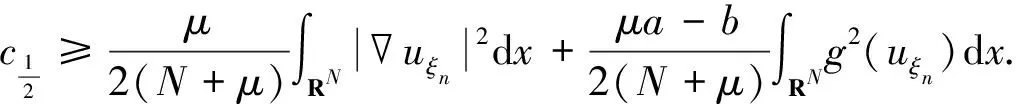
(10)

由(g5)以及Sobolev不等式可得

(11)

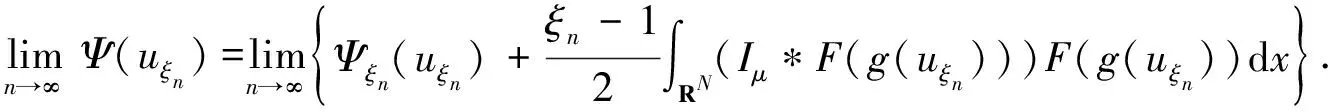
(12)

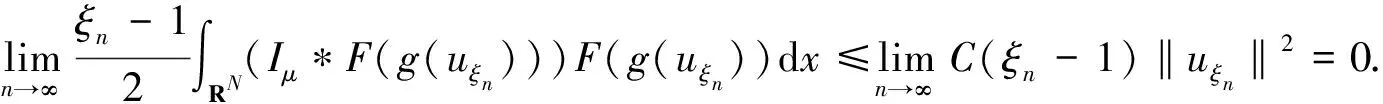
(13)

式(13)中,C为正常数.结合式(11)和式(12)可得

(14)

(15)

根据式(14)和式(15)可推断,{uξn}是关于Ψ:=Ψ1的有界PS序列.由引理6可知,存在Ψ的一个非平凡临界点u0,满足Ψ′(u0)=0,Ψ(u0)=c1.

3 结 语

本文利用变量替换法将拟线性问题转化为半线性问题,并使用变分方法证明方程基态解的存在性.由于文中所研究的方程(3)带有性质较好的位势函数,具有一定的特殊性,故在后续的工作中还可以考虑,当位势函数满足其他条件或非线性项具有更弱的假设限制时方程(3)解的存在性.