粗糙集的信息损失及其多阶定义

邓大勇, 汪 杰

(1.浙江师范大学 行知学院,浙江 兰溪 321100;2.浙江师范大学 计算机科学与技术学院,浙江 金华 321004;3.浙江师范大学 浙江省智能教育技术与应用重点实验室,浙江 金华 321004)

0 引 言

粗糙集理论[1-2]发展了40多年,产生了众多的粗糙集模型[3],这些模型基于各种关系,如等价关系、容差关系、邻域关系和模糊关系等.

虽然所有的粗糙集模型都有正区域(也称为下近似)、边界区域和负区域等3个区域,但大多数模型的属性约简定义都基于正区域,没有考虑边界区域和负区域.主要原因在于:定义粗糙集模型时,没能考虑模型的信息损失,使得很多粗糙集模型很难定义基于边界区域或负区域的属性约简.

研究信息损失的文献很多[4-5],但在粗糙集理论中讨论信息损失的文献很少.邓大勇等[6]在粗糙集属性约简过程中发现了信息损失,提出了一种在减少冗余条件属性过程中计算信息损失的方法.然而,目前还没有文献研究粗糙集定义中的信息损失问题.

本文研究粗糙集模型的信息损失及其多阶定义.在定义粗糙集的过程中,提出了计算信息损失的方法;根据模型的信息损失,把粗糙集分为零阶粗糙集、一阶粗糙集和二阶粗糙集;给出了具有较少信息损失的一阶粗糙集定义和无信息损失的二阶粗糙集定义;在一阶粗糙集和二阶粗糙集定义的基础上,分别提出了一阶粗糙集、二阶粗糙集的基于正区域、上近似、边界区域、负区域和粗糙集的属性约简;最后研究了这些属性约简之间的关系.本文的思想为粗糙集模型和属性约简的研究提供了一种新的思路.

1 粗糙集

本节简单介绍粗糙集的基本知识.

定义1[7]在信息系统IS=(U,A)中,概念Y⊆U的上近似、下近似分别定义为:

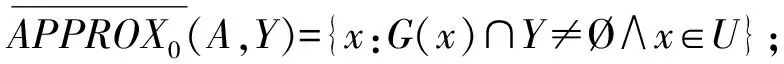
(1)

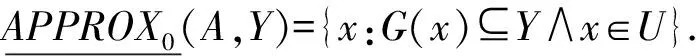
(2)

式(1)和式(2)中,G(x)是与x相关的信息粒.

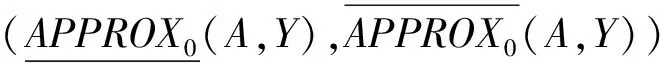
定义2[1-2]在决策系统DS=(U,A,d)中,正区域的定义为

(3)

式(3)中,Y∈U/{d}表示{d}对论域U的划分中的一个概念(等价类)．

定义3[1-2]在决策系统DS=(U,A,d)中,称B⊆A为属性约简(简称约简)当且仅当B⊆A满足下面2个条件:

1)POS0(U,B,d)=POS0(U,A,d);

2)对任意S⊂B,都有POS0(U,S,d)≠POS0(U,A,d).

2 信息损失

本节首先讨论运算∪所带来的信息损失,然后研究粗糙集定义过程中的信息损失．

2.1 运算∪的信息损失

在定义粗糙集的过程中,使用了运算∪.因此,下面讨论运算∪的信息损失问题.

假设运算∪是定义在论域U上,X,Y,Z是U的子集.若Z=X∪Y,则在得到结果Z之后,子集X和Y中的信息就损失了.但是,如果已经得到X,那么就很容易求出Y=Z-X.因此,在计算Z=X∪Y的过程中,在得到结果Z之后,可以将信息损失的部分视为X.

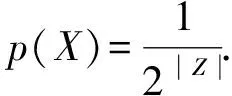
所以,运算∪的信息损失为

LOSS(Z,∪)=-log2p(X)=|Z|.

(4)

式(4)中,|Z|表示集合Z的势.

根据式(4)可知,对于单个个体x,在定义粗糙集的过程中,仅x的信息被保留下来,造成信息粒G(x)的信息损失.信息损失等于下近似(或上近似)中元素的个数.但因为上、下近似的不确定性,上、下近似的结果都是U的子集,可以近似地以具有确定性的U替代大、小不确定的上、下近似,因此,当元素x替换G(x)时,仅仅保留了x的信息,丢失了G(x)中的信息,可以近似地认为该定义下的粗糙集的信息损失为|U|-1(注:严格说来,信息损失小于等于|U|-1),也可近似地认为信息损失为|U|.

2.2 粗糙集定义的信息损失

在计算上近似和下近似时,往往会损失大量的信息.

当由信息粒G(x)获得下近似和上近似时,上、下近似中每个个体x都损失了其信息粒G(x)的信息,获取单个概念的上、下近似的信息损失计算如下:

在决策系统DS=(U,A,d)中,|U/{d}|个概念需要用下近似值和上近似值表示,也就是说,计算上、下近似时分别需要 |U/{d}|-1次∪运算.所以,正区域(下近似)的信息损失计算如下:

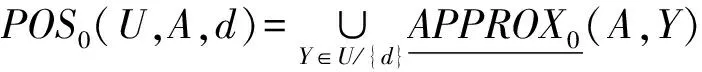
第1步,下近似的计算过程为:

…

第2步,计算信息损失

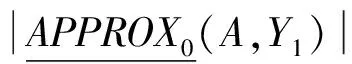
d)|≤(n-1)|U|.

综合第1、第2步可以简单理解为,在整个计算正区域的过程中进行了n-1次∪运算,每次∪运算的信息损失为|U|,所以,整个计算正区域过程中的信息损失为(n-1)*|U|.

3 粗糙集的重新定义

为了减少或避免粗糙集定义中存在的信息损失,需要对粗糙集进行重新定义.

在重新定义粗糙集之前,先引入了3类粗糙集模型,即零阶粗糙集、一阶粗糙集和二阶粗糙集.

假设论域为U,若粗糙集中的每个元素都是U中的一个元素,则称该粗糙集为零阶粗糙集;若粗糙集中的每个元素都是U的子集,则称该粗糙集为一阶粗糙集;若粗糙集中的每个元素都是U的幂集的子集,则称该粗糙集为二阶粗糙集.

根据三类粗糙集的定义,大多数粗糙集模型都是零阶粗糙集,它们在计算过程中损失了大量信息;而一阶粗糙集模型较少,包括三支决策[8-9]、F-粗糙集[10]和全粒度粗糙集[11]等,它们与相应的零阶粗糙集相比,所损失的信息较少;二阶粗糙集不损失信息,但当前缺乏二阶粗糙集模型的实例.

下面将在决策系统中提出一阶粗糙集模型和二阶粗糙集模型,并定义相应的属性约简,研究属性约简之间的关系.

3.1 一阶粗糙集

零阶粗糙集损失大量的信息,这使得其在决策系统中难以区分边界区域和负区域.为了更好地区分决策系统中的边界区域和负区域,本文定义一阶粗糙集模型.

定义4在决策系统DS=(U,A,d)中,一阶上近似和一阶下近似分别定义为:

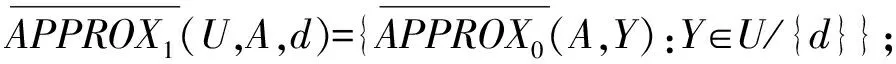
(5)

(6)

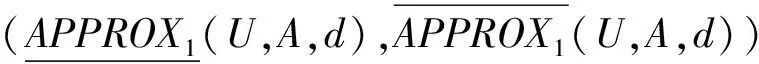
例1如表1所示,假设DS=(U,A,d)是一个决策系统,U={x1,x2,x3,x4,x5}是论域,A={a,b,c}是条件属性的集合,d是决策属性.

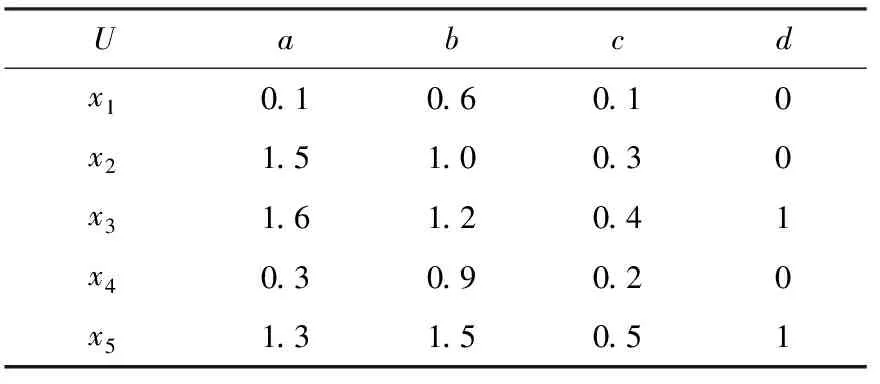
表1 决策系统DS=(U,A,d)

指定邻域半径为0.5,则G(x1)={x1,x4},G(x2)={x2,x3},G(x3)={x2,x3,x5},G(x4)={x1,x4},G(x5)={x3,x5},U/{d}={Y1,Y2}={{x1,x2,x4},{x3,x5}}.

Y1,Y2的零阶粗糙集为:

BND0(A,Y1)={x2,x3};

BND0(A,Y2)={x2,x3};

NEG0(A,Y1)={x5};

NEG0(A,Y2)={x1,x4}.

因此,可得到决策系统的一阶粗糙集为:

{{x1,x4},{x5}};

{{x1,x2,x3,x4},{x2,x3,x5}};

BND1(U,A,d)=

{BND0(A,Y1),BND0(A,Y2)}=

{{x2,x3},{x2,x3}};

NEG1(U,A,d)=

{NEG0(A,Y1),NEG0(A,Y2)}=

{{x5},{x1,x4}}.

在定义了决策系统中的一阶粗糙集后,就可以对所有不确定区域上的属性约简进行定义,具体如下:

定义5在决策系统DS=(U,A,d)中,称B⊆A为基于一阶粗糙集下近似的属性约简(如果不引起混淆,可以简称为约简)当且仅当B⊆A满足下面2个条件:

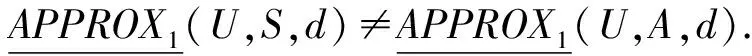
命题1在决策系统中,基于一阶粗糙集下近似的属性约简是其对应的基于零阶粗糙集下近似的属性约简的超集.

定义6在决策系统DS=(U,A,d)中,称B⊆A为基于一阶粗糙集上近似的属性约简(如果不引起混淆,可以简称为约简)当且仅当B⊆A满足下面2个条件:

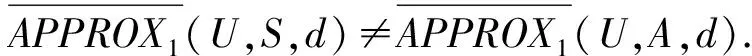
定义7在决策系统DS=(U,A,d)中,称B⊆A为基于一阶粗糙集边界区域的属性约简(如果不引起混淆,可以简称为约简)当且仅当B⊆A满足下面2个条件:

1)BND1(U,B,d)=BND1(U,A,d);

2)对任意S⊂B,都有BND1(U,S,d)≠BND1(U,A,d).

定义8在决策系统DS=(U,A,d)中,称B⊆A为基于一阶粗糙集负区域的属性约简(如果不引起混淆,可以简称为约简)当且仅当B⊆A满足下面2个条件:

1)NEG1(U,B,d)=NEG1(U,A,d);

2)对任意S⊂B,都有NEG1(U,S,d)≠NEG1(U,A,d).

定义9在决策系统DS=(U,A,d)中,称B⊆A为基于一阶粗糙集的粗糙集属性约简(如果不引起混淆,可以简称为约简)当且仅当B⊆A满足下面2个条件:

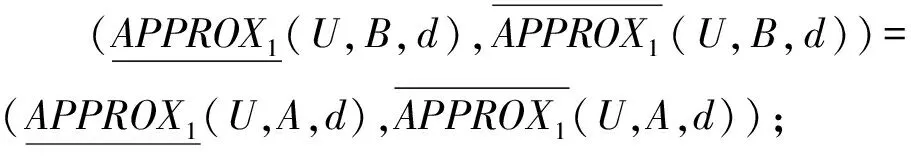
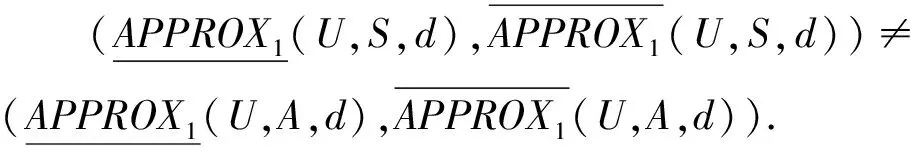
命题2在决策系统中,基于一阶粗糙集的粗糙属性约简是基于一阶粗糙集的其他属性约简的超集.

当前粗糙集的研究热点之一是三支决策[12-13],三支决策是一种典型的一阶粗糙集,它充分考虑了上近似、下近似和边界区域,并且给出了它们新的语义解释.F-粗糙集[10]则是在多个决策表中定义的一阶粗糙集,可以方便地研究动态数据、大数据,并进行概念漂移探测[14-15].

3.2 二阶粗糙集

在决策系统中,虽然一阶粗糙集比零阶粗糙集损失的信息少,但其同样也损失了信息粒G(x)中所包含的信息.为了避免信息损失,提出一个具体的二阶粗糙集模型.

在定义决策系统中的二阶粗糙集之前,先给出信息系统中的一阶粗糙集定义.

定义10在信息系统IS=(U,A)中,概念Y⊆U的一阶上近似和一阶下近似分别定义为:

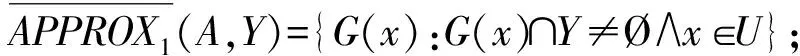
(7)

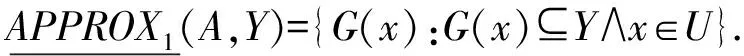
(8)

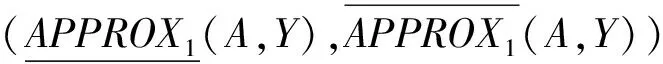
NEG1(A,Y)={G(x):G(x)∩Y=Ø∧x∈U}.

(9)

定义了信息系统中的一阶粗糙集之后,就可以定义决策系统中的二阶粗糙集,该粗糙集模型没有信息损失.

定义11在决策系统DS=(U,A,d)中,二阶上近似和二阶下近似分别定义为:

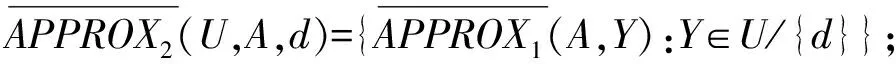
(10)

(11)

例2续例1,计算二阶粗糙集.

先计算信息系统中的一阶粗糙集,计算过程如下:

{G(x1),G(x2),G(x3),G(x4)};

BND1(A,Y1)=BND1(A,Y2)=

{G(x2),G(x3)};

NEG1(A,Y1)={G(x5)};

NEG1(A,Y2)={G(x1),G(x4)}.

于是,决策系统中的二阶粗糙集为:

{{G(x1)},{G(x4)},{G(x5)}};

{{G(x1),G(x2),G(x3),G(x4)},

{G(x2),G(x3),G(x5)}};

BND2(U,A,d)=

{BND1(A,Y1),BND1(A,Y2)}=

{{G(x2),G(x3)},{G(x2),G(x3)}};

NEG2(U,A,d)=

{NEG1(A,Y1),NEG1(A,Y2)}=

{{G(x5)},{G(x1),G(x4)}}.

正如决策系统中的一阶粗糙集一样,决策系统中所有不确定性区域的属性约简都可以定义在二阶粗糙集上.

定义12在决策系统DS=(U,A,d)中,称B⊆A为基于二阶粗糙集下近似的属性约简(如果不引起混淆,可以简称为约简)当且仅当B⊆A满足下面2个条件:

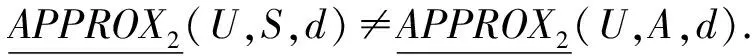
定义13在决策系统DS=(U,A,d)中,称B⊆A为基于二阶粗糙集上近似的属性约简(如果不引起混淆,可以简称为约简)当且仅当B⊆A满足下面2个条件:

定义14在决策系统DS=(U,A,d)中,称B⊆A为基于二阶粗糙集边界区域的属性约简(如果不引起混淆,可以简称为约简)当且仅当B⊆A满足下面2个条件:

1)BND2(U,B,d)=BND2(U,A,d);

2)对任意S⊂B,都有BND2(U,S,d)≠BND2(U,A,d).

定义15在决策系统DS=(U,A,d)中,称B⊆A为基于二阶粗糙集负区域的属性约简(如果不引起混淆,可以简称为约简)当且仅当B⊆A满足下面2个条件:

1)NEG2(U,B,d)=NEG2(U,A,d);

2)对任意S⊂B,都有NEG2(U,S,d)≠NEG2(U,A,d).

定义16在决策系统DS=(U,A,d)中,称B⊆A为基于二阶粗糙集的粗糙集属性约简(如果不引起混淆,可以简称为约简)当且仅当B⊆A满足下面2个条件:

2)对任意S⊂B,都有

命题3在决策系统中,基于二阶粗糙集的属性约简是其对应的基于一阶粗糙集的属性约简的超集.

命题4在决策系统中,基于二阶粗糙集的粗糙集属性约简是其他基于二阶粗糙集的属性约简的超集.

二阶粗糙集保留了粗糙集计算过程中的所有信息,特别是每个信息粒的信息,是一种不损失任何信息的全新的粗糙集模型.二阶粗糙集有望在一些要求无损信息的领域有一番应用.

4 结 论

针对传统粗糙集定义中的信息损失问题,提出了计算信息损失的方法,并按照模型的信息损失将粗糙集模型分为3类:零阶粗糙集、一阶粗糙集和二阶粗糙集.然后根据信息损失不同定义了一阶粗糙集和二阶粗糙集,引入了相应的属性约简,包括基于下近似的属性约简、基于上近似的属性约简、基于边界区域的属性约简、基于负区域的属性约简和基于粗糙集的属性约简.初步探讨了这些属性约简之间的关系.

本文为粗糙集模型的研究提供了一个新的视角,为粗糙集研究者及粒计算研究者提供一些有益启发.进一步研究包括基于一阶粗糙集和二阶粗糙集的属性约简方法、粗糙集模型变化方法和概念漂移检测方法等.