特征为2的素＊-代数上强保持2-新积

张芳娟，朱新宏

(1. 西安邮电大学 理学院，陕西 西安 710121；2. 中国兵器工业第203研究所，陕西 西安 710065)

设 ℜ 是*-代数. 对A,B∈ℜ，定义*[A,B]=AB-BA*,A·B=AB+BA*为A和B的2种不同的新积，新积的研究吸引了许多研究者的注意[1-10]

设 φ:ℜ→ℜ 是映射，对所有的A,B∈ℜ，有*[φ(A),φ(B)]=*[A,B]，称 φ 强保持斜交换映射；对所有的A,B∈ℜ，有*[φ(A),φ(B)]2=*[A,B]2，称 φ强保持 2-斜交换映射. 文献[3]证明了包含非平凡对称幂等元的单位素*-环 ℜ 上的强保持2-斜交换满射，得到φ(A)=λA对所有A∈ℜ成立，其中 λ∈CS且 λ3=1. 对所有的A,B∈ℜ，有 φ(A)·φ(B)=A·B，称 φ强保持新积；有 (φ(A)·φ(B))2=(A·B)2，称 φ强保持2-新积，其中(A·B)2=(A·(A·B))=A2B+2ABA*+BA*2. 本文将刻画特征为2的素*-代数上的强保持2-新积.

在证明主要结果之前，需要介绍一些概念. 令 ℜ 是*-代数.Z(ℜ) 是 ℜ 的中心.Q=Qml(ℜ) 是极大左商环，Q的中心C=C(ℜ)=Z(Q)叫做 ℜ 的可延拓中心. 对所有A,B∈ℜ，如果存在可加映射 *:ℜ→ℜ 满足(AB)*=B*A*和 (A*)*=A，则 ℜ 叫*-代数. 对任意x∈ℜ，若存在最小的正整数n，使得nx=0成立，则称ℜ的特征为n，记为 charℜ=n.如果这样的n不存在，则称 ℜ 的特征为 0.对任意A,B∈ℜ，若AℜB={0} 则A=0或者B=0，则称 ℜ 是素环. 注意到，素环的特征要么是零，要么是一个素数. 若 ℜ是素的，则Q也是素的且C是一个域. 若 ℜ 是素*-代数，对称可延拓中心CS={λ∈C:λ=λ*} 和斜对称可延拓中心CK={λ∈C:λ=-λ*}也是域. 并有Z(ℜ)⊆C.ZS(ℜ)和ZK(ℜ) 分别是 ℜ 上的对称中心元和斜对称中心元，其中ZS(ℜ)={A∈Z(ℜ):A=A*}，ZK(ℜ)={A∈Z(ℜ):A=-A*}.

下面使用Peirce分解. 在 ℜ 中取非平凡对称幂等元P. 若P2=P=P*，且P≠{0,I}，则P是非平凡对称幂等元，其中I是单位元. 设 ℜ11=PℜP,ℜ12=Pℜ(I-P)，ℜ21=(I-P)ℜP,ℜ22=(I-P)ℜ(I-P).设P1=P,P2=I-P，于是令 ℜi j=PiℜPj(i,j=1,2)，则 ℜ=ℜ11+ℜ12+ℜ21+ℜ22. 易得=ℜji,i,j=1,2.任取Xi j∈ℜ，则Xi j∈ℜi j.

定理1设 ℜ 是特征为 2 包含非平凡对称幂等元的单位素*-代数，φ:ℜ→ℜ 是满射. 对所有A,B∈ℜ，如果 φ满足 (φ(A)·φ(B))2=(A·B)2当且仅当对所有A∈ℜ，存在 α∈CS且 α3=I使得 φ(A)=αA，CS是 ℜ 的对称可延拓中心.

引理1[3]设 ℜ 是素环，令Ai,Bi,Cj,Dj∈ℜ(i=1,2,···,n,j=1,2,···,m)，使得对所有T∈ℜ都成立. 如果A1,···,An在C(ℜ的可延拓中心)上是线性无关的，则Bi在C上都是D1,···,Dm的线性组合. 类似地，如果B1,···,Bn是线性无关的，则Ai都是C1,···,Cm的线性组合. 特别地，如果对所有T∈ℜ有AT B=BTA成立，则A和B线性相关.

关于2-新积，有下面2个引理.

引理2设 ℜ 是包含非平凡对称幂等元的单位素*-环. 对所有X∈ℜ，存在S∈ℜ，使得 (X·S)2=0 当且仅当S=0.

证明充分性显然，只需证明必要性. 若P是 ℜ 上的非平凡对称幂等元. 由于 (PX·S)2(I-P)=0，所以对所有X∈ℜ，有PXPXS(I-P)=0.特别地，取X=P，有PS(I-P)=0.用X+P代替X得PXPS(I-P)+PXS(I-P)=PX(P+I)S(I-P)=0. 由于 ℜ是素的且P≠0，所以 (P+I)S(I-P)=0. 进而可得

S(I-P)=(P+I)S(I-P)-PS(I-P)=0.

类似地，由 ((I-P)X·S)2(I-P)=0得S P=0，所以S=S P+S(I-P)=0. 证毕.

引理3设ℜ 是特征等于2的素*-环. 对所有X∈ℜ，存在S∈ℜ，使得(S·X)2=0 当且仅当S2∈ZS(ℜ).

证明由于 ℜ 特征为2，. 若，则

反之，若对所有X∈ℜ，有 (S·X)2=S2X+XS*2=0. 由引理1知，存在 α∈C，使得S2=αI. 则对所有X∈ℜ，有X(αI+S*2)=0. 由 ℜ 是素的得S*2=-αI=-S2=S2，于是S2∈ZS(ℜ). 证毕.

定理1的证明充分性显然，下面的证明中假设 Char(ℜ)=2 和 φ:ℜ→ℜ 是强保持2-新积的满射. 下面通过8个断言证明必要性.

断言 1φ 是可加的.

对所有A,B,C∈ℜ，有 (C·(A+B))2=(C·A)2+(C·B)2. 则

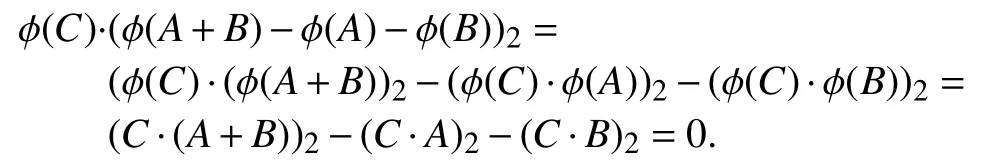
由 φ 的满射性和引理2得 φ(A+B)=φ(A)+φ(B).所以 φ 是可加的.

断言 2对所有非平凡对称幂等元P，任取X∈ℜ，有

设P∈ℜ 是非平凡对称幂等元. 由 φ的满射性得，对所有X∈ℜ，存在Y∈ℜ，使得X=φ(Y). 所以(φ(iP)·X)2=(φ(iP)·φ(Y))2=(iP·Y)2∈ℜ12+ℜ21.

断言 3对所有A∈ℜ，有 φ(A*)=φ(A)*.

对所有A,B∈ℜ，有=(B·A*)2A∈ℜB∈ℜ. 取，对所有，有

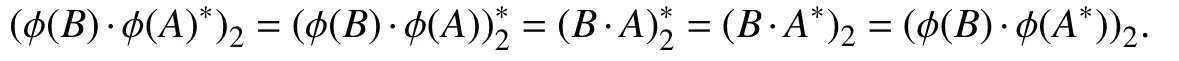
由 φ 的满射性知，对所有X∈ℜ，有 (X·(φ(A*)-φ(A)*))2=0.由引理2得 φ(A*)=φ(A)*.

断言 4存在 λ,μ∈CS，使得 φ(iP)2=λP+μ,λ≠0.

取P1=P,P2=I-P和 ℜi j=PiℜPj,i,j=1,2.存在Sij∈ℜij，使得

得，对所有X12∈ℜ12，有S21X12=0. 由 ℜ 是素的得S21=0.

类似可得S12=0.所以φ(iP1)2=S11+S22. 对所有X11∈ℜ11，由于 φ是满射，所以存在Y=Y11+Y12+Y21+Y22使得 φ(Y)=X11.则-Y12-Y21=(iP1·Y)2=(φ(iP1)·X11)2=S11X11+X11S11.由此，可得S11X11+X11S11=0， 进而由引理1得对所有X11∈ℜ11，存在 λ1∈CS，使得S11=λ1P1.类似可得，存在 μ∈CS，使得S22=μP2.所以 φ(iP)2=λP+μ 且 λ=λ1-μ∈CS. 下面证明 λ≠0，否则由引理3知，对所有X∈ℜ，有-P1X-XP1=(iP1·X)2=(φ(iP1)·φ(X))2=0.

矛盾.

断言 5φ(ℜii)⊂ℜ11+ℜ22,φ(ℜij)⊂ℜ11+ℜij+ℜ22,i≠j.

对所有X∈ℜ，由断言4知，

进而有

由(1)式知断言5成立.

断言 6对所有Xi j∈ℜi j，有 φ(Xi j)=-λ-1Xij,i≠j.

取X12∈ℜ12，由断言5得，存在Sii∈ℜii(i=1,2)，使得 φ(X12)=S11-λ-1X12+S22.

下面证明S11=S22=0.任取W21∈ℜ21，使得 φ(Y)=P1+W21.由断言5得Y∈ℜ11+ℜ21+ℜ22和P2(Y·X12)2P2=0. 所以

由W21的任意性和 ℜ 是素的得S11=0.类似地，由P1+W12得S22=0.所以对所有X12∈ℜ12，有φ(X12)=-λ-1X12. 同理可得，对所有X21∈ℜ21有 φ(X21)=-λ-1X21.

断言 7对所有Xi j∈ℜi j(i,j=1,2)，存在 δ∈CS且 δ3=I，使得 φ(Xij)=-iδXij.

令 φ(iP1)=S11+S22，有 φ(iP1)*=-φ(iP1).由断言5和断言6知，对所有X11∈ℜ11，X12∈ℜ12，存在Aii∈ℜii(i=1,2)，使得

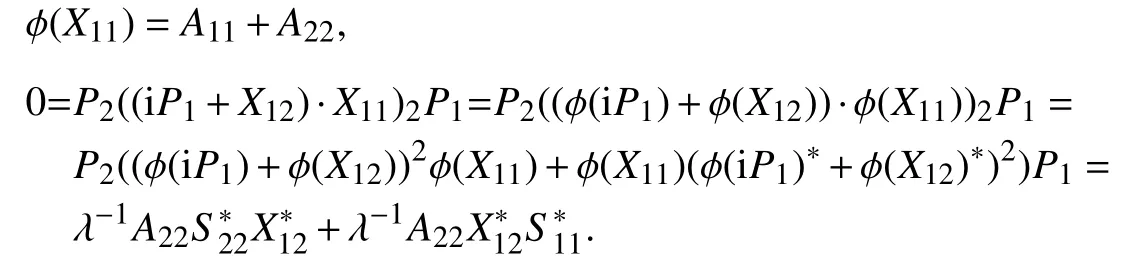
因此，对所有X12∈ℜ12，有

在(2)式中取X11=iP1，由引理1和P1≠0 得

于是存在 α∈CK，使得

下面证明S22=0，假设S22≠0，有S11=αP1，由(2)式和 ℜ 是素的得由α2P1=得 α≠0.由于S22≠0,μ≠0.由上面等式可得S22=αP2.则 φ(iP1)=S11+S22=α. 由此可得α2=φ(iP1)2=λP1+μ，由于 λ≠0，矛盾，所以S22=0.由得 μ=0,S11≠0.由(2)式知，对所有X12∈ℜ12，有=0. 进一步有A22=0，所以，对所有X11∈ℜ11，有 φ(X11)=A11.

同理可得，对所有X22∈ℜ22有 φ(X22)=B22.对所有X12∈ℜ12,X22∈ℜ22，有

由此可得，对所有X12∈ℜ12，有

取φ(P2)=T22.由于λ-1T22≠0，在(3)式中取X22=P2，由引理 1 得，存在 δ∈CS，使得S11=δP1.由于 ℜ 是素的，由得 δ2=λ.而且，对所有X12∈ℜ12，有

由此可得，对所有X21∈ℜ21，有iX21X11=-δ-1X21A11.所以A11=-iδX11.并且，对所有X11,Y11∈ℜ11，由(X11·Y11)2=(φ(X11)·φ(Y11))2=(-iδX11·-iδY11)2=iδ3(X11·Y11)2得 iδ3=I，进而有 λ-1=δ-2=iδ和φ(Xij)=-λ-1Xij=-iδXij，对所有Xi j∈ℜi j(i≠j) 成立. 类似，由((P1+X12)·X22)2得对所有X22∈ℜ22，有φ(X22)=-iδX22.

断言 8对所有A∈ℜ，有φ(A)=αA,α3=I,α∈CS.

由断言7和φ的可加性得 φ(A)=-iδA.令 -iδ=α，则 φ(A)=αA,α3=I,α∈CS. 定理1得证. 证毕.

由文献[11]得，若 ℜ 是素C*代数，则C(ℜ)=C,CS(ℜ)=R，由定理1有下面推论 1.

推论 1令 ℜ 是包含非平凡对称幂等元的单位素C*代数. 若 φ:ℜ→ℜ 是强保持2-新积的满射，当且仅当对所有的X∈ℜ，有 φ(X)=X.

由于von Neumann代数是包含许多非平凡对称幂等元的单位C*代数，又因为因子von Neumann代数是素的，所以由推论1有下面推论 2.

推论 2令M是因子von Neumann代数. 若 φ:M→M是强保持2-新积的满射，当且仅当对所有的X∈M，有φ(X)=X.