一类具有非线性密度制约的偏利合作系统

石志高

( 福建江夏学院 数理教研部， 福建 福州 350108 )

0 引言

近年来， 已有许多学者对种群具有反馈控制、 恐惧效应等的生态系统的动力学行为进行了研究[1-3]， 而对偏利合作种群系统的研究相对较少[4-6]。 祝占法等[4]研究了一方不能独立生存的两种群偏利合作模型:

式(1)中-b1表示第一种群的死亡率，b2表示第二种群的内禀增长率，a11，a22为密度制约系数，a12＞0 表示第二种群对第一种群的偏惠系数。 其中第二种群能对第一种群的生长起到促进作用， 而第一种群却对第二种群不起作用， 第一种群不能脱离开第二种群独立生存。 文[4]分析了在污染中偏利共生的两种群持续生存与绝灭的阈值。 文[7]在文[4]的基础上研究了具反馈控制的一方不能独立生存偏利合作系统的稳定性。文[8]研究了具有相互干扰的捕食-食饵系统，模型如下:

式(2)中r1，r2，a1，e，l均为正常数，k ＞0 表示捕食者种群的最大环境容纳量，0＜θ ＜1 表示捕食者之间的相互干扰系数，文[8]给出了正平衡态全局稳定的充分条件。 受上述研究结果的启发，笔者考虑一类具有非线性密度制约的偏利合作系统:

式(3)中a1，a2，b1，c1，c2均为正常数， 考虑α＞0 且α≠1 的情形。-a1表示第一种群的死亡率，a2分别表示第二种群的内禀增长率，b1xα表示第一种群的非线性密度制约项，c1表示第二种群对第一种群的偏惠系数，c2表示第二种群密度制约系数。 由系统的实际意义， 仅在＝对系统(3)进行讨论。

1 预备知识

定义1[9]对驻定微分方程组，y∈D⊆Rn， 方程组f (y) ＝0 的解y ＝y*表示为相空间中的点， 它满足微分方程组， 故称为平衡解(驻定解、 常数解)， 又称为奇点(平衡点) 。

定理1[9](Bendixson-Dulac 判别法) 若在单连通区域G内存在函数B(x，y)∈C1(G)， 使得， (x，y) ∈G，且不在G的任一子区域内恒为零， 则系统不存在全部位于G内的闭轨线和具有有限个奇点的奇异闭轨线。 其中函数B(x，y) 常称为Dulac 函数。

2 主要结论

引理11) 当时， 系统(3) 只有平衡点O(0， 0)； 2) 当时， 系统(3) 有平衡点O(0， 0) 和正平衡点A(x*，y*)， 其中x*。

证解方程组可得以下两个等价方程组:

由

定理21) 当时， 平衡点O(0， 0)是鞍点； 2) 当时， 平衡点O(0， 0) 是鞍点， 正平衡点A(x*，y*) 是稳定的焦点或结点。

证由系统(3)对应的雅可比矩阵

定理3系统(3) 是持久的。

证由系统(3) 的第二个方程可知:。 对充分小的ε ＞0， 存在T ＞0，当t ＞T时， 有， 从而有。 再由系统(3) 的第一个方程， 可得:

定理4系统(3)的正平衡点A(x*，y*)是全局渐近稳定的。

证由定理2 可知正平衡点A(x*，y*) 是局部渐近稳定的， 如果系统(3) 在G＝内不存在闭轨线， 那么该平衡点就是全局渐近稳定的。 取Dulac 函数B(x，y)＝x-1y-2， 则有b1αxα-1y-2＜0。 由Dulac 准则可知， 系统(3)在上不存在极限环，从而正平衡点A(x*，y*) 是全局渐近稳定的。

3 数值仿真

通过改变第一种群非线性密度制约项b1xα中的α值， 分别作系统的轨线图， 通过观察轨线的变化， 解释第一种群受非线性密度制约的影响。

例1取a1＝1，a2＝3，b1＝2，c1＝3，c2＝4，， 考虑系统:

图1 系统(4)两种群系统轨线图

图2 系统(4)两种群系统相图

例2仅改变第一种群非线性密度制约项b1xα中的α值， 取α＝3， 其余参数不变， 考虑系统:

图3 系统(5)两种群系统轨线图

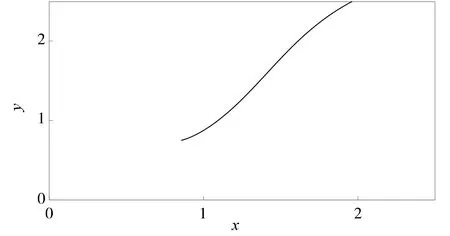
图4 系统(5)两种群系统相图

4 生态意义

本文两种群并不是相互依赖的， 第一种群对第二种群不起作用， 而第二种群能对第一种群的增长起促进作用， 而且第一种群不能脱离开第二种群独立生存。 系统(3) 的正平衡点是全局渐近稳定的， 且在正平衡点附近不存在闭轨线， 可见两种群的数量在一定时期内不会稳定不变， 而是不断地变化， 随着时间的推移逐渐趋于稳定，如果第二种群灭绝， 那么第一种群因受自身密度制约也将面临灭绝。