Impact of Phase Noise on TDMS Based Calibration for Spaceborne Multi-Beam Antennas
2018-04-04YujieLinXiangyuanBuShuaiWangYuanChaiJianpingAn
Yujie Lin, Xiangyuan Bu,*, Shuai Wang, Yuan Chai, Jianping An
1 School of Information and Electronics, Beijing Institute of Technology, Beijing 100081, China
2 Institute of Telecommunication Satellite, China Academy of Space Technology, Beijing 100094, China
* The corresponding author, email: bxy@bit.edu.cn
I. INTRODUCTION
Multi-beam antennas (MBAs) equipped in satellite communications systems have attracted growing attention recently due to their flexibility to control beam patterns and their potential to cover the service areas with high-gain spot beams [1]-[3], thereby improving the communication capacity and the spectrum utilization dramatically [4]. Accurate beam pointing is achieved by precise control of attenuators and phase shifters for each element to exhibit the de fined excitations in amplitudes and phases.However, electronic components of the satellite payload suffer from inevitable perturbations in the harsh space environment, such as temperature drift, aging [5], and single event upset (SEU), causing amplitude and phase errors [6], [7]. Therefore, accurate calibration is of crucial importance to maintain the optimal performance of space-borne MBA systems [8].
Various kinds of calibration techniques have been proposed to obtain the amplitude and phase characteristics for MBA systems in orbit, which can be distinguished into two major categories, i.e., external calibration methods [9] and internal calibration methods [10],[11]. External calibration methods employ an additional source located in the fixed far- field region of the array aperture for monitoring purposes. One drawback of these methods is that the calibration performance is subjected to the space communication link [12], such as the path loss, fading, multipath, near-field scattering, etc. Another drawback is that it is difficult to satisfy the far-field conditions for large-aperture and high-frequency antennas.On the contrary, internal calibration methods inject a dedicated calibration network through coaxial cables to couple parts of the signals back to the calibration receiver. The physical connection ensures that the calibration process is performed with the least disturbance. The internal calibration method has been successfully veri fied in a spaceborne environment by TerraSAR-X launched in 2007 [11].
With the scale of spaceborne MBAs enlarging continuously [13], the implementation cost of the internal calibration receiver is tremendous and the complex hardware circuit brings heavy burden of the mass and size to the limited satellite payloads [14]. An internal calibration receiver based on time division multiplexed switching (TDMS) [15] is very suitable for large-scale MBA systems. Only one element is activated at a time while the remaining ones are turned off. This procedure is repeated for each element of the array to calibrate the entire array. Since the switching time is in nanoseconds, the amplitude and phase errors are reasonably assumed to be stationary over the calibration time window.The advantage of the TDMS-based calibration receiver is that it requires only one receiving RF chain, no matter how many elements there are to be calibrated. Despite being a cost-effective implementation solution, this method suffers from the phase noise in the local oscillator [16], resulting in significant channel measurement errors [17], [18]. Characterizing how phase noise affects the calibration performance is therefore essential for practical applications. Moreover, to the best of the authors’ knowledge, previous studies lack of the theoretical analysis on the effects of the phase noise on the calibration performance. In fact,most of the calibration methods available in the literatures are under the assumption that the phase response of the oscillator is constant.This is the motivation of our work.
The rest of this paper is organized as follows. In Section II, the system model for a TDMS-based calibration integrated with the phase noise source is discussed. After that, in Section III the theoretical calibration performance is analyzed in detail. Then the theoretical computation results of different representative cases are assessed by simulations in Section IV. Finally, the conclusions are drawn in Section V.
Notation: The following notations are used throughout this paper. Boldface lowercase letters (like α ) denote vectors. The symbol [α]idenotes the i-th element of α . Superscript αTdenotes the transpose of the vector α. The notation ||x|| represents the complex modulus of a complex number x. N(µ,σ2) denotes the normal distribution with mean µ and variance σ2. Finally, the operators E(X) and var(X)represent the expectation and variance operations of the variable X, respectively.
In this paper, we analyze the impact of phase noise on the calibration performance for a MBA system.
II. SYSTEM MODEL AND PROBLEM FORMULATION
In this section, a TDMS-based calibration system model integrated with the phase noise source is explained. A MBA is de fined as an antenna capable of producing multiple spot beams simultaneously from a single aperture. Compared with the calibration for receiving array antennas, there are more challenges for trans-mitting array calibration. As shown in figure 1,a TDMS-based calibration system for transmitting multi-beam antennas consists of M beams and K antenna elements. First, M calibrating signals {cm(t)|m=1,2,…,M} enter into the M-input K-output BFN. The BFN is referred as the “heart of the MBA system” because of its ability to control the radiation pattern shape and direction. The internal structure of the M-input K-output BFN is shown in figure 2, where amkand φmkare the excitation coefficients of the attenuator and the phase shifter from the m-th input port to the k-th output port, respectively.The output signal at each channel is the sum of the M signals with attenuations and phase shifts dictated by the desired beam patterns. After the BFN, each output channel is followed by an up convertor (UC), multistage attenuators, power ampli fiers (PAs) and other RF components. In addition, an external oscillator provides clocks with the same frequency for UCs in all the RF chains. Finally, the input composite signal of the k-th antenna element of the MBA system is the sum of the M RF signals which can be described as

Fig. 1. Block diagram of a TDMS-based calibration system for transmitting MBAs.
where ftxis the carrier phase at the transmitter and cm(t ) is the m-th calibrating signal.Since all the M input calibrating signals reach an antenna element simultaneously with the same frequency, the calibration receiver must separate each calibrating signal from the composite signal. An effective separation approach is the code-division multiple access (CDMA)scheme [19], where each calibrating signal is encoded according to a unique signature code[20]. As a direct-sequence spread spectrum(DSSS) signal, the m-th calibrating signal can be formulated as [21]
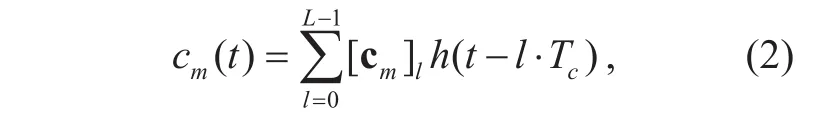
where h( t) represents the normalized rectangular pulse defined in [0,Tc), Tcis the chip duration, cmis the spreading code vector assigned to the m-th calibrating signal and the elements of the vector cmtake values of +1 or-1 with equal probability, and L is the length of cm(also known as the spreading gain). The relationship of two arbitrary code vectors satis fies the orthogonality as follows

With the fast development of MBAs to large-scale, the circuit scale of the calibration receiver increases with the number of beams and antenna elements. In order to reduce the hardware implementation cost, the designed receiver in this paper employs the TDMS measurement approach which requires only one receiving RF chain, as shown in the lower right part of figure 1. A front-end electronic single-pole multi-throw (SPMT) RF switch,controlled by the field programmable gate array (FPGA), connects a single- channel signal in turn from all the K channels. The following low noise ampli fier (LNA) ampli fies the signal of the selected channel. Then a down converter (DC) converts the RF signal to a lower intermediate frequency (IF) signal. Without loss of generality, we assume that the first channel is selected. The output noise-free IF analog signal of the DC can be represented as
试验2-40的桩土荷载分担比仅4左右,而试验2-50与试验2-60的桩土荷载分担比均近5。在荷载达到80 kPa前,桩体承担荷载比例较大,桩土荷载分担比略有上升。荷载达到80 kPa之后,由于单桩承载力有限,此时荷载继续增加,桩体承担比例降低,桩土荷载分担比降低。
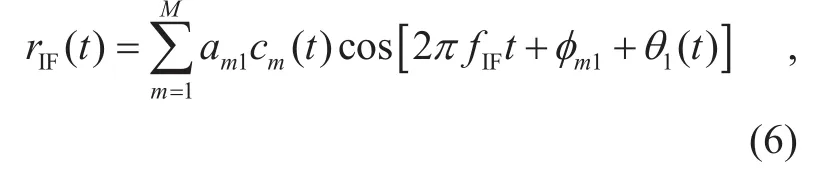
where fIFis the IF carrier frequency at the receiver and phase disturbance θ1(t) is the phase noise in the local oscillator while switching to the first channel. The phase noise is widely modeled as a zero-mean Gaussian wide-sense stationary random process [22] expressed as N(0,). In this paper, we assume that the speed of the phase noise variations is faster than the measurement time of one physical channel, thus θ1(t) affects the calibration of the channel mismatch.
The analog signal is processed by an analog-to-digital converter (ADC) and digital down converter (DDC). Since each calibrating signal corresponds to a unique signature code, K-channel parallel DMFs correlate the baseband composite signal with the following coefficients

After L⋅ Tcof time, correlation peaks appear on all the M-channel DMFs simultaneously.The peak value is the estimated complex excitation coefficient which can be written as

where xm1is the additive white Gaussian noise(AWGN) introduced by the propagation channel from the m-th beam to the first element.The real and imaginary parts of xm1,xI,m1and xQ,m1, are independent and identically distributed random variables with mean zero and variance σ2/2. From (8) we can see that the power of the useful signal is constant while the power of the noise is reduced to 1/L2. The parameter SNR is defined as the ratio of the signal power to the noise power. The SNR of the m-th calibrating signal in the first channel can be expressed as
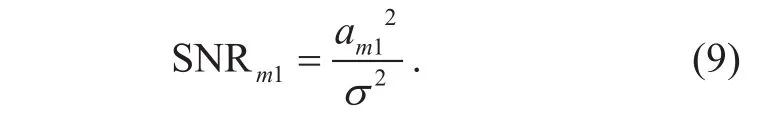
The purpose of calibration is to estimate the complex excitations (amplitude and phase) of the individual elements and to compensate for the variations between all the M input beams and K output elements [23]. Without loss of generality, we set the first calibrating signal in the first element as the reference signal. The amplitude and phase of other (M-1) signals in this element and signals in other (K-1) elements are normalized to the reference signal.The estimated amplitude in decibel (dB) and phase in degree (deg) of the m-th signal in the k-th element are

where

The subscripts I and Q represent the inphase and quadrature components of noise,respectively. For simplicity, we omit the subscript of the above variables in the following analysis.
III. THEORETICAL ANALYSIS OF CALIBRATION PERFORMANCE
The calibration performance is in fluenced by various factors, such as power level of the calibrating signal, thermal noise, phase noise introduced by the local oscillator, noise figure of the receiver, and quantization noise, etc. It is of signi ficance to derive the relationship between the calibration performance and impact factors in order to evaluate the performance of the calibration receiver. In this paper, we con-sider only the first three impact factors. Specifically, we derive the relationship between the probability of correct amplitude/phase estimation and the given tolerance region, SNR,standard deviation of phase noise.
3.1 Probability of correct amplitude estimation
Given that the tolerance region of the estimated amplitude is ±A(dB), then the probability of correct amplitude estimation in the presence of the phase noise can be replaced as follows
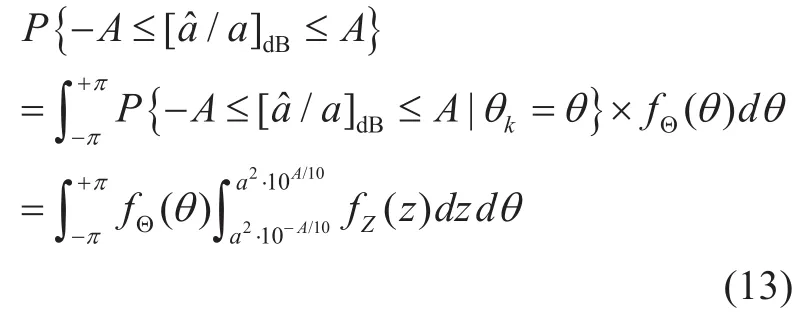

To further calculate (13), we first have to analyze the statistical characteristics of Z.According to the linear property of normal variables, the random variables Y1and Y2are distributed normally which can be written asandrespectively.Since Z is the sum of squares of two independent standard normally distributed random variables with non-zero mean,2L⋅ Z σ2has a non-central chi-squared distribution with 2 degrees of freedom and (2L⋅ a2)2σ non-centrality parameter. Referring to [24],the non-central chi-squared distribution can be approximated to a normal distribution for the large non-centrality parameter. While using the proposed calibration method, high SNR can be achieved for actual calibration systems because the transmitting signals are connected to the receiver by coaxial cables. Against this backcloth, the variable Z obeys the normal distributionapproximately. Finally, the probability of correct amplitude estimation in the presence of the phase noise can be calculated by
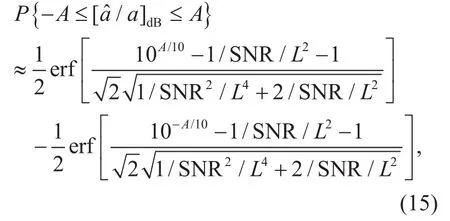
where the SNR is de fined as (9) and the error function erf(x) is de fined as
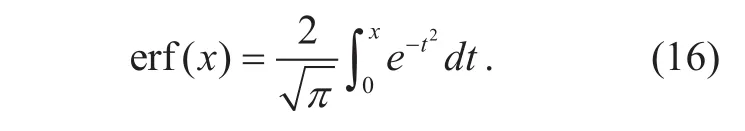
Equation (15) implies that the probability of correct amplitude estimation depends on the preset tolerance region (A), the length of the spreading code (L), and the SNR, instead of the phase noise in the local oscillator. Given the first three system parameters, the probability of correct amplitude estimation can be approximated with (15). Since calibration signals are DSSS signals, the probability of correct estimation can be improved by increasing the length of the spreading code (L) when the SNR is limited.
3.2 Probability of correct phase estimation
Given that the tolerance region of the estimated phase is ± Φ (deg) and the true phase is 0(deg), then the probability of correct phase estimation in the presence of the phase noise can be replaced as follows
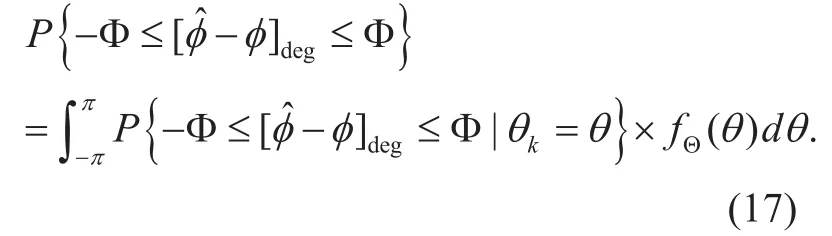
First, we analyze the statistical characteristics of Y2/Y1in (11). For a ratio of two independent normal variables, , the second-order Taylor series expansions give the following approximations [25]

Then the probability of correct phase esti-mation in the presence of the phase noise can be calculated by


In contrast to (15), the probability of correct phase estimation depends on not only the preset tolerance region (Φ), the length of the spreading code (L), and the SNR, but also the standard deviation of the phase noise.
IV. SIMULATION RESULTS
In order to con firm the validity of our theoretical analysis, three scenarios are performed in this section to compare the statistical analysis and simulation results. All calibrating signals are allocated with the equal power. In addition,the length of the spreading code (L) is selected as 256. In the following figures, blue lines are theoretical results discussed in Section III,while red lines represent Monte Carlo simulation results. Simulation results are obtained based on 10000 independent trials. In simulations, the probability of correct amplitude/phase estimation is defined as the number of trials when the amplitude/phase error is less than the tolerance region divided by the total trials.
Firstly, the approximation accuracy of the theoretical analysis is assessed by the simulations. Figure 3 shows the correct probability of the estimated amplitude versus the SNR without the phase noise. The amplitude tolerance region (A) is set as {0.05dB, 0.1dB, 0.2dB}.We can conclude that theoretical results provide exactly the same performance as simulation results. As the SNR increases, the correct probability steadily increases. In addition, better performance can be achieved obviously for larger tolerance region. Similar conclusions can also be drawn for the estimated phase as depicted in figure 4, where the phase tolerance region (Φ) is set as {0.5deg, 1deg, 2deg}.

Fig. 4. Probability of correct phase estimation versus SNR without phase noise.

Fig. 5. Probability of correct amplitude estimation versus SNR with various standard deviation of the phase noise σθ and fixed tolerance region A=0.1dB.

Fig. 6. Probability of correct phase estimation versus SNR with various standard deviation of the phase noise σθ and fixed tolerance region Φ =1deg.
Then the impact of the phase noise on the performance is taken into account. Figure 5 illustrates that the probability of correct amplitude estimation versus the SNR with the tolerance region (A) fixed to 0.1dB and the standard deviation of the phase noise (σθ) set as{0.01, 0.02}. It demonstrates that despite the presence of phase noise, the calibration performance in terms of amplitude remains unaffected. When A = 0.2dB and 0.05dB, the curves for the approximation and the simulation with various standard deviations of the phase noise are consistent. They need not be covered here.Figure 6 illustrates that the correct probability of the estimated phase versus the SNR with the tolerance region (Φ) fixed to 1deg and the standard deviation of the phase noise (σθ) set as {0.01, 0.02}. If the standard deviation of the phase noise is as large as 0.02, the correct probability of the phase is only 60% regardless of the SNR. Figure 7 further shows the upper bound of the correct probability of the estimated phase versus σθwith the SNR fixed to be 0dB and the tolerance region (Φ) set as{0.5deg, 1deg, 2deg}. When the standard deviation σθincreases, the performances of all three conditions degrade. It can also be seen that the calibration performance of the theoretical analysis is in good agreement with that of simulations.
V. CONCLUSIONS
In this paper, we present an analysis of the impact of phase noise on the calibration performance for transmitting MBA based on TDMS which achieves its advantage in implementation costs. Given speci fic system parameters,the probability of correct estimation in terms of amplitude and phase can be effectively derived. Moreover, it is concluded that the calibration performance of amplitude is independent of the phase noise while the calibration performance of the phase is sensitive to the phase noise. Finally, simulation results assess the accuracy of our theoretical analysis.
ACKNOWLEDGEMENT
This work was supported by the NSFC (Joint Foundation of NSFC & Fundamental Research for General Purpose Technologies) under Grant U1636125.
[1] M. Cheng, S. Yang, and X. Fang, "Adaptive antenna-activation based beamforming for largescale MIMO communication systems of high speed railway," China Communications, vol. 13,no. 9, 2016, pp. 12–23.
[2] J. M. Montero, A. M. Ocampo, and N. J. G.Fonseca, “C-band multiple beam antennas for communication satellites,” IEEE Transactions on Antennas and Propagation, vol. 63, no. 4, 2015,pp. 1263–1275.
[3] P. K. Bailleul, “A new era in elemental digital beamforming for spaceborne communications phased arrays,” Proceedings of the IEEE, vol. 104,no. 3, 2016, pp. 623–632.
[4] Y. Lin, X. Bu, W. Zhao, and S. Wang, “Parallel calibration method for phased array antennas with orthogonal and nonorthogonal codes,”Proc. 10th International Conference on Communications and Networking in China (ChinaCom),2015, pp. 883–886.
[5] C. M. Schmid, S. Schuster, R. Feger, and A. Stelzer,“On the eあects of calibration errors and mutual coupling on the beam pattern of an antenna array,” IEEE Transactions on Antennas and Propagation, vol. 61, no. 8, 2013, pp. 4063–4072.
[6] W. P. M. N. Keizer, “Fast and accurate array calibration using a synthetic array approach,” IEEE Transactions on Antennas and Propagation, vol.59, no. 11, 2011, pp. 4115–4122.
[7] D. Wang and Y. Wu, “Array errors active calibration algorithm based on instrumental sensors,”Science China Information Sciences, vol. 54, no.7, 2011, pp. 1500–1511.
[8] T. Takahashi, Y. Konishi, and I. Chiba, “A novel amplitude-only measurement method to determine element fields in phased arrays,” IEEE Transactions on Antennas and Propagation, vol.60, no. 7, 2012, pp. 3222–3230.
[9] H. Pawlak and A. F. Jacob, “An external calibration scheme for DBF antenna arrays,” IEEE Transactions on Antennas and Propagation, vol.58, no. 1, 2010, pp. 59–67.
[10] S. Wang, H. Qi, and W. Yu, “An internal calibration scheme for polarimetric synthetic aperture radar system,” IEEE Transactions on Geoscience and Remote Sensing, vol. 49, no. 1, 2011, pp.15–20.
[11] S. Wang, H. Qi, and W. Yu, “Polarimetric SAR internal calibration scheme based on T/R module orthogonal phase coding,” IEEE Transactions on Geoscience and Remote Sensing, vol. 47, no. 12,2009, pp. 3969–3980.
[12] L. Gao, S. Zhang, Z. Liu, J. Lin, S. Wang, and C.Xing, “An overview of multi-antenna technologies for space-ground integrated networks,”Science China Information Sciences, vol. 59, no.12, 2016, pp. 121301:1–121301:18.
[13] X. Sun, X. Yang, Z. Zeng, C. Zhang, and B. Bai, "A study on the multi-antenna geometrical depolarization channel modeling," China Communications, vol. 13, no. 3, 2016, pp. 105–114.

Fig. 7. Upper bound of the probability of correct phase estimation versus σθ with various tolerance region Φ and fixed SNR=0dB.
[14] S. Wang, J. Dai, Y. Lin, and X. Bu, “A low complexity calibration method for space-borne phased array antennas,” Proc. IEEE 83rd Vehicular Technology Conference (VTC2016-Spring),2016, pp. 1–5.
[15] D. S. Baum and H. Bolcskei, “Impact of phase noise on MIMO channel measurement accuracy,” Proc. IEEE 60th Vehicular Technology Conference (VTC2004-Fall), 2004, pp. 1614–1618.
[16] R. Krishnan, M. R. Khanzadi, N. Krishnan, Y. Wu,A. G. Amat, T. Eriksson, and R. Schober, “Linear massive MIMO precoders in the presence of phase noise—a large-scale analysis,” IEEE Transactions on Vehicular Technology, vol. 65, no. 5,2016, pp. 3057–3071.
[17] A. A. Abouda, H. M. El-Sallabi, and S. G. Haggman, “Reducing impact of phase noise on accuracy of measured MIMO channel capacity,” IEEE Antennas and Wireless Propagation Letters, vol.6, no. 11, 2007, pp. 419–422.
[18] X. Luo, X. Wang, Z. Suo, and Z. Li, “Efficient InSAR phase noise reduction via total variation regularization,” Science China Information Sciences, vol. 58, no. 8, 2015, pp. 082306:1–082306:13.
[19] M. Schwerdt, B. Brautigam, M. Bachmann, B.Doring, D. Schrank, and J. H. Gonzalez, “Final TerraSAR-X calibration results based on novel eきcient methods,” IEEE Transactions on Geoscience and Remote Sensing, vol. 48, no. 2, 2010,pp. 677–689.
[20] O. Besson, S. Bidon, and C. L. de Tournemine,“Robust approaches to remote calibration of a transmitting array,” Signal Processing, vol. 90,no. 5, 2010, pp. 1373–1381.
[21] Y. Zhang, Y. Zhuo, J. Wang, and S. Jiang, " A power reduction method for pilot channel of LEO satellite based on dynamic compensation,"China Communications, vol. 14, no. 3, 2017, pp.55–65.
[22] X. Yi, S. Hu, H. Zhou, C. Tang, B. Xu, J. Zhang,and K Qiu, “Phase noise eあ ects on phase-modulated coherent optical OFDM,” IEEE Photonics Journal, vol. 8, no. 1, 2016, pp. 1–8.
[23] H. Chou and D. Cheng, “Beam-pattern calibration in a realistic system of phased-array antennas via the implementation of a genetic algorithm with a measurement system,” IEEE Transactions on Antennas and Propagation, vol.65, no. 2, 2017, pp. 593–601.
[24] P. B. Patnaik, “The non-central 2-and F-distribution and their applications,” Biometrika, vol. 36,no. 1/2, 1949, pp. 202–232.
[25] T. Pham-Gia, N. Turkkan, and E. Marchand,“Density of the ratio of two normal random variables and applications,” Communications in Statistics, vol. 35, no. 9, 2007, pp. 1569–1591.
猜你喜欢
杂志排行
China Communications的其它文章
- Stochastic Dynamic Modeling of Rain Attenuation: A Survey
- Heuristic Solutions of Virtual Network Embedding: A Survey
- A Survey on Smart Collaborative Identi fier Networks
- Service Function Chain in Small Satellite-Based Software De fined Satellite Networks
- Coordinated Resource Allocation for Satellite-Terrestrial Coexistence Based on Radio Maps
- A Novel Roll Compensation Method for Two-Axis Transportable Satellite Antennas
