平面滚珠丝杠副多结合面建模与动态特性分析∗

2023-11-06李中凯邹光宇

振动、测试与诊断 2023年5期

李中凯，孙冉，2，邹光宇

（1.中国矿业大学机电工程学院徐州，221116）（2.徐州威卡电子控制技术有限公司徐州，221009）

引言

滚珠丝杠进给系统由于其高灵敏度、高效率、高精度等诸多优点，已成为当代进给系统中最常用的直线传动机构。然而，滚珠丝杠是一种细长、低刚度元件，在外力作用下极易产生变形、振动和噪声，这种丝杠传动系统的位置精度和稳定性通常受到机械部件结构振动模态的限制，其动态特性对设备定位精度、传动性能和故障诊断有着重要影响［1］。国内外许多学者围绕滚珠丝杠进给系统进行了动力学建模与分析。陈勇将等［2］基于丝杠滚道面力与力矩的平衡方程，推导出载荷作用下滚珠丝杠副的刚度数学模型。蒋书运等［3］借助赫兹（Hertz）接触理论计算滚珠丝杠副的结合面刚度，建立了动力学模型，并基于有限元法分析该模型的动态特性。杨勇等［4］基于铁木辛柯梁假设，考虑丝杠轴的横向剪切，建立丝杠与工作台系统动力学模型。朱坚民等［5］建立进给系统结合面等效弹簧的有限元模型，讨论了机械结构参数变化对进给系统动态特性的影响。现有研究方法虽然较好地分析了滚珠丝杠副动态特性，但还存在一些不足，例如：结合面接触刚度考虑不充分，有限元建模时简化较大，没有模态试验佐证理论模型或没有对之前的试验结果对比分析等。针对上述问题，笔者以x-y平面滚珠丝杠副为研究对象，基于吉村允孝法和Hertz 接触理论计算结合面刚度，忽略阻尼对固有频率的微小影响，使用等效弹簧单元将模型简化，建立进给系统的多结合面动力学模型。进一步根据有限元法、对比研究和应用研究，验证了所建立模型的正确性。

1 进给系统动态建模

图1 所示为带滚珠丝杠副的x-y轴进给系统结构，通过滚珠丝杠副和直线导轨副的组合实现工作台x-y方向的进给。其中：S为滑块间距；D1为下导轨间距；D2为上导轨间距。S，D1，D2与系统总质量M，共同构成平面滚珠丝杠副的主要可调节参数。

图1 x-y 轴进给系统结构示意Fig.1 Structure of x-y axis feeding system

1.1 固定结合面接触刚度与等效弹簧单元

固定结合面接触压力源于其上结构部件的重力和螺栓联结的预紧力，预紧力的大小取决于螺栓组的强度和联结要求。螺栓设计的原则是保证所要求的预紧力，并且连接的结构尺寸不宜过大。螺栓预紧力的推荐值为

其中：σL为螺栓材料屈服点；，为螺栓应力截面积，dL为螺纹的基本小径。

平均接触压力为

其中：n为结合面联结螺栓数量；M为结合面承受结构部件重力；A为实际结合面积。

运用吉村允孝法［6］可以计算出固定结合面之间的参数，假设接触面上任意无穷小接触面为N，接触面积为dxdy，其上所受压力可认为均布为P，则接触面N上动态特性等效刚度参数值为

其中：k1，k2分别为结合面相应等效参数系数，可根据压力P查到［7］；A为结合面的面积。

每个固定结合部采用4 组并联弹簧单元将两接触面相连。

1.2 滚动结合面接触刚度与等效弹簧单元

滚珠丝杠副在外载荷作用下，滚珠与接触面发生弹性变形，此时在压力作用下形成的接触变形可看作两曲面的点接触形式。基于Hertz 接触理论［8］探究平面进给系统滚动结合面的受力方向与受力类型，将其等效为接触面弹簧单元。点接触的两物体，在负载Q的作用下，由Hertz 理论得

接触刚度为

其中：K，a为Hertz 接触系数，与主曲率函数F(ρ)的值有关，可在文献［9］中查到；u1，u2为泊松比；E1，E2为弹性模量；ρ为接触处主曲率。

1.2.1 单螺母组件接触刚度与等效弹簧单元

滚珠丝杠受力与变形如图2 所示。由图2（a）可知，滚珠与丝杠滚道面、螺母滚道面的接触点分别为S和N，满足Hertz 接触理论的假设条件。根据静力学平衡，当螺母受载荷作用力F时，假设法向力大小为P，接触角为β，螺旋角为λ，根据滚珠受力均等，得

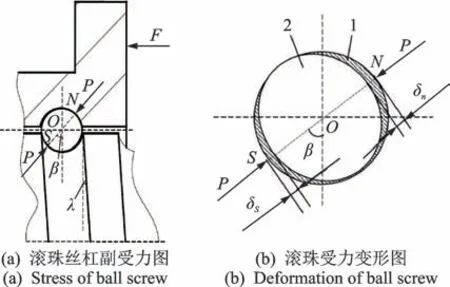
图2 滚珠丝杠受力与变形图Fig.2 Stress and deformation diagram of ball screw

在法向力P的作用下，滚珠与丝杠滚道面、螺母滚道面接触点所产生的位移如图2（b）所示，则轴向总变形量δL与径向变形量δJ分别为

对于滚珠丝杠副而言，滚珠与丝杠滚道面、螺母滚道面接触处的主曲率和分别为

其中：r为单个滚珠直径；t为滚道曲率比；d为滚珠丝杠直径。

根据文献［10］，取滚珠丝杠螺母承受轴向载荷为12.75 kN，径向载荷为0.436 kN，由式（7）得其轴向刚度与径向刚度。考虑到丝杠螺母有3 列滚珠环绕，因此用3 个截面等效，则丝杠螺母轴向和径向均匀分布6×3 根等效弹簧单元将丝杠与螺母相连，每个弹簧单元的刚度为结合部刚度的1/18。

1.2.2 轴承的接触刚度与等效弹簧单元

在滚珠丝杠进给系统中，固定端采用成对角接触轴承串联安装方式，支撑端采用单个角接触轴承。

1）单轴承刚度计算。假设轴承轴向预紧力为Fa，根据单个轴承水平方向受力平衡，各滚珠法向接触载荷为

轴承径向受力，相邻两滚珠夹角为ψ，轴向预紧力Fa作用下，滚珠的等效径向作用为FJ。根据竖直方向受力平衡，得各滚珠径向接触载荷为

滚珠与外圈滚道面、内圈滚道面接触点所产生的接触变形δS，δN如式（9）和式（10）所示，得出滚珠与轴承内外接触面的变形量为

其中：kn为轴承接触变形常数。

查阅轴承相关参数，根据式（7）和式（15）可得载荷作用下轴向位移和轴向刚度。

2）配对轴承刚度计算。配对轴承串联安装，两轴加载预紧力为F，轴承的形变量为δa。当在轴承I上作用轴向力Fa时，产生轴向变形δx，此时轴承Ⅰ，Ⅱ总的轴向变形量和总的轴向载荷为

由式（19）可得F1和F2，根据力平衡条件得

当配对角接触轴同时承受轴向预紧力F和径向力Fr时，轴承外圈中线相对内圈中心，在轴向和径向相对平移了δx和δr，轴承内圈滚道上距离最大载荷滚珠ψ处相对轴承外圈的最大形变量为

由式（15）可得

根据径向力平衡条件可得

根据式（7）可得配对轴承轴向刚度和径向刚度。考虑到单轴承有1 列滚珠，用1 个截面等效。丝杠和轴承结合部均匀分布4 根等效弹簧单元，将丝杠与轴承相连，每个弹簧单元刚度为结合部轴向刚度和径向刚度的1/4，配对轴承有2 列滚珠，用2 个截面等效。丝杠和轴承结合部均匀分布4×2 根等效弹簧单元将丝杠与轴承相连，每个弹簧单元刚度为结合面轴向与径向刚度的1/8。轴承弹簧单元模型如图3 所示。

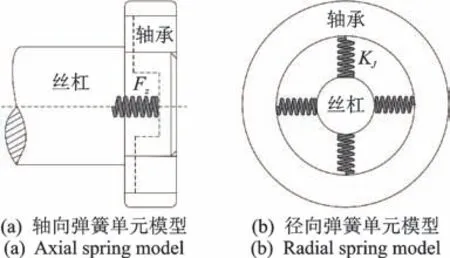
图3 轴承弹簧单元模型Fig.3 Bearing spring unit model

1.2.3 导轨副结合面建模及其特性参数获取

导轨副弹簧单元模型如图4 所示。由图4（a）可知，滑块受到力Fn作用，各滚珠的受力分别为F1，F2，F3和F4，其中：F1=F2；F3=F4；α为滚珠与滚道面间的接触角。由静力平衡条件得

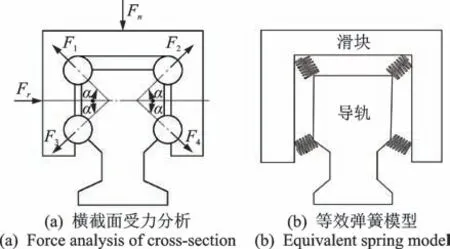
图4 导轨副弹簧单元模型Fig.4 Guide rail pair spring unit model

由Hertz 接触理论与力学叠加原理得

其中：n为单列滚道的滚珠数；F0为预紧力作用下单个滚珠的法向力。

在预压载荷Fn作用下，上排滚珠的变形量为δs，下排滚珠的变形量为δn，滑块在竖直方向的位移为δv，由变形协调方程得

由式（27）可得单个滚珠在预紧力作用下的初始变形量δ0。滚珠与导轨滚道面、滑块滚道面接触处的主曲率和分别为∑Ps和∑Pn，由式（11）、式（12）可计算其值。滚珠与滚道面接触处的4 个主曲率中，ρ22的值应为0，继而求得δs和δn。

根据已知参数与公式，导轨副结合部的法向刚度为

滚动导轨副结合部的切向刚度为

根据滚动导轨副相关计算参数，由式（29）可得其结合面刚度计算的结果。因此，滚动导轨副均匀分布4 根等效弹簧单元将滑块与导轨相连，每个弹簧单元的法向刚度与切向刚度分别为结合部刚度的1/4，如图4（b）所示。

2 物理试验验证

2.1 有限元建模与模态分析

根据上面提出的弹簧单元模型，将滚珠丝杠进给系统在ABAQUS 软件中设置面与面的接触，将结合面看作是中间有弹簧连接。仿真弹簧单元参数设置数据来源于上述关于结合面接触刚度的计算，不同物体在接触时都不是完全固定住的，其联结强度取决于结合面上的压力与螺栓预紧力。分布压力与螺栓预紧力越大，计算的弹簧接触刚度也越大，连接的越紧固；结合面刚度越大，则有限元仿真模型的固有频率越大。在ABAQUS 中使用Complete analysis 提交作业，对模型进行模态分析，进给系统理论模态分析结果如表1 所示（以图1 坐标系为参考）。

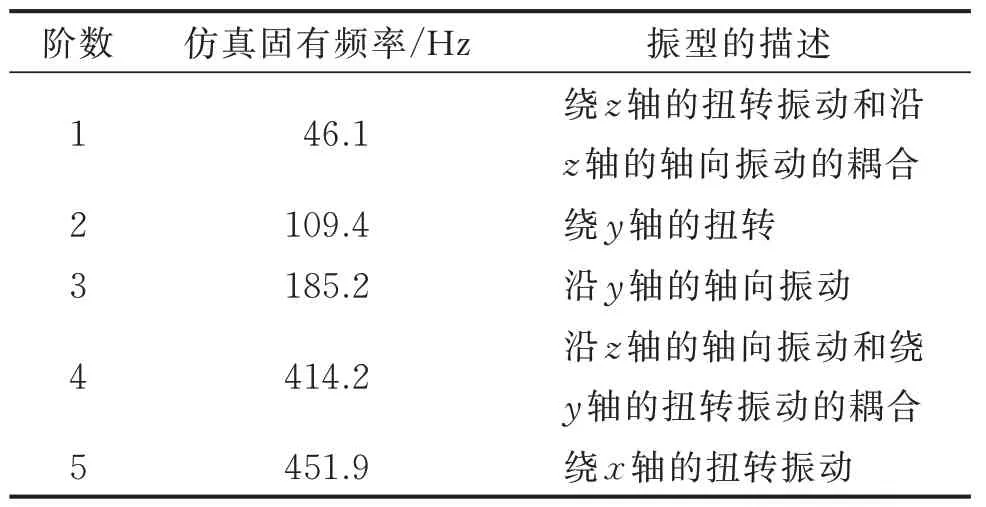
表1 进给系统理论模态分析结果Tab.1 Theoretical modal analysis results of feed system

2.2 模态试验验证

对滚珠丝杠进给系统进行模态试验，现场试验如图5 所示，使用的测试系统主要有LC02 型力锤、1A116E 型和1A108 型IEPE 压电式单向加速度传感器、DH59220D 动态数据采集仪和DHDAS 动态信号模态分析系统。

图5 现场试验图Fig.5 Field test diagram

采用冲击锤单点激励法，试验选用单自由度传感器，布置了52 个测试点，共测得390 个频响函数，经过重复分析计算，最终建立的试验稳态图如图6所示。

图6 试验稳态图Fig.6 Test steady state diagram

模态仿真与试验结果对比如表2 所示。为了进一步验证误差结果的可靠性，分别建立集中质量与反向间隙+动态特性响应试验（方法1［11］）、分形理论与Hertz 理论+模态试验（方法2［12］）以及Hertz 理论、吉村允效法+模态试验（方法3，即本研究方法），不同方法对结合面理论模型验证方案对比如表3 所示。通过分析发现，文献［11］运用集中质量建模与反向间隙研究固有频率误差偏小，分形理论+Hertz 理论研究［12］与Hertz 理论+吉村允效法对比结果较近，但由于方法1 与方法2 计算模型非常小，所以方法3 的结合面刚度计算误差较小，对几何模型的简化效果较好。

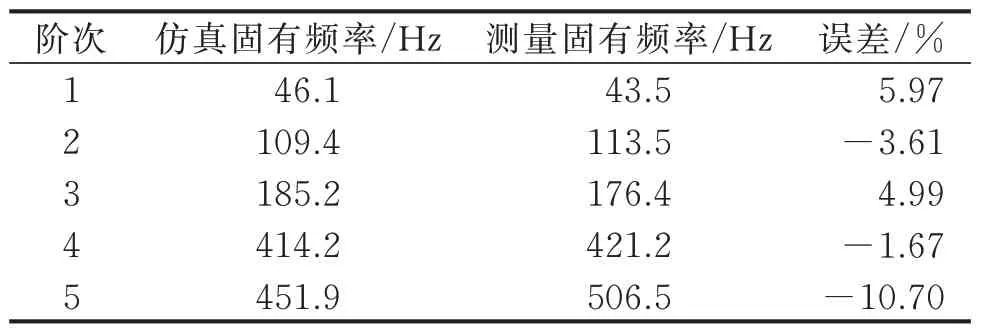
表2 模态仿真与试验结果对比Tab.2 Comparison of modal simulation and test results

表3 不同方法对结合面理论模型验证方案对比Tab.3 Comparison of verification schemes of theoretical model of joint surface by different methods

仿真与试验模态振型对比如图7 所示，可以看出，每阶理论模态振型与对应仿真模态振型沿固定方向的扭转与振动基本一致，为研究进给系统动态特性影响因素提供了基础。

图7 仿真与试验模态振型对比图Fig.7 Comparison between simulation and test modes

3 动态特性影响因素

3.1 工作台质量的影响

工作台的位置见图1，保持其他参数不变，在ABAQUS 中分别计算不同工作台质量下对应的各阶固有频率。工作台质量的影响如图8 所示。

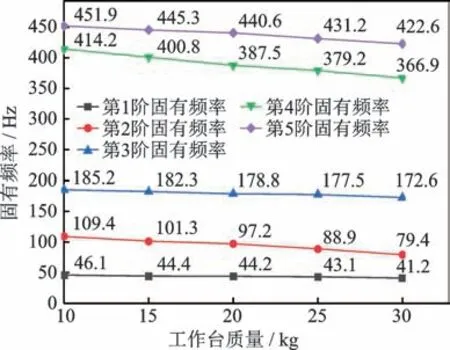
图8 工作台质量的影响Fig.8 The influence of workbench mass

可以看出，各阶频率随着工作台质量的增大而下降。第1，3 阶固有频率受工作台质量的影响较小，而第2，4，5 阶受工作台质量的影响较大。这是由于固有频率正比于，各阶频率下降的快慢反映了工作台质量对各阶频率值影响的权重。

3.2 滑块间距的影响

设置滑块间距离为S（40～120 mm），其他参数不变，在ABAQUS 中分别计算不同间距下的各阶固有频率变化，滑块间距的影响如图9 所示。在滑块间距变化的过程中，第1，3，4 阶固有频率基本保持不变，而第2，5 阶固有频率随着滑块间距的增大明显上升。第1 阶振型为绕z轴的扭转振动和沿z轴的轴向振动的耦合，第3 阶振型为沿y轴的轴向振动，第4 阶振型为沿z轴的轴向振动和绕y轴的扭转振动的耦合，这3 阶振型受滑块间距影响较小，所以固有频率变化很小。当滑块间距小于40 mm 时，每阶固有频率变化与上述规律一致，当滑块间距大于120 mm 时，受到底板和连接板尺寸的制约，其固有频率变化需重新分析有限元模型。

图9 滑块间距的影响Fig.9 The influence of the distance between sliders

3.3 导轨间距的影响

设置下导轨的间距为D1，上导轨的间距为D2，其他参数不变，在ABAQUS 中分别计算上下导轨间距变化对各阶固有频率的影响。导轨间距D1变化的影响如图10 所示，由图可知，增大导轨间距D1，系统第1，3 阶固有频率上升较快，而第2，4，5 阶频率基本保持不变。这是由于导轨间距D1影响绕z轴扭转刚度，同时间距增大使得进给系统y轴的轴向刚度增大，所以第1，3 阶固有频率变化显著，而对x和y轴扭转以及z轴轴向位移影响较小，所以第2，4，5 阶固有频率变化曲线平直。

图10 导轨间距D1变化的影响Fig.10 The influence of the change of the distance between guide rails D1

增大导轨间距D2，系统第2，4 阶固有频率上升较大，而第1，3，5 阶频率基本保持不变。这是由于导轨间距D2影响绕y轴的扭转，所以第2，4 阶频率变化显著，而对x和z轴的扭转以及y轴的轴向位移影响较小，所以第1，3，5 阶固有频率变化较小。

3.4 结果分析

1）进给系统第1，3 阶振型为丝杠的弯曲形变，对其固有频率影响最大的是导轨间距D1，增大D1能有效地提高其固有频率，工作台质量对其有影响，而滑块间距S和导轨间距D2对其影响甚微。

2）进给系统第2 阶振型为绕y轴的扭转，工作台质量、滑块间距S和导轨间距D2对其影响很大，减小工作台的质量，增大S与D2均能有效地提高其固有频率。

3）进给系统第4 阶振型为沿z轴的轴向振动和绕y轴的扭转振动的耦合，工作台质量和导轨间距D2对其影响很大，减小工作台的质量，增大D2均能有效地提高其固有频率。

为满足结构运行尺寸需要，避免结构共振情况，保证系统运行稳定性，给出进给系统结构设计范围值如表4 所示。

表4 进给系统结构设计建议值Tab.4 Suggested values for the structure design of the feed system

3.5 实例验证

笔者设计了医用剪刀毛坯上料设备，根据以上模态分析与动态特性影响因素的研究，因各阶固有频率随着工作台质量的增大而下降，应尽量使工作台质量小一些，同时还需要考虑承载件规格与结构稳定性。因滑块间距S的变化对系统1，3，4 阶固有频率影响甚小，在滑块间距设计时应考虑配合构件尺寸与空间利用率。因导轨间距D1增大时，系统第1，3 阶固有频率上升较快，设计时应尽量使D1大一些，同时要考虑工作现场的尺寸范围与结构构件之间的配合。导轨间距D2变化时，系统第1，3，5 阶固有频率影响相对较小，设计D2时应考虑协同配件规格与空间的合理利用。

优化平面进给系统设计尺寸和设法减小结构的质量，拟定平面进给系统设计参数如表5 所示。交流伺服电机的固有频率为50 Hz，前文已使用锤击法依据此进给系统验证了有限元模型的正确性，即验证了本研究给出的工作台质量、滑块间距及导轨间距等的建议值。采用双滚珠丝杠副平面进给系统改变物体输送轨迹，将其从初始位置放置到目标位置，现场试验测试如图11 所示。丝杠运行速度为200～600 mm/s，经过150 次反复试验，没有出现位置偏差与结构共振，且保持运行平稳、高效率和低噪声，满足高质量、高可靠性和低成本的设计要求。