寒区高边坡机场坡顶土体振动响应研究∗

2023-11-06刘国光裴磊洋牛富俊

振动、测试与诊断 2023年5期

刘国光，裴磊洋，牛富俊

（1.中国民航大学交通科学与工程学院天津，300300）（2.中国科学院西北生态环境资源研究院冻土工程国家重点实验室兰州，730000）（3.中国科学院大学北京，100039）（4.中山大学土木工程学院广州，510275）

引言

高填方机场广泛存在于我国西部、北部等非平原地区，受场地条件及工程成本限制，高填方机场需要尽可能缩小跑道端净空区及两侧内水平面的土面区面积。由于飞机起降、滑跑和制动过程中与边坡距离较近，与跑道相互作用产生的振动给边坡动力稳定性造成了严重影响［1］。此外，为避免飞机迫降土面区时起落架折断造成机身损坏，需要定期对土面区进行振动碾压作业。该特殊工况对坡顶边缘土体产生了推挤作用，进一步降低了高边坡的稳定性。尤其是位于寒区的高填方机场，冻融作用造成的表层土体松散、孔隙率上升和含水量变化，造成边坡不同程度的变形、失稳和塌陷等工程病害［2］。

边坡变形主要表现为松动和蠕动两大类。松动往往是由外界荷载作用产生的松动裂隙所引起；蠕动则为土体在自重作用下缓慢而持续的变形。针对边坡长期蠕动破坏已开展了深入研究，提出了许多本构模型，并成功应用于反演坡体力学参数及预测后期沉降［3-4］。然而，寒区高填方机场坡顶振动破坏现象属于短期边坡松动问题。

现场试验和室内模型试验是研究冻融作用对冻结土体力学性能影响的重要手段［5-7］。试验结果表明，含冰量和温度是影响冻土力学性能最重要的内因和外因［1］。温度代表了土体的冻结程度，在与含冰量之间存在指数函数关系的同时，还与冻胀破坏造成的土体松散效果紧密相关［8］。在春融阶段，冻结土体的本构关系由广义双曲线模型变为邓肯-张模型，冻土强度折减系数也随之变化［9］。边坡水-热-力耦合数值模型从冻融循环角度成功解释了温度对边坡松动的不利影响，5 次冻融循环后边坡的安全系数下降近10%［10］。应力-渗流-温度三场耦合模型指出，边坡浅层土体的冻结状态变化对边坡稳定性有较大影响［11］。冻融作用对土体力学性能的复杂影响说明，春融阶段虽然只是寒区机场飞行区管理过程中的一个特殊时期，但对高边坡稳定性的影响却不容忽视。

除冻融循环外，外部荷载的动力作用也是造成寒区边坡工程破坏的重要因素［12］。当考虑地震荷载作用并结合缩尺振动台模型试验发现，小震下边坡稳定性问题和其动力性能随着边坡物理性质改变而变化，在地震作用下边坡动力响应存在放大效应［13］。有限元分析结果表明，该放大系数随高度增大而增大，坡顶处放大系数最大为2.44～3.8［14］。寒区高填方机场边坡长期经受冻融循环、飞机及重型碾压设备的共同作用，边坡动力响应变化规律更复杂。尤其是春融季节，边坡顶部表层土体从完全冻结状态转化为融化状态，更易在外界动荷载扰动下加剧坡顶边缘无约束土体松动乃至发生局部破坏。

笔者通过室内振动台试验，采集了升温过程中冻结土样的温度场及加速度时程数据，分析了时域和频域内土样动力性能随土样松散程度的变化规律，并对振动台试验的响应加速度数据进行了包括时域和频域在内的精细分析，提出了无约束冻结土样动力响应的力学计算模型，总结了升温过程中的冻结土样动力响应特征随冻结状况的变化规律，为寒区高填方机场坡顶边缘土体稳定性评价及预测提供了新方法。

1 高填方机场坡顶土体动力响应计算模型

某高边坡机场坡顶土体局部滑动如图1所示，该机场使用5年后首次出现了坡顶边缘土体失稳滑动，造成支护结构失稳和围界倒塌。经调查发现：该区域土体松动、支护结构存在水平变形，是病害产生的内因；连续降雨造成土体含水率增加，是病害产生的外因；飞机及碾压设备的振动作用，是病害产生的扰动因素。

图1 某高边坡机场坡顶土体局部滑动Fig.1 Top soil slide on the high-filled slope of an airport

以滑坡区域土体为研究对象，可知土体松动后将处于无约束（或弱约束）状态，其对外界振动作用的动力响应可采用图2 所示的无约束土体水平振动计算模型进行分析。假设将表层土体在深度方向分成n层带质量和阻尼的弹簧单元，每个单元同相邻上下层的单元并联，动力作用逐层传递并衰减。当振源来自表层时，顶部单元受到振动作用影响最大，随着深度的增加，响应变小；当振源来自底部时，视能量大小将诱发模型上部部分弹簧的关联振动。

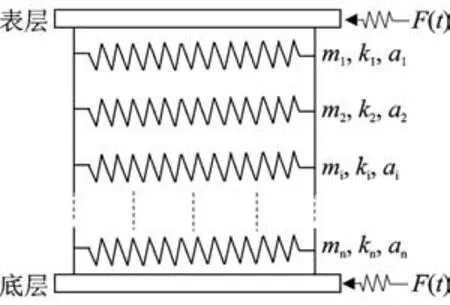
图2 无约束土体水平振动计算模型Fig.2 Calculation model of unconstrained soil under horizontal vibration

假设底部第n层弹簧单元受到外力Fn(t)的激励作用，传递到第j层的力为Fj(t)（1 ≤i≤j≤n）。考虑阻尼作用，Fj(t)将随着j的减小而逐渐降低，直至为0，则可建立弹簧单元的振动方程为

其中：mj，kj和cj分别为弹簧单元j的质量系数、刚度系数和阻尼系数，1 ≤i≤j≤n；xj为弹簧单元j的水平位移值。

取第j层弹簧单元进行振动分析，振动方程为

利用Duhamel 积分原理，假设Fj(t) 遵从Fj(t)=ajt+bj衰减规律，则式（2）的理论解为

将弹簧单元的已知条件带入式（3）中，采用Matlab 进行计算可知：假设融化过程中的弹簧单元阻尼cj变化不大，当弹簧单元刚度kj变大，其动变形量xj变小，土体松散程度变低。通过监测动荷载作用下边坡顶部边缘土体的动变形量计算得到kj，即可评价土体松散程度和预测边坡稳定性。对于存在冻融破坏现象的寒区机场高边坡，冬季冻结期土体松散程度降低，春融期土体松散程度上升，使得kj发生显著的周期性变化。

2 室内土样模型振动台试验

2.1 冻结土样制备

某寒区高填方机场边坡土体物理指标如表1 所示，现场取土后于室内制作了质量含水率分别为5%和10%、压实度为95%及边长为0.27 m 的立方体冻结土样，其制备过程如图3 所示。2 个加速度传感器分别预埋在土样底部和中部，用于记录振动台试验中土样底部和中部的加速度变化，同时等间距分层预埋4 个温度传感器记录土样的温度变化。土样经分层填充手动压实后，在-10 °C 的冷冻箱中养护7 d 后在环境温度15 ℃下进行自然升温状况下的振动台试验。

表1 某寒区高填方机场边坡土体物理指标Tab.1 Physical properties of top soil on the highfilled slope of cold region airport

图3 冻结土样制备Fig.3 Preparation of frozen soil models

2.2 振动台试验相关参数

根据飞机滑行状态下道面振动响应的现场实测数据可知，道面最大响应加速度为0.1 m/s2，响应频率为5 Hz［15］。考虑振动沿土面区传递后的能量衰减，设实验室振动台激振器的输入随机激振信号频率为5 Hz，最大加速度为0.06 m/s2。试验准备工作结束后，室内振动台试验测得的加速度时程曲线如图4 所示。

图4 室内振动台试验测得的加速度时程曲线Fig.4 Measured acceleration curves of shaking-table test

2.3 振动台试验测试结果

图5 为振动台试验期间同步记录的不同质量含水率的冻结土样温度和响应加速度时程曲线。为更精细地分阶段研究升温过程中冻结土样动力响应变化规律，根据土样冻结状态和土样典型位置的温度临界值，将升温过程中的土样温度变化曲线划分为4 个阶段［16］：土样表面温度低于-1 °C 的低温冻结阶段（阶段1）；土样表面温度在-1～0 °C 之间的高温冻结阶段（阶段2）；土样表面温度高于0 °C 但中心温度低于0 °C 的局部融化阶段（阶段3）；土样中心温度高于0 °C 的完全融化阶段（阶段4）。不同的冻结状态代表着土样在冰的胶结作用下与其动力响应密切相关的松散度和完整性。

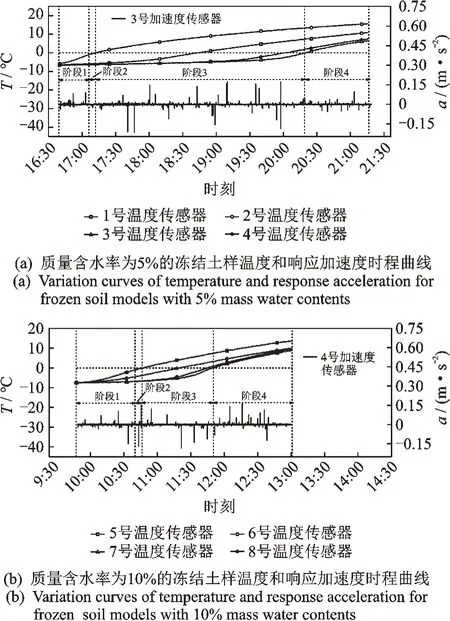
图5 不同质量含水率的冻结土样温度和响应加速度时程曲线Fig.5 Variation curves of temperature and response acceleration for frozen soil models with different mass water contents

由图5 可知，不同含水率的冻结土样升温趋势总体接近，但含水量越高局部融化阶段持续时间越短。加速度响应随着土样融化呈现从小幅波动到剧烈波动的变化趋势，动力放大系数分别为1.00～3.34（质量含水率为5%）和1.00～3.12（质量含水率为10%），表明含水率对冻结土样的加速度响应存在一定影响。

3 不同冻结状况对土样振动响应的影响

3.1 冻结状况对加速度变化率的影响

为更有效地研究升温过程中冻结土样振动响应的变化规律，定义Ra来比较不同冻结状况下响应加速度的变化特征［17］，即

其中：ai为土样i时刻的响应加速度值；aj为土样j时刻的响应加速度值。

不同质量含水率的冻结土样Ra变化曲线如图6所示，可知升温过程中冻结土样Ra发生显著变化，但局部融化阶段的Ra变化幅值最大。对比图6（a）和（b）可知，随着含水率增加，第3 阶段的Ra变化幅度加大，对土样振动响应产生了明显影响。

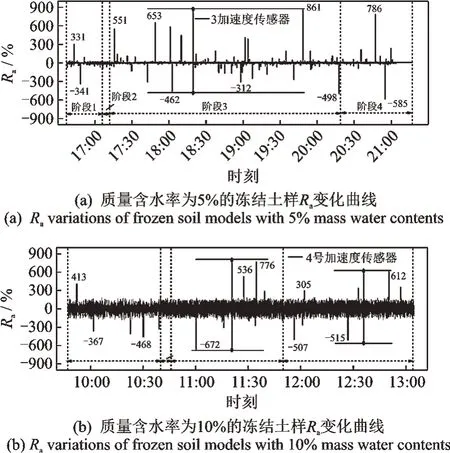
图6 不同质量含水率的冻结土样Ra变化曲线Fig.6 Variations of Ra in frozen soil models with different mass water contents

为进一步分析冻结土样振动响应的变化规律，通过缩小时间窗方式对图5 所示加速度时程曲线进行分析。定义试验过程中每15 min 内Ra绝对值大于75%的数量为（无量纲），可得到不同质量含水率的冻结土样变化趋势如图7 所示。由图可知，在高温冻结阶段开始波动并在局部融化阶段达到峰值。当含水率由5%增加到10%时，由波动变化变为近似服从正态分布，的均值由2.2 增加到4.2，说明土样振动响应随着含水率的增加而加大，并且规律性更加明显。

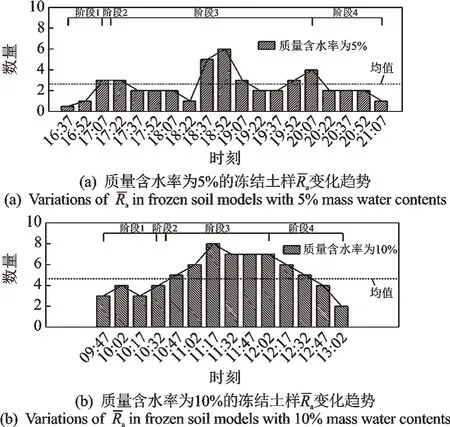
图7 不同质量含水率的冻结土样变化趋势Fig.7 Variations of in frozen soil models with different mass water contents

3.2 冻结状况对土样振动频率的影响

由傅里叶理论可知，所有的波都可以通过FFT分解成不同形式的正弦波。因此，可通过功率谱密度（power spectral density，简称PSD）研究频域中受升温作用影响的冻结土样振动响应变化规律。PSD分析中的自相关算法为

其中：f(t)为信号函数；R(τ)为信号函数的自相关函数；T为信号函数的周期。

由Wiener-Khinchin 理论可知，获得的自相关函数需要用FFT 进行分析处理［18］，即

其中：rxx(τ)为定义在数学期望下的自相关函数；i 为虚数单位；Sxx(f)为信号函数的功率谱密度函数。

通过式（8）可实现连续随机变化的加速度信号分析

其中：FT(ω)为被周期T截断的信号谱函数；p(ω)为信号函数的功率谱密度函数。

在图5 中每间隔20 min 截取1 组加速度数据导入Matlab 进行PSD 分析，质量含水率为5%和10%的冻结土样的PSD 分析结果分别如图8，9 所示。冻结土样的响应频率随着冻结状况不断变化，完全冻结阶段土样响应频率与输入频率相同（5 Hz），完全融化后土样响应频率增长到7 Hz 左右。

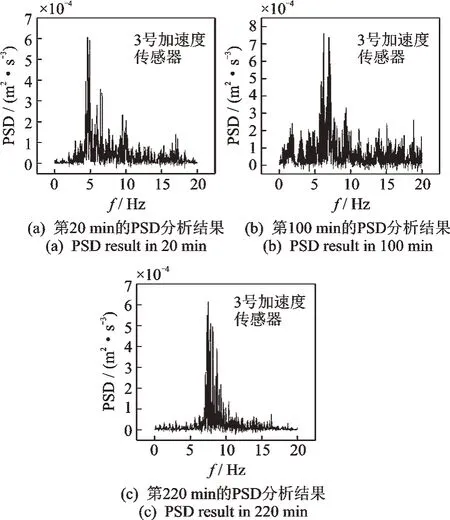
图8 质量含水率为5%的冻结土样的PSD 分析结果Fig.8 PSD analysis results of the frozen soil models with 5% mass water contents

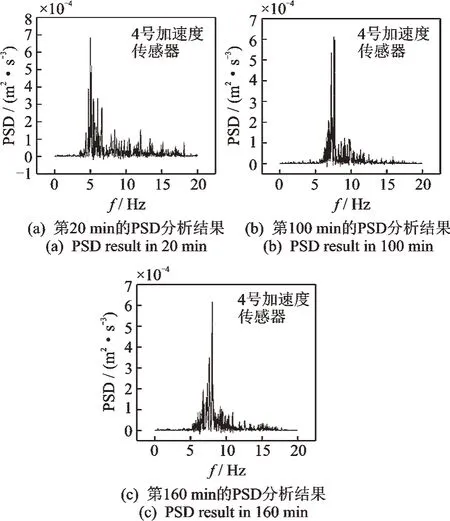
图9 质量含水率为10%的冻结土样的PSD 分析结果Fig.9 PSD analysis results of the frozen soil models with 10% mass water contents

为精确获得升温作用对冻结土样振动响应的影响，采用缩小取样间隔的方法重复上述过程。每6 min 提取1 组加速度数据进行PSD 分析，得到对应频率变化的散点图及拟合曲线，不同质量含水率的冻结土样频域响应特征曲线如图10所示。同时，定义Rf来分析升温作用对土样振动响应频率的影响，即

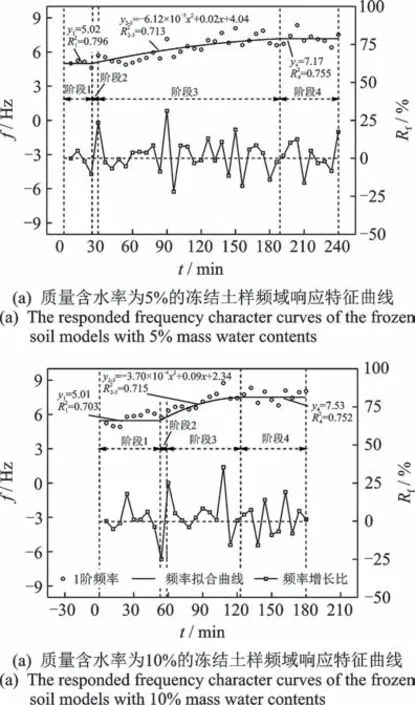
图10 不同质量含水率的冻结土样频域响应特征曲线Fig.10 The responded frequency character curves of the frozen soil models with different mass water contents

其中：bi为土样i时刻的响应频率；bj为土样j时刻的响应频率。

根据冻结状态不同，对图10 中冻结土样响应频率进行分阶段拟合。由图可见：不同含水率的冻结土样在完全冻结阶段和完全融化阶段响应频率变化近似直线；在高温冻结和部分融化阶段响应频率变化接近二次曲线；在4 个阶段的均方差R2均大于0.7，表明拟合曲线具有较高的可靠性。随着含水率增加，在部分融化阶段响应频率的增加速率也明显增大，Rf最大值从30.5%增加到35.4%，完全融化后的响应频率值也由7.13 Hz增加到7.53 Hz，与笔者提出的坡顶边缘土体动力响应计算模型分析结果一致。此外，在不同含水率时Rf均在第2 阶段首次出现了显著波动，均在第3 阶段达到峰值，说明土样振动响应性能变化发生在加速度变化规律尚不显著的高温冻结阶段。因此，相较于时域分析结果，在频域内分析冻结土体的振动响应特征更有效。

3.3 基于响应频率的坡顶土体稳定性评价

升温过程中，冻结土样中心部位由完全冻结状态转变为完全融化状态。在完全冻结状态，各层弹簧单元的kj相同，因而冻结土样中心位置响应频率与底部输入频率一致。当土样处于部分融化状态时，土体弹性变形能力逐渐恢复，土样中心位置下部各弹簧单元产生并联振动。假设此时总体刚度为K，则。当i越小，即计算位置距离振动台顶面越远时，K越小。因此，当冻结土样开始融化时，中心位置振动频率增加，体现了振动响应的动态放大效应。当土样完全融化后，土样动力响应频率达到极值并基本保持稳定，该频率极值体现了冻融作用影响后土体的松散度。部分融化土样表面裂隙状况如图11 所示，由图可知，在相同初始压实度情况下，含水率越高，冻胀对土体的完整性破坏作用越强，土样松散度越大。完全融化后土体的振动响应频率越大，越容易造成高填方坡顶边缘位置土体稳定性下降，从而在外荷载扰动下易诱发局部失稳破坏。因此，可通过在高填方坡顶边缘浅层埋设加速度传感器采集飞机或土面区碾压机械工作时引起的土体振动响应，根据响应频率的变化进行土体松散度评价和稳定性监测。