多尺度卷积神经网络小样本轴承故障辨识方法∗

邢自扬，赵荣珍，吴耀春，何天经

（兰州理工大学机电工程学院 兰州，730050）

引言

旋转机械在现代工业中发挥着重要作用，而滚动轴承作为其中关键支撑零部件，一旦发生故障将会导致灾难性事故。因此，对滚动轴承进行故障辨识研究具有重要的现实意义［1］。

目前，智能故障辨识方法主要分为传统算法与深度学习算法。传统算法包含特征提取、特征选择及模式识别等过程，存在效率较低、最终结果受特征质量影响较大等不足［2］。深度学习克服了传统方法的缺点，能够自动挖掘数据中的抽象敏感特征信息［3］。卷积神经网络（convolutional neural network，简称CNN）作为深度学习中极具代表性的算法，由于其出色的特征自学习能力，已经成功应用于故障辨识领域［4］。

振动信号中通常耦合不同的分量，包含多个固有振动模态，因此表现出多尺度特性，在不同的时间尺度上包含复杂的模式。传统的CNN 没有考虑数据中内在的多尺度特性，一些学者从多尺度角度出发提取数据中的特征，准确地完成故障诊断［5］。以上方法在实际应用中存在以下问题：①现场故障数据难以获取且代价昂贵，少量训练样本难以实现高精度故障辨识；②设备的环境噪声对于故障辨识准确率影响较大［6］。如何解决这些问题成为有效利用人工智能完成实际生产应用中的关键，是当前工业人工智能研究的热点问题之一［7］。

针对小样本问题，常用的方法有扩充目标样本数量与迁移学习［8］。前者通常采用生成模型来扩充样本的数量［9］，然而该方法难以衡量生成样本的准确性与多样性；后者通过迁移学习的方式，将从大型数据集中学习得到的知识应用于小样本的目标域，从而实现小样本故障辨识［10］，但是源域和目标域之间的分布差异难以衡量，存在负迁移的现象。

针对模型的抗噪性，一些学者从数据和算法两方面提出了具有抗噪能力的深度学习故障诊断模型，但是其性能仍有进一步挖掘的潜力［6］。

不论是小样本还是模型的抗噪性问题，都可以归因于训练样本与测试样本特征的分布存在差异［11］。文献［12］指出，批标准化技术（batch normalization，简称BN）可以减小训练样本与测试样本特征之间的分布差异，但BN 的计算结果受训练批次大小的影响，且BN 在测试阶段仍采用训练样本的均值与方差，因此在训练样本与测试样本的分布存在差异的情况下，BN 不能很好地满足要求。针对这些不足，Ulyanov 等［13］提出IN，仅针对单个样本的单个特征通道进行归一化，克服了BN 的缺点。

综合以上分析，笔者提出一种采用多尺度卷积神经网络的故障辨识方法。首先，设计多尺度卷积提取频域数据中的多粒度信息；其次，采用IN 对多尺度特征进行归一化并在深度方向进行特征拼接；然后，构造注意力机制对拼接后的特征图进行自适应加权，减小信息冗余，再进一步使用卷积提取深层抽象特征；最后，利用全连接层对特征进行信息整合与分类，完成智能故障辨识任务。通过实验数据将本研究方法与其他智能故障辨识方法进行对比与分析，验证其有效性与泛化性。

1 基本概念简介

1.1 实例归一化

文献［13］在图片风格迁移任务中提出IN，将特征图的对比度进行归一化以减少特征图之间的风格差异性，解决了BN 应用过程中的不足。IN 的数学形式可以描述为

其中：Xl(c)为第l层通道c 的输入特征图；为标准化后的特征图；zl(c)为通道c 的输出；μc为通道c 输入特征图数据的均值；σc为通道c 输入特征图数据的标准差；ε为防止分母出现零值的小常数；γl(c)与βl(c)分别为标准化后特征图中通道c 的缩放因子与平移因子。

式（1）中均值与标准差可以计算为

其中：W为通道c 特征的宽度。

1.2 注意力机制

注意力机制能够模拟人类视觉注意力机制，对包含敏感特征信息部分投入更多关注度，从大量特征信息中筛选出对当前任务有用的关键信息，以提高网络的识别能力［14］。

2 多尺度卷积神经网络模型的构造

笔者提出一种多尺度卷积神经网络结构，如图1 所示，包括多尺度卷积模块、注意力加权模块、深层卷积模块与全连接模块。

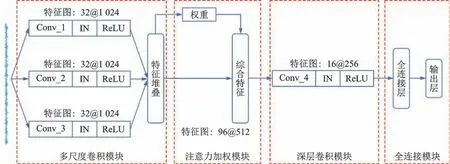
图1 多尺度卷积神经网络结构Fig.1 Structure of NMS-CNN

2.1 多尺度卷积模块

图1 中的多尺度卷积模块，使用3 个卷积层提取输入数据的特征，然后将其拼接。其中，3 个卷积层的卷积核尺寸参数互不相等，以此实现多尺度特征提取。因为小样本与噪声干扰的情况下训练样本与测试样本特征之间存在分布差异，因此在每个卷积层中引入IN 减小这种分布差异，以提高模型的泛化性。

卷积操作的数学形式可以表示为

其中：I0与I1分别为输入与输出特征图；Kl与bl分别为第l个卷积核的权重与偏置；*表示卷积运算；p为卷积区域。

对得到的特征进行降采样以降低特征图的维数与网络参数，加快计算速度并且防止网络过拟合，其数学形式为

其中：A为池化操作后输出的特征图；P(.)表示池化操作；r为池化区域；X为输入特征图。

按照式（1）对特征图进行归一化操作，减小训练样本与测试样本特征的分布差异，增加网络的泛化能力，再将归一化后的特征图进行非线性映射以增强特征的表示能力与可分性。选择整流线性单元（rectified linear unit，简称ReLU）作为激活函数，其数学形式为

将3 种不同尺度卷积提取到的特征图，分别表示为X1，X2与X3，并且在深度方向使用张量拼接方法将其堆叠，实现特征融合。经过拼接后的特征图可以表示为

其中：concat 表示张量的拼接操作。

2.2 注意力加权模块

由于多尺度卷积模块直接将不同尺度卷积层学习的特征进行堆叠，因此存在信息冗余，需要对拼接完成的特征图使用注意力机制对其自适应加权，使模型更加关注对当前分类任务有用的信息。

注意力机制结构如图2 所示，主要包含挤压、激励及重标定［15］等3 个步骤。

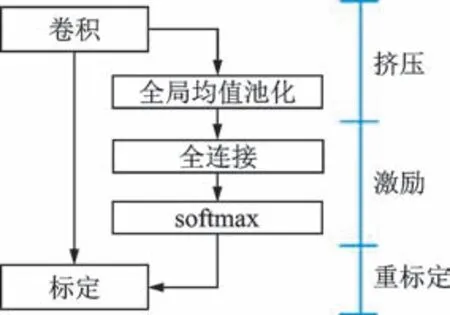
图2 注意力机制结构Fig.2 Structure of attention mechanism

1）特征压缩：通过全局均值池化将全局特征压缩进一维向量中获取每个通道的统计信息，即

其中：zc为通道c 压缩后的统计值；Xc为通道c 的特征图；L与T分别为特征图的长度与高度。

2）特征激励：经过挤压操作后得到具有c个元素的一维向量表示特征图中每个通道的统计信息，然后连接2 个全连接层学习通道的权重参数。2 个全连接层神经元的数目均设置为特征图通道数，第2 个全连接层使用softmax 激活函数生成不同通道的权重，其数学表达式为

其中：δ为ReLU 激活函数；W1与W2分别为2 个全连接层的权重；σ(.)为softmax 激活函数。

3）特征重标定：把特征激励操作后softmax 输出的一维向量作为通道的权重，然后将通道权重与原特征图逐通道相乘完成特征重标定。整个过程数学形式为

2.3 深层卷积模块

通过注意力加权后继续使用一个卷积模块来进一步提取深层抽象特征信息，该卷积模块包括卷积层、池化层、IN 以及激活函数。

2.4 全连接模块

全连接模块主要对前1 层输出的特征图进行信息整合与分类。包含1 个全连接层与1 个输出层。其中，全连接层使用ReLU 激活函数，而输出层使用softmax 激活函数。softmax 函数的公式为

其中：pj为网络输出属于第j类的概率；zj为第j个输出神经元的逻辑值；k为输出神经元的数量。

2.5 模型训练

本研究使用softmax 分类器输出的概率分布与真实的概率分布之间的交叉熵作为损失函数，用于衡量模型预测类别与真实类别分布之间的差异，其公式为

在误差反向传播阶段使用Adam 算法［16］优化并更新模型参数，使模型参数取得最优解。模型训练过程中将算法的学习率设为0.001，网络最大训练轮数设为20，当累计3 轮训练误差未下降时将学习率调整为原来的50%。

3 设计的NMS-CNN 故障辨识方法

笔者提出一种采用NMS-CNN 的智能故障辨识方法，其故障诊断流程见图3，具体步骤如下。

1）预处理：①通过安装在轴承座上的加速度传感器采集轴承的振动信号；②使用数据增强技术［6］对振动信号进行重叠采样；③对采样完成的数据进行FFT，构造数据集并将其划分为训练集与测试集。

2）模型训练：①构建网络，对网络权重进行初始化；②使用训练数据集对网络进行训练，输出网络模型。

3）模型测试：将测试数据集输入已经训练好的网络中进行测试。

4 算法验证结果与分析

采用美国凯斯西储大学轴承数据中心（CWRU）公开数据［17］验证第3 节方法的有效性。

4.1 CWRU 数据集验证

4.1.1 数据集描述

轴承实验台如图4 所示，由1.5 kW 的三相感应电动机、测力器、扭矩传感器及电子控制器等组成。使用电火花加工方式分别在轴承的内圈、外圈及滚动体引入单点缺陷，故障尺寸分别为0.177 8，0.355 6及0.533 4 mm。2 个加速度传感器通过磁力吸座安装在电机的驱动端和风扇端采集轴承在不同状态下的振动信号，采样频率为12 kHz。

图4 轴承实验台Fig.4 The test rig in the CWRU

笔者使用0.745 7 kW 负载下轴承风扇端的振动信号，采用重叠采样方法构造轴承故障数据集。采样长度设置为2 048，数据集中共包含9 种故障状态以及1 种正常状态的样本。凯斯西储大学轴承故障数据集如表1 所示。

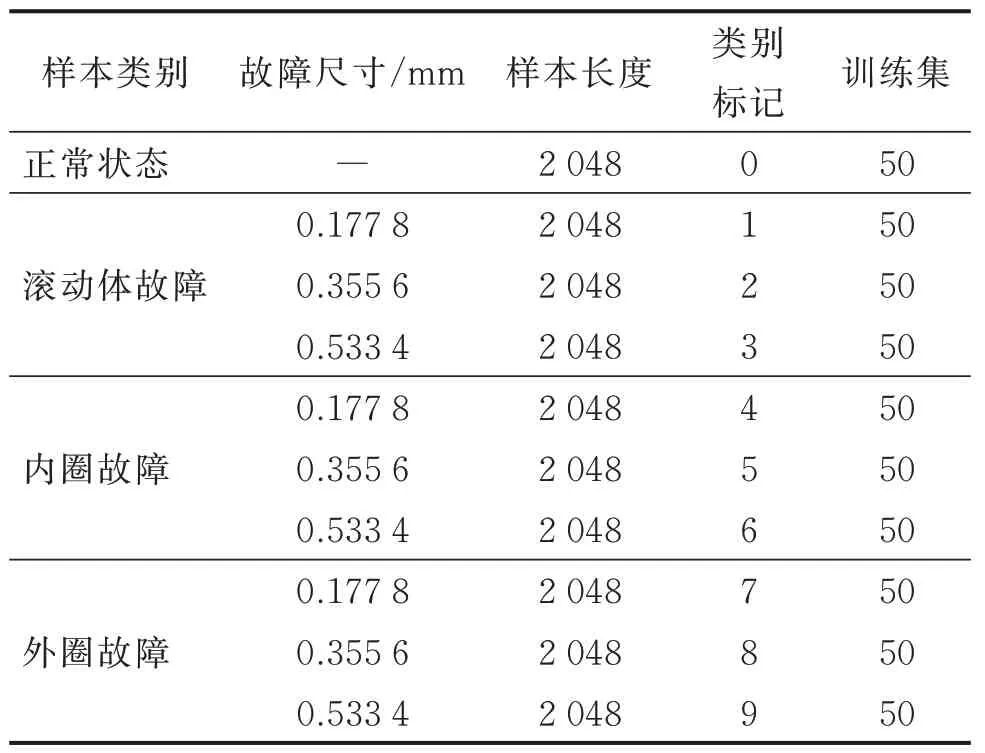
表1 凯斯西储大学轴承故障数据集Tab.1 The dataset of fault bearing sample from CWRU

4.1.2 网络参数设置

通过多次实验得到NMS-CNN 的主要结构参数如表2 所示。其中：CN 为卷积核数量；kernels 为卷积核尺寸；p为池化区域宽度，units 与activation 分别为密集连接层中神经元的数量与激活函数；rate为Dropout 层的比率。

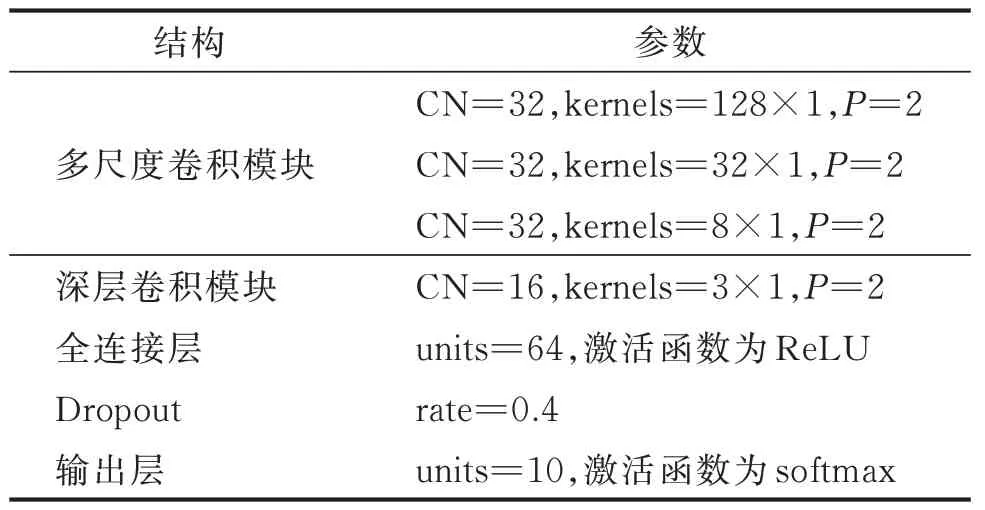
表2 NMS-CNN 主要结构参数Tab.2 Main structural parameters of NMS-CNN

4.1.3 不同样本数量下的性能分析

机械在运行期间长期处于正常状态，故障样本难以获取。为了验证不同的训练样本数量对本研究方法识别准确率的影响，分别设置训练集中每类样本的数量为10，20，30，50，100 以及200，测试集中每类样本的数量为100。由于神经网络的权值以及偏置是随机生成的，因此每个实验重复进行20 次以验证模型的稳定性。不同训练样本数量对于识别准确率的影响如表3 所示。

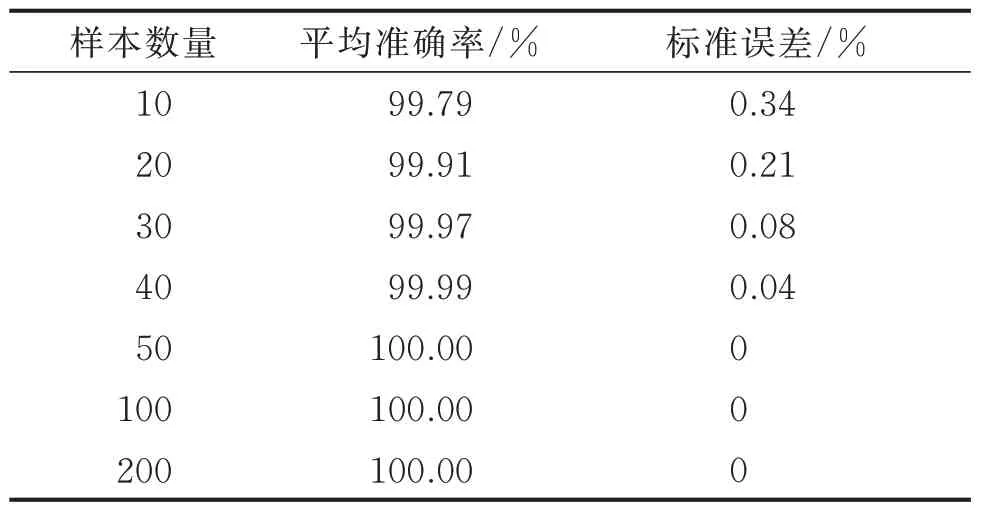
表3 不同训练样本数量对于识别准确率的影响Tab.3 Diagnosis result using different number of training samples

由表3 可以看出：当训练集中每个类别样本的数量只有10 个时，本研究方法就已经达到99.79%的分类准确率，说明其能够在较小的训练样本下完成故障辨识任务；随着训练样本数量的增加，所提方法的识别准确率与稳定性也逐渐上升；当训练集中每个类别样本的数量超过50 个时，20 次实验均能实现100%的识别准确率。根据以上实验结果，本研究实验训练集中每类样本的数量均设为50，测试集中每类样本的数量设为100。

4.1.4 模型在噪声环境下的性能分析

由于工业现场环境复杂，采集到的信号受噪声干扰严重，因此模型能否在噪声环境下达到较高的识别准确率成为其在工业应用中的一个关键问题。评价信号中噪声强弱的标准是信噪比，其定义为

其中：Psignal与Pnoise分别为信号与噪声的功率。

为了讨论本研究方法的抗噪性，使用原始信号进行训练，然后对其注入高斯白噪声进行测试。将本研究方法与目前主流的支持向量机（support vector machine，简称SVM）、K-近邻算法（k-nearest neighbors algorithm，简称KNN）、多层感知机（multilayer perceptron，简称MLP）、基于快速傅里叶变换的深度神经网络（fast Fourier transformation-deep neural networks，简称FFT-DNN）［4］及WDCNN［6］等进行对比实验分析。其中，FFT-DNN 包含3 个隐含层，每层神经元的数量为500，200 及100。传统故障辨识方法通常需要对振动信号手动提取特征值，再将其输入到算法中完成故障分类。首先，使用文献［2］的方法提取特征值并进行归一化预处理；其次，分别输入SVM，KNN 以及MLP 中进行故障辨识。其中：SVM 的核函数为径向基核函数，惩罚因子c=10；KNN 算法的邻近点数K设置为5；MLP隐含层包含50 个神经元，激活函数为ReLU。每个实验均重复进行20 次，不同噪声下的对比结果如图5 所示。

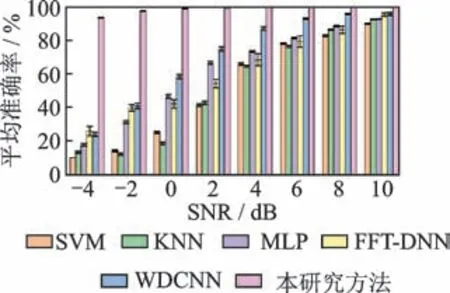
图5 不同噪声下的对比结果Fig.5 The comparison result under different noisy environment

由图5 可以看出，SVM，KNN 及MLP 等基于机器学习的故障辨识方法在数据受到噪声干扰的情况下识别准确率快速下降，说明由于自身浅层算法的限制，很难在测试数据受到噪声干扰的情况下取得较高的识别准确率。当信噪比为10 dB 时，FFT-DNN 与WCDNN 的识别准确率分别为95.58% 与95.89%，但是仍然低于本研究方法的99.97%。随着信噪比逐渐下降，FFT-DNN 与WDCNN 的识别准确率也开始下降，结合文献［6］中的实验结果，说明训练数据过少而出现了过拟合现象；相比之下本研究方法在信噪比为-4 dB 时仍然能够取得93.73%的识别准确率，没有出现过拟合现象，证明本方法具有较强的鲁棒性，在强噪声干扰下仍然能够准确实现故障分类。

4.1.5 IN 的有效性验证

为了验证卷积神经网络中IN 的抗噪效果，以笔者提出的NMS-CNN 作为主干网络，对于使用IN（本研究方法）、使用BN 以及不使用任何归一化方法3 种情况进行对比实验。结果如图6 所示。

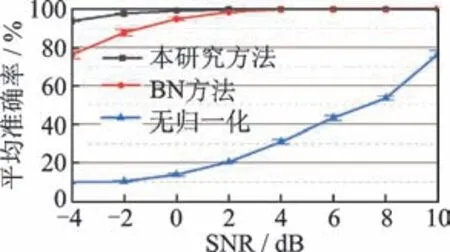
图6 3 种归一化方法的结果对比Fig.6 The comparison result of three methods

由图6 可以看出：如果不使用归一化方法，模型很难取得较高的识别准确率，当信噪比为10 dB 时其测试准确率只有76.55%，随着信噪比逐渐下降，模型的识别准确率也在迅速下降，最终在信噪比为-4 dB 时准确率降至10%；当使用BN 作为归一化方法之后，模型的识别准确率与稳定性得到极大提升，但仍低于本研究方法；当信噪比大于4 dB 时，IN与BN 均能够达到99%以上的识别准确率；随着信噪比逐渐下降，模型的测试准确率与稳定性均开始下降，在信噪比达到-4 dB 时，IN 相比于BN 测试准确率提升了23%，标准误差下降了83%。以上结果说明IN 能够提升模型的抗噪性与稳定性。

4.1.6 变负载情况下的性能分析

机械的负载发生变化时转速也会随之变化，测得的信号也有所不同。该数据集中共包含3 种不同的负载，分别为0.745 7，1.491 4 及2.237 1 kW，将其记作L1，L2及L3。分别使用L1，L2及L3下的信号作为训练数据，然后使用其他2 个负载下的振动信号作为测试数据。例如使用L1下的数据进行训练，再使用L2下的数据进行测试，将实验结果表示为L1->L2。每个实验重复进行20 次，不同方法在变负载下的实验结果如图7 所示。

图7 不同方法在变负载下的实验结果Fig.7 The comparison result under 6 domain shifts

SVM，KNN，MLP，FFT-DNN，WDCNN 与本研究方法在6 种变负载情况下测试的平均准确率分别为93%，92.78%，92.24%，73.3%，89.97% 与97.13%。可以发现，本研究方法在负载发生变化时能够取得最好的效果。由图7 可知，FFT-DNN 准确率下降至75%左右，说明其适用性受到了限制。本研究方法在L3->L1的情况下准确率相比SVM，KNN 及MLP 等方法优势不突出。为了进一步分析其原因，将4 种方法在L3->L1下的识别结果绘制为混淆矩阵，如图8 所示。

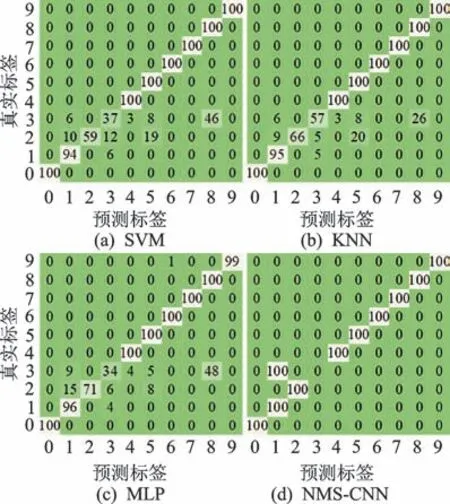
图8 4 种方法在L3->L1下的识别结果Fig.8 Identification results of 4 methods at L3->L1

由图8 可知：本研究方法将第3 类样本全部错分为第1 类，不能很好地区分0.177 8 与0.533 4 mm 内圈故障样本，导致识别结果相对其他方法优势不明显；本研究方法中其他类别的样本全部分类正确，相对于其他方法具有一定的优势。

结合4.1.4 节中的实验结果发现：SVM，KNN，MLP 及WDCNN 等方法抗噪性差，但是变负载效果较好，因而难以适应机械复杂的工作环境；而本研究方法在小样本的情况下兼具良好的抗噪性与变负载性能，表明NMS-CNN 能够从频域数据中学习到鲁棒性更好的特征。

4.1.7 特征可视化分析

为了从直观上了解网络的注意力机制对数据变换的效果，以滚动体-0.355 6 mm 故障样本作为神经网络的输入，将数据通过注意力加权模块前后的神经元激活进行可视化表达［6］，结果如图9 所示。其中：水平方向表示特征的通道，垂直方向表示特征的长度。

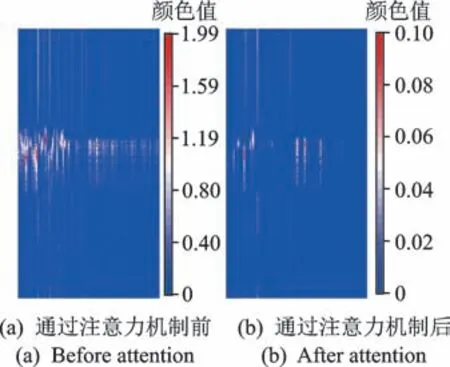
图9 滚动体-0.355 6 mm 数据通过注意力加权模块神经元激活可视化Fig.9 Visualization of the activation from attention module for ball-0.355 6 mm

图9 中不同颜色表示神经元被激活的程度：蓝色表示神经元没有被激活；红色表示神经元被最大激活。由图可知：通过注意力机制前大多数通道的神经元都存在激活状态，参与最终的分类计算；通过注意力机制进行加权后，大多数的通道都变为蓝色，仅有少数几个通道的神经元存在最大激活，表明注意力机制能够抑制冗余信息，更加关注对分类任务有用的特征通道。

4.2 本实验室轴承数据验证

4.2.1 本实验室数据集描述

为了进一步检验NMS-CNN 在其他数据上的效果，使用本实验室轴承数据构造数据集。转子实验台如图10 所示。

图10 转子实验台Fig.10 Experiment of rotor vibration

该实验台运行转速为2 600 r/min，共模拟正常、滚动体故障、保持架故障、内圈故障以及外圈故障5 种运行状态。使用加速度传感器采集轴承座的振动信号，采样频率设为20 kHz。实验室轴承故障数据集如表4 所示。

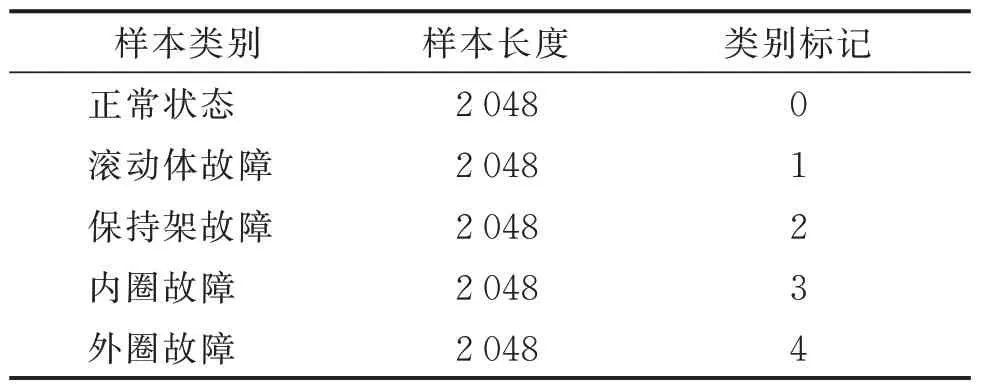
表4 实验室轴承故障数据集Tab.4 The dataset of fault bearing sample from laboratory data

4.2.2 本数据集不同样本数量下的性能分析

同样设置训练集中每类样本的数量为10，20，30，50，100 及200，测试本研究方法使用不同数量的训练样本取得的效果，测试集中每类样本的数量为100。每个实验重复进行20 次，实验室数据不同训练样本数量对于识别准确率的影响如表5 所示。

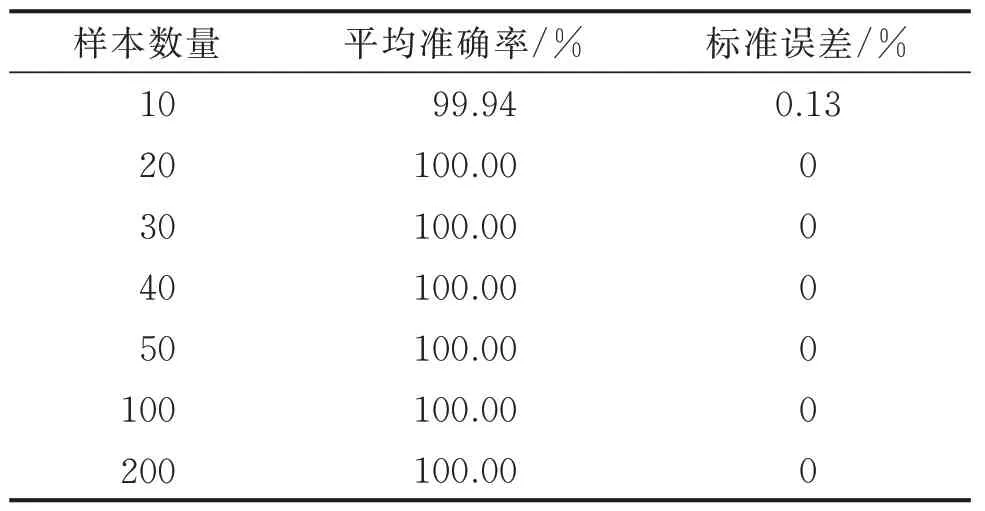
表5 实验室数据不同训练样本数量对于识别准确率的影响Tab.5 Diagnosis result using different number of training samples from laboratory data

由表5 可知：使用实验室数据集，每类训练样本仅有10 个时，NMS-CNN 已经能够取得99.94%的平均准确率；每类训练样本数量超过20 个时，所有实验全部识别准确，说明本研究方法在小样本的情况下能够准确地完成故障辨识。

4.2.3 本数据集模型在噪声环境下的性能分析

在测试数据中加入不同信噪比的高斯白噪声，验证模型在受不同强度噪声影响下识别准确率的变化情况，对比结果如图11 所示。

图11 不同噪声下的对比结果Fig.11 The comparison result under different noisy environment

由图11 可知，当测试样本受噪声污染严重时，传统的机器学习方法在本实验室数据集上取得的平均准确率在40%左右，可以认为该模型不具有通用性；随着信噪比上升，FFT-DNN 与WDCNN 的平均准确率逐渐上升；NMS-CNN 在-4dB 噪声下仍然能够取得98.16%的平均准确率。实验结果表明，本研究方法在不需要额外降噪算法的情况下仍具有较好的抗噪性能。

5 结束语

针对基于深度学习的故障辨识方法效果受制于训练样本数量与质量这一问题，提出一种采用多尺度卷积神经网络故障辨识方法，在训练样本数量较小时能够从频域数据中学习到鲁棒性的特征，实现了对滚动轴承健康状态的有效识别。实验结果表明，本研究方法能够在小样本的情况下完成故障辨识任务，并且其泛化性与稳定性高于其他智能故障辨识算法。