漏表面波IMF1能量识别无砟轨道脱空适用性研究∗

马嘉霈，袁笙哲，3，肖军华，李 航，潘 越，苏志鹏

（1.同济大学道路与交通工程教育部重点实验室 上海，201804）（2.上海市轨道交通结构耐久与系统安全重点实验室 上海，201804） （3.广西交通设计集团有限公司 南宁，530029）

引言

板式无砟轨道CA 砂浆层脱空是高铁线下结构病害的主要形式之一。由施工不当及长期运营所导致的CA 砂浆层脱空会劣化轨道的动态平顺性，影响行车的舒适性和安全性。为了能够及时采取维护措施以降低安全风险，对脱空病害准确高效的检测是重要前提［1-3］。

弹性波是外力作用或扰动引起的应力和应变在弹性介质中传递的形式，由于其传播速度与介质自身物理力学参数密切相关，被广泛应用于检测结构内部状态。弹性波法主要包括冲击回波法和表面波法，因其精度高、操作方法简单及抗干扰能力强等优点而适合于高铁无砟轨道层间脱空检测［4-5］。例如：全波场弹性波法通过波传播现象识别轨下结构缺陷［6］；通过布置多阵列加速度器获取轨道板面上波动场分布［7］；通过对比频域内共振频率峰值等参数定位砂浆层内部缺陷等［8］。为提高冲击弹性波法的检测效率，近年来发展出采用麦克风代替接触式传感器的空耦检测技术。Zhu 等［9］提出空耦冲击回波法并运用于混凝土板损伤检测，利用麦克风采集冲击点近场的共振模态波信号，依据其峰值频率判断混凝土内部损伤情况，实验表明，共振模态波信号相较于加速度信号具有更高的信噪比，同时完整保留了信号的频域特征，可满足混凝土板损伤检测的分析要求。Oh 等［10-11］基于空耦冲击回波法研究了不同形状的浅层分层损伤的共振频谱特性和不同敲击位置对信号频谱图的影响，并提出多维度的麦克风阵列冲击共振法体系。由于共振模态波主要分布在冲击点附近，对测点布置密度要求较高，限制了空耦冲击回波法的平面检测范围［12-13］。空耦表面波法是利用混凝土层状结构受到冲击激励后所产生的漏表面波信号具有Lamb 导波特性的原理进行层间脱空识别。由于面波能量占冲击弹性波的比重大，传播过程中能量衰减慢，因此检测范围较广，但由于缺乏对脱空特征指标的研究，目前难以将该方法用于板式无砟轨道脱空检测［14-15］。

针对上述问题，笔者探讨了基于漏表面波IMF能量的高铁线下结构脱空检测方法。依据弹性波传播理论建立高铁板式无砟轨道声固耦合有限元模型，模拟冲击弹性波在轨下结构及空气中传播过程，分析轨道板上方空气层漏表面波传播特性，并以由希尔伯特黄变换得到的漏表面波第1 阶本征模函数IMF1能量作为脱空特征指标，最终建立该指标对脱空参数的响应规律。

1 板式无砟轨道中漏表面波传播特性

在混凝土结构表面施加竖向冲击荷载后，会生成在结构中传播的纵波、横波以及沿结构和空气交界面传播的瑞利波。瑞利面波的传播实质是通过气固交界处的介质微粒振动实现，而介质微粒振动又带动了空气粒子的运动，形成了以一定角度传播的声波，表现为表面波泄漏至空气中的能量，故称该声波为漏表面波。当混凝土结构的厚度较小时，纵波与横波在结构上下表面发生波形转换，经反射耦合后以Lamb 波的形式传播［16-17］。在冲击点下方，由于纵波在结构上下表面来回反射，引起小范围的周期性振动并在空气中形成柱状的共振模态波［18］。

文献［19-20］研究了利用麦克风采集漏表面波的可行性，试验表明，厚墙和薄板的漏表面波分别具有瑞利波和Lamb 波的特性。根据弹性波传播理论，弹性波向下传播过程中，遇到不连续界面时会发生明显的能量反射现象，反射系数的大小与脱空厚度无关，取决于反射界面处上下层材料的弹性模量。Lamb 波在波导内的传播过程中遇到层间脱粘时向下泄露能量减少，反射能量增多，对介质缺陷反应敏感，常用于铝材和复合材料等薄板结构损伤检测［21-22］。Lamb 波具有频散和多模态的特点，各模态不同频率成分对脱空损伤的敏感性有所差异，因此在复合材料损伤检测中往往需要进行激励参数优化［23-24］。高铁板式无砟轨道为典型的层状结构，受到冲击荷载作用后能产生分布明显的共振模态波与漏表面波，且漏表面波具有Lamb 波的传播特性，故笔者依据Lamb 波层间损伤检测原理，研究漏表面波能量对高铁线下结构层间脱空的响应规律，分析不同频率成分的脱空敏感性，为脱空特征指标的建立提供依据。

1.1 室内实尺模型试验

室内实尺模型试验如图1 所示，按照相关规范浇筑板式无砟轨道实尺模型，在模型板中预设一个0.4 m×0.4 m 的自密实混凝土层脱空缺陷，脱空深度贯通该层。试验设备包括模态力锤、MPA201 传声器、4 通道DH5922D 动态信号测试分析仪、计算机及BNC 连接线。设备连接调试完毕后，在单次模态力锤冲击激励下，通过信号分析仪采集力锤的力信号及传声器的声压信号，并储存至计算机中进行后续比较分析。测点布设如图2 所示，冲击点和测点纵向布设在板中位置，减小边界反射的影响，偏移距为0.2 m，道间距为0.05 m，冲击点至脱空中心的水平距离为0.1 m，传声器探头距离轨道板表面高度为0.05 m。

图1 室内实尺模型试验Fig.1 Indoor full-scale model test

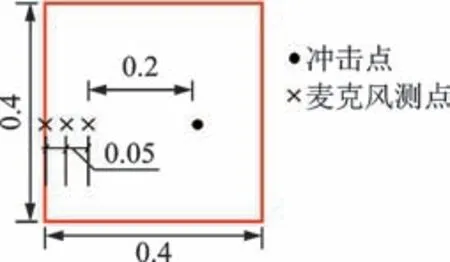
图2 测点布设示意图（单位：m）Fig.2 Layout diagram of survey points(unit:m)

设置采样频率为50 kHz，得到冲击荷载激励下3个不同测点的实测声压数据，如图3 所示。漏表面波传播速度快，能量衰减慢，而直达声波速度较慢，能量衰减明显。室内试验中3 个测点先后采集得到漏表面波波谷对应时刻分别为4.620 82，4.620 84 和4.620 86 s，估算得到漏表面波速度约为2 500 m/s。

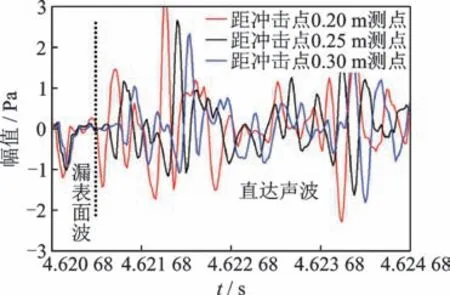
图3 各测点实测声压数据Fig.3 Measured sound pressure data of each measuring point

1.2 数值模型计算与试验结果对比

依据实尺模型，采用COMSOL Multiphysics 建立CRTSⅢ型板式无砟轨道-空气耦合模型。由于板式无砟轨道结构的厚度远小于其纵向长度和横向宽度，冲击弹性波在结构中的传播可近似为平面应变问题［25］。实尺试验中的脱空形状为正方形，且测点沿正方形中心线布设，含脱空有限元模型如图4所示，根据模型的对称性，为提高计算效率，考虑将有限元模型简化为二维模型。

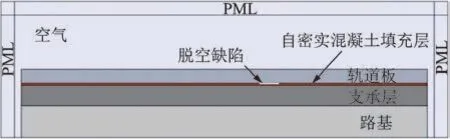
图4 含脱空有限元模型Fig.4 Finite element model with defect

板式无砟轨道结构长为6 m，由上至下依次为轨道板、自密实混凝土填充层、支承层以及路基，上部及两侧为空气域，最外侧为完美匹配层（perfectly matched layer，简称PML），用于消除弹性波在模型边界的反射。对于脱空缺陷，采用材料换填法进行模拟。模型采用自由三角形网格，最大单元取0.01 m。各部分材料参数见表1。由于麦克风采集到的有效冲击弹性波波长通常大于100 mm，传播至钢筋断面时以绕射为主，因此轨道结构中钢筋对冲击弹性波传播影响较小，故模型中未设置钢筋。

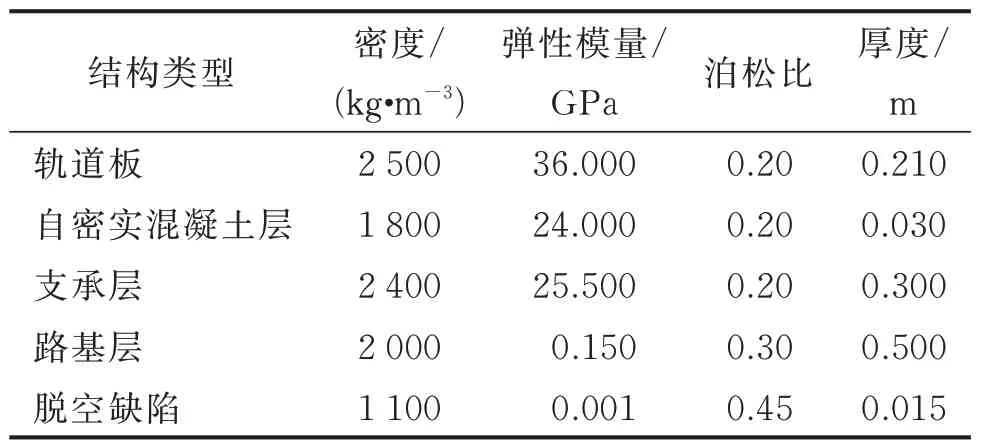
表1 材料参数Tab.1 Material parameters

数值模型中轨道板的表面波速度为2 225 m/s，略小于理论计算得到的表面波速度2 233 m/s 和试验估算的表面波速度2 500 m/s。考虑试验测点道间距和采样频率均相对较小，误差处于可接受范围。直达声波可视为环境噪声，由于表面波理论速度远大于空气中的声波速度，故通过选用Hanning窗可滤除信号中的噪声部分，提高信号的信噪比。

进一步将采集得到的冲击力离散信号作为插值函数施加至轨道板上表面，脱空尺寸、各测点位置与室内试验一一对应，计算得到相应位置的声压信号。以距离冲击点0.25 m 测点为例，对比实测信号与模拟信号中的漏表面波成分及其频谱，其时域曲线和频域曲线分别如图5，6 所示。在时域上，模拟漏表面波信号的负幅值小于实测信号，而正幅值大于实测信号；在频域上，模拟信号的频率峰值略大于实测信号，但低频幅值普遍低于实测信号，其原因为实际条件下弹性波的低频成分在轨道板中的绕射作用更强，反射至轨道板上表面并泄漏至空气中的能量更大，同时环境及检测设备噪声的影响也会导致低频成分增大。数值模拟结果在时、频域上与实测数据趋势相近，故依据数值分析方法开展漏表面波信号与轨道板脱空相关性研究是可行的。

图5 实测信号与模拟信号时域曲线Fig.5 Curve of measured signal and analog signal in time domain

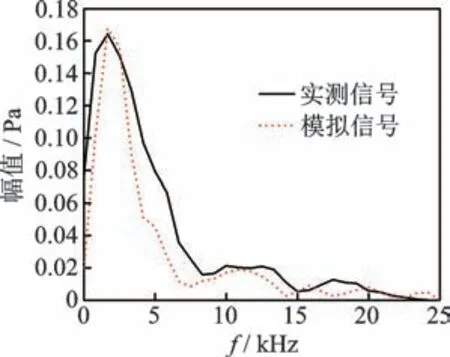
图6 实测信号与模拟信号频域曲线Fig.6 Curve of measured signal and analog signal in frequency domain

1.3 不同板式无砟轨道结构中漏表面波传播特性模拟对比

分别建立CRTSI，CRTSII 和CRTSⅢ型3 种板式无砟轨道结构模型，填充层材料参数差异如表2所示，分析冲击弹性波在不同板式无砟轨道结构中的传播特性。图7 所示为不同无砟轨道模型在冲击点右侧0.4 m 出现脱空长度为0.4 m 的CA 砂浆层脱空时，6 ms 时刻的波场分布。

表2 填充层材料参数差异Tab.2 Material parameters difference of filling layer

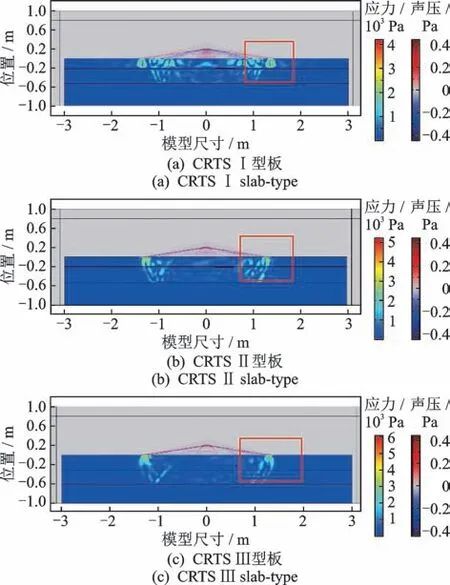
图7 冲击点右侧0.4 m CA 砂浆层脱空长度为0.4 m波场分布Fig.7 Wave field distribution when the void length of the CA mortar layer at 0.4 m on the right side of the impact point is 0.4 m

由图7 可知：CRTSI 型板中相邻结构层间反射作用较大，因此CA 砂浆层脱空对波场分布影响小；CRTSIII 型板由于自密实混凝土层模量远大于CA砂浆层模量，填充层与上下结构层的刚度比减小，应力波传播至自密实混凝土层时以折射为主，边界反射作用减小，尽管应力波在CRTSII 型板与CRTSIII 型板中能量分布特征及声场分布规律相似，但应力波在III 型板中传播时能量更集中在轨道板上表面，对轨道板脱空的检测能力较差；在CRTSII 型无砟轨道板中，漏表面波在空气域中的分布较为集中，导波特性明显，故利用漏表面波对该结构进行脱空特征的分析效果较好。

2 脱空特征的判定方法

2.1 脱空工况设置

为直观反映无砟轨道板脱空对漏表面波频散特性的影响，研究漏表面波各频率成分对脱空的检测敏感性，进一步确定脱空特征指标，以CRTSII 型无砟轨道板为对象，在数值模型中建立多种脱空工况，并提取不同脱空工况下的漏表面波频散曲线进行比较。

依据脱空长度及脱空中心至冲击点距离的不同，建立26 种计算工况，脱空长度考虑0.1，0.2，0.3，0.4 和0.5 m 这5 种情况，脱空中心至冲击点距离分别为0（正下方），0.1，0.2，0.3 和0.4 m。信号采集方面，在荷载冲击点上方0.05 m 处，沿水平向右方向每间隔0.1 m 共布置11 个测点探针，脱空工况及探针设置如图8 所示，声压检测范围为距离冲击点1 m以内，采样频率取50 kHz。冲击荷载设置方面，数值模拟中力锤对混凝土试件表面的瞬时冲击作用力可简化为作用时间内关于幅值的正弦函数。本研究在轨道板上表面正中心设置垂向冲击点荷载，计算公式为

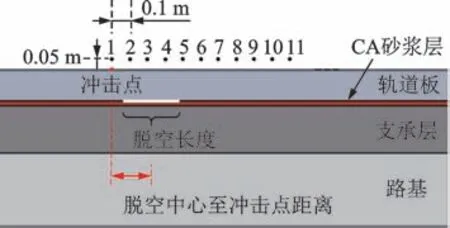
图8 脱空工况及探针设置示意图Fig.8 Schematic diagram of void condition and probe setting

其中：Fmax为冲击荷载幅值，取1 kN；T为冲击荷载持续时间；t为函数时间变量。

T决定所产生应力脉冲的频率成分。通常在混凝土结构冲击响应试验中，冲击弹性波的最大有效频率上限取1.25/T，为保证有效频率范围内的弹性波信号能量充足，模型中T取8×10-5s。

2.2 脱空特征判定方法

分析漏表面波的频散特性需要明确其频散曲线，笔者采用相移法进行频散曲线提取。对于时间-空间域的多道麦克风信号d（x，t），对时间轴作傅里叶变换，得

由傅里叶变换的性质可知，变换后信号U（x，f）可以表示为幅值谱和相位谱的乘积形式

其中：ph(x，f)为相位谱，包含了关于频散的所有信息；A(x，f)为幅值谱，包含了振幅衰减、球面扩散等信息。

由于相位分量ph(x，f)可以表示为e-iφx，式（3）可写为

其中：ϕ=2πf/Vf，Vf是当频率为f时对应的相速度。

在空间坐标方向作积分可得

式（5）是对幅值谱归一化后的积分。若某个频率值所对应特定的相位处出现极大值，说明该相速度值为频散曲线中所求的相速度。本研究对结构无脱空、冲击点正下方脱空长度为0.4 m、冲击点右侧0.4 m 处脱空长度为0.4 m 这3 种脱空工况进行分析，分别选取探针4～11（距冲击点水平距离为0.3～1 m）1 ms 内的声压信号，得到各工况漏表面波频散曲线如图9 所示。

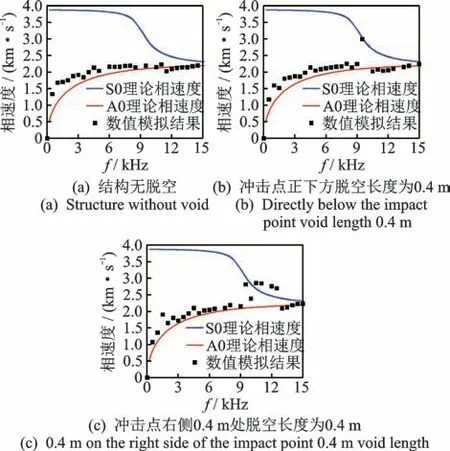
图9 不同脱空工况下的漏表面波频散曲线Fig.9 Dispersion curves of leaky surface waves under different void conditions

图9 中，黑点代表采用相移法得到的漏表面波频散点，红线与蓝线分别为轨道板中Lamb 波的基阶反对称模式和对称模式理论计算频散曲线。由图可知：当无砟轨道板无脱空时，漏表面波主要表现出Lamb 波基阶反对称模式频散特性；当无砟轨道板出现脱空时，漏表面波中9 kHz～12 kHz 频段成分易发生模式变换，表现出基阶对称模式频散特性。模式变换现象可通过分析Lamb 波A0 模式在不同频率下的波结构进行解释。不同频率下0.2 m 厚轨道板中Lamb 波A0 反对称模式波结构如图10 所示。由图可知：随着频率的增大，A0 模式在轨道板表面的离面位移（红线）随之增大，即冲击弹性波传播过程中引起的轨道板上下表面振动位移增大；当轨道板无脱空时，受边界约束作用，冲击弹性波以A0 模式为主，能量主要泄漏至下部支承层；当轨道板出现脱空时，可将脱空区域内轨道板近似为自由板，冲击弹性波的高频成分在脱空处反射更为明显，故表现出了S0 模式频散特性。由此可见，漏表面波中高频成分包含无砟轨道板脱空特征，提取该频段成分进行分析更有利于脱空识别。

图10 不同频率下0.2 m 厚轨道板中Lamb 波A0 反对称模式波结构Fig.10 A0 antisymmetric mode wave structure of Lamb wave in 0.2 m thick track plate at different frequencies

3 脱空特征的提取方法

3.1 希尔伯特-黄变换

由于漏表面波具有频散性，传播过程中信号成分变化复杂，属于非平稳随机信号，需利用有效信号处理技术提取高频脱空特征信号。希尔伯特-黄变换通过经验模态分解（empirical mode decomposition，简称EMD），将各种频率成分以本征模函数的形式从时间序列中分离，再运用希尔伯特变换对各IMF 分量进行谱分析。相较于傅里叶分解和小波分解，EMD 分解的基函数是自适应的，因此更有利于非平稳数据处理，故本研究选用希尔伯特-黄变换处理声压信号。对信号X(t)的EMD 分解过程如下。

1）找出X(t)的所有极大和极小值点，运用3 次样条差值函数分别拟合时间序列的上下包络线。定义m0为上下包络线的均值包络线，将原时间序列X(t)减去均值包络线，即可得到去掉低频项的新时间序列h0，即

一般情况下h0不是一个平稳时间序列，故需重复上述过程。如果h0的平均包络线为m1，则去掉低频包络线后的新时间序列h1为

重复上述过程，经过n次循环后，当得到的平均包络mn趋于0 时，定义此时hn为第1 阶IMF 分量，用c1表示，其代表信号中的最高频率成分。

2）得到第1 阶IMF 分量后用原信号X(t)减去c1，便得到去掉高频成分的新序列y1，重复步骤1，可得到第2 阶IMF 分量c2。反复重复步骤1 和2，便可得到更多阶次的IMF 分量，直到剩余的成分yn不能再分解为止，此时yn代表时间序列X(t)的残余项或者趋势项。整个分解过程可以表示为

对各IMF 分量进行希尔伯特变换，得到信号的瞬时频率为

其中：Re 表示取实部，得到的H(ω，t)即希尔伯特时频谱，表示瞬时振幅在频率-时间平面上的分布。

希尔伯特边际能量谱定义为

其中：L为信号的长度。

h(ω)能精确描述信号能量随瞬时频率的分布情况，通过对能量谱进行频域积分，得到信号能量

3.2 脱空特征信号提取

图9 中，探针6 采集的信号主要是漏表面波，故以探针6 为例，采集0～1 ms 内声压数据进行EMD分解得到各阶IMF，并对各IMF 信号进行频谱变换，如图11 所示。漏表面波的高频脱空特征信号主要分布在IMF1分量上，而IMF2和IMF3中几乎不含高频成分，故笔者仅对IMF1进行希尔伯特变换得到其边际能量谱，对边际谱做频域积分得到IMF1能量，以便为基于IMF1能量构建脱空特征指标提供依据［26］。

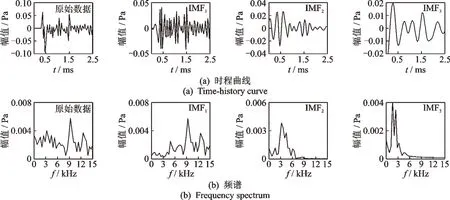
图11 探针6 信号EMD 分解及各阶IMF 频谱Fig.11 EMD decomposition of probe 6 signal and IMF spectrum of each order

4 IMF1 能量分布与无砟轨道脱空特征的关系

同时处理11 个探针数据，提取信号1 ms 内IMF1能量，建立探针相对冲击点距离与各探针信号能量的联系，得到声压能量的空间变化情况。图12 为IMF1能量随传播距离变化曲线，靠近冲击点处IMF1能量较大，这是因为信号中包含了共振模态波，根据混凝土板中的冲击回波共振频率计算公式为

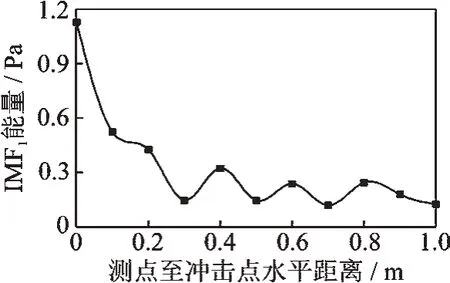
图12 IMF1能量随传播距离变化曲线Fig.12 IMF1 energy variation curve with propagation distance

由图可知，无砟轨道板中冲击回波共振模态的主频约为10 kHz，因此共振模态波的主要成分同样包含在声信号的IMF1中。测点距离增大至0.2 m 的过程中共振模态波成分减少，IMF1能量急剧降低；测点距离大于0.2 m 后IMF1能量在0.3 Pa 浮动，变化幅度趋于平缓，这是因为表面波沿轨道板上表面传播过程中能量衰减较慢。

4.1 数据处理结果分析

分别处理其他工况的计算结果，并定义能量放大系数为各探针声压能量与CA 砂浆层无脱空状态下对应位置探针数据的比值，使脱空特征指标无量纲化。不同工况下的IMF1能量放大系数变化情况如图13 所示。

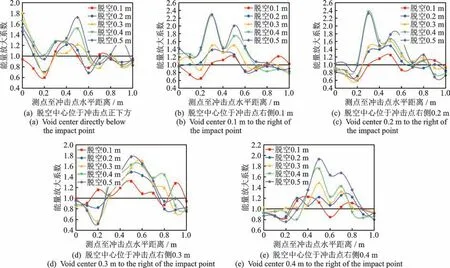
图13 不同工况下IMF1能量放大系数变化曲线Fig.13 Variation curve of IMF1 energy amplification factor under different working conditions

距冲击点0～0.2 m 测点信号主要为共振模态波。当脱空中心位于冲击点正下方或右侧0.1 m 处时，共振模态波IMF1能量放大系数较大，表明共振模态波的IMF1能量能够对冲击点正下方一定程度的CA 砂浆层脱空进行识别。当脱空长度为0.1 m时，共振模态波IMF1能量放大系数均小于1，主要由于纵波传播至脱空两端时出现绕射，导致反射波能量减少，此时共振模态波无法识别CA 砂浆层脱空。

距冲击点0.3～1 m 测点信号主要为漏表面波，对比不同脱空工况下漏表面波IMF1能量放大系数变化曲线可知，当CA 砂浆层发生不同程度脱空时，距冲击点0.3～0.8 m 处IMF1能量放大系数变化幅度较大，且变化量与脱空长度呈正比关系。

随着脱空中心至冲击点距离增大，不同脱空长度下IMF1能量放大系数曲线的峰值位置出现右移，这主要由于脱空中心至冲击点距离较大时，共振模态波IMF1能量放大系数显著减小，而CA 砂浆层脱空处上方轨道板内的反射纵波与反射横波增多，耦合形成的漏表面波IMF1能量增大，从而在曲线上表现为峰值右移。

4.2 基于能量放大系数的脱空参数定量表征

为直观描述能量分布与脱空参数之间的关系，进一步提取能量放大系数曲线线形指标进行脱空的定量表征。

4.2.1 脱空长度与IMF1能量的关系

脱空长度对距冲击点0.3～0.8 m 处测点能量放大系数之和的影响如图14所示。随着脱空长度增大，至冲击点0.3～0.8 m 的IMF1能量总和呈增长趋势，仅当脱空中心位于冲击点正下方时变化规律不明显。

图14 脱空长度对距冲击点0.3～0.8 m 处测点能量放大系数之和的影响Fig.14 Effect of void length on the sum of energy amplification factors of measuring points 0.3～0.8 m away from impact point

4.2.2 脱空位置与IMF1能量的关系

脱空位置对IMF1能量放大系数曲线形心位置影响如图15 所示。其形心定义为

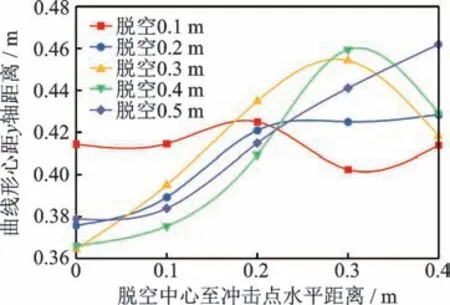
图15 脱空位置对IMF1能量放大系数曲线形心位置影响Fig.15 Effect of void position on centroid position of IMF1 energy amplification factor curve

其中：X为形心；i为测点号数；E为能量放大系数；x为测点至冲击点距离。

本研究采用IMF1能量放大系数变化曲线形心X对上述“峰值右移”程度进行量化，作为脱空位置的特征指标。由图14 可知，当脱空中心至冲击点水平距离小于等于0.3 m 时，脱空位置与IMF1能量放大系数曲线形心X距y轴距离具有正相关关系，仅当脱空长度为0.1 m 时（图中红色曲线）无明显规律，这是因为此时脱空尺寸过小，弹性波传播至脱空缺陷时以绕射为主，反射能量较少，导致识别效果不佳。当脱空中心至冲击点水平距离为0.4 m 时，形心位置变化趋势同样无明显规律，这是由于脱空边缘距离冲击点较远，弹性波反射作用减弱，采集信号中反映脱空特征的能量较少。由此可见，IMF1能量放大系数曲线形心X一定程度上能够对脱空位置进行表征，但适用范围受限。

5 结 论

1）当CRTSII 型无砟轨道板出现脱空时，冲击荷载激励生成的漏表面波在高频段易发生模式变换。高频成分在轨道板传播过程中引起的表面振动位移较大，适合作为脱空特征信号。

2）采用希尔伯特-黄变换对声压信号进行处理，得到的第1 阶本征模函数IMF1中主要包含了高频脱空特征信号，能够反映脱空特征。

3）声压信号的IMF1能量分布与脱空长度、脱空位置之间表现出正相关性，即随着脱空长度增大，距冲击点0.3～0.8 m 的漏表面波IMF1能量放大系数之和呈增大趋势。随着脱空中心至冲击点距离增大，IMF1能量放大系数曲线形心X至y轴距离呈增大趋势，但脱空长度小于0.1 m 或脱空中心至冲击点水平距离大于0.3 m 时，脱空位置对IMF1能量放大系数曲线形心位置影响较小。