“正难则反”一般方法应用实例分析

傅海伦　周方群

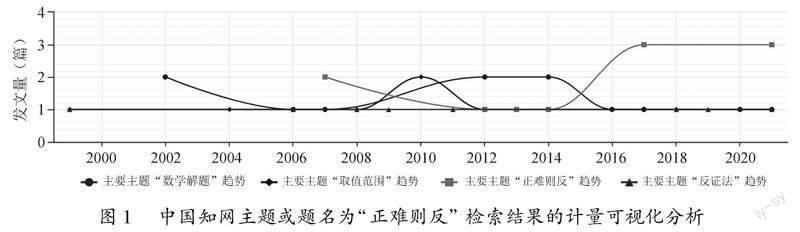
【摘 要】针对目前数学教学中具体解题方法与数学思想方法相脱轨的现象，基于数学方法论的角度，提出重视“正难则反”一般方法的应用，并列举正难则反在函数、几何证明、概率等方面的应用实例分析，从而架构从具体解题方法到数学思想方法之间实质联系的桥梁与纽带，从而达到化繁为简、化抽象为具体的效果.

【关键词】一般方法；正难则反；逆向思维；应用

1 背景与意义

数学结论的教学具有当下意义，数学方法按照抽象程度的不同可分为：具体解题方法、一般方法（逻辑与实验方法）以及在此基础上概括形成的数学思想方法这三个层次［1］.在实际教学中，师生重视具体解题方法的教学，而相对忽视一般方法的教学.

数学方法论的教学要依托一般方法论的理论基础，应立足于数学学科特点和学生的学情，重视一般方法的教学，既要跳出“解题术”的功利教学，又要避免空谈数学思想的低效教学， 从而更有效地实现从具体解题方法到数学思想方法的过渡，

在此基础上，训练学生的思维能力，提高思维品质，提升数学素养.

“数学是思维的体操”.数学依靠其抽象性、严谨性和广泛的应用性的特点，为思维训练提供了良好的现实原型与方法程序.《普通高中数学课程标准（2017年版2020年修订）》提出了包括“逻辑推理”在内的六大核心素养，而逻辑思维能力是各种思维能力的核心［2］.由此可见，数学对人的思维发展具有良好的训练功能和促进效果.因此，學习数学的意义不在于“解题术”的突破，而在于通过解题的训练提升学生的思维品质.而现阶段具体解题方法和数学思想方法相脱轨，或者过于强调解题步骤的规范性，或者在学生知识储备还没达到标准的情况下空谈思想，造成学生迷茫，并没有真正达到思维训练的目的.

例如，在分析法的实际教学中，教师往往根据问题引入分析法这一具体解题方法，并强调方法的步骤规范，进而上升至逆向思维层面.学生在学习新方法新思想时，往往还没领悟到分析法的精髓，就被迫地与逆向思想相联系，并且将具体解题步骤当做学习重点，这造成了学生眼光的狭隘与思想的浅薄.

“正难则反”能很好地架起思想方法与具体解题方法的桥梁，起到过渡与联系作用.随着新时代对人才要求的提升，正难则反愈发受到广大教育研究者的重视.

现阶段的研究对正难则反的内涵界定相对模糊.秦雄伟在《逆向思维在中学数学教学中的应用研究》一文中，将正难则反定义为逆向思维在中学数学教学策略中的应用之一，并与反例法教学策略、补集法教学策略、执果索因教学策略并列［3］.刘晓翠在《数学解题中的正难则反思想及其教学实践研究》一文中将正难则反定义为一种思想，并将逆推分析法、反证法、构造反例以及从反面思考，定义为正难则反思想解题的具体方法［4］.更多学者将正难则反定义为解题策略并着重介绍其在解题当中应用的某几种形式.下面，我们就对几位专家学者和教师的具体研究进行对比分析：

教师讲解是从方法升华到思想，学生应用是借助思想来搜寻解题方法，在学生学习深度没有达到升华至思想的程度时，需要一个比思想抽象程度更低，比具体解题方法更加概括的概念来实现方法的暂时归类储存与后期的衔接过渡.因此，本文立足于逆向思维和悖向思维的培养，重新界定“正难则反”为一种一般方法，并给出其在函数、几何证明、概率、三角函数、不等式等方面的应用实例分析.2 “正难则反”一般方法的内涵解析

逆向思维即“反其道而行之”，指沿固有思路的反向思考问题，反向推导本应证明或求解的结论，使其返回到已知的定理、定义或概念的思维过程［5］.数学方法中的逆推分析法、逆向运算法等，均为逆向思维在数学方法中的具体应用.

悖向思维不同于一般的逆向思维，其立足于认知冲突，从原来认识的反面出发，寻找新的发展可能.相对于内容上的“反”，悖向思维更加强调对立双方间的和谐性，从而消除思维与逻辑的混乱，促进消极混乱到积极明了的转化［6］.数学方法中的反证法、反例法、对立事件法等，均是悖向思维在数学方法中的具体应用.

“正难则反”是一般的方法，属于逻辑与实验方法的范畴.其基本含义是，如果正向或从正面思考和分析问题比较困难，那么就可以反向出发或尝试从问题反面出发分析和解决问题［4］.这种遇难则反的方法，同时囊括了逆向思维和悖向思维的中心思想，是逆向思维和悖向思维指导下的一般的数学方法，下属概念中可以容括逆推分析法、逆向运算法、反证法、反例法等具体数学方法.“正难则反”相对于思维层面，其抽象程度更低，又比具体方法更具有概括性.沈文选教授曾指出“离开了数学解题方法原理的数学思维，只能是杂乱无章的胡思乱想”［7］.正难则反既能高度体现逆向思维的过程性和方向性，又能对悖向思维有“引流”作用，有其独特方法论意义.正难则反作为一般的数学方法，其地位如图2所示：

3 “正难则反”一般方法的应用实例分析

3.1 “正难则反”一般方法在函数中的应用

例1 已知函数f（x）=ax2+xlnx（a∈R）的图象在点（1，f（1））处的切线与直线x+3y=0垂直.

（1）求实数a的值；

（2）求证：当n>m>0时，lnn－lnm>m/n－n/m.

分析 对于本题第一问，可以由f（x）=ax2+xlnx（a∈R），求出f（x）的导数.

f′（x）=2ax+lnx+1，又因为切线与直线x+3y=0垂直，所以切线的斜率为3，所以f′（1）=3，即2a+1=3，故a=1.

对于本题的第二问，题目给出的是一种陌生形式的不等式，难以将其与已知知识联系起来.此时，不妨“反过来”思考，先对要证明的不等式进行逆推分析，寻找使之成立的充分条件，合理变形为熟悉形式，再通过整体代换、构造函数等常规方法证明原式的正确性. 要证lnn－lnm>m/n－n/m，即证lnn/m>m/n－n/m，只需证lnn/m－m/n+n/m>0.此时，不等式的左边已被逆推为具有规律性的式子，提示着解题者应采用整体代换法和构造函数法.

令n/m=x，由已知n>m>0，得n/m>1，即x>1，根据题设提示构造函数g（x）=lnx－1/x+x（x>1），则其导函数g′（x）=1/x+1/x2+1.

因为x∈（1，+∞），所以g′（x）=1/x+1/x2+1>0，故g（x）在（1，+∞）上单调递增.

所以gn/m>g（1）=0，即lnn/m－m/n+n/m>0成立，所以当n>m>0时，lnn－lnm>m/n－n/m.

评注 本题所用的方法是正难则反中的分析法.这种分析法实则为逆推证明，从思维方向上来看，它的论证思考顺序从结论出发，寻求它的论据，直至归结到题设，是直接证明“由因导果”的反向，在逻辑上表现为“执果索因”.

这种分析法虽在思考方向上迂回间接，但是在思维活动中，相对于综合法的发散性，更具有直接的方向性，所以效率往往更高［8］. 另外，从本题来看，正难则反的主要作用体现在提示思路，解题者能经过逆推分析，使陌生结论向已知知识转化，从而使无序的思维更加清晰明了，达到“柳暗花明又一村”的效果.

教师要教会中学生发现本题正向难以入手后，能想到反向，并掌握一定的分析法书写规范与逻辑衔接方法.

3.2 “正难则反”一般方法在几何证明中的应用

例2 如图3，在△ABC中，∠CAB>90°，D是BC的中点.求证：AD<1/2BC.

分析 题设中有两个条件：p1——在△ABC中，∠CAB>90°，p2——在△ABC中，D是BC的中点，结论为q——在△ABC中AD<1/2BC.针对这道题的两个前提条件，我们可以采取“（p1∧p2）→q（p2∧q）→p1”的论证形式，将结论加以否定作为条件使用，使得推出一个与题设矛盾的命题，从而证明原命题的正确性. 假设AD≥1/2BC.下面，可以分为两种情况：

①若AD=1/2BC，则△ABC为直角三角形，即∠CAB=90°，与题设矛盾，舍去.

②若AD>1/2BC，因为D是BC的中点，即DC=BD=1/2BC，所以AD>BD，由三角形大边对大角的性质，在△ADB中∠B>∠DAB.

同理∠C>∠CAD，所以∠B+∠C>∠DAB+∠CAD=∠CAB，又因为∠CAB+∠B+∠C=180°，所以2∠CAB<180°即∠CAB<90°，与题设矛盾.

综上所述，AD<1/2BC.

评注 本题所用的是正难则反中的反证法.反证法是间接证明的一种，当直接证明命题比较困难时，我们从反面出发，将结论否定进行论证，直至推出矛盾，从而确立原命题的真实性.当问题的条件较少，或者问题反面比较具体、情况较少时，常常采用反证法［9］.

本题正难则反的主要作用在于扩充题设条件，利用逻辑冲突的方法，从结论的对立面出发，将思路“引流”到分类讨论上来，是悖向思維与逆向思维的一次完美融合.

教师需要引导中学生学会做出反设，当正面提示较少时，勇于转换思维，从反面入手，把求证作条件，把已知变未知，锻炼学生的思维品质. 3.3 “正难则反”一般方法在概率中的应用

例3 现有红、黄、蓝、绿四色卡片共16张，且每种颜色各四张，从中任取三张卡片，要求它们不能是同一颜色，且红色卡片至多一张的概率是？

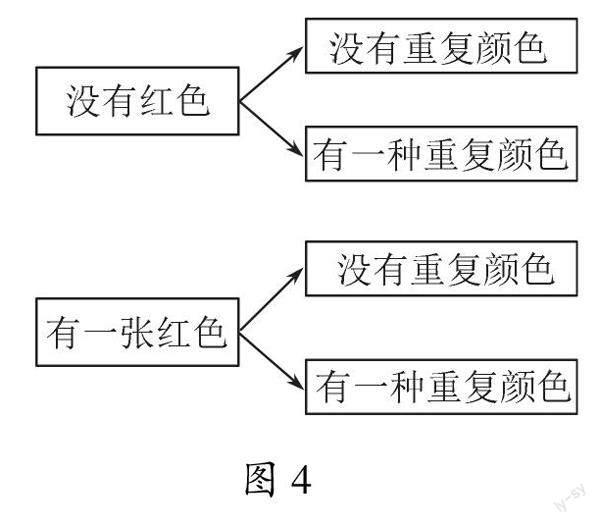
分析 本题若从正面思考，则需综合考虑“有无红色”和“有无重复颜色卡片”两个问题，共分4种情况讨论如图4所示.

而若从反面入手，只需考虑“三张卡片都是同一颜色”和“有两张红色卡片”两种情况：

①任取三张卡片都是同一颜色的取法共C14×C34种；

②任取三张中有两张红色卡片的取法共C24×C112种；

评注 两个对立事件互为反面事件，两者的概率和恒为1.本题充分运用了悖向思维，从事件的反面入手，使问题的复杂性降低，简化思维量与分类情况.正难则反是快速解决本题的关键，也是提高本题正确率的关键所在.

在概率问题中合理运用正难则反的方法，既可将复杂问题简单化，避免情况过多造成的讨论遗漏，也可以让学生感受到反过来想问题的简单性与巧妙性. 4 结论与反思

现代社会重视对思维的锻炼，但是学生在思想转化为具体方法的运用过程中还有一定的困难.因此，数学教师应基于前人对于方法论的研究以及日常的数学教学情况，重视“正难则反”作为一般方法的应用与教学.借助“正难则反”这种一般的方法，可以架构从具体解题方法到数学思想之间实质联系的桥梁与纽带，使得学生可以更有效、更便捷地实现从具体方法到数学思想的过渡，进而促进学生思维发展，减少直接运用思维思考的抽象性与复杂性，从而达到化繁为简、化抽象为具体的效果.同时还可以有效地锻炼思维品质，提高数学能力，提升数学素养.

当然，对于“正难则反”一般方法的具体实践的研究还有待加强.例如，在“正难则反”的实际应用教学中，怎么使得学生正确地理解与运用一般方法，既保证运用的计划性又保障灵活性，特别是，“正难则反”这种“以退为进”的策略，对于数学思维品质培养的有效性以及学生思维发展程度的评判，都需要建立定性与定量的标准.因此，从这个意义上说，之后的研究方向主要集中在立足于学生学情实际，深入探讨数学方法论的教学价值，从培养学生数学核心素养的角度出发，

从实践中进一步探索一般数学方法与学生思维及其发展的深层次关系及其评价，这需要对以往的数学方法教学体系进行重组，并深入教学一线进行实践与分析.

参考文献

［1］章士藻.数学方法论简明教程［M］.南京：南京大学出版社，2006： 2-3.

［2］中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）［M］.2版.北京：人民教育出版社，2020：5.

［3］秦雄伟.逆向思维在中学数学教学中的应用研究［D］.重庆：西南大学，2020.

［4］刘晓翠. 数学解题中的正难则反思想及其教学实践研究［D］.长沙：湖南师范大学，2014.

［5］肖媛元. 初中生数学逆向思维的现状及对策研究［D］.重庆：重庆师范大学，2019.

［6］郑毓信.悖向思维与悖向思维和谐性原则［J］.数学通报，1990（07）：2-3.

［7］沈文选，杨清桃.数学方法溯源［M］.2版.哈尔滨：哈尔滨工业大学出版社，2018：7.

［8］马波.中学数学解题研究［M］.2版.北京：北京师范大学出版社，2017：9.

［9］张安平.反证法——证明数学问题的重要方法［J］.中国城市经济，2010（11）：179.

作者简介 傅海伦 （1970—），男， 教授，博士生导师;主要从事数学课程与教学论研究.

周方群（1998—）女，山东师范大学教育硕士专业学位研究生；主要从事中学数学课程与教学论研究.

基金项目 2021年度山东省社会科学普及应用研究项目“传统数学文化传播与拓展读本”（2021-SKZZ-24）；2022年山东省优质专业学位教学案例库建设（SDYAL2022067）;

山东师范大学优秀教学成果培育项目“专业认证下的数学实践教学创新体系建设研究”（2019PY05）.