数学新高考改革“考教衔接”的衔接方式探讨

【摘 要】在高考已经实现由“以纲定考”到“考教衔接”转变的背景下，通过剖析“考教衔接”中的要素和结构，从与数学课程标准的对标衔接、与教材素材的重点衔接、与高考命题立意的拓展衔接、与高考评价体系的对比衔接等方面，论述了考教衔接的衔接方式，结合高考试题阐述了衔接教学的过程.

【关键词】考教衔接;衔接方式;教材;教学

2022年9月15日，教育部教育考试院院长孙海波在其报告《立德树人、服务选材、引导教学——党的十八大以来高考内容改革进展及成效》中指出，高考内容改革有效引导教学，实现高考由“以纲定考”到“考教衔接”的转变，逐步形成“招—考—教—学”良性互动.这说明“考教衔接”在高考备考和教学中应该引起一线教师高度关注.1 考教衔接的提出背景

2019年以前，每年高考都会有《考试大纲》，教学对照大纲，考什么就教什么，不考的知识点就不教，从而处于“以纲定考”与“以考定教”的时代.2019年6月，国务院办公厅出台《关于新时代推进普通高中育人方式改革指导意见》，指出学业水平选择性考试与高等学校招生全国统一考试命题要以普通高中课程标准和高校人才选拔要求为依据，实施普通高中新课程的省份不再制定考试大纲.2020年1月，教育部考试中心颁布《中国高考评价体系》，提出“一核”“四层”“四翼”，回答了为什么考、考什么、怎么考的问题［1］.《普通高中数学课程标准（2020年修订）》（以下简称课标）的高考命题建议部分指出，命题应依据学业质量标准和课程内容，注重对学生数学学科核心素养的考查，处理好数学学科核心素养与知识技能的关系，要充分考虑对教学的积极引导作用［2］.2022年7月《中国考试》高考数学试卷评价中也指出，加强考教衔接，发挥引导作用［3］.因此，一系列文件的颁布与2021、2022年新高考改革的具体实施都强调了课程标准是教学和考试命题的基本依据，是两者共同的源头和遵循的依据.这也意味着教学与考试之间的关系需要通过高中数学课程标准来衔接与关联，并不是简单的“以考定教”或者“以教定考”关系.2 考教衔接的要素与結构

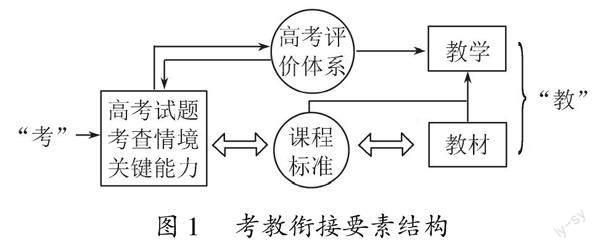
考教衔接中的“考”具体表现在高考试题、考查情境、关键能力等方面，它自然会涉及“考什么”与“怎么考”的要求.那么如何理解考教衔接中的“教”呢？从“考什么就教什么”到孙海波院长提出的“引导教学回归课标、回归课堂主渠道”［4］.因此考教衔接中的“教”既指教学，也指教材.高考体现的是“立德树人、服务选才、引导教学”的核心功能，从而命题专家需要研究的是高考试题、考查情境、关键能力是否在课程标准的范围之内，是否落实了高考评价体系的“四层”“四翼”要求，对教学会产生什么样的影响，因为高三复习教学需要在“怎么考”“考什么”的导向下定位课堂内容和教学方式.同时高考要根据课标要求，体现教材素材，最后作用于课堂教学，从而考教衔接中的“教”离不开课标中课程内容的教学要求与学业要求.因此考教衔接中的衔接要素结构图可呈现如下：

3 “考”与“教”的衔接方式

从考教衔接要素结构图可以看出，作为一线教师或学校主要研究的是从“考”到“教”衔接的方向，要以高考为导向从数学课程标准、高考评价体系两方面去落实教学要求，主要体现在以下四种方式.

3.1 与数学课程标准的对标衔接高考命题的要求为严格依据高中课程标准，确保“内容不超范围，深度不超要求”［4］.这里的范围是指课标中的课程内容，深度要求是指课标中的学业要求.那么复习教学时，要根据高考真题中的能力考查要求，对标教学内容的能力要求，对标知识点考查的学业要求.

试题1 （2022年全国新高考Ⅰ卷20题）一医疗团队为研究某地的一种地方性疾病与当地居民的卫生习惯（卫生习惯分为良好和不够良好两类》的关系，在已患该疾病的病例中随机调查了100例（称为病例组），同时在未患该疾痫的人群中随机调查了100人（称为对照组）得到如下数据：

（1）能否有99%的把握认为患该疾病群体与未患该疾病群体的卫生习惯有差异？

（2）从该地的人群中任选一人，A表示事件“选到的人卫生习惯不够良好”，B表示事件“选到的人患有该疾病”，P（B|A）/P（|A）与P（B|）/P（|）的比值是卫生习惯不够良好对患该疾病风险程度的一项度量指标，记该指标为R.

（ⅱ）利用该调查数据，给出P（A|B），P（A|）的估计值，并利用（ⅰ）的结果给出R的估计值.

本题所体现的是通过统计学去研究事件的独立性，考查的必备知识是2×2列联表与随机事件的条件概率，那么衔接课标内容教学要求体现如下：

3.2 与教材素材的重点衔接

找准了必备知识在课标中的内容要求与学业要求，目的是引导教师做到应教尽教，要从教材的素材中去复习备考、回归教材，引导教师了解这类必备知识教学程度，引导教学把精力放在讲透课程重点内容上［4］.比如例1中的课标内容要求“通过实例，理解2×2列联表的统计意义”的教材素材可以衔接到“人教A版选择性必修第三册126页例1”，“通过实例，了解2×2列联表独立性检验及其应用”的教材素材可以衔接到“人教A版选择性必修第三册132页例2”，具体如下：

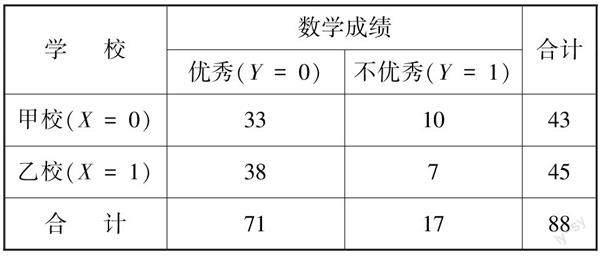
教材素材1 （人教A版选择性必修第三册126页例1）为比较甲、乙两所学校学生的数学水平，采用简单随机抽样的方法抽取88名学生.通过测验得到了如下数据：甲校43名学生中有10名数学成绩优秀;乙校45名学生中有7名数学成绩优秀．试分析两校学生中数学成绩优秀率之间是否存在差异.

教材将样本数据整理成2×2列联表形式，计算并比较相应变量的频率.

衔接教材素材1的目的，是复习中让学生回顾用频率估计概率的思想，要求学生加深理解这种推断方法的合理性及不足，让学生理解“由于样本具有随机性，依据频率所作的判断可能会出错，从而需要教师衔接教材素材2，与独立性检验知识关联，实现课标的学业要求.

教材素材2 （人教A版选择性必修第三册132页例2）依据小概率值α=0.1的κ2独立性检验，分析例1中的抽样数据，能否据此推断两校学生的数学成绩优秀率有差异？

此素材利用独立性检验，零假设为H0：分类变量X与Y相互独立，即两校学生的数学成绩优秀率无差异.根据κ2=88×（33×7－10×38）2/43×45×71×17≈0.837<2.706=x0.1.根据小概率值α=0.1的κ2独立性检验，没有充分证据推断H0不成立，因此可以认为H0成立，即认为两校的数学成绩优秀率没有差异.素材2的结论与素材1中利用频率计算得出的结论不同，目的是让学生体会独立性检验的必要性，同时教师也要注意κ2独立性检验与旧版教材中的区别，真正体现出“教学把精力放在讲透课程重点内容上”.

至于课标学业要求中“理解随机事件的独立性和条件概率的关系”也可衔接到教材选修第三册46页中“当P（A）>0时，当且仅当A与B相互独立时有P（B|A）=P（B）”.

3.3 与高考命题立意的拓展衔接

近几年来高考命题结构的合理性、命题立意的创新性，增强了基于课标理念、回归教材、科学备考的信心，在关注解题的同时引导着更多的教师对高考真题的命题情境、立意进行深入和拓展研究，最后在教學与教材上进行体现.

试题2 （2021年全国Ⅰ卷第8题）有6个相同的球，分别标有数字1，2 ，3，4 ，5 ，6 ，从中有放回地随机取两次，每次取1个球．甲表示事件“第一次取出的球的数字是1”，乙表示事件“第二次取出的球的数字是 2 ”，丙表示事件“两次取出的球的数字之和是8”，丁表示事件“两次取出的球的数字之和是7”，则（ ）.

A．甲与丙相互独立 B．甲与丁相互独立C．乙与丙相互独立 D．丙与丁相互独立

此题的命题立意是考查学生对两个随机事件独立性的理解，需要学生先用概念、性质分析对象的结构特征，确定样本空间和基本事件的个数，通过计算检验P（AB）=P（A）P（B）是否成立来获得答案.那么如何基于此命题立意进行拓展，完成教材定位与教学引导呢？首先是情境的教材定位.关于两个随机事件的独立性，教材上有基本习题（比如人教A版必修第二册248页例1），当然自然而然也会拓展到三个两两独立事件A，B，C同时发生的概率与事件A，B，C的概率的关系，即P（ABC）=P（A）P（B）P（C）是否成立？这个问题在教材有专门的旁白思考.

其次是问题导向的教学引导.P（ABC）=P（A）P（B）P（C）是否成立，主要从三个方面去引导学生完成探究：

第一，A，B，C三个事件两两独立，要通过例题教学说明P（ABC）≠P（A）P（B）P（C）.比如以下课本习题教学：

例1 设样本空间={a，b，c，d｝含有等可能的样本点，且A={a，b}，B={a，c}，C={a，d}.请验证A，B，C三个事件两两独立，但P（ABC）≠P（A）P（B）P（C）.第二，当P（ABC）=P（A）P（B）P（C）时，要通过例题教学说明A，B，C三个事件并不两两独立.比如以下例题教学：例2 一个正八面体，八个面分别标以数字1到8，任意抛掷一次这个正八面体，观察它与地面接触的面上的数字，得到样本空间为Ω={1，2，3，4，5，6，7，8}，构造适当的事件A，B，C，使P（ABC）=P（A）P（B）P（C）成立，但不满足A，B，C两两独立.例2的举例很简单，根据例1的举例方式，可构造A={1，2，3，4}，B={1，3，4，5}，C={1，6，7，8}.

第三，在完成前面两部分的探究后，要给出P（ABC）到底如何计算的一种方式，通过习题教学引出计算P（ABC）的公式.比如：

例3 证明：当P（AB）>0时，P（ABC）=P（A）P（B|A）P（C|AB）.

教学中，例3的证明过程与试题1中R的证明方法类似，证明之后据此引导学生计算P（A1A2…An）的计算公式.

到这里之后，对课标中“理解随机事件的独立性和条件概率的关系”的要求，才算从教学上基本完成.

3.4 与高考评价体系的对比衔接

高考评价体系是高考命题、评价与改革的理论基础和实践指南［1］，在高考评价体系的研读对象中明确指出了要求广大师生学习参考使用.另外，在高考命题的实施过程中，“四翼”是联结“四层”高考考查内容与高考命题实践的纽带.那么一线教师必须深入学习《中国高考评价体系》，从“四翼”的角度，也即“怎么考”的角度进行对比衔接教学.

首先，要从“基础性”来把握数学学科内容“四基”.数学学科基础知识、基本技能、基本方法、基本活动经验是夯实数学基础性、通用性以及情境典型性的载体.比如数学基本方法中配方法、换元法、消去法、割补法、反证法、待定系数法等具体方法在解题或教学中都随处可见；分析与综合、归纳与演绎、比较与类比、具体与抽象、一般与特殊等常见逻辑方法是培养学生六大数学核心素养的基本措施.

其次，要从“综合性”来处理知识融合与教学的关系.高考试题综合性不仅针对数学学科内容的交汇，还包括情境的复杂性，比如数学学科内部的知识交汇以及与自然科学、社会科学的内容和情境的综合交汇.要引导学生深入挖掘我国社会经济建设和科技发展等方面的学科素材，引导学生关注我国社会现实与经济、科技进步与发展以及优秀传统文化［5］.

再次，要从“应用性”来思考教学与解题的关系.应用性在生活实践情境或学习探索情境中，迁移学科所学内容、解决实际问题，在数学学科中体现在题目形式、解题方法、数学思维方式上，体现一定的创新.目前，很多学校的高考备考教学，其实就是解题、刷题的教学.近两年新高考的实践表明，高考已经实现了由“解题”到“解决问题”的转变，高考命题秉承的是“价值引领、素养导向、能力为重、知识为基” 的综合考查模式，考查的重点是学生思维和解决问题的能力［4］.因此加强提升“问题解决能力”教学的探讨及加强信息技术在教学中的应用探讨，才能把对“应用性”理解不仅仅定位在解题上.

最后，从“创新性”来提升教学中情境处理与数学建模能力.创新性要求学生在真实情境中对一些生活现象、生产问题或社会热点问题，通过信息提取与数学转化，完成开放性或探究性的任务.高考数学创新性考查要求的落实要创新情境型材料的选取思路、情境化试题的呈现形式和情境活动的预设方式，致力于学生数学知识或方法即用、知用和善用能力发展水平的检测［6］，而在数学学科的四大主题中“数学建模活动与数学探究活动”最容易体现出创新性，因此，要将高考试题中体现的数学模型（函数模型、不等式模型、方程模型、概率模型等）、创新情境型材料（如新概念题、跨学科融合、生活情境素材）、创新情境化试题的呈现形式（举例问题、劣构问题、存在问题等）、创新情境活动的预设问题（方案设计等）等体现在解题教学中.

4 结语随着新高考改革的持续深入，“考教衔接”将是一个学校不可回避的话题，必将统筹到整个备考的规划与策略当中，也必将与大单元教学、作业设计、微专题设计等热门话题关联.为了更好地教学与备考，教师一定要从学生实际出发，开展学情调研，及时开展联考数据分析，根据“教”与“考”的衔接方式及时制定和调整科学的考教衔接策略.

参考文献

［1］教育部考试中心.中国高考评价体系［M］. 北京：人民教育出版社，2019.

［2］教育部.普通高中数学课程标准（2017年版2020年修订）［M］. 北京：人民教育出版社，2020.

［3］教育部教育考试院.创设情境，发挥育人作用；深化基础，考查核心素养——2022年高考数学全国卷试题评析［J］.中国考试，2022（07）：14-19.

［4］王辉，孙海波，李晓勇，等.考试招生制度改革这十年［J］.中国考试，2022（10）：4-6.

［5］教育部教育考试院.聚焦核心素养考查关键能力——2021年高考数学全国卷试题评析［J］.中国考试，2021（07）：70-76.

［6］柯跃海.高考数学创新性考查要求的落实路径探析［J］.中国考试，2021（01）：69.

作者简介 周威（1985—），男，湖南邵阳人，中学一级教师;研究方向为中学数学教育与评估研究;发表论文80余篇，出版专著1本；主持多项省级、市级课题.