探讨“问题提出”教学的一般模式——基于“乘法分配律”的课堂分析

许天来，蔡金法

探讨“问题提出”教学的一般模式——基于“乘法分配律”的课堂分析

许天来1，蔡金法2

（1．广州大学 数学与信息科学学院，广东 广州 510006；2．特拉华大学 数学系，特拉华 纽瓦克 19716）

结合“乘法分配律”的课堂实例探讨“问题提出”教学的一般模式，包括：（1）教师呈现问题情境；（2）教师根据教学目标设置恰当的引导语；（3）学生以个体方式或小组方式提出问题；（4）师生对学生所提问题进行“分析”“选取”“排序”和“求解”．一节课可能包含多个类似的问题提出教学活动．尽管“乘法分配律”的课堂设计远早于问题提出教学一般模式的呈现，但是该课例很符合此一般模式．研究表明了研究和实践的交互作用：通过研究问题提出的一般模式指导问题提出教学，同时问题提出教学的实践促进了一般模式的研究．

问题提出；教学模式；引导语；乘法分配律；P-PBL

1 问题提出

数学问题提出（Mathematical Problem Posing）的研究在过去几十年得到了较大的发展[1]．然而，问题提出融入数学课堂远未实现常态化．当前关于问题提出教学研究的关键问题在于如何帮助教师更好、更多地将问题提出整合到课堂教学．除了要不断进行培训以提高教师运用问题提出进行教学的信念，更重要的是要对问题提出教学的一般模式进行探讨，帮助教师理解问题提出教学的过程，增加其运用问题提出进行教学的信心和实践．

2 研究框架

蔡金法基于对运用问题提出进行数学教学的研究，总结出基于问题提出的教学模式（Problem-Posing-Based Learning instructional model，P-PBL教学模式）[2]，如图1．此模式描述了用单个问题提出任务进行教学的流程，详见文[2]．步骤1和步骤2通常是同时呈现的，但在这个模式中将其分开讨论，是为了强调在设计问题提出的教学任务时，问题情境和引导语同样重要．首先，教师呈现问题情境，这个情境可以是数学情境、生活情境以及其它情境（如科学实验情境或体育情境）[3-5]．其次，在呈现问题情境的同时，应当根据教学目标设置恰当的引导语，对学生所提问题的数量、难度、所涉及的知识领域等提出具体的要求．比如：（1）提出能够对你的同学或老师有一定挑战的数学问题；（2）提出涉及百分比的数学问题；（3）提出3个数学问题，简单、中等难度和较难的各一个；（4）提出尽可能多的数学问题；（5）模仿范例中的问题，提出类似/不同结构的问题；（6）你能提出哪些至少包含2种运算的数学问题；（7）提出现实生活中能用此方程求解的数学问题；（8）提出两个能用加、减法解决的数学问题，并让黑板上的3个数同时出现在你的问题里[5]．再次，学生根据教师设置的情境和引导语，可以自己提出数学问题，也可以在小组中自己先提出数学问题，与组内同学交流与辩论，然后以小组的形式推选出最具代表性、最好的若干问题．最后，师生对学生所提问题进行恰当地处理，主要包含以下4个环节：（1）师生分析学生所提问题，包括对问题进行纠错与完善，以及对重复、无序的问题进行分类；（2）选取难度适中、契合教学目标的问题；（3）确定求解问题的顺序；（4）求解问题．

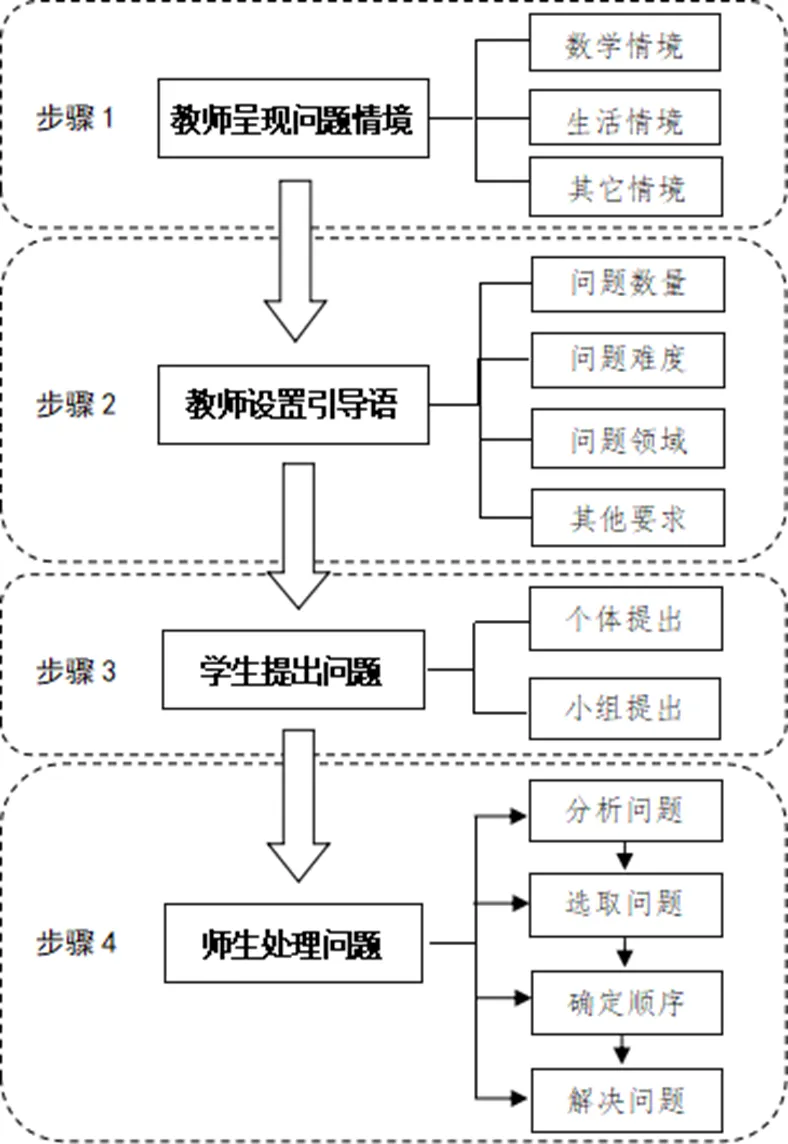
图1 基于问题提出的教学模式

需要指出的是，一节课可能包含多个问题提出的教学活动，对应的课堂上亦会经历多个类似的教学流程．莫延安和王涛在上述研究的基础上，结合多个小学数学教学实例对其中的教学步骤进行了详尽解读[5]．研究结合基于问题提出进行教学的一个具体课例，对如何更好地运用这一教学模式展开进一步的论述．蔡金法等提出了教学理论和教学实践的双向关系[6]．其中，为了教学的理论（theory for teaching）是指旨在为学生创造更多更好的学习机会提供指导的理论；为了理论的教学（teaching for theory）是指通过教与学不断地为提升和发展理论提供素材．如果说为了教学的理论指的是为了更好地教学和促进学生学习的理论，那么为了理论的教学则指的是有意设计用于生成、阐述和测试理论的教学．研究旨在强调教学理论与教学实践间的双向关系的重要性．

3 研究对象

研究对象为小学数学特级教师丁老师2016年基于问题提出教学“乘法分配律”的课例[7]．此课例在大型优质课评比活动中获得一等奖，是丁老师在特拉华大学蔡金法的建议和指导下，勇于突破教学舒适区，克服对失去课堂掌控的恐惧，从零开始深入学习，掌握基于问题提出的教学方法并首次基于问题提出进行的教学尝试[8]．整体教学过程如表1．

表1 “乘法分配律”总体教学过程

可以看出，课例可划分为5个环节，具体为创设悬念、问题提出、点子图、探索归纳和练习回顾．第一，设置悬念，引导学生思考为何丁老师算得这么快．第二，要求学生根据算式提出生活中的数学问题，帮助他们从这些数量众多的、来自“自己的”例证中初步感受乘法分配律的合理性．这种解决“自己的”问题，加上小组“竞赛”的气氛，能很好地调动学生学习的积极性．在解决问题的过程中，引发学生产生连续、愈加强烈的认知冲突——“为什么两种形式的算式可用以解决同一问题？”“为什么两种形式的算式可用以解决所有问题？”第三，结合“点子图”，帮助学生将具有“分”“合”特征的算式联想成自己所提出的数学问题，促进学生通过数形结合理解乘法分配律．第四环节则通过让学生补充等式，引导其从特殊到一般验证规律，结合符号进行归纳．最后，精心设计习题，呼应前文疑问，总结全课．

综上所述，丁老师的课例仅包含一个问题提出活动．下面将结合此课例具体的教学片段，探讨“问题提出”教学的一般模式．

4 研究结果和讨论

4.1 关于教师呈现问题情境

第一个流程和第二个流程往往是同时呈现的．P-PBL教学模式将它们分开，是为了强调在运用问题提出进行教学设计时，情境和引导语同等重要．

【教学片段1】

师：咱们班的同学个个都是编题高手，现在把难度升级，如果只给你算式，你能根据算式提出生活中的数学问题吗？

生：能！

师：谢谢你们自信的回答．这样吧！丁老师把全班分成两大组，第1、2组的同学请根据“算式1”，第3、4组则根据“算式2”，来提出现实生活中的数学问题并清楚地记录下来．（老师故意把两个算式隐藏起来，不让第1、2组和第3、4组的同学分别知道对方的算式．）

学生活动：第1、2组编：(5+7)×4；第3、4组编：5×4+7×4．

评析：运用问题提出进行教学，首先应选择恰当类型的任务情境引导学生提出数学问题，主要分为数学情境、生活情境和其它情境，教师可根据不同的学情和教学目标选取不同类型的情境．数学情境包括算式、方程、几何图形、表格、函数图象、模式（满足特定规律的一组数字或图形，如斐波那契数列和三角点阵）等．教师可要求学生根据“纯”数学情境（如算式和方程）提出生活中的问题，以此帮助学生结合熟悉的生活场景探究抽象的数学知识．生活情境则体现了数学在现实中的运用，贴近学生日常生活实际，具有一定的趣味性．要求学生根据生活情境提出数学问题，可以帮助他们从熟悉的场景中提炼数学关系．其它情境包括科学实验情境和体育情境等学生相对陌生的场景．

在丁老师的教学片段一中，算式“(5+7)×4”和“5×4+7×4”均是“纯”数学情境，相比教师直接给出问题让学生求解，这种学生“自己的”问题更贴合其生活实际，学生可以结合生活中的所见所闻探究抽象的乘法分配律，教师在此基础上展开教学能更好地帮助学生理解所学内容．

4.2 关于教师设置引导语

在上述教学片段一中，丁老师设置的引导语为：“提出现实生活中的问题”，并未提出其它要求．一方面是因为数学表达式的“结构较为稳定”，另一方面是因为教学的重点在于帮助学生理解两种形式的算式均可用以求解同一问题．在其它情境如“斐波那契数列”中，如若不通过引导语进行限制，学生可能会为了追求数量而未能集中精力进行更高层次的思维参与．因此，教师可以设置以下引导语：“（已知数列1，1，2，3，5，…，此数列前两项为1，从第三项开始，每一项都等于前面两项之和）你能根据这个情境提出一个简单的数学问题、一个中等难度的数学问题和一个较难的数学问题吗？”

由上可知，设置问题提出的任务包括问题情境类型的选取以及引导语的设计两个方面．因此，为了更好地设置问题提出任务从而为学生提供更多的学习机会，教师在备课阶段应对学生可能会提出的问题进行预测．首先，教师自己应当能提出尽可能多的、不同类型的数学问题，这有助于教师更好地预测学生可能会提出的正确问题，从而选择恰当的情境类型进行教学．在这个课例中，算式情境是一种“结构较为稳定”的情境，教学实践表明，学生所提问题总体上在丁老师的预料范围内．

其次，教师还应当能较好地预测学生可能会提出的数学问题，包括正确的、错误的数学问题甚至是非数学问题，以进行针对性的教学准备．研究表明，中国教师在预测学生所提问题的准确率上存在着极大的个体差异（7%～89%）[9]．对于具体的问题提出任务，可以通过问卷的形式收集尽可能多的师生所提问题，尤其应注意选取同年龄段、学情相近的学生作为调查对象．如此才能更好地预测学生可能会提出的问题，在备课阶段提前准备应对策略．在有了充分的准备后，如若学生在课堂上提出教师课前未预料到的数学问题，后者可以有更多的时间思考处理对策．

4.3 关于学生以个体形式或小组形式提出数学问题

教师在呈现问题情境并设置引导语后，学生开始提出数学问题．

【教学片段2】

师：刚才同学们都讨论得很热烈，编得很起劲．下面哪个小组来展示一下你们组编的数学问题．

展示第3、4组根据5×4+7×4编的部分数学问题（如图2所示）．

师：请一位小组长来读读你们组编的数学问题．（生读上述“买牛奶问题”．）

小组长（故作神秘）：我请坐在第1、2组的同学来猜猜看，我们是根据哪一道算式来编的？

生1：(5+7)×4．

生2：我认为是5×4+7×4．

师（追问）：真是奇怪了，刚才有的同学猜的却是(5+7)×4，这到底是怎么一回事？谁来说说其中的道理？

生3：(5+7)×4是先算“一瓶普通牛奶和一瓶脱脂牛奶的价钱是12元”，再乘4，就可以算出“各买4瓶共花的钱”；而5×4+7×4是先分别算出“4瓶普通牛奶的价钱”和“4瓶脱脂牛奶的价钱”，再把它们加起来，都是一样的．

生4：我还发现，它们的得数也是相同的，这两个算式都可以解决刚才这个小组编的数学问题．

师：原来如此！

图2 学生提出的数学问题

评析：P-PBL教学模式的第三个流程为学生以个体方式或小组方式提出数学问题．学生可以在小组中先自己提出数学问题，与组内同学进行交流与辩论，以小组的形式推选出最具代表性、最好的若干问题．以小组为单位，课堂所解问题隶属更多学生，小组间的良性“竞争”能较好地激发学生学习的主动性．在小组讨论的过程中，学生不仅进行了个人积极的主动建构，还参与了社会性的沟通过程，有助于达成更有意义的学习[10]．教师也可以让学生自己提出数学问题，从而在有限的课堂时间内留给学生更多独立思考的时间．

在此课例中，丁老师将学生分成两大组，分别根据乘法分配律两种不同形式的算式之一编制问题．在此基础上丁老师要求每组学生通过讨论交流，在规定时间内提交最好的几个问题，因此，不同水平的学生都能充分参与到问题提出活动之中．值得注意的是，在此课例中，并不知道学生是如何根据算式提出数学问题的．

此外，丁老师通过分组“竞争”的形式促进学生积极思考．在第1、2小组学生中，至少猜中1种算式的学生包含以下4种情形．第一，未发现此问题可用给定算式(5+7)×4进行求解，自行得到另一算式5×4+7×4；第二，发现此问题可用给定算式进行求解，未进行其它思考．第三，发现可用给定算式求解，但由于小组之间的“竞争”关系，认为教师不会给两个小组同一算式，通过积极的思考仍未能想出另一算式．第四，发现可用给定算式求解，最终通过积极的思考得到另一算式．无论何种情形，在教师让学生结合生活情境做出解释后，都能引发学生产生强烈的认知冲突：“为什么两种形式的算式都可用以解决同一问题？”特别对于后两类学生，他们在此之前已进行了积极主动的思维参与．相比直接求解教师提供的问题，运用问题提出进行教学的这部分学生寻求第二解法的意愿更为强烈．

4.4 关于师生处理问题

课堂上师生应对学生所提的数学问题进行恰当的处理．

【教学片段3】

前略，与上述片段类似，仅仅是两个小组提问与猜测角色的互换．

师（小结）：虽然这两个算式“长”得不一样，但都可以同时解决这个数学问题（一套书上册5元，下册7元，小明买了4套，一共花了几元？）．千金难买回头看！刚才你们小组编的数学问题，是不是都可以用黑板上的这两个算式来解决？

（给学生一点时间去静静地观察和思考．）

生（齐答）：是的．

师：哇！看来这两个算式真的很神奇．丁老师有一个图更神奇，它可以把大家编的数学问题全部都表示出来，信不信？（学生半信半疑）

评析：丁老师点评学生所提问题，包括表达是否简洁准确、是否符合生活实际等．她让两个小组提问与猜测的角色进行互换，由于有前面教学的铺垫，第3、4组学生很容易发现第1、2组学生所提问题同样可根据两个算式进行编制．教师进而通过追问的方式引导学生思考：“这些问题是不是都可以用黑板上的两个算式来解决？”以此激发学生产生认知冲突：“为什么两种形式的算式均可用以解决所有问题？”很自然地过渡到第三环节的教学——通过点子图帮助学生更好地理解乘法分配律．结合此前第3、4组展示和第1、2组猜测的教学处理，这种连续的、愈发强烈的认知冲突，能提供学生更多的学习机会，更能调动学生积极主动的思维参与．

5 结论

“问题提出”教学的一般模式有助于教师更好地了解如何运用问题提出进行教学，从而提高其教学信念，最终促成问题提出教学更多、更好地融入到数学课堂，为学生提供更多的学习机会．蔡金法和他的合作者认为，尽管现有的多个小学教学案例（包括此文中的案例）充分验证了P-PBL教学模式的有效性[11-13]，但仍需结合更多的案例对其进行验证、细化和修改[2]．另一方面，这一教学模式也可作为教师开发P-PBL教学案例的理论指导．结合P-PBL教学模式发现，教师学习运用问题提出进行教学应从学习设置教学任务开始，包括问题情境的类型与引导语．此为教师引导学生提出问题和随后师生处理问题的基础．

最后需要说明的是，运用“问题提出”进行教学，并不是要取代基于“问题解决”的教学等传统手段，而是作为一种创新，通过恰当的问题提出活动更好地激发学生学习数学的兴趣，引发其产生强烈的认知冲突以突破教学重难点，最终帮助学生达成对数学知识的概念性理解．当教师在教学设计阶段判断出基于问题提出的教学方式也许能为学生提供更多的学习机会，则可以大胆付诸实践，做探究型教师．

[1] 贾随军，姚一玲．问题提出的回顾与展望——美国特拉华大学终身教授蔡金法访谈录[J]．教学月刊小学版（数学），2021（10）：8-13．

[2] CAI J. What research says about teaching mathematics through problem posing [J]. Éducation & Didactique, 2022, 16 (3): 31-50.

[3] 蔡金法，许天来．数学问题提出的例子、类型和内涵[J]．小学教学（数学版），2019（7-8）：34-40．

[4] CAI J, HWANG S. Making mathematics challenging through problem posing in the classroom [M] // LEIKIN R, CHRISTOU C, KARP A, et al. Mathematical challenges for all. New York: Springer, 2023: 115-145.

[5] 莫延安，王涛．小学数学“问题提出”教学步骤解读[J]．教育研究与评论（小学教育教学），2023（2）：59-66．

[6] CAI J, HWANG S, MELVILLE M, et al. Theory for teaching and teaching for theory: Artifacts as tangible entities for storing and improving professional knowledge for teaching [M] // PRAETORIUS A K, CHARALAMBOUS C Y. Theorizing teaching: Current status and open issues. Cham: Springer, 2023: 225-251.

[7] 丁玉华，曾令鹏．“乘法分配律”教学实录与评析[J]．小学数学教育，2017（21）：43-46．

[8] CHEN T, CAI J. An elementary mathematics teacher learning to teach using problem posing: A case of the distributive property of multiplication over addition [J]. International Journal of Educational Research, 2020 (102): 101 420.

[9] XU B, CAI J, LIU Q, et al. Teachers’ predictions of students’ mathematical thinking related to problem posing [J]. International Journal of Educational Research, 2020 (102): 101 427.

[10] 蔡金法，姚一玲．数学“问题提出”教学的理论基础和实践研究[J]．数学教育学报，2019，28（4）：42-47．

[11] ZHANG H, CAI J. Teaching mathematics through problem posing: Insights from an analysis of teaching cases [J]. ZDM, 2021, 53 (4): 961-973.

[12] 陈婷，徐红，徐冉冉，等．数学教师学习使用“问题提出”教学法的个案研究——以“用字母表示稍复杂的数量关系”为例[J]．数学教育学报，2019，28（2）：7-12．

[13] 徐冉冉，裘晓丽，姚一玲，等．基于教师—研究者伙伴关系的初中数学教学改进——以“一次函数”“问题提出教学”为例[J]．数学教育学报，2021，30（1）：25-31．

Exploring the Problem-Posing Based (P-PBL) Instructional Model——An Analysis of a Teaching Case Involving the Distributive Law of Multiplication over Addition

XU Tian-lai1, CAI Jin-fa2

(1. School of Mathematics and Information Science, Guangzhou University, Guangzhou Guangdong 510006, China;2. The Department of Mathematics, University of Delaware, Delaware Newark 19716, USA)

Using a classroom example of a problem-posing teaching case involving the distributive law of multiplication over addition, this study discusses the general pattern of problem-posing instruction. The pattern includes the following steps: (1) The teacher presents a problem-posing situation; (2) the teacher provides a problem-posing prompt along with the problem situation, that is, sets up the appropriate guiding language according to the teaching objectives; (3) the students pose problems either individually or in groups; and (4) the teacher and students analyze, select, sort, and solve the problems posed by the students. A single class session might encompass multiple instances of similar problem-posing instructional activities. Although the lesson involving the distributive law of multiplication over addition predates the formal presentation of the general problem-posing instructional pattern, the example aligns well with this pattern. This paper further underscores the interplay between research and practice: Research on the general pattern of problem-posing instruction guides its implementation whereas the practical application of problem-posing instruction advances research on the general pattern.

problem posing; teaching model; problem-posing prompt; distributive law of multiplication over addition; P-PBL

G623.5

A

1004–9894（2023）05–0017–04

许天来，蔡金法．探讨“问题提出”教学的一般模式——基于“乘法分配律”的课堂分析[J]．数学教育学报，2023，32（5）：17-20．

2023–08–21

西南大学引进人才计划项目（SWU118118）

许天来（1990—），男，广东博罗人，博士生，主要从事数学教育研究．蔡金法为本文通讯作者．

[责任编校：张楠、陈隽]