小学生批判性思维倾向与问题提出表现的现状及相关性研究

唐瑜君，宋乃庆，蔡金法

小学生批判性思维倾向与问题提出表现的现状及相关性研究

唐瑜君1，宋乃庆2，蔡金法3

（1．四川省双流中学，四川 成都 610299；2．西南大学 数学与统计学院，重庆 400715；3．特拉华大学 数学系，特拉华 纽瓦克 19716）

批判性思维倾向、问题提出与创造力有密不可分的关系，是创新教育的关键抓手．以随机选取260名五年级小学生为研究对象，基于已有研究开发“小学生平均数问题提出测试卷”和“小学生数学批判性思维倾向量表”，从多方面探究了小学生批判性思维倾向与问题提出表现的现状以及两者之间的相关性．研究表明小学生批判性思维倾向较好，7个子维度表现由强到弱分别为：开放性、求知欲、成熟度、分析性、自信心、求真性、系统性；小学生具有一定的问题提出表现，超过一半的回答为合理且可解的数学问题，但是问题的扩展性和创新性还需进一步提升．两者整体呈中度正相关性，批判性思维倾向越强的小学生问题提出表现越好，而问题提出表现越好的小学生批判性思维倾向也越强，这为提高学生批判性思维和问题提出能力打开了新路径，为创新意识的培养注入了新思路．

批判性思维倾向；问题提出；小学生；相关性

1 问题提出

如今，世界技术革命浪潮愈发汹涌，科技引领时代，创新决定发展；培养人们创造意识、批判意识等高阶思维能力成为各国教育的核心议题[1]；《21世纪技能框架》把创造力纳入21世纪人才应具备的核心技能[2]；《全民科学素质行动规划纲要（2021—2035年）》中，习近平总书记提到科学创新、科学普及是实现创新发展的两翼[3]．由此可见，创造性人才的培养是中国重要战略目标．教育作为造就富有主体精神和创造力的人的关键部分[4]，是智能时代人才的孵化器．因此，如何利用教育培养创造性人才，是教育研究改革的关键，作为理科基础的数学，更应重视创新教育．

爱因斯坦曾说，提出一个问题往往比解决一个问题更为重要，提出问题需要富有创造力的想象[5]；托兰斯将问题提出作为评价学生创造力的重要指标之一[6]．在社会、数学、科学等领域中，问题驱动其发展．例如，指引20世纪数学发展方向的最高纲领是著名的希尔伯特23问；再如，2020年5月，美国国家研究理事会提出的12个问题是指导未来地球科学研究发展的重要纲领[7]．如此表明问题提出是创造力不可或缺的部分．21世纪教育改革运动也提出批判性思维与创造力具有关联性，批判性思维的发展可带动创造力的提升[8]．已有研究发现问题提出与批判性思维具有一定的关联性．1970年，保罗·弗雷尔在其著作《被压迫的教育学》中将“问题提出教育”作为强调批判性思维的隐喻[9]；2010年，纳尔顿和李针对大学课程设计了基于市场营销和英语的问题提出活动，进行了为期一学期的实验，通过学生在批判性思维作业中获得的学习经验，发现培养学生问题提出能力的过程可以促进其批判性思维的发展[10]；英格利希以五年级小学生为研究对象设计实施了为期一年的问题提出活动计划，通过对前后测的访谈数据及活动课程中过程性数据进行分析发现，当学生提出自己的问题时，他们可以通过探索对具体数学概念的好奇心来增强他们的数学知识，并通过要求学生批判性地评估提出的问题，以此来帮助学生提高对问题结构和问题情境的认知[11]；问题提出式教育通过克服权威主义和理智主义，可以最大化地培养学生分析能力、实践能力与创造能力[9]．由此在一定程度上反映出问题提出活动不仅需要批判性思维的参与，还可作为批判性思维的发展工具．综上所述，问题提出与批判性思维皆与创造力有关，且可从文献中发现批判性思维倾向与问题提出具有一定的关联性．

再者，中国当代教育名家顾明远提出：“新世纪的教育要求学生独立思考，敢做敢想，勇于思考，不会提问的学生不是一个好的学生．”[12]联合国教科文组织要求小学生应具有批判性思维[13]，小学阶段正是培养批判性思维的有利时期[14-15]．根据法乔恩的研究将批判性思维分为技能和倾向，其中批判性思维倾向对于一个人批判性思维发展是不可或缺的，如果一个人没有其意愿，那么能力对他来说则没有意义[16]．《义务教育数学课程标准（2022年版）》不断强调培养学生问题提出能力，以及学生的好奇心、求知欲、质疑精神等批判性思维倾向[17]．然而，徐斌艳研究发现中国数学教育不重视学生问题提出的培养，使得学生缺乏数学批判性和创新性等思维能力[18]．

研究立足数学学科背景下批判性思维倾向与问题提出表现的相关性研究，旨在了解小学生整体和城乡两地问题提出表现及批判性思维倾向的现状，探究两者之间的相关性．研究这些问题不仅能更多地了解问题提出和批判性思维的关系，更重要的是为问题提出作为抓手在数学课堂上培养学生的批判性思维作基础；为培养小学生批判性思维提供指导和建议，为小学生问题提出能力的培养研究提供理论基础，为传统型教学转向创新型教学提供必要的教育策略与指导方法．

2 研究设计

2.1 核心概念界定

2.1.1 数学问题提出

数学教育界对问题提出的理解分为作为认知活动的问题提出、作为教学手段的问题提出以及作为教学目标的问题提出[9]．研究将其作为一种相对独立的数学认知活动，并根据时间顺序，确定为发生在问题解决之前的问题提出，同时，基于研究对象采用学生视角的问题提出，包括：学生基于给定的问题情境提出数学问题，这些情境可能包括数学表达式或图表；学生通过改编已有问题来提出新的数学问题．因此，研究将问题提出概念界定为学生在已有经验的基础上，根据或改编原有情境提出正确的数学问题[19]．

2.1.2 批判性思维倾向

批判性思维倾向是学生发展批判性思维的关键要素，是一种基于情感方面的习惯与态度，其理论内涵纷繁复杂．研究以法乔恩提出的理论为基础，以“加利福尼亚批判性思维倾向问卷”（California Critical Thinking Disposition Inventory）为参照，将批判性思维倾向划分为以下7个维度：（1）求真性：在任何情况下，勇于提问，不会因为个人偏见或权威而放弃对真理的探究；（2）开放性：对不同的观点持宽容态度，允许他人表达自己的意见，不因偏见而回避真相；（3）分析性：在解决问题的过程中，可以找到关键所在，在论据的框架内有逻辑地进行推理分析；（4）系统性：厘清自己的思路，尽可能多地寻找相关信息，有组织、有计划地解决问题；（5）自信心：指对自己的理性分析能力有把握，对自己做出的推理和判断有充足的信心；（6）求知欲：对知识有了解清楚的强烈愿望，即使没有立即反馈的价值，也想要更深入地了解学习；（7）成熟度：指学生能够以谨慎理性客观的态度看待问题，明白问题的复杂性，明白解决问题的方法可能有很多[20]．

2.2 研究对象

研究抽取四川省成都市和四川省偏远山区两所样本学校（城市、乡村各一所）共279名学生，先后在规定时间内完成测试卷一、二（“小学生‘平均数’问题提出测试题”和“小学生数学批判性思维倾向量表”），两所学校均使用北师大版小学数学教材，且教学进度一致．将在规定时间内完成两份测试卷的视为有效数据，回收有效问卷260份，测试卷有效率93%．学生基本情况如表1所示．

表1 研究样本信息表

注:其中学校所在地区编码为C，所在班级编码为B，例如：城市小学1班，编码为C1B1．

2.3 研究工具

2.3.1 批判性思维倾向量表

批判性思维倾向研究工具选取裴昌根团队开发的“小学生数学批判性思维倾向量表”[21]，维度分布如表2．此量表基于CCTDI和CTDI-CV结合数学学科背景改编而成，采用5点式李克特量表记分法，从“非常不同意”到“非常同意”，题目语言设计结合小学生阅读理解水平，并设置了符合小学生日常数学学习的情境，其科学性和可靠性都采用标准的统计方法进行验证，内容效度已通过专家评审达到要求．将所收集的数据运用SPSS分析得到量表信度良好（=0.840）．最后采用AMOS20.0软件进行验证性因素分析，得到各项评价指标如下：/=1.588，=0.047，=0.856，=0.900，=0.901，数据表明量表具有良好的结构效度．

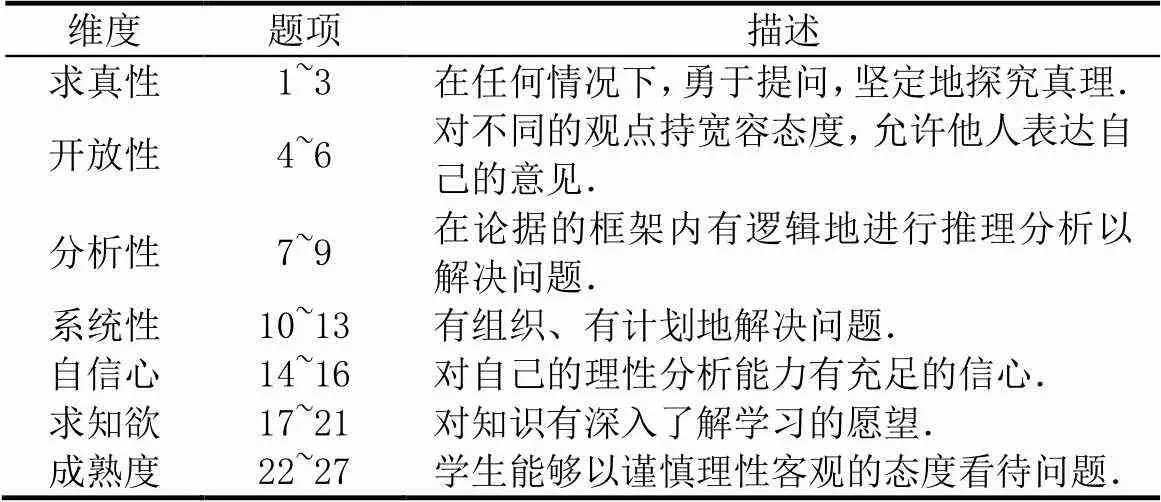
表2 批判性思维倾向量表维度分布情况

2.3.2 小学生平均数问题提出测试卷

“问题提出”测试工具的完成，得益于前人成熟的研究理论．姚一玲等人发现提出的数学问题是否有价值与理解程度有关[22]；胡睿在研究问题提出与问题解决的关系时，将研究工具测试题聚焦于“平均数”，从问题解决出发编制研究工具[23]．因此，问题提出测试工具根据蔡金法“平均数”理解模型从成熟的工具中选择4个问题解决测试题，再结合中国小学生语言特征，改编成符合中国小学生认知思维理解的问题提出测试题，并要求学生根据所给情境提出简单、中等难度、较难的平均数问题，其题目分布结构如表3所示．

2.4 数据分析框架的构建

2.4.1 问题提出表现评价框架

问题提出表现评价标准以刘启蒙和蔡金法所开发的评价框架为理论基础[24]，具体如表4所示．

结合测试题特征和学生实际作答情况，综合多项研究中的评价理论，在专家指导下修改评价框架．主要有3点改变：（1）对陈述性语句赋0分，已有研究表示陈述性语句不属于问题，将“是否为问题”作为编码的首要条件，如回答是陈述性语句，一开始就不进入下一步具体评分[25]；（2）对具有扩展性的数学问题赋4分，蔡金法认为扩展性是问题提出表现重要的评价指标[26]；（3）将具有创新性的问题赋5分，创新性是问题提出的重要因素，也是评价问题提出表现的重要指标[27]．最终确定问题提出表现评估框架如表5所示．

2.4.2 测试任务示例

确定整体评价标准后，结合每题具体情境进行微调形成详细评价标准，下面以礼物情境为例展示评分细则如表6．

2.5 编码信度

在每个班级各抽取20%的测试卷，两位评分者独立编码检验信度，两者编码结果一致性为92%，信度良好．

表3 “平均数”问题提出任务分布结构

表4 刘启蒙和蔡金法的问题提出能力评价框架

表5 问题提出表现评价框架

表6 礼物情境问题提出表现评价框架

3 研究结果

3.1 小学生批判性思维倾向现状

此量表有13道反向计分题，在数据处理时将其转化后取算术平均值来表明小学生批判性思维倾向现状；每个维度分值区间定为1～5，根据高利红的研究对批判性思维倾向水平划分等级如下[16]：大于等于1分且小于2分为低水平组，大于等于2分且小于3分为中低水平组，大于等于3分且小于4分为中高水平组，大于等于4分且小于5分为高水平组．

3.1.1 小学生批判性思维倾向总体分析

小学生批判性思维倾向总体情况如表7．小学生批判性思维倾向整体（=4.05）与高利红的研究结果（=4.09）相近，大部分小学生在中高水平及以上，极少处于中低水平．

表7 小学生批判性思维倾向总体各水平人数分布情况

小学生批判性思维倾向分析结果如表8所示．7个子维度均值由高到低分别是：开放性、求知欲、成熟度、分析性、自信心、求真性、系统性，均处于中高水平及以上．其中开放性、求知欲表现较突出，98%小学生具有中高水平及以上的开放性，表明大部分小学生对别人的观点持尊重包容的态度；超过80%的小学生不管是在学习新的数学知识，还是遇到新的数学问题，或是解题错误时，更倾向于在学会的同时探究其深层次知识与内涵，拥有良好的求知欲．系统性、求真性均值远低于其它子维度，仅有34%的小学生系统性处于高水平，其中只有23%的小学生认为“解数学题就是直接套用公式”是错误的，表明小学生在有组织、有目标地处理数学问题方面还需大力提升；求真性的3个子题项均分都在3.50左右，表明权威、从众心理及情感因素易影响小学生对真理的判断．教育者需关注小学生求真性和系统性的发展．

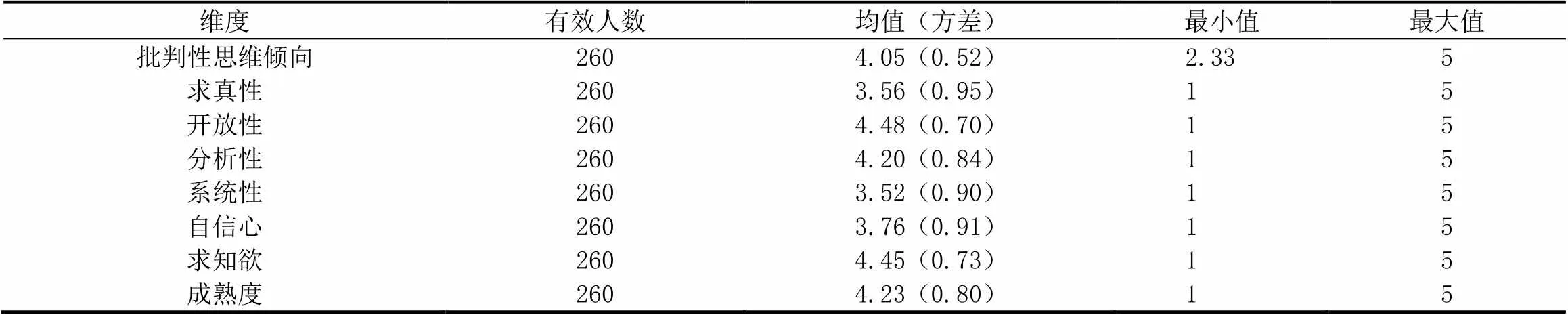
表8 小学生批判性思维倾向各维度描述性分析

3.1.2 城乡小学生批判性思维倾向差异分析

不同地区学生批判性思维倾向表现见表9．城市小学生均值（=4.12）高于农村（=3.95），有统计意义上的显著差异（=2.695，<0.05），表明城市小学生批判性思维倾向强于农村小学生．从各子维度看，城乡小学生求真性、开放性、系统性、成熟度无显著差异，表明不管是城市学习环境还是农村学习环境，小学生都具有良好的开放性和分析性．

表9 小学生批判性思维倾向总体及各维度城乡差异分析

注:**<0.05

结果表明城乡小学生在分析性、自信心、求知欲3个子维度上具有显著性差异．其中自信心差异性最显著（=4.843，<0.05），63%城市小学生自信心处于高水平，但仅有31%的农村小学生自信心处于高水平，大部分城市小学生（68%）对自己拥有的数学思维能力有信心，而仅有不超过一半的农村小学生（41%）相信自己拥有好的数学思维；其次分析性（=2.517，<0.05）和求知欲（=2.217，<0.05）城乡差异性显著，尽管表现都处于高水平，但61%城市小学生在数学学习讨论中，会需要有正当的理由才反对同学的观点，而仅有28%农村小学生认同反对他人观点需要正当理由．城市小学生的求知欲更强，对教师或同学提出的新数学观点有浓厚的兴趣，并热衷于探究其缘由．

3.2 小学生问题提出表现现状

问题提出测试卷由4个问题情境任务构成，需提出12个问题，每个问题分值区间为0～5分，整体分值为0～60分．

3.2.1 小学生问题提出表现整体分析

小学生问题提出表现整体均值为30.50，见表10，表明小学生具有一定的问题提出表现．其中68%的问题是合理可解的数学问题；其中48%的问题是3分问题，即非扩展性数学问题，这类问题符合基本条件，合理且可解，但此类问题的题干条件完全来自情境中已有信息，学生并未改变或增加合理信息；剩下20%的是扩展性问题，表明小学生可以提出扩展性数学问题，甚至个别小学生还可以提出不常见、具有创新性的数学问题，体现出良好的数学思维和创造潜能．

但是，仍有部分小学生（32%）提出不完整的问句、陈述性语句、无关的问题、非数学问题以及不可解数学问题等不合格问题．其中0分问题占15%，示例如下：（1）空白，（2）重复的问题，（3）非完整的问句，例如“7个同学给老师买礼物”是一个陈述性语句，不是问题；（4）与情境无关，例如“卖了10个玩具，爸爸给我了2个，给弟弟多少个？”与幼崽情境中所给出的信息条件完全无关．1分问题占6%，示例如下：（1）相关的非数学问题，例如“老师教什么科目”，（2）重述情境信息的问题，例如“淘气的10个考试成绩的平均值是多少？”2分问题占11%，是不可解的数学问题，学生提出的这类问题与情境有关，是数学问题，没有重述情境信息，但不可解．造成不可解的原因有两点：（1）指意不明，例如，在分数情境中提出“淘气不低不高的分是多少？”此问题中“不高不低”的明确定义范围未给出，从而不可解；（2）缺少条件，例如在礼物情境中提出“平均每人能找回多少元？”此数学问题缺少关键条件，从而不可解．

表10 小学生问题提出表现分析

3.2.2 城乡小学生问题提出表现差异分析

对城乡问题提出表现分析比较发现，城市小学生均值（=31.14）高于农村小学生均值（=29.40）．农村不合格问题（3分以下问题）占比（32%）高于城市不合格问题占比（30%），其中农村小学生0分问题（16%）和1分问题（8%）占比均高于城市小学生（0分问题占比14%，1分问题占比4%），城市小学生2分问题（12%）占比高于农村小学生（8%）；城市小学生合格问题（70%）占比高于农村小学生（68%），从图1可知城市小学生4分问题（21%）和5分问题（2%）均高于农村小学生（4分问题为16%，5分问题为1%），由此表明城市小学生能提出更多的扩展性问题和创新性问题，在这方面表现优于农村小学生．

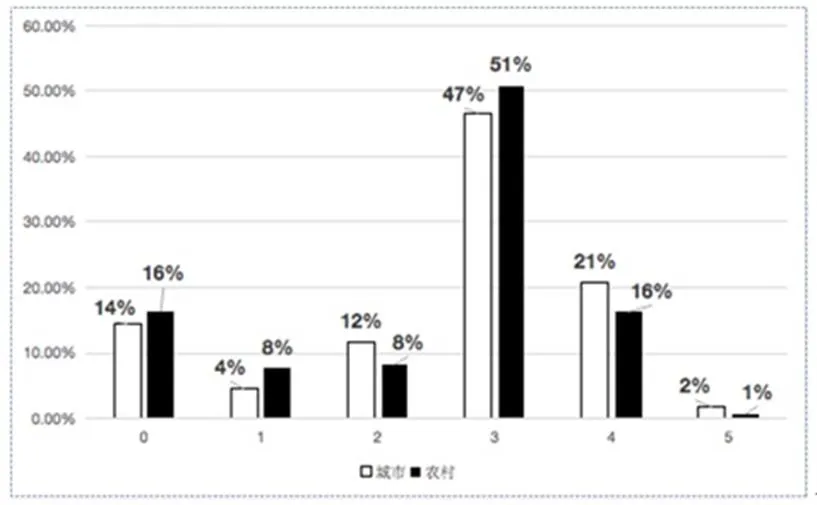
图1 城乡小学生问题提出表现分布

3.3 批判性思维倾向与问题提出表现的相关性

相关性分析结果如表11所示．统计分析证明小学生整体问题提出表现与批判性思维倾向呈中度正相关（=0.422，<0.01），与批判性思维倾向各子维度呈弱正相关．因此，批判性思维倾向越强的小学生问题提出表现越好，可以提出正确且具有扩展性及创新性的数学问题；而问题提出表现越好的小学生批判性思维倾向也越强．

批判性思维倾向子维度中分析性和求知欲与问题提出表现的相关性稍强．分析性越强的小学生，在数学学习与讨论中，更倾向于深入的探究分析，以找出理由来支撑自己的观点；求知欲越强的小学生，越热衷于探究知识背后深层次的意义，不断尝试学习和理解数学；这些对数学抱有浓厚求知欲和强烈分析性的小学生在问题提出表现方面也稍强，倾向于提出更加合理、更具有扩展性及创新性、有价值的数学问题．

在对问题提出表现前25%与后25%的学生进行检验，结果如表12．从检验结果不难看出城乡小学生批判性思维倾向差异性均显著，表明问题提出能力越好的学生其批判性思维倾向越好，但是通过对子维度分析，可发现城市小学生在求真性表现上不具有差异性，其余6个子维度都是显著差异性，表明对于城市小学生，问题提出表现越好，具有越好的开放性、系统性、成熟度，尤其是对自己更有信心，对知识更具有渴望，对问题分析更具有逻辑性．而农村小学生不管问题提出表现高还是低，自信心和求知欲不具有差异性，结合前面结论表明农村小学生并不会因为具有良好的问题提出表现而对自己更有信心．

表11 问题提出表现与批判性思维倾向及其各维度的相关系数

注:*<0.05，**<0.01

表12 问题提出表现水平高低组的批判性思维倾向及其各维度的差异性分析

注:*<0.05，**<0.01

4 结论与建议

（1）问题提出表现与批判性思维倾向具有正相关性，两者相辅相成促进创新教育发展．

以往研究主要在独立研究问题提出或批判性思维的过程性数据中发现问题提出需要批判性思维的参与，该研究在前人基础上，通过统计分析直接证明问题提出表现与批判性思维倾向具有正相关性，即批判性思维倾向越好的小学生，更能提出有价值的数学问题，而越能提出扩展性和创新性问题的学生有着更强的批判性思维倾向，用科学有效的方法证明了已有研究的假设．

问题提出课堂相比于传统课堂有一个更加开放包容的学习环境，可以充分发挥学生的自主力，且提出和分析问题是发展批判性思维的起点，由此可在课堂中设置多样化的问题情境，鼓励小学生从不同的视角出发提出问题，以此促进小学生批判性思维倾向的养成，形成反思质疑的良好习惯；引导学生在学习数学的过程中以问题作为着力点，进行分析评估，以提高学生的分析性和成熟度；通过适当设置开放性的问题和问题提出作业引发学生思考，激发学生批判性思维的发展．问题提出活动需要批判性思维的参与，批判性思维倾向的增强可促进问题意识的产生，而问题提出是问题意识在逻辑和认知经验的催化下形成问题的过程，问题意识是问题提出的起点[9]；再者，批判性思维倾向增强，其分析性、系统性及成熟度大大提升，学生的逻辑能力、分析能力及信息整合能力有所提升，从而提出更有价值的问题．综上，要加强批判性思维与问题提出的结合，两者相辅相成，促进学生创新发展．

（2）加强小学生批判性思维倾向系统性、求真性的提升，重视农村小学生的自信心建立．

整体分析发现部分小学生有错误的数学观，数学学习仅限于知识的程序性理解，只知其然，不知其所以然．其次，小学生在数学学习时易受到权威的影响，实事求是的科学精神还需加强，系统性和求真性亟待提升．值得注意的是，城市小学生批判性思维倾向整体表现强于农村小学生，其中数学学习自信心差异明显，城市小学生远远强于农村小学生．

针对这些现状，社会、学校、家庭应构建开放包容的生活环境和课堂环境以促进学生批判性思维的发展．其中学生系统性的提升，则需要帮助学生获得厘清思路的能力，组织信息解决问题的能力．因此，要重视学生思维习惯的培养，可利用思维图示、问题提出教学法等教学策略，帮助学生整理信息，厘清逻辑，引导学生在学习过程中多角度思考问题，学会层层深入分析和评估[28-30]，教师通过提出问题指引学生思考的方向，教学应“淡化形式，注重实质”，过分注重结论和操作步骤虽能应付考试和习题，会忽视对学生概念性理解的培养，扼杀学生批判性思维的发展，导致学生失去对数学本质的理解[31]．另一方面发展学生探求信息、辨别信息、评估信息的能力，培育求真精神，提升求真性．

城乡小学生自信心差异显著是因为拥有更多前沿数学教育理念的城市教师更懂得如何树立孩子的自信心，而较多农村小学生的家长缺乏对孩子心理健康的重视[32]．这些问题提醒教育者应多关注农村小学教育发展，加强小学生数学自信心的树立，采用正确的评估方式、引导学生正确归因并及时指导学生改进学习方法[33]．

（3）小学生提出问题扩展性和创新性较弱，问题提出融入一线教学亟待开展．

研究结果表明大部分小学生可以提出正确且合理的数学问题，但是扩展性和创新性亟待提升．对不合格问题进行具体分析不难发现部分小学生缺乏数学阅读能力、数学言语表达能力以及对数学问题结构的认识和理解等，从而导致提出的问题存在诸多缺陷．

由此需要通过提升小学生多方面数学素养，如数学阅读能力、数学语言能力等来帮助学生提出正确且合理的问题．掌握数学语言是完成问题提出任务的前提，可通过直观输入、材料加工、转化输出等方法[34]帮助小学生通过阅读、思考、倾听和洞察数学语言所表达的外在概念和数学知识，对其正确使用并有效输出，将现实世界数学化[35]．采用互动合作探究、辨别问题结构等方法提升学生对问题结构的认识，减少提出结构不良的问题[36]．再者，已有研究表明学生的数学观会影响学生的数学学习及成果[37]，错误的数学观（如：解数学题就是套公式）会导致学生机械化地解决问题，缺少思维的参与，由此，日常教学中注重学生正确数学观的树立．问题提出作为数学教育研究的热点，在一线教学中的重视程度和运用范围还亟待加强和扩大，在教学中重视学生创新意识和批判意识的培养，激发其创造潜能，转变传统教学方式，重视问题提出教学，以提升学生数学思维的发散性和灵活性，培养小学生的创造力．张莎莎等研究表明问题提出工作坊能有效提升教师问题提出教学能力，重视问题提出教学的前提是加强教师问题提出教学的培养[38]．

[1] GINI-NEWMAN G, CASE R. Creating thinking classrooms: Leading educational change for this century [M]. Thousand Oaks: Corwin Press, 2018: 1-10.

[2] 伯尼·特里林，查尔斯·菲德尔．21世纪技能：为我们所生存的时代而学习[M]．天津：天津社会科学院出版社，2011：4．

[3] 中华人民共和国国务院．全民科学素质行动规划纲要（2021—2035年）[EB/OL]．（2021-06-03）[2022-03- 24]．http://www.gov.cn /zhengce/content/2021-06/25/content_5620813.htm．

[4] 刘智运，胡德海．对教育本质的再认识[J]．北京大学教育评论，2004（4）：102-107．

[5] EINSTEIN A, INFELD L. The evolution of physics [M]. New York: Simon & Schuster, 1938: 83-86.

[6] TORRANCE E P. Torrance tests of creative thinking [M]. Bensenville: Scholastic Testing Service, 1990: 1-5.

[7] 赵纪东．美国国家研究理事会提出未来十年地球科学领域的12个优先科学问题[J]．天然气地球科学，2020，31（6）：864．

[8] 乔尔·卢迪诺，文森特·巴里．号召批判性思维[M]．上海：学林出版社，2018：1．

[9] 张玲，宋乃庆，蔡金法．问题提出：基本蕴涵与教育价值[J]．中国电化教育，2019（12）：31-39．

[10] NARDONE C F. Critical inquiry across the disciplines: Strategies for student-generated problem posing [J]. College Teaching, 2010, 59 (1): 13-22.

[11] ENGLISH L D. The development of fifth-grade children’s problem-posing abilities [J]. Educational Studies in Mathematics, 1997, 34 (3): 183-217.

[12] 顾明远．教育的本质是生命教育[J]．课程·教材·教法，2013，33（9）：85．

[13] 林崇德．21世纪学生发展核心素养研究[M]．北京：北京师范大学出版社，2016：43．

[14] ENNIS R H. Critical thinking and subject specificity: Clarification and needed research [J]. Educational Researcher, 1989, 18 (3): 4-10.

[15] 荣艳红．中小学课堂教学要培养学生的批判性思维能力[J]．教育实践与研究（A），2012（7）：4-6．

[16] 高利红．小学生批判性思维倾向与数学问题解决表现的关系研究[D]．重庆：西南大学，2020：9-10．

[17] 中华人民共和国教育部．义务教育数学课程标准（2022年版）[M]．北京：北京师范大学出版社，2022：5-6．

[18] 徐斌艳．数学核心能力研究[M]．上海：华东师范大学出版社，2019：103-106．

[19] 蔡金法，姚一玲．数学“问题提出”教学的理论基础和实践研究[J]．数学教育学报，2019，28（4）：42-47．

[20] FACIONE N C, FACIONE P A, SANCHEZ C A. Critical thinking disposition as a measure of competent clinical judgment: The development of the California Critical Thinking Disposition Inventory [J]. Journal of Nursing Education, 1994, 33 (8): 345-350.

[21] 裴昌根，范建成．数学批判性思维倾向问卷的编制及其信效度分析[J]．中国考试，2022（3）：44-50．

[22] 姚一玲，徐冉冉，蔡金法．用“问题提出”诊断和评估数学教师的概念性理解[J]．数学教育学报，2019，28（4）：30-36．

[23] 宋乃庆，胡睿，蔡金法．用问题提出和问题解决测试小学生对平均数的理解[J]．数学教育学报，2020，29（3）：1-8．

[24] LIU Q, LIU J, CAI J, et al. The relationship between domain- and task-specificself-efficacy and mathematical problem posing: A large-scale study of eighth-grade students in China [J]. Educational Studies in Mathematics, 2020, 105 (1): 5-10.

[25] SILVER, EDWARD A, CAI J, et al. An analysis of arithmetic problem posing by middle school [J]. Journal for Research in Mathematics Education, 1996, 27 (5): 521-539.

[26] CAI J. Mathematical thinking involved in U.S. and Chinese students’ solving of process-constrained and process-open problems [J]. Mathematical Thinking and Learning, 2000, 2 (4): 309-340.

[27] XIANWEI Y, van HARPEN, PRESMEG N C. An investigation of relationships between students’ mathematical problem-posing abilities and their mathematical content knowledge [J]. Educational Studies in Mathematics, 2013, 83 (1): 117-132.

[28] 黄蔚，曹榕，齐媛，等．人工智能时代批判性思维能力的提升策略——思维图示的应用对小学生批判性思维能力提升的实证研究[J]．中国电化教育，2019（10）：102-108．

[29] 王丹丹．语文教学中PBL培养小学生批判性思维的研究[D]．武汉：华中师范大学，2020：72-73．

[30] 聂胜欣，俞树煜，袁梦霞，等．异步交互学习活动促进批判性思维发展实证研究[J]．现代远距离教育，2016（3）：60-67．

[31] 陈重穆，宋乃庆．淡化形式，注重实质——兼论《九年义务教育全日制初级中学数学教学大纲》[J]．数学教育学报，1993，2（2）：4-9．

[32] 宋乃庆，唐瑜君，郭磊，等．重大公共卫生事件下小学德育现状与思考[J]．中国教育科学（中英文），2021，4（1）：56-64．

[33] 李善良．论数学学习中自信心的形成[J]．数学教育学报，2000，9（3）：45-48．

[34] 陈万华．指向学生核心素养的数学阅读能力提升策略[J]．江苏教育，2023（22）：51-53．

[35] 吴维煊．数学能力与数学方法[M]．镇江：江苏大学出版社，2008：114．

[36] 谷新龙．以互动合作探究教学促进学生数学思维发展[J]．中国教育学刊，2021（3）：104．

[37] GROUWS A D. Handbook of research on mathematics teaching and learning (A project of the National Council of Teachers of Mathematics) [M]. New York: Macmillan, 1992: 575 596.

[38] 张莎莎，宋乃庆，蔡金法．小学数学教师“问题提出”课堂教学行为研究[J]．数学教育学报，2022，31（2）：46-52．

A Study of the Status Quo of and Relationship between Students’ Problem Posing and Their Critical Thinking Disposition in Mathematics

TANG Yu-jun1, SONG Nai-qing2, CAI Jin-fa3

(1. Shuang Liu Middle School, Sichuan Chengdu 610299, China;2. School of Mathematics and Statistic, Southwest University, Chongqing 400715, China;3. The Department of Mathematics, University of Delaware, Delaware Newark 19716, USA)

Critical thinking tendency, as a necessary component of critical thinking ability, urgently demands the attention of educators. Problem posing is an important cognitive activity for students to learn mathematics, and critical thinking tendency and problem posing are inextricably linked to creativity, which is the key to innovative education. This study investigated the critical thinking tendency and problem-posing performance of 260 randomly selected fifth-grade elementary school students based on the Arithmetic Averaging Problem Posing Test for Elementary School Students adapted from previous studies and the Critical Thinking Tendency Scale for Elementary School Students in Mathematics. Seven subdimensions of the students’ critical thinking tendency were evaluated from strong to weak: openness, curiosity, maturity, analyticity, self-confidence, truth-seeking, and systematicity. The students’ overall critical thinking tendency was strong and their problem-posing performance was at a moderate level, with more than half of the answers being reasonable and solvable mathematical problems. However, the extensiveness and innovativeness of the problems warranted further improvement. The overall positive correlation between the students’ critical thinking tendency and problem-posing performance was moderate: The stronger the critical thinking tendency of the primary school students, the better was their problem-posing performance, and the better their problem-posing performance, the stronger was their critical thinking tendency. The findings of this study provide insights into improving the critical thinking and problem-posing abilities of students.

critical thinking disposition; problem posing; elementary school students; correlation

G623.5

A

1004–9894（2023）05–0035–07

唐瑜君，宋乃庆，蔡金法．小学生批判性思维倾向与问题提出表现的现状及相关性研究[J]．数学教育学报，2023，32（5）：35-41．

2023–08–21

全国教育科学“十三五”规划2020年度教育部青年项目——小学生问题提出能力及其关键影响因素的测评工具研究（EHA200404）；西南大学引进人才计划项目（SWU118118）

唐瑜君（1996—），女，四川巴中人，二级教师，主要从事数学教育研究．蔡金法为本文通讯作者．

[责任编校：张楠、陈汉君]