中学数学问题链教学的“道法术器”

冯园园，宿桂花，张定强

中学数学问题链教学的“道法术器”

冯园园，宿桂花，张定强

（西北师范大学 教师教育学院，甘肃 兰州 730070）

数学问题链教学是落实立德树人根本任务的重要途径．从“道 法 术 器”阐释了问题链教学的指导思想、教法学法、技术路线及问题链的基本形式，并从“设计—实施—评价”一体化的角度提出教学建议：不仅需要重视“道与法”的“顶层设计”，遵循“注重基础、培养创新”的指导思想和问题链的设计思路、结构框架，采取讲授式与发现式并重的教学方法引导学生实现“真探究”；而且需要关注“术与器”的“基础建设”，明确问题链整体设计与分解实施的技术路线，重视问题之间的“方法关联”，依据教学内容合理采用不同形式的问题链，并妥善处理问题链“预设”与“生成”之间的关系．

中学数学；问题链；“道 法 术 器”

1 问题提出

问题是数学的心脏，思想是数学的灵魂．无论是中国古代数学名著《九章算术》中收录的246个数学问题，还是近代德国数学家希尔伯特在巴黎国际数学家大会上作演讲时凝练的23个数学问题，都充分说明数学研究永恒不变的核心就是“问题”，它反映了一定历史时期、特定文化背景下数学研究的发展趋势．而在新兴数学问题层出不穷的信息化时代，传统数学问题也并没有走下神坛，反而为新兴问题的探索提供了宝贵的参考价值．各种各样的数学问题交织在一起，为数学教育研究提供了坚实的知识基础和思想载体．为了顺应这一发展趋势，以问题为主线的教学方式成为越来越多一线教师串联知识、揭示思想、丰富智慧的重要手段，数学课堂也因此成为培养学生问题解决能力的主战场，“问题链”教学模式应运而生．该模式通过一系列问题驱动思维、迁移拓广知识，帮助学生将思想方法运用到问题域中，对深化基础教育数学课程改革产生了深远的影响．相关教学实践也促进了“问题链”教学理论的多元化发展，并对教师专业发展提出了新的要求．从《普通高中数学课程标准（2017年版）》到《义务教育数学课程标准（2022年版）》颁布以来，数学课堂教学越来越提倡落实“四基”、培养“四能”、发展“数学核心素养”，标志着中国数学教育的培养目标经历了从“知识立意”到“能力立意”再到“素养立意”的演变[1]．站在新的高度重新梳理数学“问题链”教学中的“道 法 术 器”，更有利于教师全面地认识问题链教学的指导思想、教学方法和技术路线、工具等，并不断推进相关理论与实践的深化发展．

2 “道 法 术 器”的功能定位

问题是师生在课堂教学活动中实现交互的有效载体，如何构建“问题链”？首先需要明确“问题链”的内涵．朱建中[2]认为，问题链的内涵是问题与问题的精心联结与递进；黄光荣[3]从知识结构的角度指出问题链是数学知识结构的表现形式，提出“问题链方法是以问题为主线，以发现问题—解决问题—再发现问题为全过程，以适应客观世界运动变化和数学严谨逻辑思维之需要为目的的数学思维方法”；唐恒钧等[4-6]认为，“问题链”是指在课堂上呈现给学生的有序的主干问题串，不仅关注基础知识与基本技能的掌握，更关注数学知识结构的深度理解、数学基本思想方法与数学基本活动经验的积累，并且提出确立问题链的3大基点：教学目标、学科思维与学生认知．基于上述分析可以认为，为达到教学目的，伴随问题情境出现的围绕同一核心问题的若干环环相扣的问题就可以构成“问题链”，问题链模式具备渐进式、阶梯式、联锁式[7]等特征，多个问题能否构成问题链模式，关键在于问题之间是否具备有序联结．

3 “道 法 术 器”的理路分析

3.1 “道”——价值取向与指导思想

课程、教师及学生关于数学学习的价值观念是影响数学课程与教学改革的重要因素[9]．在进行问题链教学设计之前，首先应明确问题链教学的功能定位、价值取向与指导思想，即回答“问题链教学的功能是什么”的问题．教育的功能之一是要培养在某个方面具有创造力的有用之人[10]，“通过问题学数学”“不同的学生在数学上得到不同的发展”等教学理念的衍生回应了教育的功能诉求[11]，相应地，数学问题链教学从文化实践的角度在一定程度上取得了“以人为本”的教学理念与“只注重解题、忽视数学的结构化”的现实之间的平衡[12]，为学生数学核心素养的培养提供了现实载体．那么，在实际的问题链教学中如何把握该平衡，这就涉及到“数学问题链教学到底应该教给学生什么”的问题．

对数学的不同认识决定了教师不同的问题链教学价值取向．调查发现，中国大陆数学教师通常把数学看成是一个与逻辑有关的、有严谨体系的、关于图形和数量的、精确运算的一门学科．而事实上，数学是一种多样化的、连续不断地、由问题驱动的人类创造性活动，问题链教学的真正价值就在于通过问题模拟数学知识的生成与思维发展的脉络，并达到应用知识解决问题的目的．没有问题就没有创新，数学问题的提出能发展学生的创新能力并且促使学生成为更好的问题解决者[13]．于是，问题链教学既是问题生成式教学，也是问题解决式教学[4]，也就是在动态建构的过程中从知识深入到“方法、思想与能力”，而不能仅仅停留在“概念、理论与命题”的知识表层．下面以“等差数列通项公式”的教学为例进行说明．

案例1 在本节课的教学中，知识层面的教学目标是“让学生明确等差数列的定义，掌握等差数列的通项公式”，素养层面的目标是“在探究的过程中发展观察、归纳、分析、推理的能力，渗透从特殊到一般的思想方法”，而问题链教学模式则以发展能力、提升素养为目标，可以自然而然地以“思想方法”为引导，帮助学生达到“建构知识框架”“掌握思想方法”与“提升数学素养”齐头并进的效果．

问题链教学的指导思想是以“思想方法”为引导建构数学知识框架．一方面，注重思想方法的渗透和创新能力的培养，通过问题间的思维跨度为学生提供探索的可能性[2]．另一方面，不能忽视学生的知识基础，通过为学生提供环环相扣、逐步推进的问题，使学生获得在内容上较为深入的数学，最终使不同学生的数学素养得到不同的提升．

3.2 “法”——设计思路与结构框架

明晰了问题链教学的“道”，就应确定问题链教学的教学方法、设计思路、结构框架．如前所述，问题链教学的价值在于教会学生思考问题的方法，但这并不意味着要让学生思考和科学家一样的问题，而是让学生领悟发明和发现的精神和方法，用主干问题激发学生对更多问题的思考，并对已有经验进行反思，使学生将已有知识经验进行迁移反思[14]，弗赖登塔尔的“再创造”讲的就是这个道理．因此，问题链教学的课堂设计应关注师生交互的过程，把握讲授式与发现式教学法之间的平衡，不仅关注如何设计问题链，更要关注如何通过问题链教学促使学生深度理解知识、发展能力．

在问题链设计思路方面，“青浦经验”的理论与实践启示数学教学应当实行新问题和旧知识之间的整合，循序渐进，把握知识之间的“潜在距离”，以适合学生的需要[15]．因此，问题之间应具有一定的层次结构、逻辑关系和先后顺序，问题要适切于学生的思维水平，并且具有一定的思维跨度，留给学生独立思考的空间，在解决问题的过程中体现学生的思维脉络．在教学实施中通过讲授式与发现式并重的教学方法，引导学生采取观察、试验、类比、归纳和猜想的学习方法，逐步发现问题、提出问题、分析问题、解决问题，揭示知识的形成、发展过程，使学生建立概念间丰富的网络结构，激发探究意识，培养探究能力[2，5]．

问题与问题之间的主次关系形成了主问题链和子问题链的纽带．因此，教师设计的问题链在宏观框架上，应围绕一个核心问题设置起点问题与若干中间问题（主问题），并依据问题间的主次关系设置主问题链与子问题链（具体设计思路与结构框架如图1所示）．起点问题是问题链教学的起始，从具体情境出发，实现新问题和原有知识之间的整合，循序渐进；主问题链的功能在于体现知识的结构，子问题链在主问题之下，其功能是将学生的思维引入深处，使理解更深刻、具体．

图5表示在不同业务量情况下，采用传统二进制退避BEB算法和DOB算法的系统平均接入时延.由图5可知，在低业务量情况下，由于BEB算法自身的初始碰撞窗口已经固定，在低业务量情况下也会产生退避时延，因此其接入时延较长.DOB算法会根据信道竞争情况，自动调整碰撞窗口值大小，从而减少了不必要的退避时延，降低了系统平均接入时延.另外，当网络节点数N=6时，DOB算法比BEB算法平均接入时延降低了10s.而随着网络节点数量的增加，BEB算法的系统平均接入时延迅速增加，而DOB算法的平均接入时延仍然较低，接入时延参数性能改善明显.

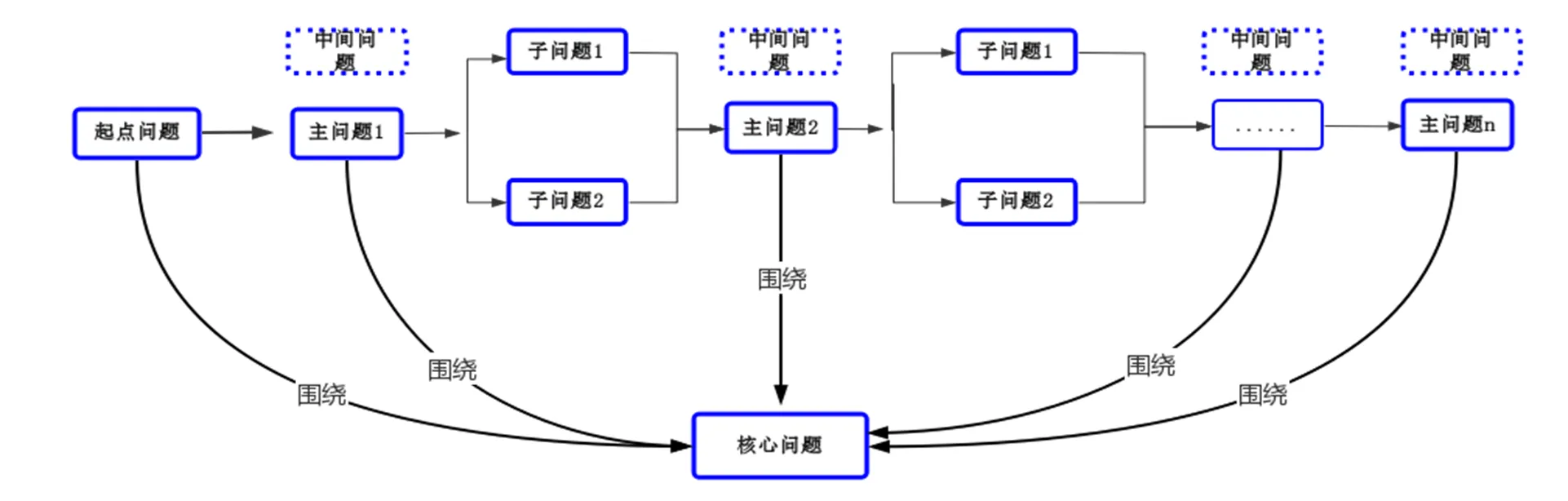
图1 数学问题链的设计思路与结构框架

案例2 在函数的基本性质的学习过程中，节起始部分根据函数图象提出的“你能说说它们分别反映了相应函数的哪些性质吗？”是本节的起点问题，“定义域、值域、单调性、奇偶性”是4个主问题，构成主问题链，也即中间问题，这些问题均指向本节课的核心问题（函数的基本性质）．其中，每个知识点又包括若干个子问题，而每一个单独的知识点也可以构成一个问题链，相应地派生出若干子问题链．随之，子问题链中的核心问题、起点问题与中间问题也需重新确定．因此，主问题链与子问题链涵盖的数学知识内容多少是相对的．

3.3 “术”——技术路线与处理手段

问题链的结构框架，是问题链教学过程中主要教学思路的体现，它是对教学思路的进一步教学化设计．因此，接下来应该关注的问题就是处理问题链的技术路线，即如何建构主问题链？如何通过子问题链完成主问题链教学．

首先，主问题链是统整单元、课时或某一教学环节的核心问题链，具有较大的思考空间，因此主问题链的建构必须反映某一教学单元的整体目标．为此，主问题链的设计应持以整体思维观，在研读课标、分析教材、把握学情及确定教学目标的基础上进行．而学生在解决核心问题的过程中，往往需要通过子问题链引发深度思考，来降低问题理解难度，最终解决核心问题[16]．教师作为基础教育改革发展中最重要的有生力量，设计问题链的能力与问题教学的经验是进行问题链教学的关键[17]，而将主问题链逐级分解为子问题链则是问题链教学的必要手段．

案例3 在运用基本不等式求最值的课时教学设计中，教师首先应确定本节课的教学目标是“学生能够正确运用基本不等式求最值”．其中，基本不等式运用的条件“一正、二定、三相等”是重点，因此为何要及如何满足“一正、二定、三相等”则是问题的核心．于是，主问题链则由分别设计的“一不正”“二不定”（基于学情暂不考虑“三不等”情形，但可以告知学生“三不等”与对勾函数的联系）的子问题构成；而对于“二不定”的问题情境，又会出现“积不定”、“和不定”或分式形式的问题．于是，为了逐个击破这些子问题，子问题链可以被相应地确定下来（图2）．通过探讨“一不正”“二不定”的两种情况均无法使基本不等式成立，从而确定基本不等式的条件．利用反向推理的方法，降低推理难度，并将分类讨论思想与反证法等思想方法贯穿其中．

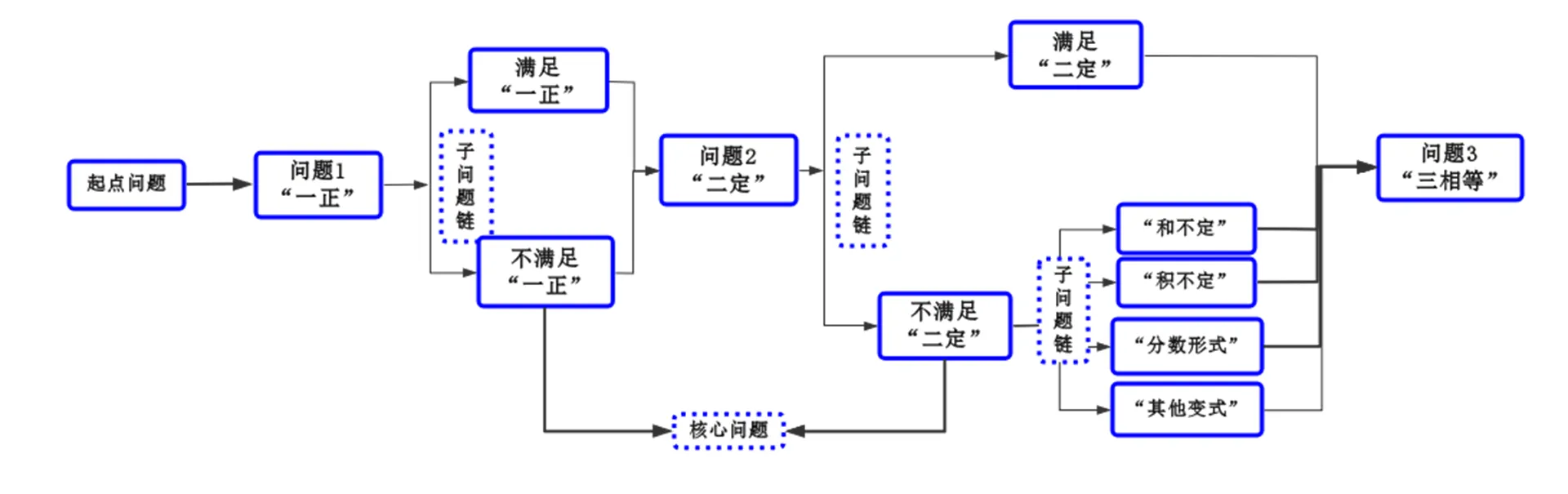
图2 “利用‘基本不等式’求最值”课时问题链示例

其次，在问题链教学过程，应通过理性重构来体现问题间的知识、方法与思考视角关联，才能反向促进问题链整体功能的实现，使课堂问题解决更具整体性．唐恒钧[4]通过调查研究发现新手教师的问题链设计体现知识关联，强调知识层层递进；而专家型教师的问题链设计体现方法关联，强调先粗后细、前铺后琢．依据研究结论，该学者倡导“方法关联”的问题链设计与处理手段，让学生体验、获得数学探究的基本视角与通法，同时倡导问题链教学的单元设计思路，即将具有相同研究视角或共同研究方法的问题作为一个单元进行整体实施．例如，在人教版《普通高中教科书·数学》中，正余弦定理内容划归为“平面向量知识的应用”模块，就是利用“方法关联”建构知识体系的具体表现．通过第一个主题的学习提炼并获得基本的研究视角与方法，并在后续主题中以问题解决的形式加以应用．

最后，问题链是教师课外预设的，但在真实的课堂教学活动中，师生的交互性使课堂“生成”的问题链并不一定与“预设”的相吻合．因此，问题链的课堂教学实践并不是、也绝不能是教师在课堂上提出一个个预先设置好的问题，而应根据师生互动的实际情况灵活调整问题链，使学生在一些重要的数学思想方法的引领下拓展、延伸相应的问题[9]，实现深度学习．

3.4 “器”——基本形式与教学载体

在明确设计思路后，就需要利用动态课程与教学资源，建构基于问题情境的具体问题链，即“器”主要回答“教师在课堂教学中为学生呈现怎么样的问题链”的问题，也即问题链的基本形式，这取决于核心问题的特征与难度．问题是引导探索的，核心问题的解决必须从起点问题出发，通过解决一连串中间问题（问题链）而实现，这就要求教师设计的问题链应具有启发性、层次性和深刻性，反过来，对问题进行推广、引申、综合、深化等操作后，通过中间问题的过渡作用进而可以实现核心问题的探索．这一系列操作体现在问题链教学设计当中，就是教师对不同基本形式的问题链的寻找与建构过程．对此，有学者提出，问题链的基本形式可以大致分为推广（收缩）链、引申链、综合链与深化链4类（表1）．唐恒钧[12]也从一般化、特殊化、类比、逆向等4种基本思维出发，相应地提出推广链、特殊链、类比链与逆向链这4类问题链（表2）．

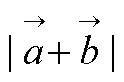
该案例所呈现的问题链，围绕“平面向量的运算法则”这个核心问题，以问题①为起点问题，②③④⑤为中间问题（也即主问题），通过数的加法性质与力的合成，类比向量的加法性质，在得到向量平行四边形法则的基础上，引导思考三角形法则的性质，最后以问题⑤逐步引导学生对向量三角形法则的理解走向深化，是以深化链为基本形式的问题链．

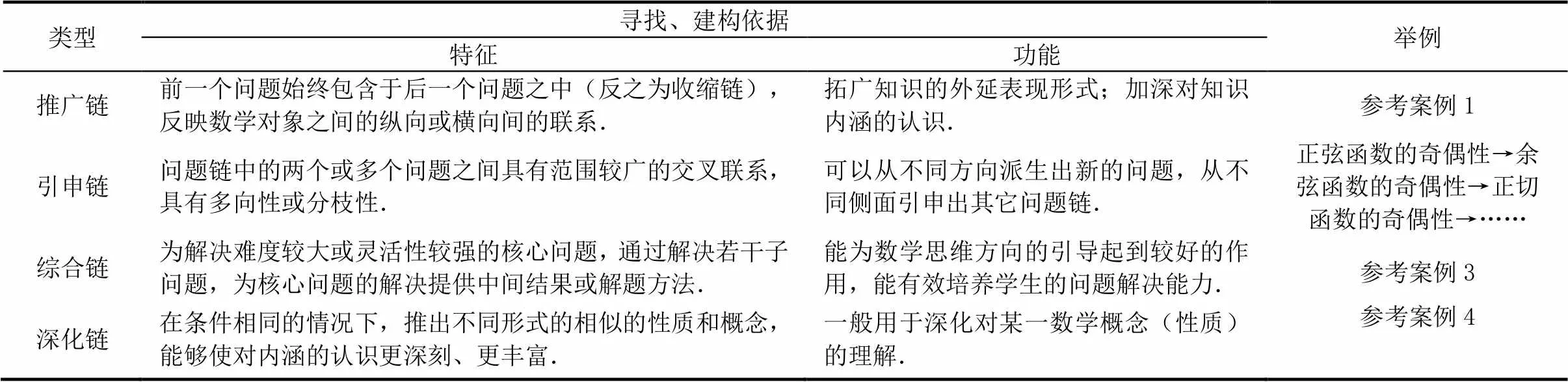
表1 数学问题链的基本形式——案例1

表2 数学问题链的基本形式——案例2

案例5 再以“补集思想”进行详细说明．如下题目[18]：小明家中有甲、乙、丙3个闹钟，他每天准时起床必须靠闹钟叫醒自己．假设任一闹钟响就能起床，甲闹钟准时响的概率是0.8，乙闹钟准时响的概率是0.9，丙闹钟准时响的概率是0.75，求小明能准时起床的概率．

若依据原问题设置“求小明不能准时起床的概率”的逆向链，进而由“甲闹钟不能按时响的概率”“乙闹钟不能按时响的概率”“丙闹钟不能按时响的概率”的问题链，引申出“甲、乙、丙3个闹钟都不能按时响的概率”的问题，就可以大大降低原问题的理解难度．

此外，不同形式问题链的建构还可以从其它不同角度出发，如依据数学知识（概念、命题、定理等）、数学思想方法、数学规律等寻找与建构概念链、命题链、方法链等问题链；依据数学学科核心素养、十大核心词等寻找与建构运算链、推理链等问题链．凡此种种，所有基本形式均体现了以问题为主线，以“提出问题—解决问题—再发现问题”为全过程的、兼具收敛性和发散性的数学思维方法，能够为教师问题链的寻找与建构提供基本参考依据[3]．

4 基于数学问题链教学优化的教学建议

基于数学问题链的教学设计与实施是一项系统工程，要遵其“道”：注重基础与培养创新相结合；循其“法”：讲授式与发现式相结合；明其“术”：整体设计与分解实施相结合；用其“器”：课前预设与实际生成相结合．不仅关注问题链的“设计”，也要关注问题链的“实施”与“评价”，坚持“教、学、评”一体化，进而构建完善的问题链教学“设计—实施—评价”体系，具体流程如图3所示．

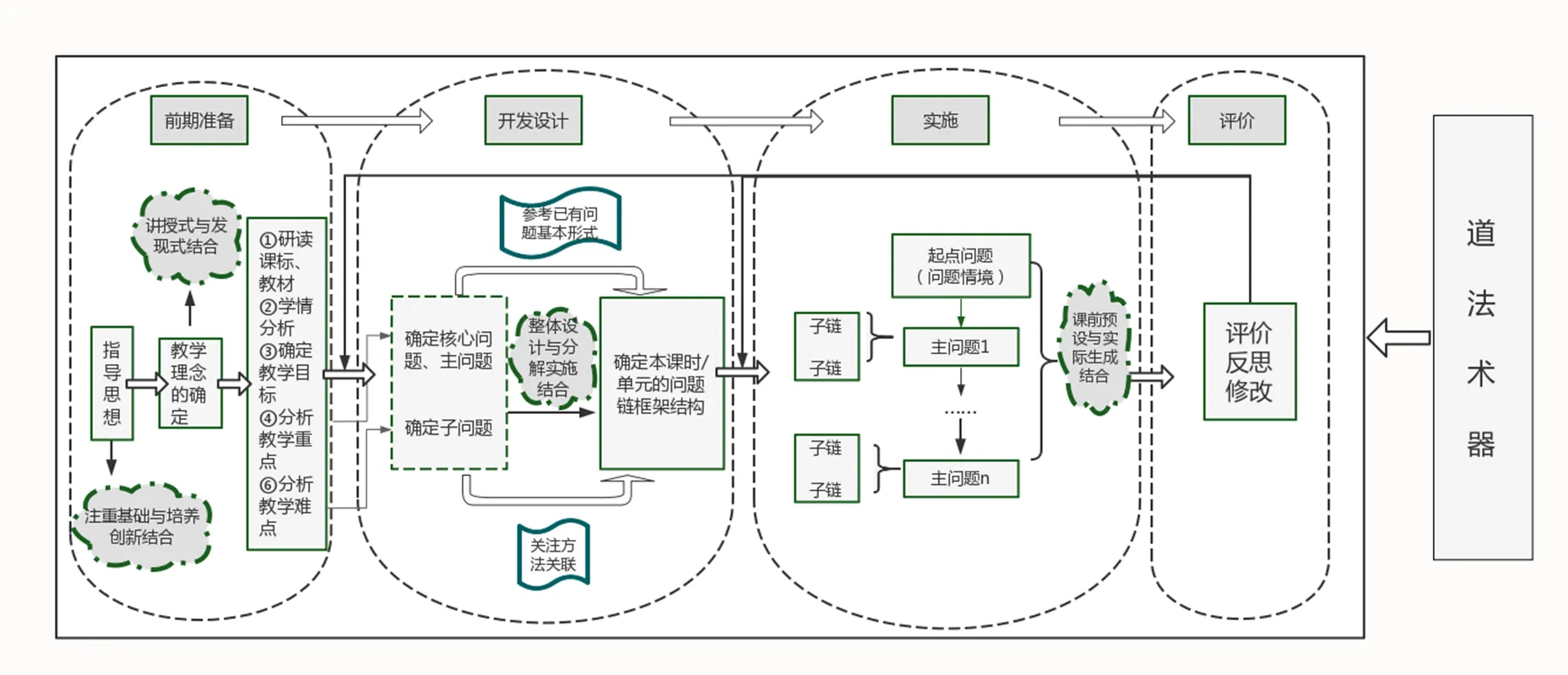
图3 数学问题链教学“设计—实施—评价”体系

4.1 顶层设计——道法一体

基于“问题链”的教学应充分发挥问题驱动培养学生问题解决能力的功能，体现“问题解决式”的教育价值取向，遵循“注重基础、培养创新”的指导思想；明确主问题链与子问题链的设计思路与结构框架，并以讲授式与发现式并重的教学方法引导学生实现真正的自主探究，坚持实现“道”与“法”的辩证统一．

具体而言，在教学设计方面，问题链的创设必须把握好注重基础与培养创新的平衡点．衡量问题链教学价值的标尺并不在于其囊括了多少精深、生僻的问题，而贵在其能否让学生体会思考问题的方法与视角、并不断建构新知识[6]．在实施方面，不仅关注教师的引导，还应在师生交互的过程中，引导学生进行独立探索，这是问题链教学中非常重要的学习行为[4]．因此，在问题链教学的推进过程中，学生不仅是回答问题、解决问题，还应发现、提出问题，教师则应给学生“冷静思考的时间”和“充分表达的机会”．在评价方面，教师应关注自身设计的问题链是否体现了“问题驱动式”与“问题解决式”的指导思想和教学理念，是否能够有效引导学生通过问题建构数学知识框架并持续探索；关注学生是否能够真正通过观察、试验、猜想等学习行为进行问题链的探索．

4.2 基础建设——术器合一

基于“问题链”的教学不仅需要重视“顶层设计”，还应关注“基础建设”．在问题链的寻找与建构过程中应依据教学内容合理采用多种不同形式的问题链，明确问题链整体设计与分解实施的技术路线，重视问题之间的方法关联，在问题链形式的选取上坚持课前预设与实际生成相结合，达到术器合一．

具体而言，在教学设计方面，教师应当积极开发教学资源，扩大问题搜索范围，并依据教学内容筛选问题类型，依据知识内容的特征确定问题链的基本形式．在技术路线上应从宏观入手，整体设计主问题链，逐步过渡到微观，将主问题链分解到各个课时去完成，引导学生的思维不断深化发展．在实施方面，教师应当注重不同问题之间的“方法关联”，兼顾“知识关联”，兼顾学生思想方法的掌握与知识框架的持续建构．倘若教师设计的问题链忽视问题间的关联，就会使问题链教学沦为机械式的问题堆积与题海训练，从而不利于学生知识框架的建构与问题解决能力的培养．同时，教师在实施过程还应把握先慢后快、先松后紧的教学节奏，使得学生建构知识、探索未知的空间也先小后大[4]，因此，教师不能满足于预设好的、具有逻辑关联的问题链形式，更不能“郑人买履”或生搬硬套，而有必要依据实施中的具体情况灵活调整预设的问题链，抓住师生互动过程中“实际生成”的每一个有价值的问题．在评价方面，教师应思考自身是否能够依据教学内容为学生呈现合适的问题链形式，关注自身是否能够在整体观的指导下设计与实施问题链教学，是否能够有效处理问题链的预设与生成之间的关系，采取的知识关联或方法关联是否与本节课的知识内容相适应等．

5 结语

从“道 法 术 器”的角度梳理数学问题链教学，实则也是对现代数学教育哲学视角下问题链教学的“价值论”“目的论”及“方法论”的初步探索，这对数学问题链教学的理论探索和实践操作均具有现实意义．后续研究应继续侧重于问题链教学的实践，开展更为丰富的案例分析，如探析单元、大概念、深度学习等视域下的问题链（范畴、难易、方法、思维等）教学设计、实施、评价的理路等．

[1] 王尚志，胡凤娟．高中数学课程标准“修订思路”“组织”及“过程”[J]．数学教育学报，2018，27（1）：11-13．

[2] 朱建中．如何巧置“问题链”发展学生思维[J]．教育教学论坛，2010（36）：48．

[3] 黄光荣．问题链方法与数学思维[J]．数学教育学报，2003，12（2）：35-37．

[4] 唐恒钧， TAN H，徐元根，等．基于问题链的中学数学有效教学研究——一项课例研究的启示[J]．数学教育学报，2018，27（3）：30-34，44．

[5] 唐恒钧，张维忠，陈碧芬．基于深度理解的问题链教学[J]．教育发展研究，2020，40（4）：53-57.

[6] 唐恒钧，张维忠．数学问题链教学的内涵与特征[J]．教育研究与评论（中学教育教学），2021（1）：8-12．

[7] PENG H M. Coupling study on the problem chain teaching mode and moral education construction in primary and secondary schools [J]. Journal of Literature and Art Studies, 2020, 10 (8): 738-742.

[8] 张清学，孙姚同．“互联网+”背景下成人高教在线课程开发的道、法、术、器[J]．中国成人教育，2015（23）：158-160．

[9] 任伟芳．问题链数学教学研究的缘起、实践与愿景——唐恒钧教授访谈录[J]．中学数学，2020（3）：87-89，91．

[10] 曹广福，刘丹．课题式教学法探析[J]．数学教育学报，2020，29（3）：32-36．

[11] 张定强，冯园园，马卖艳．论高中数学教育育人方式变革[J]．数学教学研究，2021（2）：2-5，21．

[12] 唐恒钧，张维忠．问题链教学的理论与实践[M]．上海：华东师范大学出版社，2021：82-92．

[13] 陈婷，李兰，蔡金法．中国小学数学“问题提出”教学的研究与实践——基于《小学数学教师》和《小学教学》（数学版）中“问题提出”文章的分析[J]．数学教育学报，2021，30（1）：19．

[14] 葛丽婷，施梦媛，于国文．基于UbD理论的单元教学设计——以平面解析几何为例[J]．数学教育学报，2020，29（5）：25-31．

[15] 刘影，程晓亮．数学教学论[M]．北京：北京大学出版社，2009：50-70．

[16] 杨丽芳．整体观视角下的课堂教学问题链设计——以人教版小学数学“解决问题”新授课的教学为例[J]．教育与教学研究，2018（3）：59-63，128．

[17] 宋乃庆，张莎莎，陈婷，等．基于“问题提出”的小学数学教师主题式专业发展：理论建构与实践探索[J]．数学教育学报，2021，30（1）：12．

[18] 梁会芳．高中生数学逆向思维的现状调查研究[D]．兰州：西北师范大学，2021：85．

“Dao FA Shu Qi” in Mathematics Problem Chain Teaching

FENG Yuan-yuan, SU Gui-hua, ZHANG Ding-qiang

(College of Teacher Education, Northwest Normal University, Gansu Lanzhou 730070, China)

Mathematics problem chain teaching is an important way to implement the fundamental task of “Building Morality and cultivating people”. This paper explains the guiding ideology, teaching and learning methods, teaching techniques and substantial forms of problem chain teaching from the perspective of “Dao FA Shu Qi”, and puts forward some teaching suggestions from the perspective of the integration of “Design-Implementation-Evaluation”. On the one hand, we should pay attention to the “Top-level design” of ideology and method: follow the guiding ideology of “Laying stress on foundation and cultivating innovation” and the design ideas and structural framework of the problem chains; both of the lecture and discovery method should be adopted to guide the students to achieve the “True inquiry”. On the other hand, we should pay attention to the “Basic construction” of teaching techniques and substantial forms: clarify the technical route for the overall design and decomposition of Problem Chains, and pay attention to the “Method connection” between the problems. In addition, various types of problem chains should be reasonably adopted according to the teaching content, and properly handle the relationship between “preset” and “generation” of the problem chains.

middle school mathematics; problem chain; “Dao FA Shu Qi”

G40–03

A

1004–9894（2023）05–0042–05

冯园园，宿桂花，张定强．中学数学问题链教学的“道 法 术 器”[J]．数学教育学报，2023，32（5）：42-46．

2023–06–21

国家社会科学基金“十三五”规划2018年度教育学西部项目——西北民族地区高中生理科学科核心素养培育路径研究（XHA180288）

冯园园（1997—），男，陕西榆林人，硕士生，主要从事数学教学论研究．张定强为本文通讯作者．

[责任编校：陈隽、张楠]