用“问题提出”诊断和评估数学教师对百分数的概念性理解

孙 枚，李 欠，王 涛，王 欣，蔡金法

用“问题提出”诊断和评估数学教师对百分数的概念性理解

孙 枚1，李 欠2，王 涛3，王 欣4，蔡金法5

（1．天津市河西区教师发展中心，天津 300203；2．天津市河西区平山道小学，天津 300074；3．塔尔萨大学 教育系，俄克拉荷马 塔尔萨 74104；4．天津市河西区上海道小学，天津 300204；5．特拉华大学 数学系，特拉华 纽瓦克 19716）

通过对99名不同背景的教师有关百分数问题提出和问题解决表现的分析，发现绝大部分教师能解答简单的百分数问题．对于复杂的百分数问题，教师的问题解决明显受他们背景的影响．虽然教师的问题提出和问题解决能力存在着高度相关，但是绝大部分教师无论他们的背景以及问题解决能力如何，都能提出难度不同的百分数数学问题，并显示不同层次的百分数概念理解．相较于问题解决，问题提出更能全面地显示教师对百分数概念理解的光谱．对教师所提问题的进一步分析显示，绝大部分教师对百分数的理解还局限于比的概念维度．

问题提出；问题解决；百分数；教学评估；教师培训

近年来，问题提出的重要性越来越受到世界各国的关注和重视[1]．过去30年的研究已经累积了相当多的证据支持问题提出不仅可以促进学生学习，还能培养创新能力[2]．《义务教育数学课程标准（2022年版）》将“发展运用数学知识与方法发现、提出、分析和解决问题的能力”作为核心素养导向的课程目标的一部分[3]，特别强调问题提出教学的重要性，并认为这会直接影响到学生数学素养的培养．而教师作为基础教育改革中重要的有生力量，其“问题提出”能力及“问题提出”的教学经验是培养学生“问题提出”能力的重要前提[4]．然而目前教材中含有的问题提出的教学活动并不多[5]，这导致教师在将“问题提出”教学融入课堂时会面临巨大挑战．因而在教师培训中，更需要为教师提供感受问题提出过程的机会，让他们看到问题提出的优势，以帮助其设计实施有效的问题提出教学．基于这样的需求，研究采用百分数问题来考察教师在问题提出和问题解决中的表现，以期了解不同背景的教师对百分数概念的理解以及他们问题提出和问题解决能力之间的关系．

1 理论基础

为了让学生在学习中顺利理解数学概念，教师自己必须对数学概念有扎实的理解[6]．与此同时，教师还需要把握学生的知识水平和思维状态，这样他们才能更好地在课堂里为学生提供有效的学习机会．过去的研究已经明确指出问题提出对教师了解把握学生数学思维的独特作用．例如，Cai和Hwang指出，问题提出是了解学生数学思维和理解的一扇窗户[7]．Ticha和Hospesova发现教师的问题提出能力与其对数学概念的理解程度存在显著相关性，问题提出既可以作为了解学生和教师对数学概念的理解类型和程度的手段，也可以促进他们对数学概念的理解[8]．

目前，有关用问题提出诊断学生和教师数学概念理解的研究还比较有限．宋乃庆等用问题提出测试了321名五年级学生对平均数概念的理解，发现：学生在平均数任务情境下能够提出较多的合理数学问题，随着要求难度的提升，学生所提数学问题更加新颖和复杂[9]．Yao，Huang和Cai（2021）的研究关注的是职前教师对分数除法的理解，研究发现：虽然几乎所有的职前教师都能做对分数除法的数学问题，但是他们的问题提出却显示他们对分数除法的理解非常局限，这项研究体现出问题提出比问题解决在诊断评估教师的数学理解上存在一定的优势[10]．姚一玲等（2019）用问题提出调查了在职教师对分数除法的理解，发现：在职教师对分数除法意义的概念性理解较为缺乏；职称越高的教师对分数除法概念的理解越好，但是仍然有一半以上的教师对分数除法的概念是程序性理解[11]．总体而言，如何用问题提出来探究教师或学生对重要数学概念的理解这一重要课题尚需要更多的研究投入．

近年来，问题提出与问题解决之间的关系也是学界研究的热点，第14届国际数学教育大会（ICME-14）设置了“问题提出与问题解决”主题研究小组（TSG17），在强调问题解决研究重要性的同时凸显问题提出的教育价值[12]．因此，对于教师问题提出与问题解决的表现以及两者间内在联系的研究，有助于深入考察教师的思维过程及其概念性理解．

众所周知，百分数是小学数学的一个重要概念．《义务教育数学课程标准（2022年版）》中百分数有了新变化，从原来的“数与代数”领域移至“统计与概率”领域，百分数将作为表达统计量的一种形式，凸显其统计意义[3]．在义务教育阶段强调发展学生数据分析观念，强化统计教育，合理进行统计教学成为各国课程改革关注的热点课题[12]．百分数作为重要的统计概念，其内涵十分丰富，Parker和Leinhardt（1995）认为百分数至少有5个方面的含义：数、比、比率、统计量和算子，而教师对这5方面含义的理解会直接影响他们能否有效执教百分数[13]．同时，以往研究表明，教师的数学概念理解在问题提出中扮演极为重要的角色，Isik和Kar（2012）发现教师如果缺乏足够的概念理解会直接有碍于他们的问题提出[14]．然而，有关用问题提出诊断学生和教师的数学概念理解的研究还有待进一步加强，目前并没有研究采用问题提出这一特殊的研究手段来探究教师对百分数这一重要概念的理解．研究旨在通过对如下问题的考察，对现有文献做出独特的贡献：（1）教师在百分数问题提出上的表现；（2）教师在百分数问题解决上的表现；（3）教师在百分数问题提出和问题解决上的表现呈现的关系；（4）教师背景与教师在百分数问题提出和问题解决表现之间的关系．

2 研究方法

2.1 研究对象

调研地区共有小学数学教师七百余名，研究者借助当地的教师研修活动，随机抽取了其中的99名小学数学教师参加此次问卷调查．这99名教师的背景信息如表1所示，研究者分别从职称、教龄、执教百分数的次数进行了统计．

表1 研究对象的背景信息

2.2 调查工具

此次调查共包含3道测试题，分成两张问卷完成，且均为纸笔测试．研究者要求每位参与调查的教师现场完成两份问卷．问卷一包含一道测试题[15]；问卷二包含两道测试题．

【问卷一】

1．根据下面的两个数和百分数的符号，提出4个难度不同的用百分数解决的数学问题．

40 50 %

a．简单问题

b．中等问题

c．偏难问题

d．较难问题

注意：只需要提出数学问题，不用解答．

【问卷二】

1．在星期六售出的雪糕中，有40%是巧克力味．在星期天售出的雪糕中，有50%是巧克力味．于是淘气说，雪糕店在星期天售出的巧克力雪糕比在星期六售出的巧克力雪糕多，因为50%比40%大．淘气说得对吗？请说明理由．

2．张华在2019年初因为工作表现出色，工资上涨8%；2020年初由于受到新冠疫情的影响，工资下降8%．

（1）张华2020年的工资与2018年的工资相比，哪一年的工资多？多多少个百分点？请详细解释你是怎么得到你的答案的．

（2）张华2020年的工资与2018年的工资相比，哪一年的工资少？少多少个百分点？请详细解释你是怎么得到你的答案的．

问卷一是围绕“40、50、%”3个信息，提出4个难度逐渐提升的数学问题，即：简单问题、中等问题、偏难问题、较难问题．问卷二是解决百分数相关问题．因问卷二的第1题涉及问卷一中的“40、50、%”3个信息，为避免问卷二对问卷一产生提示作用，研究者将两份问卷分别下发，即：先下发问卷一，当全体教师完成问卷一后，将问卷一全部收回，再下发问卷二．另外，为保证测试结果的准确性，消除教师对问卷结果影响自身发展的顾虑，调查采取不记名的方式进行．

2.3 数据编码及分析

问卷一是关于百分数“问题提出”的调查．围绕“40、50、%”3个信息提出用百分数解决的数学问题将会覆盖很多内容．因此，对调查结果进行细致编码，图1总结了研究中开发和使用的编码方案．

图1 提出问题数据编码方案总结

首先，将教师们提出的问题分成“情境相关问题”和“情境无关问题”．所谓“情境相关问题”是指：在“40、50、%”3个信息中，使用“%”和至少一个数据（40或50）提出的问题．否则是“情境无关问题”．

接下来，将“情境相关问题”分成“能解答的问题”和“不能解答的问题”．不能解答的问题是指缺乏足够信息，或者提出与给定信息不兼容的问题．如：“已知两瓶盐水的质量，含盐量是40%和50%．求两瓶盐水中盐的质量．”这道题，虽然教师指出“已知两瓶盐水的质量”，但两瓶盐水的质量具体是多少未呈现，由于题目信息的不完整导致问题不能解答．又如：“一班有40人参加兴趣小组，比另一个班多50%．另一个班有多少人参加？”这道题，根据问题列出的算式是40÷(1+50%)，通过计算发现，计算结果不是整数，与“人数”情境不符．因此，类似这样的题目被视为“不能解答的问题”．

将“情境无关问题”分成“一般性描述”和“不含相关信息的问题”．一般性描述是指教师描述了百分数知识的类别（如图2）．不含相关信息的问题是指属于百分数问题，但未使用“40、50”任意一个数据的问题（如图3）．

图2 一般性描述

图3 不含相关信息的问题

最后，又将能解答的数学问题分成“需要运算解决的问题”和“不需要运算解决的问题”．不需要运算解决的问题指涉及百分数的读法、意义、比大小等问题，如：“40%读作什么？”“40%表示什么意思？”这些问题在解决的过程中不需要运算就可以解决．对于需要运算解决的问题按解决问题的步骤进行细分，编码的典型类型及示例见表2．

在按步骤细分的过程中，为了实现最终计算步骤的一致性，制定以下3条原则．一是，采用算术解法计算步骤．如“一杯糖水重50g，糖占40%．再添多少克糖，使糖占50%？”解决此题通常会出现方程和算术的不同解法（如图4），为体现统计的一致性，研究者按照算术解法计算步骤，最终计为5步．二是，采用解决问题的最简方案计算步骤．如“一本书有100页，已经读了其中的40%．再读剩下的50%．还剩多少页没读？”解决这道题通常会有3种方法（如图5）．方法一和方法二列出的都是综合算式，但解题思路不同，方法一是先统一参照标准，再求剩余的页数，需要5步完成；方法二是先求第一次读完剩余页数，再求第二次读完剩余页数，只需4步完成．方法三和方法一解题思路相同，都是先统一参照标准，再求剩余页数，但方法三列出的是分步算式，4步即可完成．综合以上3种方法，依据采用解决问题的最简方案计算步骤，最终计为4步．三是，解决问题“不跳步”．如“有甲、乙两桶油，甲桶油有40千克，如果乙桶倒给甲桶50千克，两桶油就同样多了．原来甲桶油比乙桶油少百分之几？”解答这道题常会出现两种方法（如图6）．方法一，由题目信息“如果乙桶倒给甲桶50千克，两桶油就同样多了”，可以推断出甲、乙两桶油相差的是“50×2”千克，因此在求两桶油的差时，舍去了用甲桶油的重量加上“50×2”，再减甲桶油的重量的过程，即跳过了“加40”和“减40”的步骤，此方法共计3步完成．方法二，则是将求两桶油的差的过程完整表达出来，共计4步完成．因此，基于解决问题“不跳步”的原则，此题最终计为4步．

表2 按步骤编码的类型及典型示例

综上，基于小学阶段四则混合运算原则不超过3步，因此，在实际教学中解决以上的题目也就通常采用综合与分步算式相结合的方法解决问题．

图4 方程和算术解法

图5 3种解题方法

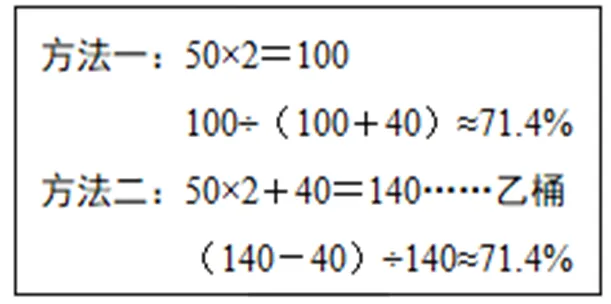
图6 2种解题方法

问卷二是关于解决百分数问题能力的调查．第1题包含两问，第一问是判断题，只有对与错两种结果；第二问是基于第一问判断的结果进行说理，只区分说明的理由合理与不合理．第2题包含两道小题，每道小题均有连续性的3问，总计是6个小问题．两道小题之间有较强的关联性，都是将2020年工资与2018年工资进行比较，然后追问“谁多（少）？多（少）多少个百分点？详细解释你是怎么得到你的答案”．这道题共考查了解决百分数问题的两个知识点．一是比较两年工资的多少，是对被调查者转化单位“1”的能力进行考查．因为要想比较2020年工资与2018年工资，就需借助“2019年上涨了8%”和“2020年下降了8%”这两条信息，将2020年和2018年建立联系，即：设定2018年为“1”，2020年就是1×(1+8%)×(1-8%)=99.36%，1>99.36%，所以2018年多，2020年少．另一个是求谁比谁多（少）几个百分点，这是对被调查者解决“求一个数比另一个数多（少）百分之几”问题的能力考查．研究将第2题的解答分为3类：第一类是完全正确（如图7）；第二类是部分正确，被调查者仅能正确解释2018年和2020年工资谁多谁少的问题，即两道小题的第1问，未能解决多（少）多少个百分点的问题（如图8）；第三类是完全错误（如图9）．

图7 完全正确举例

图8 部分正确举例

最后，确定编码方式后，99份试卷由两位参与研究的教师分别进行编码，两份问卷的编码一致性达到95%以上．

3 研究结果

3.1 教师在问题提出上的表现

3.1.1 教师提出问题的数量

在调查中，99位教师共提出364个问题，教师提出问题的数量是要求提出问题总量（每人4个问题，共计396个问题）的91.9%．全部教师都能至少提出2个问题，77.8%的教师能提出4个问题．说明大部分教师都能按照要求提出4个问题．

表3是教师在问题提出数量上的表现．教师提出的问题中，有88.2%是情境相关问题，11.8%是情境无关问题．在情境相关问题中，有80.2%是需要运算解决的问题，有6.9%是不需要运算解决的问题（即：百分数的读法、意义、比大小等），不可解决的问题仅有1.1%．显然，绝大部分教师提出的问题是需要运算解决的问题．相较于百分数的意义、读法等基本概念性问题，他们更加关注百分数在数量关系层面的问题．在情境无关问题中，有10.4%属于一般性描述，不含相关信息的问题仅有1.4%．这38个一般性描述问题来自13位教师，其中有9人未执教过百分数，而8人都是教龄低于5年的青年教师．由此可见，没有执教百分数的经历会导致教师对百分数概念本身产生困惑，他们往往只能从知识的类别这个角度提出一些问题，如定义、比大小、计算、解决问题等，而不能结合情境提出相应的、有意义的数学问题．

表3 教师提出问题数量的表现

3.1.2 教师提出问题的难度

从问题整体看，“情境相关问题”中“能解答的问题”共有317个，按照问卷一对问题提出的要求和运算步骤进行编码并统计．为了实现对全部能解答的问题进行分析，将不需要运算的问题记作0步，最终形成表4．

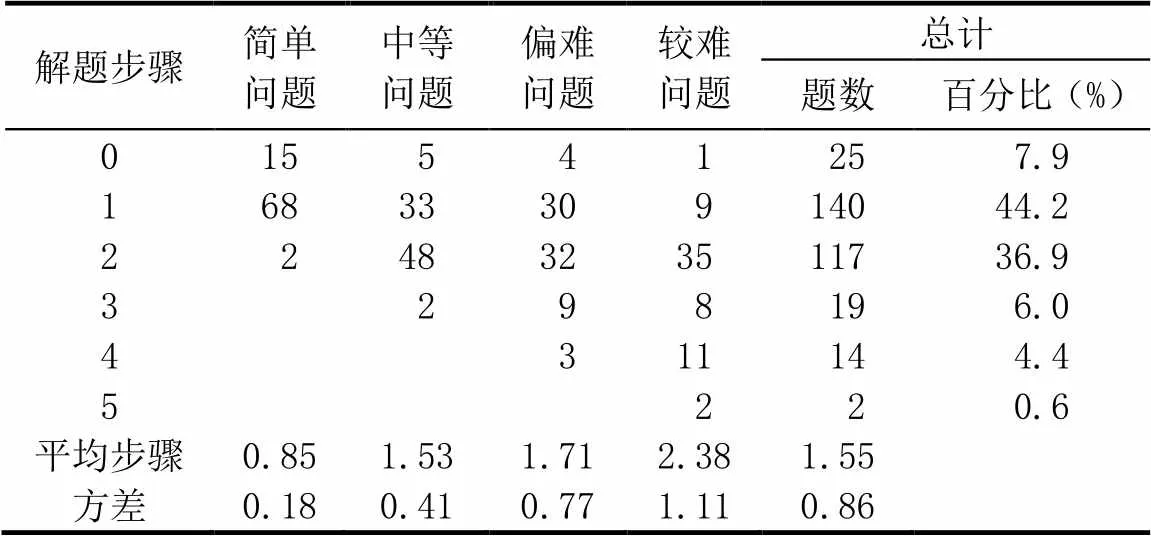
表4 教师提出问题难度的表现

通过表4可以看出，一步运算解决的问题数量最多，几乎是所有问题的一半；其余的问题随着解决问题步骤的增加，数量在逐步减少．由此可以看出，教师在提出问题时有意识地区分问题的难度，努力达到自己心目中的简单、中等、偏难、较难4个梯度．基于此，将教师提出问题的难度与解决问题的步骤进行综合分析，按照问题难度（简单、中等、偏难、较难），依次计算出每一类问题的平均步骤和方差．以简单问题为例，教师提出15个不需要运算解决的问题，68个需要一步运算解决的问题，2个需要两步运算解决的问题，在总共85个问题中，平均每个问题所需的步骤为0.85，即(15×0+68×1+2×2)÷85=0.85．而其它3类问题的平均步骤分别为1.53、1.71、2.38．方差分析检验显示不同难度的问题其平均解题步数存在非常显著的差异，(3, 302)=52.30，<0.001．也就是说难度越大，解题步数越多．由此可以看出，教师在提出4个难度不同的问题时，有意识将解决问题的步骤作为区分问题难度的一个标准．

3.1.3 教师提出问题类型和涉及百分数意义的表现

将“需要运算的问题”从问题类型、百分数的意义和百分数的应用看，主要涉及以下8种类型（如表5），其中91.4%的问题都是围绕百分数的意义和应用展开．排在前三位的是“一个数是另一个数的百分之几”“一个数比另一个数多（少）百分之几”“求一个数的百分之几是多少”，分别为30.9%、24.5%和19.8%．“已知一个数的百分之几是多少，求这个数”和“已知比一个数多（少）百分之几是多少，求这个数”，这两类逆向问题占比较低，分别为5.0%和1.8%．由此可以看出，当教师们主动提出问题时，更偏向提出正向思考的题目，对逆向思考的题目关注较少．

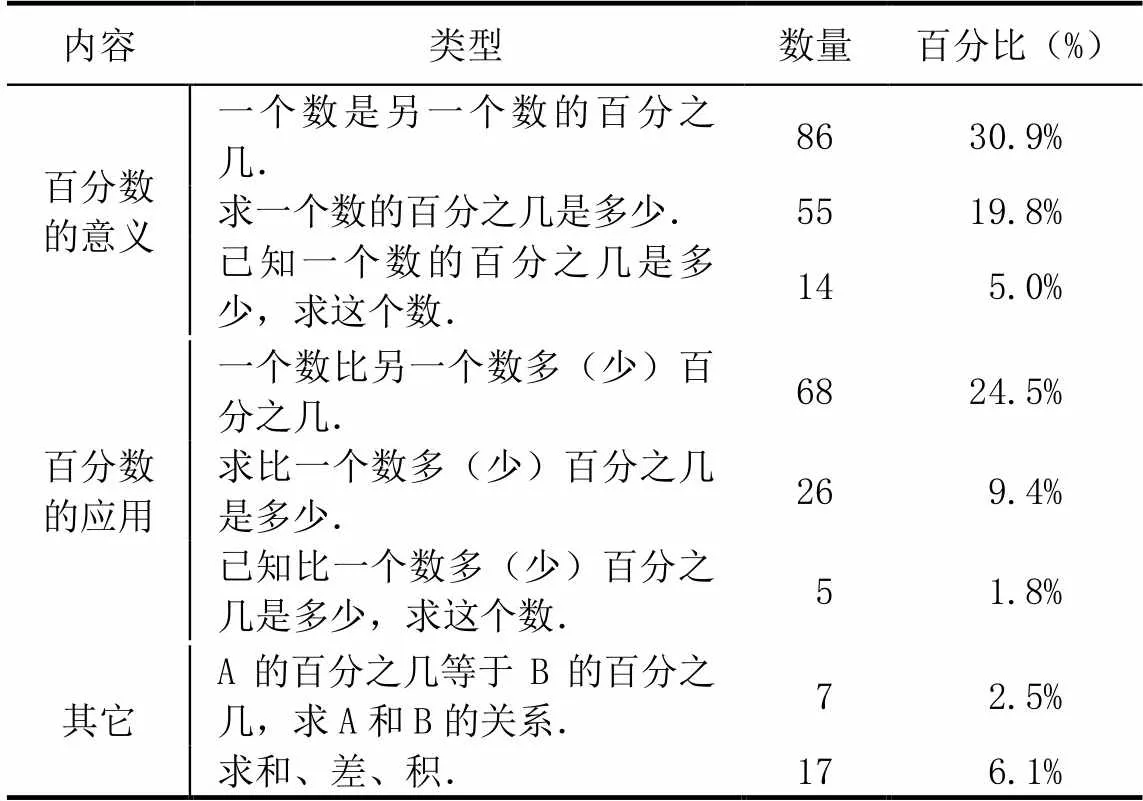
表5 教师提出问题类型的表现

3.1.4 教师提出问题涉及百分数意义的表现

根据Parker和Leinhardt（1995）对百分数的内涵界定[13]，百分数至少有5个方面的含义：数、比、比率、统计量和算子5种不同的意义．用百分数5方面的意义，对317个“情境相关问题”中“能解答的问题”进一步分类，计算每种意义下问题提出数量在317个问题中所占百分比，形成表6．例如：1.6%是5除以317得到的．

表6 教师提出问题涉及百分数意义的表现

基于表6的数据可以发现：教师提出的问题涉及了数、比和统计量3种意义，其中90.9%的问题都体现了百分数作为比这一维度的意义；7.6%的问题体现了百分数作为数的意义，如：“40%转化为小数是多少？”“40%和50%，谁大谁小？”“40%+50%=？”等；只有1.6%的问题将百分数作为统计量的意义展现出来，如：“一只股票9日价值100元，10日上涨40%，11日下降50%．11日价值几元？”在这个问题中的40%和50%表示出两个独立量的相对大小关系，体现了百分数的统计量意义．而没有问题涉及百分数作为比率和算子这两个维度的意义．

3.2 教师在问题解决上的表现

数据表明，几乎所有教师都能正确回答问卷二中的第1题，只有一位教师因为没写导致错误．其他教师都能进行正确判断，并且可以说出错误原因，即：由于雪糕店周六、周日卖出的雪糕总量不知道，因此50%与40%是无法比较的．由此可以看出，教师们知道50%和40%是两个“比”，不可以当成两个数量进行比较，若要比较，必须还要考虑50%与40%的参照量，也就是雪糕店周六、周日卖出的雪糕总量．

表7为问卷二第2题的解答情况，全部正确率为26.3%，部分正确率为60.6%，全部错误率为13.1%．部分正确是指教师能正确比较2018年和2020年工资的多少，并给出合理的解释．基于这组数据和前面编码可以看出，86.9%的教师都具有转化单位“1”的能力，知道信息中两个8%表示的是两个量的比，且知道两个比的参照量是不同的，第一个8%是2019年工资增长额与2018年工资额的比，第二个8%是2020年减少的工资额与2019年工资额的比．因此，当两个参照量不同时，两个8%不能简单地相互抵消．要想比较2018年和2020年的工资额，就需要把前面的两个8%进行转化参照量，转化成2018年和2020年工资额的比，才可以依据“比”比较两年工资额的多少．

表7 问卷二第2题解答情况

第2题中部分正确的教师均在比较多（少）几个百分点时出现错误．其中27.3%的教师直接列出算式“1-99.36%=0.64%”，得到2018年比2020年多0.64个百分点．这部分教师简单认为“1”和“99.36%”两个数据单位“1”相同，可以直接相减，反而忽略了解决“一个数比另一个数多（少）百分之几”问题时，要重新确立参照标准．其中13.1%的教师虽然意识到了要重新确立参照标准，但可能受到了语言的误导，在追问“多多少个百分点？”时，列出的算式是(1-99.36%)÷1．这部分教师受到了“多多少个百分点”的误导，于是就用“多的”作为了参照标准，导致了解决“多（少）几个百分点”最终错误．

3.3 问题提出与解决问题之间的关系

基于表8中的数据，按照解决问题3类情况进行分析，能提出4个问题的依次为92.4%、86.6%和69.2%．对数据进行相关性分析，进一步印证教师在问题提出和问题解决表现上呈现显著性相关（2=5.194，<0.001）．即解决问题能力越强的教师问题提出能力也越强，反之解决问题能力弱的教师问题提出的能力也比较弱．

卡方检验显示教师提出问题的数量和解决问题的能力并没有显著关联（2(4,=99)=5.19，=0.268）．也就是说教师问题提出的能力并不受限于他们的问题解决能力．无论教师的问题解决能力如何，他们中绝大部分教师都能提出4个问题（见表8）．即使在问题解决中完全错误的教师，仍有近70%的人能按要求提出4个难度不同的问题．

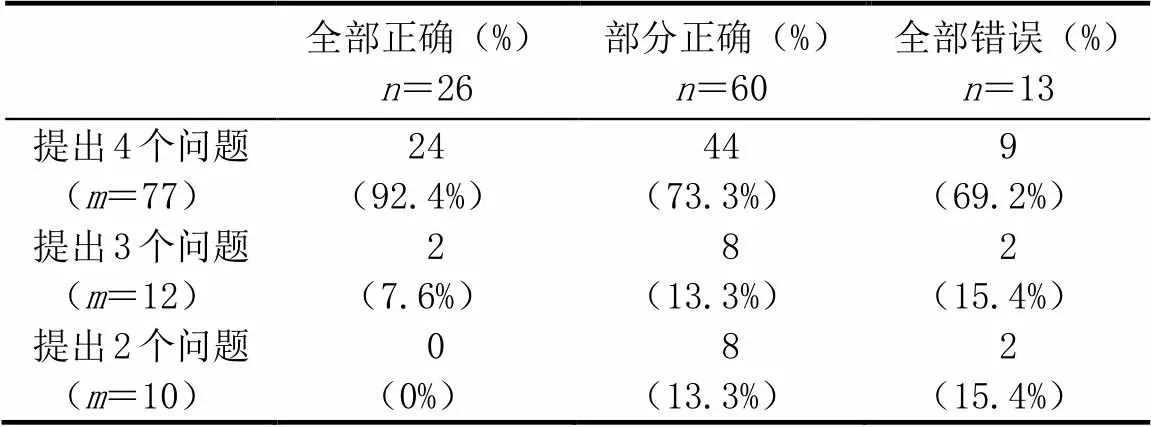
表8 教师问题提出数量与问题解决情况对比

注:表示解决问题的人数，表示问题提出的人数．

对问题解决全部错误的13名教师所提出的46个问题进行进一步的分析，发现有10位教师提出了30个与情境相关且能解答的数学问题．再次将这30个问题按步骤进行汇总，形成表9．表9中的数据显示，按照问题难度的4个级别平均的步骤为0.63、1.3、1.5、2，也是符合随着问题难度的增加，解决问题的平均步骤也在逐步增加这一特点．甚至有一名教师提出有一个需要4步才能解决的问题：“一只股票9日价值100元，10日上涨40%，11日下降50%．11日价值几元？”这一问题不仅需要多步骤的运算，还需要解答者能理解百分数有时会对应不同的单位“1”这一复杂的概念．这一问题甚至涉及了绝大部分教师都没有涉及的百分数统计量的含义（见表9）．由此可见，问题解决能力不足的教师仍有机会提出概念复杂的好问题．

表9 解决问题完全错误教师问题提出的表现

接下来，进一步对提出2个问题和3个问题的样本进行分析．22位教师提出56个问题，其中96.4%的问题为能解答的数学问题，提出2个问题的10名教师全部是能解答的数学问题，且两个问题的运算步骤上呈现明显的梯度；提出3个问题的12位教师，提出的问题中只有一个是与信息相关但不可解答的问题，绝大部分教师能够提出与情境相关且能解答的数学问题，提出的问题在运算步骤上呈现出良好的梯度．由此可见，即使有的教师不能按要求提出4个问题，但他们仍能提出有价值的数学问题．或许因为问题提出比问题解决能够提供更大的思考空间，更能调动教师积极思考提出不同难度的数学问题．但是他们对百分数概念理解的局限性仍可能会影响到提出难度不同的4个问题．因此，较之问题解决，问题提出可以更加细致全面地揭示教师对百分数概念理解的光谱，并且可以更好地促进每一位被评价者的数学思考．

3.4 不同背景教师的问题提出与其解决问题之间的关系

通过对教龄和职称的相关性分析发现，教师的教龄和职称呈非常显著的正相关（=0.731，<0.01），即教师的教龄越大，职称也就相对越高，这与中国的教师评聘制度存在明显的关系，也符合常规认识．由于教龄与职称有显著的相关关系，所以下面只讨论不同职称下教师的问题提出和问题解决情况，在必要情况下再追问教龄的相关性．

通过相关性分析发现：职称无论是与问题提出还是问题解决都未呈现显著性相关．针对问题解决，从教师职称与其在问题解决上的表现可以发现，职称越高的教师在解决百分数问题时全部错误率越低，也就意味着他们对百分数的理解越深刻．副高级教师解决问题能力最强，全部正确为41.7%，全部错误为0%；一级与二级及以下教师在解决问题上的表现可谓是旗鼓相当，但依然呈现出一级教师略逊色于二级及以下教师的现象．同时，还可以发现，不同职称教师在问题提出和问题解决上的表现是一致的．副高级教师中能提出4个问题的百分比是3个群体中最高的（91.7%），这一群体教师在问题提出上呈现出了最好的水平；二级及以下教师（79.5%）在问题提出上的表现依然略优于一级教师（72.9%）．当下小学职称结构中，能评上副高级的教师既有着丰富的教学经验，更有着优秀的师德师风，他们是教师群体中的佼佼者，副高级教师在问题提出与问题解决中的优秀表现是情理之中．一级教师是小学教师群体中年龄跨度最大的，既有刚满5年教龄的教师，又有教龄达到30年的教师；同时，在一级教师中还有一个现象，教龄越大原始学历越低，教龄在25年以上的教师都是中师毕业，他们在数学专业知识的储备方面呈现出了相对较弱水平．因此，从一定程度上可以说，教师问题提出或问题解决能力的表现是独立于现有的教师职称评级标准的．

鉴于一级教师年龄跨度比较大，从教龄的视角追问一级教师在问题提出和问题解决上的表现（见表10），研究发现一级教师随着教龄的增长：在问题解决上，能力逐渐降低；在问题提出数量上，并未呈现明显差异，其中教龄在10～25年的14位一级教师问题提出的平均数量（3.5）比其它教龄段的一级教师略少．但这14位教师提出的49个问题，均属于需要运算的问题，每位教师的问题均呈现出了问题的梯度，说明大部分教师在提出问题时，不只是为了完成数量，更对问题的质量进行了考量．因此，在考察教师的问题提出能力时，不仅要关注问题提出的数量，还要关注问题提出的质量．

表10 不同教龄一级教师在问题提出与解决问题上的表现

4 讨论

4.1 问题提出呈现出教师心中的百分数

百分数至少有数、比、比率、统计量和算子5种不同的意义（Parker，Leinhardt，1995）．通过对教师提出的问题进一步分析，发现教师心目中的百分数集中在数、比、统计量3种意义上，对比率和算子两种百分数的意义没有涉及．在全部问题中，只有极少数问题体现了百分数的数和统计量的意义，而绝大部分的问题都是作为两个数的“比”来呈现的．如：只有5位教师在提出的问题中涉及了“40%和50%，谁大谁小？”将百分数作为一个数进行比大小；只有2位教师提出了关于统计量的问题，其中一个问题是“一只股票9日价值100元，10日上涨40%，11日下降50%．11日价值几元？”在这个问题中的40%和50%表示出两个独立量的相对大小关系，体现了百分数的统计量意义．由此可以看出，教师对百分数的理解更多局限在“百分数表示一个数是另一个的数百分之几”的基本认知中，缺少对百分数概念更多维度的了解．这和中国教材中主要强调百分数是比不无关系．目前的小学教材中，缺少理解百分数概念其它维度的情境素材，比如：即使教材在学习扇形统计图时安排了用百分数进行刻画，但大部分教师依然把百分数看作一个比，并没有从百分数的统计意义去理解．而《义务教育数学课程标准（2022年版）》关于百分数有了新变化，将百分数的学习从原有的“数与代数”领域移至“统计与概率”领域，百分数将作为表达统计量的一种形式，凸显百分数的统计意义．

4.2 问题提出中实现难度梯度

数据显示，教师在围绕“40、50、%”3个信息提出问题时，力求使提出问题的难度有梯度，实现“提出4个难度不同的用百分数解决的数学问题”的要求．那么，教师是怎样实现这一目标呢？通过对每一位教师们提出的问题进一步分析，研究者发现，绝大部分教师通过百分数问题的不同类型体现问题的难度梯度，如：在简单问题环节，有37位教师提出了“求一个数是另一个数的百分之几”的问题；在中等问题环节，有33位教师提出“求一个数比另一个数多（少）百分之几”的问题．解决两种类型问题的步骤不同，第一类一步计算，第二类两步计算．还有的教师通过变化问题，增加解决问题的步骤，体现问题的难度差异．如图10，这位教师提出了4个问题，前两个问题就是百分数问题的两种类型，偏难问题和较难问题就是通过变换提问方式增加问题的难度．偏难问题是“求甲和乙的比”，而较难问题就需要求出甲和乙的比后，再进一步求甲比乙多百分之几．

还有的教师借助变换题目中百分数的参照标准，将直接信息转化为间接信息提高问题难度．

【示例】

偏难问题：有50块糖，吃了它的50%，又吃了原来的40%，还剩多少块？

较难问题：有50块糖，吃了它的50%，又吃了现在的40%，还剩多少块？

在偏难问题中的信息是“吃了原来的40%”，此时40%和50%的参照量都是50块糖，因此可以用1直接减掉50%和40%，得到剩下部分的分率．在较难问题中的信息改为“吃了现在的40%”，此时50%的参照量是50块糖，40%的参照量则是吃了50%后还剩的块数，因此，在这个问题时，需要把40%的参照量转化成和50%相同的参照量．这样一来，问题的难度增加了一个级别．

图10 提高问题难度示例

还有的教师采用增加信息来提高问题难度．

【示例】

偏难问题：一件商品降价50%后，是40元．求原价是多少元？

较难问题：一件商品降价50%后，又再一次降价40%，现价是40元．求商品的原价是多少元？

这位教师在偏难问题中，商品降价一次；在较难问题中，改为商品先后降价两次．这样通过增加一次降价，使问题的难度增加了一个级别．由此可见，这样的问题提出要求可以激发教师不同认知水平的思考．而这样的思考过程不仅可以促进他们对百分数概念的理解，同时也提供了一个全面评估他们对百分数概念理解的窗口．显然，这样层次丰富的教师概念理解能力很难在单一的问题解决过程中得以体现．

4.3 问题提出作为评价方式全面了解教师状况

数据分析表明，教师对百分数概念的理解，在问题提出和问题解决上表现的相关性是显著的．也就是说，和问题解决一样，问题提出能够帮助研究者了解教师对百分数的理解程度或类型．这不仅说明问题提出与数学理解相关，还表明了问题提出的能力与问题解决的能力具有显著的相关性．

此外，问题提出能够展现教师对概念更为丰富的理解．研究者发现，在能解答的数学问题中，既有百分数的基本概念性问题，如：“40%读作什么？”“40%和50%，谁大谁小？”“40是50的百分之几？”也有百分数的两大类（6小类）基本问题，如：“50的40%是多少？”“50比40多百分之几？”还有在此基础上衍生出一些较复杂的问题，如：“一杯糖水重50 g，糖占40%．再添多少克糖，使糖占50%．”在这个提出问题的过程中，教师主动地对百分数进行更深层次的思考，在思考中展现了教师对百分数更多的理解．因此相较于问题解决，问题提出能帮助评价者或研究者更全面地了解教师或学生对百分数的理解程度或类型．所以，问题提出同样可以作为一种教育评价的方式，只是与问题解决的评估角度有所不同．

另外，在传统的基于问题解决的评价方式下，无法解决问题的学生只能得0分，教师无从知道其中原因．而问题提出却能够为学生提供表现自己的机会，让教师了解学生对数学概念理解的程度，有助于教师根据学生存在的具体问题改进教学方法，进而实现教育评估和评价的真正目的．

除此之外，虽然多数教师都能按照要求提出问题，但问题提出的能力还有很大的进步空间．一方面从问题的严谨性看：有的教师提出的不是问题，只对问题的类型做了一般性的描述；还有的教师提出了与问题情境不兼容的问题，或者是由于信息不完整造成无法解答的问题；还有的教师提出了一些容易产生歧义的问题，如“40%比50%少多少？”这样的问题就会产生两种不同的理解，一种是求40%和50%的差，算式是50%-40%=10%；另一种是求40%比50%少百分之几，算式是(50%-40%)÷50%=20%．另一方面从问题的难度梯度看：有些教师提出的问题在难度或类型上完全没有变化，甚至问题的难度不符合难度梯度，停留在3个信息的关系变化上，并没有涉及百分数更多的内涵．研究表明，教师可以通过学习来提高问题提出的能力[1]．

4.4 百分数问题解决和和问题情景语言表征的关系

进一步的分析显示教师解决百分数问题的能力会受百分数问题数量关系的复杂性的语言表征的影响．通过前面的数据可以发现有73.7%的教师在问卷二的第2题解决“求多（少）百分点”时出现错误．从问卷二的第1题（正确率为99.0%）和第2题的第1小问（正确率为86.9%）．不仅如此，在教师提出的问题中，也有90.9%的问题都是涉及基本的“比”概念．可以看出，教师对百分数作为基本的“比”的概念是清晰的．然而当比的数量关系以及表达的语言更为复杂时，教师对百分比的概念理解和问题解决就会出现偏差．

百分数的本质是两个数量倍数关系的表达，从量的角度分析，百分数既可以表示绝对意义的量，又可以表示相对意义的量．在表示相对意义的量时，不仅能表示部分与整体之间的倍数关系，还可以表示两个独立量之间的倍数关系．当百分数作为相对意义的量进行表达时，“相差多少个百分点？”承载了复杂的数量关系，具体是指两个量的差除以其中的一个参照量，即“多多少个百分点”是两个量的差除以较小量，反之，“少多少个百分点”则是两个量的差除以较大量．如：问卷二第2题中“2019年上涨8%”就表达了2018年的工资额与2019年的工资额的关系，根据这个信息首先可以判断出2019年的工资额多，2018年的工资额少．那么，2019年比2018年多多少呢？多8%．也就是2019年与2018年工资额的差除以2018年的工资额得到的．因此，“相差多少个百分点？”是一个较复杂的相对量，这也是理解百分数表示两个量关系时的难点之一．

通过数据分析发现，有27.3%的教师把“求多（少）多少个百分点？”误以为是求两个量的差，把这个差看作了一个绝对量．其原因是受到了前面一问的影响，比较2018年和2020年工资额多少时，由于题目中两个“8%”的参照标准不同，要想比较，就需要把2020年工资额转化成以2018年工资额作为参照量．此时部分教师就误以为2018年工资额的“1”与2020年工资额的99.36%是两个绝对意义的量，可以直接相减．还有13.1%的教师虽然意识到了“求多（少）多少个百分点？”是一个相对量，但在选择参照量上出现了问题，列出的算式是(1-99.36%)÷1，误以为“多多少个百分点”就是用“多的”作为了参照标准．由此可以看出，百分数在表示两个独立数量的相对关系时，其语言表征方式也是造成意义理解的障碍之一．

[1] CAI J, HWANG S, JIANG C, et al. Problem posing research in mathematics: Some answered and unanswered questions [M] // SINGER F M, ELLERTON N, CAI J, et al. Mathematical problem posing: From research to effective practice. New York: Springer, 2015: 3-34.

[2] SINGER F M, ELLERTON N, CAI J. Problem-posing research in mathematics education: New questions and directions [J]. Educational Studies in Mathematics, 2013, 83 (1): 1-7.

[3] 中华人民共和国教育部．义务教育数学课程标准（2022年版）[M]．北京：北京师范大学出版社，2022：整体引用．

[4] 蔡金法，陈婷，孙琪琪．“问题提出”主题式培训促进小学数学教师专业发展——专访美国特拉华大学蔡金法教授[J]．教师教育学报，2022，9（5）：1-8．

[5] CAI J, JIANG C. An analysis of problem-posing tasks in Chinese and US elementary mathematics textbooks [J]. International Journal of Science and Mathematics Education, 2017, 15 (8): 1 521-1 540.

[6] CAI J, DING M. On mathematical understanding: Perspectives of experienced Chinese mathematics teachers [J]. Journal of Mathematics Teacher Education, 2017, 20 (2): 5-29.

[7] CAI J, HWANG S. Generalized and generative thinking in U.S. and Chinese students’ mathematical problem solving and problem posing [J]. The Journal of Mathematical Behavior, 2002 (21): 401-421.

[8] TICHA M, HOS PESOVA A. Developing teachers’ subject didactic competence through problem posing [J]. Educational Studies in Mathematics, 2013, 83 (1): 133-143.

[9] 宋乃庆，胡睿，蔡金法．用问题提出和问题解决测试小学生对平均数的理解[J]．数学教育学报，2020，29（3）：1-8．

[10] YAO Y, HWANG S, CAI J. Preservice teachers’ mathematical understanding exhibited in problem posing and problem solving [J]. ZDM, 2021, 53 (4): 937–949.

[11] 姚一玲，徐冉冉，蔡金法．用“问题提出”诊断和评估数学教师的概念性理解[J]．数学教育学报，2019，28（4）：30-36．

[12] 史宁中，张丹，赵迪．“数据分析观念”的内涵及教学建议——数学教育热点问题系列访谈之五[J]．课程•教材•教法，2008，28（6）：40-44．

[13] PARKER M, LEINHARDT G. Percent: A privileged proportion [J]. Review of Educational Research, 1995, 65 (4): 421-481.

[14] ISIK C, KAR T. The analysis of the problems posed by the pre-service teachers about equations [J]. Australian Journal of Teacher Education, 2012, 37 (9): 92-113.

[15] 王加明，蔡金法．用问题提出架起学生数学思考的空间——以“百分数”复习课为例[J]．小学数学教师，2021（3）：33-37．

Using Problem Posing to Diagnose and Assess Mathematics Teachers’ Conceptual Understanding of Percentages

SUN Mei1, LI Qian2, WANG Tao3, WANG Xin4, CAI Jin-fa5

(1.Hexi District Teacher Development Center, Tianjin 300203, China;2. Pingshan Road Primary School Hexi District Tianjin, Tianjin 300074, China;3. The Department of Education, The University of Tulsa, Oklahoma Tulsa 74104, USA;4. Shanghai Road Primary School Hexi District Tianjin, Tianjin 300204, China;5. The Department of Mathematics, University of Delaware, Delaware Newark 19716, USA)

Through analyzing the performance of 99 teachers’ problem posing and problem solving with percentages, this study found that the vast majority of the teachers could solve simple percentage problems. For complex percentage problems, teachers’ problem solving was related to their background: The greater the teaching experience, the higher was their success rate in solving complex percentage problems. With respect to teachers’ problem posing, most of the teachers, regardless of their background and problem-solving abilities, could pose percentage problems of various difficulty levels and demonstrated various levels of conceptual understanding of percentages. Compared to problem solving, problem posing can better reveal the spectrum of teachers’ conceptual understanding of percentages. Further analysis of the problems posed by teachers showed that most of the teachers’ understanding of percentages was still limited to the dimension of ratio rather than as statistics.

problem posing; problem solving; percentages; instructional assessment; teacher training

G623.5

A

1004–9894（2023）05–0008–09

孙枚，李欠，王涛，等．用“问题提出”诊断和评估数学教师对百分数的概念性理解[J]．数学教育学报，2023，30（5）：8-16．

2023–08–21

天津市教育科学学会“十四五”教育科研课题——提倡“数学问题提出”教学促进学生思维发展的实践研究（JK1451197B）；西南大学引进人才计划项目（SWU118118）

孙枚（1971—），女，天津人，高级教师，主要从事小学数学教育研究．蔡金法为本文通讯作者．

[责任编校：张楠、陈汉君]