多层圆柱体锚固结构中超声导波频散特征的研究

白雨佳, 张昌锁*, 牛潘宇, 张 玥, 赵金昌

(1.太原理工大学 矿业工程学院,太原 030024; 2.北京理工大学 爆炸科学与技术国家重点实验室,北京 100081)

1 引言

锚固锚杆结构中的超声导波具有频散性和多模态性等特点,所以超声导波的传播速度和衰减都会受到频率的影响[1-2]。在锚固锚杆的无损检测中,只有衰减小的激发波才能从锚杆底端反射回清晰的信号[3],进而才能判断锚固结构的质量情况。并且理论计算的超声导波频散规律常作为数值模拟和实验测试的理论依据[4-6]。因此,研究超声导波在锚固锚杆结构中的频散规律具有重要意义。

理论研究超声导波在锚固锚杆中的频散规律主要包含频散方程的建立和频散方程的求解这两大内容。频散方程是由弹性动力学以及波导结构特征和边界条件得到。如Pochhammer方程是实心圆柱杆中纵向超声导波的经典方程。对于其他更复杂的波导结构可以通过全局矩阵法[7]建立相应的频散方程。

频散方程的求解一直都是研究超声导波频散规律的难题。一方面,频散方程存在无穷多个解并且是超越方程,任意一个变量的微小变化都会影响精确解的计算。另一方面,频散方程的解通常用频散曲线表示,并且不同的曲线代表不同的模态,由于超声导波的多模态性,导致曲线之间的交叉现象会随着导波频率的增加显著增多,所以只求解某个模态对应的频散曲线就需要先解决不同模态曲线之间分类和相交的问题。

Hanifah[8]建立土中桩基的频散方程虽然很好地模拟了双层锚固结构,但无法直接拓展到多层圆柱体结构。Disperse软件[9,10]是现阶段求解多层板结构和多层圆柱体结构中超声导波频散方程的软件,并且国内外学者应用该软件对低频[11,12]和高频[1,13]导波的研究已经有了一些成果。但是Disperse软件无法计算超声导波在有限锚固厚度锚杆中传播的频散曲线,并且作为商用软件无法根据需求进行程序修改。同时,国内缺乏自主研发的相关计算软件或程序,因此建立和求解超声导波在不同锚固结构中的频散方程并实现程序化求解是研究和开发相关软件和程序的基础工作。

本文应用全局矩阵法[7]建立超声导波在多层圆柱体中的频散方程,参考Lowe[7]的求解算法编写相应的程序,然后以文献[10,12,13]的锚杆结构为算例进行计算,并与原文献应用Disperse软件计算的结果对比,验证了本文程序结果的正确性。在此基础上,计算了有限锚固厚度锚杆结构中的频散规律,弥补了Disperse软件的不足,并说明低频导波在有限与无限锚固厚度锚杆结构中的差异性及实验测试的低频导波无法用于现场无损检测。

2 超声导波在锚固锚杆中的频散方程

2.1 锚固锚杆的理论计算模型

理论计算时,锚固锚杆简化为多层圆柱体模型,并假设轴向无限长,最外层径向无限大[7]。超声导波在结构的每一层都存在沿径向方向正反的纵向体波L+和L-,垂直偏振剪切波SV+和SV-及水平剪切波SH+和SH-。锚杆、锚固剂和岩体构成的三层锚固结构的理论计算模型如图1所示。

图1 三层圆柱体锚固锚杆的理论计算模型Fig.1 Schematic diagram of the theoretical three-layer cylindrical anchored rock bolt model

2.2 锚固锚杆中的位移和应力

2.2.1 波动方程的求解

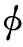
(1)

(2)

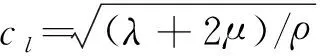
f,g1和g3与贝塞尔函数的关系如式(3),其中,gr=-gθ=g1[14]。

f(r)=L-Zn(αr)+L+Wn(αr)

g1(r)=SV-Zn+1(βr)+SV+Wn+1(βr)

g3(r)=SH-Zn(βr)+SH+Wn(βr)

(3)

2.2.2 贝塞尔函数的选择

表1 贝塞尔函数的选择规则[15]Tab.1 Bessel function selection criteria[15]

2.2.3 位移和应力表达式的矩阵式

在柱坐标系中,位移分量用势函数分量表示为

(4)

将式(3)代入式(4),可以得到位移的分量表达式。然后根据弹性动力学的几何方程和物理方程推导相应的应力表达式。由于位移和应力表达式都与贝塞尔函数以及波的幅值相关,所以,通过整理得到位移和应力的矩阵式为

Ui=DiAi

(5)

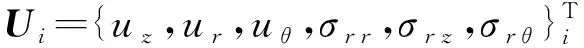
2.3 超声导波频散方程的推导

2.3.1 超声导波频散方程的通用表达式

当超声导波在一个m层圆柱体中传播时,根据位移和应力连续性条件,对于本文的多层圆柱体模型,第i层的底面(ib)和第(i+1)层的顶面((i+1)t)位移和应力分别相等,于是由式(5)可得式(6)的关系。

DibAi=D(i+1)tAi+1

(6)

整理式(6)得

(7)

m层圆柱体中共有(m-1)个分界面,每一个分界面都存在式(7)的边界条件,若模型所有的边界条件组合,就能得到包含(m-1)×6个等式和m×6个未知数的方程组。对于图1所示的三层圆柱体锚固结构,所有边界条件组成的方程组为

(8)

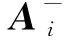
将所有未知幅值用A表示,对应的系数矩阵用全局矩阵G表示,将式(9)表示为式(10)的形式。其中,图1三层圆柱体模型的G矩阵与D矩阵关系如图2所示。

图2 三层圆柱体锚固锚杆的全局矩阵GFig.2 Generalized global matrix G of the theoretical three-layer cylindrical anchored rock bolt model

(9)

GA=0

(10)

由于式(10)是奇异方程组,所以只有当全局矩阵G的行列式为零时才能得到方程的非零解。由此可以构建超声导波在多层圆柱体锚固结构中传播的频散方程的通用表达式(11),式中k和a分别是实波数和衰减系数的另一种表示。

F(ω,k,a)=|G|=0

(11)

2.3.2 不同模态的超声导波频散方程

超声导波在多层圆柱体中传播时有纵向模态、扭转模态和弯曲模态三种不同模态,分别用L(0,m),T(0,m)和F(n,m)表示,m为模态的编号。

不同模态超声导波的频散方程存在一定差别,但都可以由式(11)得到。纵向模态和扭转模态是轴对称模态,所以将n=0代入式(11)化简后可以得到两个频散方程,其中,与ur,uz和σrr,σrz相关的是纵向模态频散方程,与uθ和σrθ相关的是扭转模态频散方程。对于弯曲模态,由于周向阶数n是正整数,所以,其频散方程形式与式(11)完全一致。

3 频散方程的求解算法

3.1 频散方程求解算法的总述

因为频散方程是超越方程并且包含圆频率、实波数和衰减三个变量,所以精确解的获取是非常困难的,取而代之的是用近似解表示,因此选择高效和准确的求解算法非常重要。本文参考Lowe[7]求解频散方程的算法编写相应的计算程序。

频散方程的求解算法包括近似解的求解和解的精确化两大部分,其重复交替进行直至得到所求范围内的所有精确解。本文以实波数频散曲线的求解来说明频散方程的求解算法,其基本流程如图3所示。

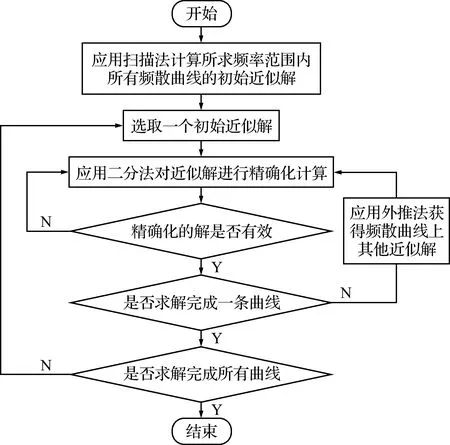
图3 频散方程求解算法的流程Fig.3 Flowchart of the dispersion equation solution

3.2 近似解的求解算法

3.2.1 初始近似解的求解

初始近似解的求解是计算频散方程的开始,其可以得到所求频率范围内所有频散曲线的初始值。

首先假设衰减初始值为零(a0=0),实波数初始值为一个常数(k=k0),那么圆频率ω就是函数F(ω,k0,0)的单一变量。令圆频率ω以合适的步长沿图4(a)箭头方向增加,并计算对应的函数绝对值|F(ω,k0,0)|,得到图4(b)所示的关系曲线。由于圆频率ω越接近频散方程的真实解,对应的函数绝对值|F|越接近零,因此可以将图4(b)曲线上所有极小值对应的圆频率ω0分别与a0和k0构成的数组(ω0,a0,k0)作为频散方程的初始近似解。因此所求频散曲线的条数与极小值点的个数对应,如图4(b)中A,B和C三个极小值点分别对应于图4(a)的三条频散曲线。

图4 初始近似解的求解过程Fig.4 Initial approximate solution solving process

3.2.2 外推法求解近似解

任意一条频散曲线的初始近似解(ω0,k0,a0)经过精确化计算得到的精确解(ω1,k1,a1)才是频散曲线的真正初始解。之后,以初始解为起点,应用外推法求解频散曲线上的其他近似解。

首先,只令初始精确解(ω1,k1,a1)的实波数k1增加(减小)一个极小的步长(Δk/1000)就得到这条频散曲线的第二组近似解,然后进行精确化计算,得到第二组精确解(ω2,k2,a2)。之后,应用线性外推法获得新的近似解,实波数增加(减小)Δk,圆频率和衰减根据式(12)线性外推公式计算得到,其中n为近似解的编号。同样的,得到近似解后,应用精确化算法计算相应的精确解。

ωn=2ωn-1-ωn-2,an=2an-1-an-2

(12)

得到一条频散曲线上的6个精确解之后,外推法改用精度更高的二次外推法,计算过程如图5所示。当计算第n+1个近似解时,实波数kn增加(减小)Δk,圆频率和衰减则以第n-1,n-3和n-5个精确解为基础,通过二次外推公式(13)计算对应的近似解。与线性外推法相比,二次外推法是由不相邻的三个精确解计算新的近似解,因此,可以有效避免不同频散曲线在交叉位置的错误追踪。

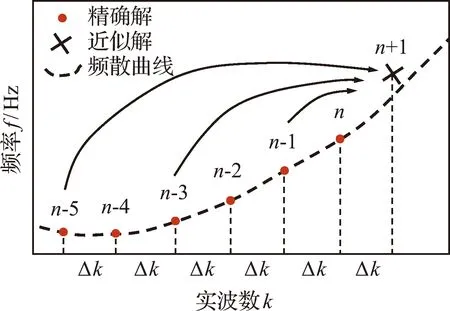
图5 二次外推法Fig.5 Explanatory diagram of quadratic extrapolation

ωn+1=ωn-5-3ωn-3+3ωn-1

an+1=an-5-3an-3+3an-1

(13)

3.3 精确解的求解算法

3.3.1 近似解的精确化计算

近似解的精确化就是在近似解的基础上保持实波数k不变,利用二分法寻找能够满足频散方程解的判断条件的圆频率ω和衰减值a。该算法包含圆频率ω和衰减a分别作为单一变量的两部分,其计算过程完全相同,只是变量类型不同,并且这两部分重复交替进行,直到满足解的判断条件结束。

在单一变量为圆频率ω的二分法计算中,首先需要根据当前近似解的值确定圆频率的初始计算区间,要求这个区间包含能使函数绝对值达到极小值点的圆频率。圆频率初始计算区间的求解过程如图6所示。首先,将圆频率近似解ωa0分别增加和减小一个极小的步长得到两个圆频率值,计算其对应的函数绝对值并选择绝对值更小的方向作为圆频率ωa0的变化方向。如图6中ωa0需要增加一个步长Δω才能得到可以使函数绝对值更小的圆频率ωa1。同样的,在位置1也使圆频率ωa1分别增加和减小一个极小的步长来判断增减方向。由于图6中ωa1的增减方向与前一个的方向相同,所以需要继续增加Δω得到下一个圆频率和其对应的增减方向。重复上述过程直到新的圆频率对应的增减方向与前一个圆频率的增减方向相反,如图6中ωa2与ωa1的增减方向相反,说明这两个圆频率值确定的范围包含了可以使函数绝对值达到最小的圆频率ωmin,所以,这个范围就是圆频率进行二分法计算的初始区间。

图6 圆频率初始区间的求解过程Fig.6 Determination of the initial range endpoint values

得到圆频率的初始区间后,将二分计算区间的左端点、中间点和右端点分别表示为pl,pc和pr,并取[pl,pc]和[pc,pr]的中点为plm和prm,得到初始区间上等距分布的5个计算点。计算这5个点的函数绝对值,选择绝对值最小的点作为二分后新区间的中间点pc,并将与其相邻的两个点作为新区间的左右端点pl和pr,这样通过一次二分计算后就得到了长度是原区间一半的新二分区间。

每次得到新的pc后,都需要进行解的有效性判断,若满足判断条件,就实现了近似解的精确化,那么就将此时的圆频率、衰减和实波数作为频散曲线上的一组精确解输出。若不满足判断条件,就需要重复二分法过程继续缩小区间范围,直到满足解的有效性判断条件或者区间范围小于预先设定的容差值。设置容差值的目的是为了让程序无条件收敛而不出现死循环,本文圆频率的容差值为1 Hz,衰减的容差值为10-4nepers/m。

当圆频率的二分法计算以区间范围小于容差值而结束时,说明当前圆频率的增减已经无法使函数F更接近零,因此保持圆频率不变,将衰减作为单一变量重复上述二分法计算过程。

3.3.2 解的有效性判断

在应用二分法将变量逐渐逼近精确解的过程中,对应的函数值也在复数域逐渐趋近于零。理论上,若将频散方程的精确解代入频散方程函数F(ω,k,a)中,对应的函数值为零并与复数域中的原点重合。但是,由于计算误差和计算精度等问题的存在,函数值无法完全与原点重合。所以需要用其他的标准判断是否得到了频散方程的解。

因为频散方程是关于三个变量的超越方程,变量的微小变化就会使函数值发生大幅度变化,因此无法用某个具体的容差作为判断当前变量是否满足频散方程的解的条件。所以本文采用文献[7]的角度法对解的有效性进行判断。首先,将二分法中计算区间两端点pl和pr对应的变量值分别代入函数F(ω,k,a)中,并得到函数值的实部和虚部。然后将这两个函数值表示在复数域中,如图7所示,计算其与原点连线的夹角。当夹角大于90°时,表明当前区间中心点pc的变量值就是频散方程的解,若夹角小于90°,说明还未找到频散方程的解,需要继续进行二分法计算。

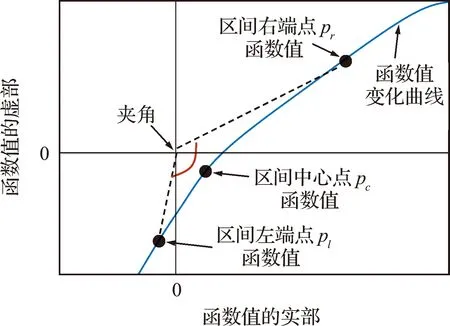
图7 角度法判断解的有效性Fig.7 Solution validity determination using the angle evaluation method

4 对比验算

应用本文建立超声导波在多层圆柱体中传播的频散方程和求解频散方程的算法,编写相应的程序,计算文献[10,12,13]不同锚固锚杆结构的频散规律,并与原文献中应用Disperse软件计算的结果进行对比,从而验证本文编写程序的正确性。

4.1 自由锚杆模型

首先以文献[13]的直径为22 mm的自由锚杆为对象,应用本文的程序计算0 MHz～3 MHz范围内的衰减频散曲线,并与原文应用Disperse软件计算的结果进行对比,如图8所示。可以看出,在频率为0 MHz～3 MHz且衰减小于40 dB/m的范围内,两种结果中都有17条衰减频散曲线,并且曲线变化形式和极小值对应的频率都能吻合,表明本文的程序可以正确计算自由锚杆的频散曲线。

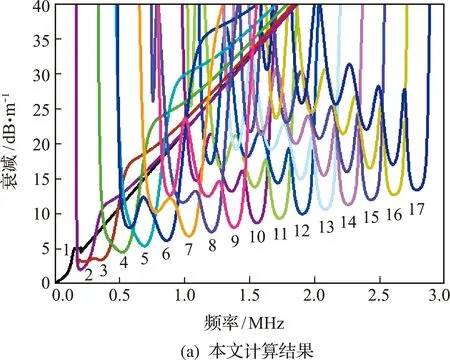
图8 自由锚杆衰减频散曲线Fig.8 Attenuation-dispersion curves of a free bolt

4.2 双层锚固锚杆模型

4.2.1 直接锚固于无限岩体的双层圆柱体模型

以文献[10]的锚杆直接锚固于无限岩体的双层圆柱体模型为对象进行计算,得到图9(a)所示的衰减频散曲线。

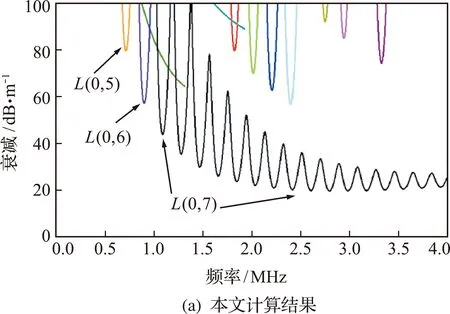
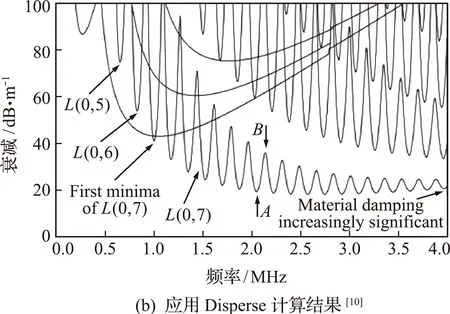
图9 双层圆柱体锚固结构的衰减频散曲线Fig.9 Attenuation-dispersion curves of the two-layer anchored rock bolt

应用Disperse软件的计算结果[15]如图9(b)所示。通过对比可知,在频率小于4 MHz、衰减小于100 dB/m的范围内,两种结果都包含了L(0,5),L(0,6)和L(0,7)三条频散曲线,并且其变化形式完全相同。L(0,5)和L(0,6)分别存在一个衰减极小值,而L(0,7)存在多个衰减极小值并且随着频率的增加逐渐减小和趋于平缓。由于L(0,7)曲线极小值点的衰减相对较小,所以可以优先选用这些频率的超声导波作为无损检测的激发波。

4.2.2 水泥砂浆双层圆柱体锚杆模型

以文献[12]的砂浆锚杆为对象进行计算,这种模型的结构是双层锚固结构。计算的衰减频散曲线[12],如图10(a)所示,应用Disperse软件的计算结果[12]如图10(b)所示。对比发现,当频率小于500 kHz,衰减小于500 dB/m 时,这两种方法都能得到五条衰减频散曲线。L(0,2)～L(0,5)的变化形式以及频率与衰减的对应关系基本相同,但L(0,1)曲线在150 kHz～200 kHz范围内有较大差别,图10(a)中150 kHz～200 kHz范围内的衰减值几乎不变,然后在200 kHz以后突然减小;而图10(b)中频散曲线在150 kHz附近是一个极大值点。出现这样的结果说明本程序在计算锚固锚杆结构这类复杂结构的超声导波频散曲线时还存在一些问题,需要继续调试。同时,这也说明了精确求解频散方程确实很困难。

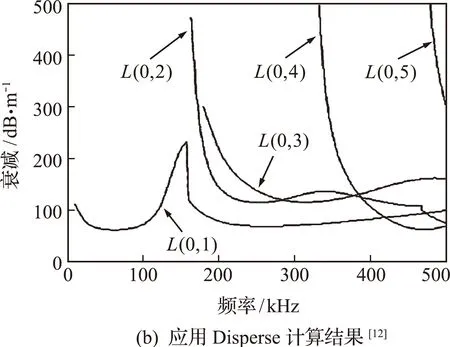
图10 水泥砂浆锚固结构的衰减频散曲线Fig.10 Attenuation-dispersion curves of the mortar anchored rock bolt model

5 有限锚固厚度锚杆模型

Disperse软件开发团队的Beard[10]利用Disperse软件分别计算了自由锚杆和锚固于无限岩体锚固锚杆中的超声导波频散曲线,但未计算用于实验研究的有限锚固厚度的锚固锚杆中的频散曲线。在实验测试中,Beard采用波浪形边界的有限锚固结构代替实际的无限岩体,并得到了低频测试波在锚杆底端的反射信号,认为低频导波的衰减较小,能够用于实际检测。但该结果与其利用Disperse软件计算低频导波在无限锚固介质中的衰减特征及本文的计算结果(图9)均不吻合。

为了更全面认识锚固锚杆结构中超声导波的传播规律,本文也计算了用于实验研究的有限锚固厚度锚杆结构中的超声导波频散曲线。本文计算用的锚固锚杆直径为20 mm,外径为200 mm,锚固体为混凝土材料,材料参数列入表2。

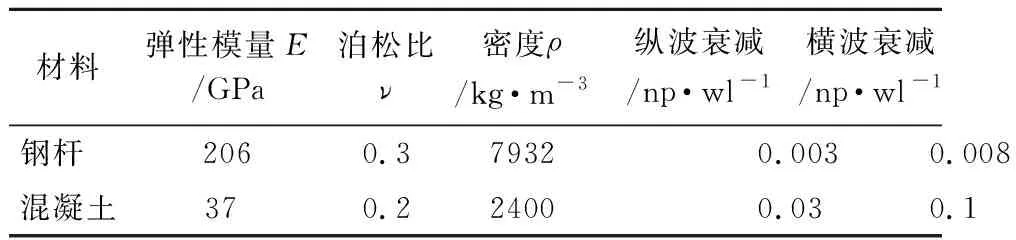
表2 实验模型的材料参数Tab.2 Experimental model material properties

根据表2计算该模型的超声导波衰减频散曲线如图11所示。其中包含了109条衰减频散曲线,即109个模态,表明超声导波在有限锚固厚度锚杆中的传播非常复杂。可以看出,低频导波的衰减确实很小,与Beard[10]的实验测试结果一致,因此,本文计算结果弥补了Beard未应用Disperse软件进行相关计算的不足。与图9对比可以看出,有限与无限锚固结构中低频导波的衰减特性有巨大差异。因此,由有限锚固结构中获得的衰减小的低频测试波并不能用于现场无限锚固厚度锚固锚杆的无损检测,即实验测试得到的低频导波不具有普适性。

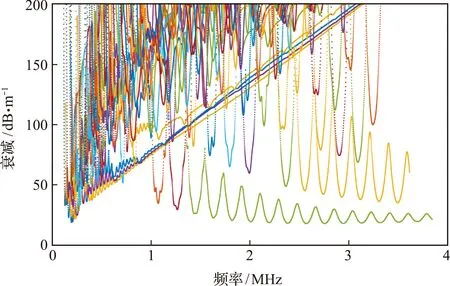
图11 有限锚固厚度锚固锚杆衰减频散曲线Fig.11 Attenuation-dispersion curve of anchor rod with finite anchor thickness

6 结 论

本文采用全局矩阵法建立了多层圆柱体模型中超声导波的频散方程,应用高效频散方程求解算法,自主编写了高精度求解程序。然后对文献中不同锚杆结构中纵向模态超声导波的传播规律进行计算,并与原文使用Disperse软件的计算结果吻合,验证了本程序的正确性。

计算结果表明,对于结构比较简单的自由锚杆,本程序可以得到与Disperse软件计算结果完全一致的频散曲线,表明本文采用的频散方程建立方法和求解频散方程的算法具有可行性。对于结构比较复杂的锚固锚杆,本程序也可以得到与Disperse软件基本吻合的计算结果,但同时也因为锚固锚杆结构的频散方程更加复杂,使得个别频散曲线与原文献无法完全对应,因此本程序仍需改进。本程序也计算了有限锚固厚度锚杆结构中超声导波的传播规律,弥补了Disperse软件未曾进行相关计算的不足。计算结果表明,有限与无限锚固结构中低频导波的衰减性差异巨大,并不能将实验模拟中衰减较小的低频导波用于现场锚固锚杆结构的无损检测。

总体上,本文编写的程序很好地解决了频散曲线求解中的分类和相交问题,能求解特定模态的频散曲线,针对实验室低频导波的结果不具有普适性这一问题,给出了合理的计算模型与结果。