外载荷作用下塔器开孔补强计算探讨

袁 博，许学斌，王小鹏

(华陆工程科技有限责任公司，陕西 西安 710065）

塔器是石油化工行业中的常用设备，在进行塔器设计时，除应考虑内压、外压和液柱静压力外，还应考虑风载荷、地震载荷及容器自重等其他外载荷［1］。操作工况下，塔体上的轴向力由计算压力、容器自重和最大弯矩引起，最大弯矩选取风载荷+偏心载荷和地震载荷+25%风载荷+偏心载荷2种情况下的最大弯矩，当塔体较高且直径较小时，塔体上的轴向力往往远大于由压力载荷引起的环向力，塔器的强度设计取决于风载荷、地震载荷等弯矩载荷而非压力载荷［2］。

为满足工艺操作、塔体制造、内件安装及检查、维修等需要，通常会在塔体不同高度、不同方位开设人孔和管孔［3］。当风载荷和地震载荷起主要作用时，国内压力容器计算软件SW6中对塔体上开孔补强的计算采用的是等面积法 （仅考虑压力载荷并未考虑风载荷和地震载荷的作用［4-5］），这种计算方法有时是偏危险的。本文以某一项目中的汽提塔作为工程实例，分别采用等面积法和组合应力法计算塔体上的开孔补强并将计算结果加以对比，提出以组合应力法和等面积法相结合的方法进行塔体的开孔补强计算。

1 塔器开孔补强等面积法局限性

作为开孔补强的常用计算方法，等面积法的设计思想为，有效范围内实际的补强面积大于塔体由于开孔所需的补强面积。而对于风载荷和地震载荷起控制作用的塔体，等面积法补强计算存在以下局限性。

（1）等面积法中塔体和接管的计算厚度是由压力载荷计算得来，并未考虑风载荷和地震载荷。当风载荷和地震载荷作为主要载荷时，塔体的计算厚度应通过先假定，然后不断试算得出［6-7］。文献［6-7］中考虑到了风载荷、地震载荷、偏心载荷及容器自重，通过SW6软件不断试算，虽然准确算出了塔体的计算厚度，但最后仍然按照等面积法进行开孔补强设计。

（2）等面积法是计算各受压元件的截面积，当风载荷和地震载荷作为主要载荷时，塔器的主要应力为 NB/T 47041—2014《塔式容器》［8］中最大弯矩引起的轴向应力σ3，而非压力引起的轴向应力σ1，而轴向应力σ3的大小主要取决于塔体的抗弯截面系数而非塔体的截面积。

（3）等面积法是考虑压力载荷作用下的补强计算方法，压力载荷作用时，塔体内的主要应力是环向应力，其计算截面为塔体的纵向截面。当风载荷和地震载荷作为主要载荷时，塔体内的主要应力是轴向应力，计算开孔补强时的计算截面应为塔体的横向截面。

2 塔器开孔补强组合应力法

塔器属于高耸结构，它承受的载荷除压力载荷外，尚有风载荷、地震载荷、偏心载荷与重力载荷等［9］。压力较低时，风载荷或地震载荷就成为影响塔器安全运行的主要载荷。而这些载荷在塔体截面中产生的应力是弯曲应力，一般来讲，在相同的风载荷与地震载荷条件下，塔器的高度越高，高度与直径之比越大，塔体的弯曲应力越大［10-11］。根据NB/T 47041—2014，塔体截面轴向应力由内压或真空引起的轴向应力σ1、操作或非操作时重力及垂直地震力引起的轴向力σ2以及弯矩引起的轴向力σ3这 3部分组成，应分别按式（1）～式（3）计算，各物理量具体含义同NB/T 47041—2014。需说明的是，这些计算式中未考虑塔体开孔处几何形状的变化，因此计算开孔处的轴向应力时公式会有所不同。

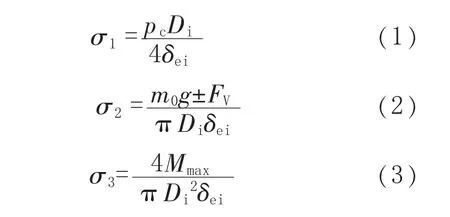
圆筒的最大组合压应力校核公式为：

圆筒的最大组合拉应力校核公式为：

式（4）～式（7）中，ϕ为焊接接头系数； ［σ］cr为许用压应力，［σ］t为许用拉应力，MPa；K 为载荷组合系数，取1.2。在风载荷和地震载荷作用下计算塔体组合拉、压应力时，许用应力为原许用应力乘以1.2，即计算时将许用应力提高20%。

式（1）～式（3）虽然准确计算出了塔体截面的轴向应力，但是将塔体截面作为环形截面，未考虑开孔对截面的削弱作用。本文提出的组合应力法是将开孔处的截面作为危险截面，考虑开孔对塔体的削弱作用，先准确计算出开孔截面的组合面积和组合抗弯截面系数，然后计算开孔截面的轴向应力 σ1、σ2、σ3，最后按式（4）～式（7）组合应力校核原则对开孔截面组合轴向应力进行校核。

需特别说明的是，开孔处的组合抗弯截面系数主要取决于惯性矩，由于开孔处的接管法兰以及后端管线的惯性矩不可能无限制地参与组合惯性矩的计算，因此参考GB/T 150.3—2011《压力容器 第 3部分：设计》［12］中4.5.1.1节圆筒体有效段的计算公式，来计算接管惯性矩的有效段长度 L，即（Do为接管外径，δe为接管有效厚度）。

3 塔器开孔截面组合应力计算

3.1 内压或真空引起的轴向应力σ1

σ1仍采用 NB/T 47041—2014中提供的公式，即式（1）进行计算。

3.2 操作或非操作时重力及垂直地震力引起的轴向力σ2

考虑塔体开孔处几何形状的变化，按下式计算开孔处的轴向应力σ2：

式中，A为开孔截面的组合面积，mm2。按 NB/T 47041—2014，FV仅在最大弯矩为地震弯矩参与组合时计入。

塔体开孔截面见图1。图1中D为塔体外径，d为塔体内径，b为接管内径，δ为塔体厚度，δt为开孔接管厚度，s为接管根部至设备中心距离。

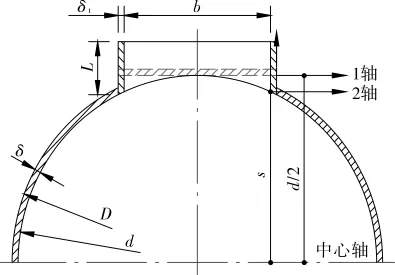
图1 塔体开孔截面示图

开孔截面的组合面积A由塔体的截面积A1和接管的截面积A2组成，其中塔体的截面积A1等于原塔体截面积减去开孔去掉的截面积 （图1中虚线部分），即 A1=πdδ-（b+2δt）δ，接管的截面积A2=2Lδt，则开孔截面的组合面积为：

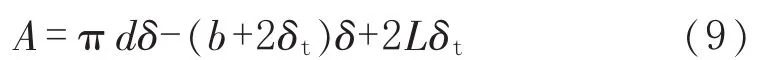
3.3 弯矩引起的轴向力σ3

考虑塔体开孔处几何形状的变化，按下式计算开孔处的轴向应力σ3：

式中，W为开孔截面的组合抗弯截面系数，mm3。

在计算开孔截面的组合抗弯截面系数W之前，要先求出开孔截面相对于中心轴的组合惯性矩I。与开孔截面的组合面积A类似，开孔截面的组合惯性矩I分为塔体的惯性矩I1和接管的惯性矩 I2，其中塔体的惯性矩 I1=I′-I″，I′为塔体环形截面的惯性矩，I″为因开孔削弱的惯性矩 （等于图1中虚线部分对中心轴的惯性矩）。假定R为塔体的内外径比值（R=D/d），对于薄壁容器选取R≈1［13］。

塔体环形截面的惯性矩I′计算公式：

开孔削弱的惯性矩I″计算公式：

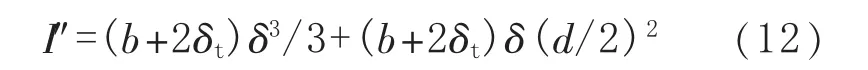
根据材料力学中的平行轴定理［14］，I″包括1轴的惯性矩（式（12）等号右侧第一项）和中心轴的惯性矩（式（12）等号右侧第二项）。将式（12）等号右侧第一项与第二项进行对比，其比值为4δ2/3d2＜＜1，说明第一项在 I″中所占比重非常小，在满足工程设计误差范围内可以忽略。因此塔体的惯性矩可表示为：

4 塔器开孔补强实际工程算例

4.1 设计参数

以某项目中汽提塔为例，分别采用等面积法和组合应力法对塔体开孔补强进行计算。汽提塔基本设计参数为，设计压力1.8 MPa、设计温度80℃、焊接接头系数 0.85［15］、基本风压 0.36 kPa、地震设防烈度 7（0.15g）、塔盘层数 48 层（浮阀）、填料高度6 000 mm、塔体直径1 400 mm、塔体高度 51 750 mm、裙座高度5 000 mm、塔体下段厚度18 mm。塔器主体材料为S30408，其许用应力137 MPa。在距离塔体下封头切线550 mm处开设人孔，人孔的尺寸为ϕ530 mm×10 mm。塔体外径D=1 436 mm，塔体内径d=1 400 mm，塔体厚度 δ=18 mm，接管内径 b=510 mm，开 孔 接 管 厚 度 δt=10 mm，许 用 拉 应力 ［σ］t=139.74 MPa，许用压应力［σ］cr=118.12 MPa。

4.2 SW6软件计算结果

经SW6软件计算得到的塔器操作质量为61 254.1 kg （操作工况）、44 666.2 kg （检修工况），开孔截面最大弯矩 Mmax=2.602×109N·m（由风弯矩控制）。塔体最大组合压应力101.13 MPa，小于许用值118.12 MPa；塔体最大组合拉应力为123.38 MPa，小于许用值139.74 MPa。开孔削弱所需的补强面积3 705 mm2，有效补强范围内的补强面积7 415 mm2，有效补强范围内的补强面积大于开孔削弱所需的补强面积，塔体厚度和开孔补强计算均合格。

4.3 组合应力法校核结果

按式（9），开孔截面组合面积 A=71 222 mm2。按照式 （17），开孔截面的组合抗弯截面系数W=22 504 590 mm3。 按式（1），由内压引起的轴向应力σ1=35.58 MPa。按式（8），操作工况和检修工况下由重力引起的轴向应力σ2分别为8.43 MPa和6.15 MPa。按式（10），由弯矩引起的轴向应力σ3=115.62 MPa。

则塔体最大组合压应力 σ2+σ3=121.77 MPa（参照文献［11］，此处 σ2取检修工况的值），大于许用值118.12 MPa；塔体最大组合拉应力σ1-σ2+σ3=142.77MPa（参照文献［11］，此处 σ2取操作工况的值），大于许用值139.74 MPa。塔体组合压应力和组合拉应力校核均不合格。

4.4 开孔补强方法

4.4.1 增大接管壁厚

将接管壁厚增大到18 mm，按组合应力法各公式计算得到开孔截面组合面积A=74 840 mm2，开孔截面的组合抗弯截面系数W=24 939 804 mm3，σ1=35.59 MPa，操作工况下σ2=8.0 MPa，检修工况下 σ2=5.85 MPa，σ3=104.3 MPa。

塔体最大组合压应力σ2+σ3=110.15 MPa，小于许用值118.12 MPa；塔体最大组合拉应力σ1-σ2+σ3=131.89 MPa，小于许用值 139.74 MPa。塔体组合压应力和组合拉应力校核合格。

4.4.2 增加补强圈

增加尺寸为ϕ840 mm×18 mm的补强圈，同理，按组合应力法各公式计算得到开孔截面的组合面积A=76 982 mm2，开孔截面的组合抗弯截面系数 W=23 895 938 mm3，σ1=35.59 MPa，操作工况下的 σ2=7.8 MPa，检修工况下的 σ2=5.69 MPa，σ3=108.9 MPa。

塔体最大组合压应力 σ2+σ3=114.59 MPa，小于许用值118.12 MPa；塔体最大组合拉应力σ1-σ2+σ3=136.69 MPa，小于许用值 139.74 MPa。塔体组合压应力和组合拉应力校核合格。

4.4.3 对比分析

虽然增大接管壁厚和增加补强圈均可使塔体组合应力校核合格，但对比计算结果可以发现，增大接管壁厚的补强效果要好于增加补强圈的。这是由于增大接管壁厚可以更大程度提高开孔截面的惯性矩，进而增大组合抗弯截面系数，从而有效降低由弯矩引起的轴向应力σ3。

5 结语

如果只按等面积法进行塔器开孔补强计算，在塔体计算厚度、补强计算截面以及应力校核上都有局限性。当风载荷和地震载荷较大时，塔体上轴向应力往往较大，等面积法没有充分考虑开孔对塔体上轴向力的削弱。当塔器计算厚度由轴向力决定时，等面积法存在不安全因素，尤其在开孔位于塔器计算危险截面附近（如厚度、直径、材料变化等截面）、开孔率较大或开孔数量较多、开长圆孔且长轴垂直于塔体轴线以及开孔接管壁厚与塔体壁厚比值较小等情况下是偏于危险的。应先通过等面积法进行设计，然后采用组合应力法进行校核。

工程实例计算证明，当开孔导致塔体轴向应力超过许用应力值时，增大接管壁厚的补强效果要好于增加补强圈。