子集模拟的混合采样算法

2023-10-26廖子涵李宾宾

计算力学学报 2023年5期

廖子涵, 李宾宾*

(1.浙江大学伊利诺伊大学厄巴纳香槟校区联合学院,海宁 314400;2.浙江大学建筑工程学院,杭州 310058)

1 引言

实际工程中,结构面临几何尺寸、材料属性、边界条件和荷载等不确定性因素。因此,可靠性分析对于结构设计优化和结构安全性评估等工作具有重要意义。其中结构失效概率的计算通常通过以下三种方式求解,(1) 近似估计法,如基于功能函数泰勒展开的可靠度分析方法。该方法对于高度非线性问题与多失效点问题不适用。(2) 蒙特卡洛积分法,包括直接蒙特卡洛模拟及马尔科夫链蒙特卡洛模拟MCMC(Markov Chain Monte Carlo)法。此类方法具有良好的通用性与准确性,但计算代价较高。(3) 代理模型法。常用的代理模型包括响应面法[1]、高斯过程模型[2]、Kriging模型[3]和支持向量机[4,5]等。当参数维度较大时,该方法需要提取特征进行降维分析,这必然导致信息丢失且无法确保失效概率估计的无偏性。

为解决高维参数空间下失效区域概率估计问题,Au等[6]提出子集模拟算法,利用条件概率引入中间事件,自适应地将一个小的失效概率分解为一系列相对较大的条件概率的乘积。通过MCMC采样,将样本经由中间事件进行一系列筛选与生成,滚动地不断接近参数空间中的失效区域。其作为一种较为高效的数值计算方法,广泛应用于各类结构可靠度的计算。此外,由于可靠度问题(小概率事件)、优化问题(极值事件)和贝叶斯更新问题(极限状态方程可以看作一类特殊的似然函数)之间存在联系,子集模拟近年也通过改造逐渐应用在多个领域。Suo等[7]将非支配排序引入样本排序的规则,实现多目标优化。广义子集模拟[8]将子集模拟法的应用推广到多极限状态方程与时变可靠性分析领域[9]。

子集模拟中,MCMC算法的使用在增强采样效率的同时导致样本之间存在相关性。这种相关性不仅会增大条件概率的计算方差,还会使得算法的遍历性下降,样本无法对失效区域进行有效覆盖,进而影响单次模拟结果的可信度。目前降低样本相关性主要体现在参数优化和MCMC采样算法优化两个方面。其中相关参数的优化集中于条件概率的选取,条件概率越低,模拟收敛的速度越快,但马氏链之间相关性较高,遍历性下降。相反的,条件概率越高,算法遍历性越好,但层与层之间的相关性上升,模拟所需计算量增大,子集模拟算法的优势削弱。

采样器的更新优化是近年来子集模拟发展的主要方向。在最初的子集模拟中,Au等[6]采用的是改进MH(Metropolis Hastings)算法。为了减少马尔科夫链内的相关性,Santoso等[10]提出重复采样版本的MH采样法,通过重复采样保证产生的待选样本与之前样本不同,然而该方法的人为选择性,导致MH算法中的可逆性条件不能满足,生成的样本虽然相关性降低,但分布与目标分布之间存在误差[11]。此外,通过对种子样本进行拉伸采样[13],也能从马尔科夫链的起始点降低链与链之间的相关性。更复杂地,Miao等[13]提出再生自适应子集模拟算法,通过随机再生建议分布以及延迟拒绝算法,克服burn in问题并且尽可能多地获得独立样本。然而,在子集模拟中马尔科夫链的种子分布已经自动满足目标分布,因此再生建议分布理论上对于解决burn in问题不起作用[14]。为了方便在高维空间中对多种分布组成的概率密度函数进行蒙特卡罗采样,Papaioannou等[11]提出自适应条件采样aCS(adaptive Conditional Sampling),将变量θ通过Nataf变换[15]转化为独立和标准正态分布的变量u,并在标准正态空间U中进行采样与数值积分。该方法在简便性与准确性方面都较为突出,获得了广泛的应用。为了提升样本探索空间的效率,将Hamiltonian采样嵌入子集模拟法中[16,17],该方法基于功能函数的梯度矩阵,提升样本向函数值较高的区域移动的速度,但同时会增加计算梯度矩阵的负担。连续空间转换[18]通过控制变量方法先给出一个粗略的失效概率估计值,再通过修正项进行细化修正,通过扩大样本分布的方差以增加样本的遍历性。

2 子集模拟法

2.1 子集模拟法

定义n维结构参数θ∈n及其概率密度函数fn(θ),对于代表结构失效模式的极限状态方程g(θ),结构失效概率可表达为

(1)

式中IF(θ)为失效事件F={θ∈n∶g(θ)≤0}的指示函数,即

(2)

式(1)可通过直接蒙特卡洛采样积分方式近似求解,然而结构失效一般为小概率事件,失效域仅占参数空间的极小部分,大量样本点落在安全域,造成计算资源的严重浪费,特别是在参数θ的维度n很大的情况下。

子集模拟算法将结构失效事件F表示为一系列逐级包含的失效事件的交集

(3)

F1⊃F2⊃…⊃FM=F

(4)

式中Fj={θ∈n∶g(θ)≤bj},b1>b2>…>bM=0。利用条件概率的性质,原结构失效概率转化为一系列条件失效概率的乘积

(5)

式中F0={θ∈n∶g(θ)≤∞}为确定事件,即Pr(F0)=1,Pr(F1|F0)=Pr(F1)。每一层的条件失效概率计算可参照式(1)进行,

(6)

对应的条件概率密度函数为

(7)

由于条件概率密度函数fn(θ|Fj-1)不是标准的概率分布,如何实现其快速有效采样成为实现失效概率估计的关键。基于这一观察,子集模拟可看作是一种自适应重要性采样算法,从初始概率密度函数fn(θ)出发,通过给定条件失效概率p0=Pr(F1|F0)(一般取为0.1或0.2)确定分界点b1和对应失效域F1,然后以失效域F1内采样点作为种子,基于MCMC原理实现fn(θ|F1)的采样并进而确定新的分界点b2和失效域F2,以此类推,直至达到目标失效域FM=F。从上述过程可以看出,子集模拟选用MCMC采样,每一层样本基于上一层传递下来的种子样本,从而实现条件概率密度函数fn(θ|Fj-1)的自适应采样,且种子本身满足分布fn(θ|Fj-1),大大提升了候选样本的接受率。

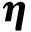
图1 样本运动Fig.1 Sample movement

(8)

式中Tn(·|·)为转移概率密度。通过随机数与接受率比较后筛选得到候选样本ξ。此时,候选样本的总体分布介于fn(θ|Fj-1)与fn(θ)之间,近似于从fn(θ|Fj-1)扩散到fn(θ)的过渡阶段。第二步,基于指示函数IFj-1(θ)对候选样本ξ进行二次筛选,将超出边界的样本点收缩回初始点,得到更新后的样本θk+1,即

(9)

(10)

即满足细致平衡条件。式(10)利用IFj-1(θk)=1和函数min{·}的性质。需要指出的是,直接应用MCMC采样并不适用于高维随机采样,也就是存在高维灾难问题,本文将简要介绍两种常用的高维采样算法,从而使得子集模拟能够解决高维可靠度估计问题。

2.2 高维随机采样

2.2.1 改进MH采样

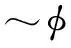
(11)

2.2.2 自适应条件采样

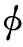
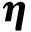
(12)

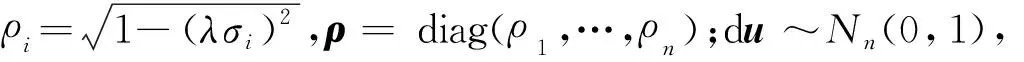
3 混合采样算法

3.1 椭圆切片采样

椭圆切片采样ES(Elliptical slice sampling)[19]为切片采样在正态空间的一种特殊形式。与条件采样和哈密顿采样类似,首先对现有样本u进行扰动

v=ucosβ+dusinβ

(13)

式中β～U[0,2π],du～Nn(0,1)。设定下一步角度选取的上下界[βmin,βmax]=[β1-2π,β1]。使用公式对侯选样本进行筛选,若拒绝,则将β1设定为分布的上界或下界

βmin=β(β<0)
βmax=β(β≥0)

(14)

基于更新后的上下界均匀随机取值β并重复以上步骤,直到样本接受。该方法本质上为一种收缩条件采样(或正态分布下的轨迹收缩哈密顿采样)。将边界条件的筛选步骤与新样本的生成结合在一起,保证新产生的样本在满足边界条件的前提下互相不重复,增加了等效独立样本的数量,并且每次对角度的搜索从全分布出发,增强了样本的遍历性。相对的,椭圆切片采样收缩过程中拒绝步骤的嵌入也会带来较大的计算量。如图2所示,椭圆切片采样在单次产生步骤的样本范围大于自适应条件采样,带来较好遍历性的同时降低收缩步的接受概率。

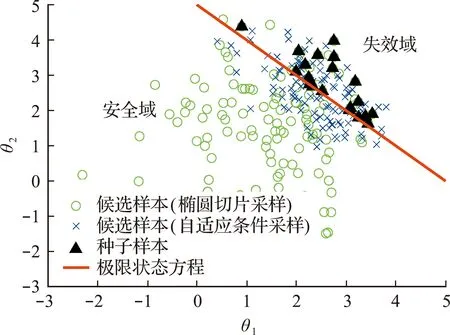
图2 产生步样本分布Fig.2 Sample distribution in Generation step VS aCS sampler

通过分析可知,在可靠度分析领域,椭圆切片采样范围缩减次数的上限与问题维度和失效概率相关。每一次范围的缩减,由于均匀取值的特性,每个维度缩减比例的期望为0.5。若该问题失效区域在每个维度上占比相等,子集模拟最后一层内(所有种子样本皆位于失效区域,所需范围缩减次数最大)采样范围缩减次数的期望可以表示为

log0.5nPf=log0.5Pf/n

(15)

式中n为问题的维度。可以看出,椭圆切片采样的效率随着问题的维度上升而升高(满足上述假定的前提下),但若存在极端情况,即无论问题维度,失效区域的占比始终集中于一维,其余维度采样范围不受目标函数影响,则椭圆切片采样的效率将不随维度变化。

为保证算法效率,在椭圆切片采样中设置范围缩减次数的上限Nmax,以避免目标函数的过多调用。考虑到上述极端情况的存在与结构失效概率的量级,本文设置Nmax=20,其在极端情况下仍能采样到失效区域(Pf≥0.520≈9.54×10-7)内的样本。

3.2 混合采样子集模拟

本文基于上述采样方法提出了一种搭配混合采样器的子集模拟方法。与传统子集模拟始终调用一种采样器不同,该方法在一次模拟内先后调用椭圆切片采样与自适应条件采样两种采样器。如图3所示的示意性算例中,条件失效区域分别标记为A,B和C,随着模拟的三个区域不断缩小

图3 自适应条件采样器和混合采样器Fig.3 aCS sampler VS Mixed sampler

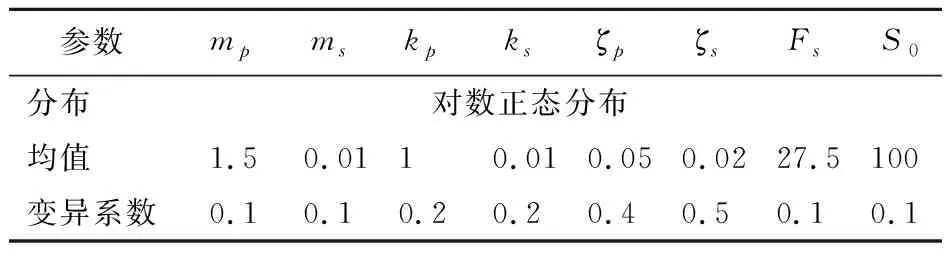
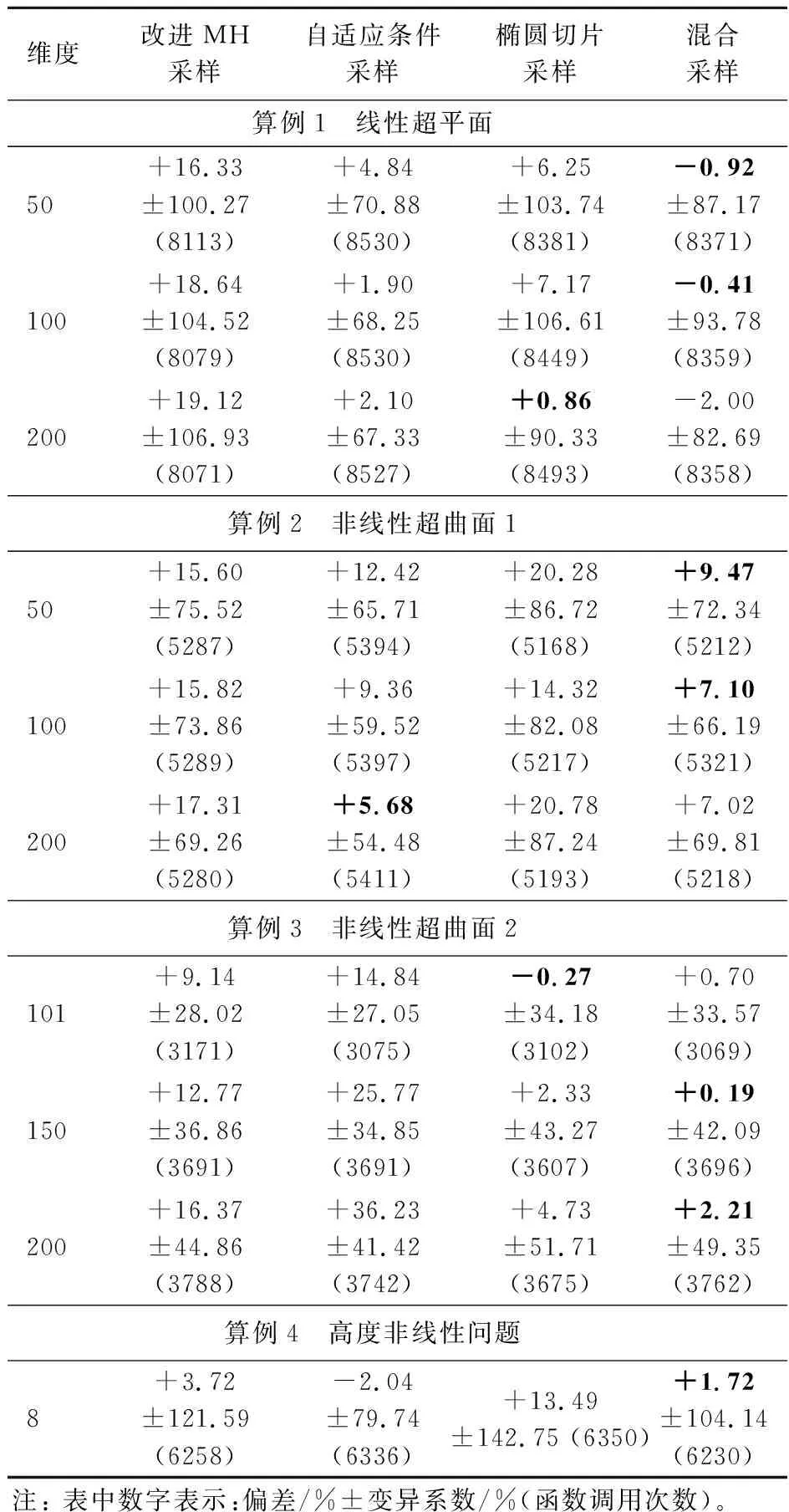
(g(θ)

为避免使用椭圆切片采样器的层数过多导致计算资源浪费,需要设置自适应的采样器切换边界以提升新算法的通用性。本文中当椭圆切片采样器函数调用次数大于样本数的4倍时,判断椭圆切片采样器效率过低,切换为自适应条件采样器。

4 算例分析

援用4个算例(3个可自行控制维度的高维算例以及一个高度非线性算例),从不同角度检验新算法的特性并对比与其他算法的优缺点。

4.1 n维线性超平面[20]

极限状态方程为

(16)

式中Xi(i=1∶n)为独立的标准正态分布变量。该算例中β值控制失效概率的大小,且失效概率不随维度变化,又因为该算例为线性方程,使用FORM可以找到失效概率的解析值,给算法的测试提供了较为便利的环境,可较方便地用来研究算法在不同概率水平和不同维度下的性能。本文取β=6,对应的失效概率Pf=9.87×10-10[20]。

4.2 n维非线性超曲面1[21]

极限状态方程的非线性集中于前两维

(17)

式中Xi(i=1∶n)为独立的标准正态分布变量。k为控制函数非线性的曲率参数,k越大,失效概率越小,对算法要求越大。本文取k=-10,β0=4,对应的失效概率Pf=4.29×10-6[21]。

4.3 n维非线性超曲面2[22]

第二个非线性算例的极限状态方程为以下形式,除第n维外,其他维度皆存在非线性。

(18)

式中Xi(i=1∶n-1)为独立的标准正态分布变量,Xn满足均值为1,标准偏差为0.2的正态分布。与4.1节线性超平面算例不同的是,该算例的失效概率与维度相关且失效概率的值无法通过计算直接得到。因此本文将多次蒙特卡罗积分计算结果的平均值作为失效概率的准确值[22]。

4.4 高度非线性问题[23]

最后一个算例为白噪声激励下具有不确定阻尼振子的双自由度系统,如图4所示,极限状态方程为

图4 白噪声激励下的双自由度系统Fig.4 Two degrees-of-freedom system under white noise excitation

(19)

表1 算例4涉及参数分布Tab.1 Distribution of parameters in example 4

由表2可知,所有算例在各类采样器下运行5000次,保证失效概率浮动基本不影响偏差判断,结果列入表2。对于算例1,除了改进MH采样外,其余算法基本不存在偏差,椭圆切片器由于其采样效率较低,结果的变异系数较大。混合采样器的变异系数位于自适应条件采样与椭圆切片采样之间。在该算例中,所有维度的采样范围都随着模拟层数的增加不断缩减,因此即使该算例对应的失效概率较低,椭圆切片采样仍能取得较好的效果。对于自适应条件采样,该算例的极限状态方程为线性,对于遍历性要求较低,因此也能取得较好的效果。

表2 各算法数值积分结果Tab.1 Results of different MCMC algorithms

算例2中,自适应条件采样的偏差与变异系数都明显好于椭圆切片采样,混合采样偏差与自适应条件采样接近,变异系数位于两者之间,明显优于传统的改进MH采样。在该算例中,极限状态方程的非线性与失效区域的收缩集中在前两个维度,对于自适应条件采样较为有利,而对于椭圆切片采

样的效率不利。在模拟的最后几层中,椭圆切片采样在前两维的采样范围缩减严重,造成样本的大量重复,也导致其模拟结果较差。

对于第三个算例,椭圆切片采样的偏差相较于自适应条件采样更优,变异系数则较大。混合采样偏差与椭圆切片采样接近,变异系数位于两者之间。在该算例中,极限状态方程的非线性与失效区域的收分散于所有维度,对于采样算法的遍历性要求较高,混合采样在保证遍历性的前提下较椭圆切片采样效率更高,因此数值积分结果的变异系数更低。

第四个算例为低维高非线性低失效概率算例,所有采样器除椭圆切片采样外偏差接近,其中自适应条件采样的变异系数最小。该算例说明自适应采样对于低维非线性问题依旧具有良好的遍历性。与算例2类似,椭圆切片采样对此类问题存在样本点难以移动的问题,导致最终模拟结果不理想。混合采样的效果优于椭圆切片采样与传统的改进MH采样。