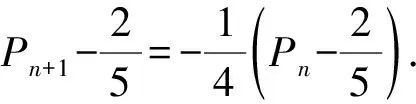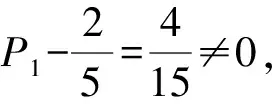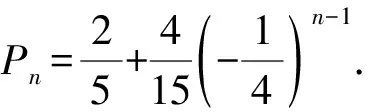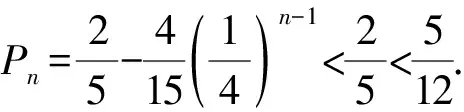全概率公式及其应用

李鸿昌

(北京师范大学贵阳附属中学,贵州 贵阳 550081)

2019年人教A版高中新教材《数学(选择性必修:第三册)》增加了全概率公式的内容,要求结合古典概型,学会用全概率公式计算概率.

全概率公式蕴含的数学思想是:如果某个事件B的概率不易直接计算,那么可以用与事件B有联系的n个两两互斥事件A1,A2,…,An分割事件B,然后利用加法公式和乘法公式求得事件B的概率,这个过程体现了化难为易的转化思想.用简单事件的运算表示复杂事件,利用概率的运算法则简化概率的计算,这种思想方法具有普遍性[1].

1 全概率公式

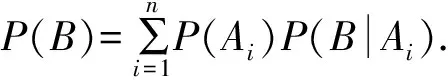
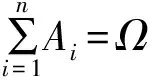
又由条件概率公式,得

即P(Bi)=P(Ai)P(B|Ai).

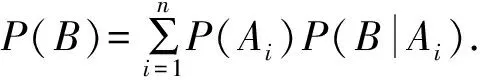
(2)对全概率公式的进一步理解.

①P(Ai)称为先验概率,它反映了各种“原因”发生的可能性大小,一般是以往经验的总结,是试验之前就已知的概率.P(Ai|B)称为后验概率,它反映了试验之后对各种“原因”发生的可能性大小[2].

②全概率公式的思想是“由因推果”,解决的问题是:达到某个目的有多种方式(或造成某种结果有多种原因),问达到目的的概率是多少(或造成这样结果的概率是多少)?

2 全概率公式的应用

全概率公式针对的是某一个过程中已知条件求出最后结果的概率,其解题步骤如下:

找出条件事件里的某一个样本空间——其中的事件分别命名为Ai(i=1,2,…,n)——把目标的概率事件命名为事件B——代入全概率公式求解.

例1 某同学雨伞丢失了.落在图书馆中的概率为50%,这种情况下找回的概率为0.80;落在教室里的概率为30%,这种情况下找回的概率为0.60;落在商场的概率为20%,这种情况下找回的概率为0.05,求找回雨伞的概率.

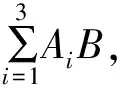
因此由全概率公式,得

例2 (2020年江苏卷)甲口袋中装有2个黑球和1个白球,乙口袋中装有3个白球. 现从甲、乙两个口袋中各任取一个球交换放入另一个口袋,重复n次这样的操作,记甲口袋中黑球个数为Xn,恰有2个黑球的概率为pn,恰有1个黑球的概率为qn.

(1)求p1,q1和p2,q2.

(2)求2pn+qn与2pn-1+qn-1的递推关系和Xn的数学期望E(Xn)(用n表示).

(2)由题意知pn=P(Xn=2),qn=P(Xn=1),1-pn-qn=P(Xn=0).

根据全概率公式可得

整理可得

根据题设式子结构,在上式第一个式子的等号两边同时乘以2并相加可得

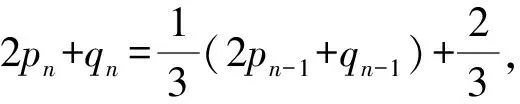
依题意,Xn的取值为0,1,2,其分布列为

Xn012P1-pn-qnqnpn

点评第(1)问是研究初始值并计算第二次操作下的值,也是命题中常见的分步给分的原则.第(2)问不是直接给出递推关系式,而是让考生运用全概率公式来求递推关系式,在递推关系式的处理上借鉴了2019年全国Ⅰ卷21题,给出了研究递推关系式的方向,为期望问题的解决奠定了基础.

例3 甲、乙两人进行射击比赛,每回射击胜者得1分,且每回射击中甲胜的概率为α,乙胜的概率为β(α+β=1),比赛进行到有一人比另一人多2分时则结束,多2分者最终获胜.

(1)试求甲、乙最终获胜的概率;

(2)比赛是否有可能无限地一直进行下去?

解析(1)设A={甲最终获胜},B={乙最终获胜}.以C1记“在第一、二回射击中甲均获胜”,则P(A|C1)=1;以C2记“在第一、二回射击中乙均获胜”,则P(A|C2)=0;以C3记“在第一、二回射击中甲、乙各获胜一次”,则P(A|C3)=P(A).

显然P(C1)=α2,P(C2)=β2,P(C3)=2αβ.

由全概率公式,得

P(A)=P(A|C1)P(C1)+P(A|C2)P(C2)+P(A|C3)P(C3)=α2+0+2αβP(A),

同理,P(B)=P(B|C1)P(C1)+P(B|C2)P(C2)+P(B|C3)P(C3)=β2+0+2αβP(B),

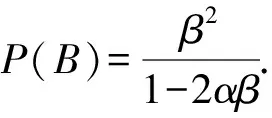
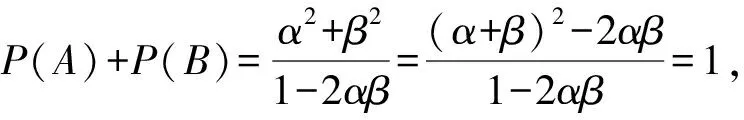
3 变式训练

变式1(多选题)甲罐中有5个红球、2个白球和3个黑球,乙罐中有4个红球、3个白球和3个黑球.先从甲罐中随机取出一球放入乙罐,分别以A1,A2和A3表示甲罐取出的球是红球、白球和黑球的事件;再从乙罐中随机取出一球,以B表示由乙罐取出的球是红球的事件,则下列结论中正确的是( ).

C.事件B与事件A1相互独立

D.A1,A2,A3是两两互斥的事件

综上,正确的选项是BD.

变式2 某保险公司将其公司的被保险人分为三类:“谨慎的”“一般的”“冒失的”.统计资料表明,这三类人在一年内发生事故的概率依次为0.05,0.15,0.30.若该保险公司的被保险人中“谨慎的”被保险人占20%,“一般的”被保险人占50%,“冒失的”被保险人占30%,则该保险公司的一个被保险人在一年内发生事故的概率是( ).

A.0.155 B.0.175 C.0.016 D.0.096

解析设事件B1表示被保险人是“谨慎的”,事件B2表示被保险人是“一般的”,事件B3表示被保险人是“冒失的”,则P(B1)=20%,P(B2)=50%,P(B3)=30%.

变式3 李明早上上学的时候,可以乘坐公共汽车,也可以乘坐地铁.已知李明乘坐公共汽车的概率为0.3,乘坐地铁的概率为0.7.而且乘坐公共汽车与地铁时,李明迟到的概率分别为0.2与0.05.

(1)求李明上学迟到的概率;

(2)如果某天早上李明上学迟到了,那么他乘公交车的概率为多少?

解析(1)记小明乘坐公共汽车为事件A,乘坐地铁为事件B,迟到为事件C,根据题意得P(A)=0.3,P(B)=0.7,P(C|A)=0.2,P(C|B)=0.05,由全概率公式得

P(C)=P(AC)+P(BC)=P(C|A)P(A)+P(C|B)P(B)=0.2×0.3+0.05×0.7=0.095.

(2)由条件概率公式得

变式4 为了避免就餐聚集和减少排队时间,某校开学后,食堂从开学第一天起,每餐只推出即点即取的米饭套餐和面食套餐.已知某同学每天中午会在食堂提供的两种套餐中选择,已知他第一天选择米饭套餐的概率为2/3,而前一天选择了米饭套餐后一天继续选择米饭套餐的概率为1/4,前一天选择面食套餐后一天继续选择面食套餐的概率为1/2,如此往复.

(1)求该同学第二天中午选择米饭套餐的概率;

(2)记该同学第n天选择米饭套餐的概率为Pn.

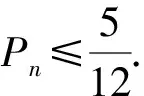
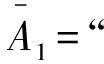
由全概率公式,得

Pn+1=P(An+1)