关于解决高中数学中最值问题的分析
2023-10-26苗祥磊王德朋
苗祥磊 王德朋
(1.喀什第二中学,新疆 喀什 844099;2.喀什大学数学与统计学院,新疆 喀什 844008)
最值问题是高中数学中比较常见的题目,亦是高考中经常考查的题目.针对该问题的解题方法也比较灵活、多样,不同的题型,分析解决问题的方法也不一样.运用函数思想与数形结合思想对于求解这类问题都有着极强的助力.
1 函数中的最值问题
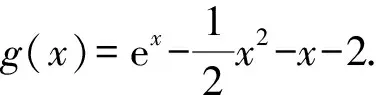
(1)求函数g(x)在[-1,+∞)上的最小值;

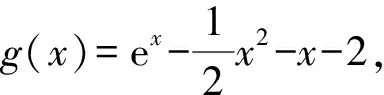

表1 函数的单调性
因此当x=-1时,g(x)取得最小值,即



2 三角函数中的最值问题

(1)把f(x)的解析式改写为f(x)=Asin(ωx+φ)(A>0,ω>0)的形式;

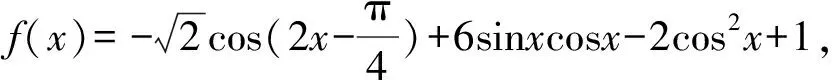
整理,得f(x)=2sin2x-2cos2x
(2)结合第(1)问,f(x)的最小正周期为
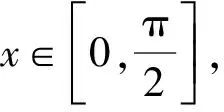


3 数列中的最值问题

(1)求数列{an},{bn}的通项公式;




又因为Tn=a1·2n+2-4=2n+2-4,
所以b1=T1=4,bn=Tn-Tn-1=2n+2-4-(2n+1-4)=2n+1.
Sn=2×2+3×22+4×23+…+(n+1)·2n,
2Sn=2×22+3×23+…+(n+1)·2n+1,

所以Sn=n·2n+1.




综上,k的取值范围为(2,+∞).
4 解三角形中的最值问题

解析根据b2+c2=accosC+c2cosA+a2,由余弦定理,得
①

②

③




5 平面向量中的最值问题

(1)求实数λ的值;



“一生四梦,得意处惟在牡丹”[1]的《牡丹亭还魂记》,主要依据《杜丽娘慕色还魂》改编,这是不争的事实。但魏晋志怪、唐人传奇对《牡丹亭》创作的影响,人们常常估计不足。汤显祖在《牡丹亭题词》里明明白白写道:

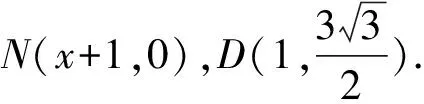
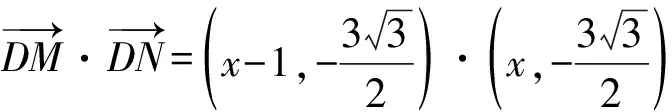
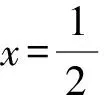
6 圆锥曲线中的最值问题
例6已知F为抛物线C:y2=4x的焦点,过点F作两条互相垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,求|AB|+4|DE|的最小值.
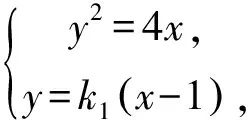
设A(x1,y1),B(x2,y2),由韦达定理,得



综上,|AB|+4|DE|的最小值为36.
高中数学中大部分内容都能与函数的最值问题联系起来[1],也是考题中经常出现的题目,难度较大,方法也比较灵活.教师在教学中要把最值问题作为一个专题,引导学生掌握解题方法,做到具体问题具体分析,引导学生对每一种类型题都能够有思路,锻炼学生的思维能力.总之,思路要灵活,掌握解题方法是最关键的.
