2023年新高考Ⅰ卷第22题解法探究
2023-10-26叶诚理林品玲
数理化解题研究 2023年28期
叶诚理 林品玲
(福建省福清第一中学,福建 福清 350300)
解析几何一直就是高考试卷的主干知识,2023年新高考Ⅰ卷就把解析几何中的抛物线作为压轴题考查,给人耳目一新的感觉.
1 试题呈现

(1)求W的方程;

本题以抛物线中的内接直角三角形为载体,考查了抛物线的方程、性质和弦长计算,考查数形结合、化归转化、函数方程等思想,考查数学抽象、逻辑推理、直观想象、数学运算等核心素养,体现基础性、综合性和创新性.
本题的命题背景源于教材(新人教A版选择性必修一P46页章末第10题)、往年数学竞赛(上海1998年高中数学竞赛试题第12题)和高考题(2017年高考数学新课标Ⅰ卷理科第10题).
2 解法探析
2.1 第(1)问解析
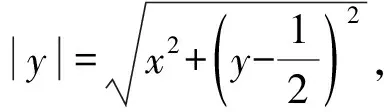
2.2 第(2)问解析
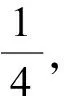

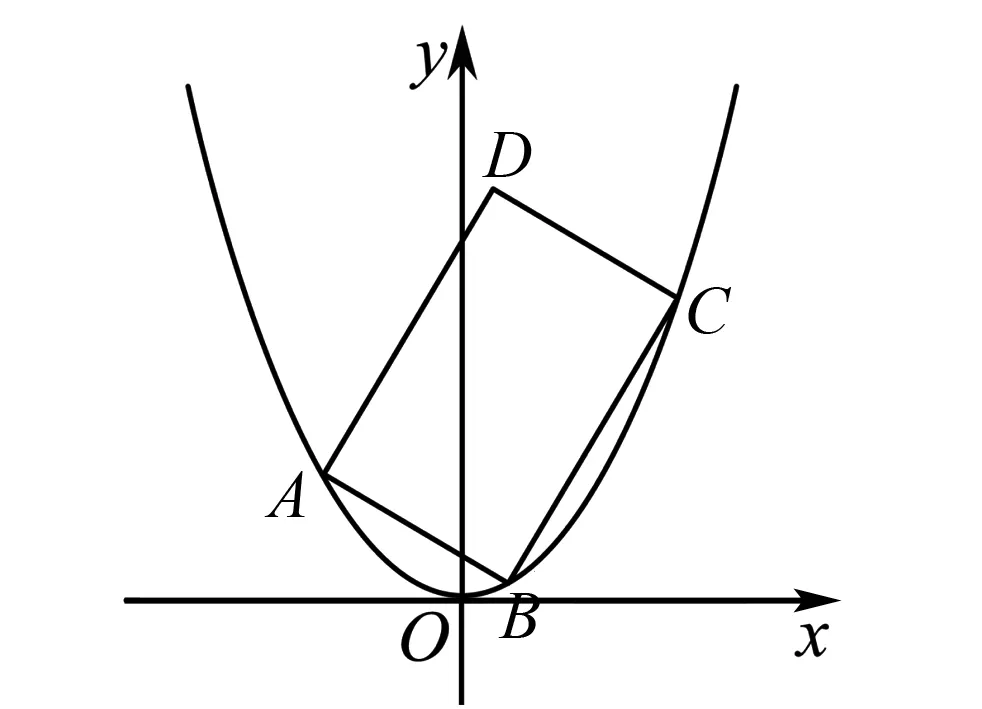
图1 解法1示意图
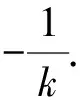
x2-kx+ka-a2=0.
则xA·xB=a·xA=ka-a2.即xA=k-a.



令k2=m,则m∈(0,1].
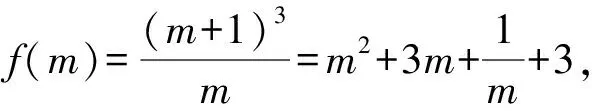




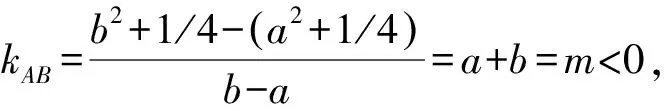



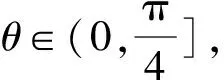

图2 解法3示意图
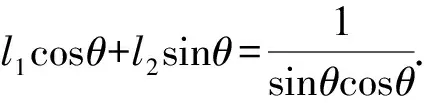
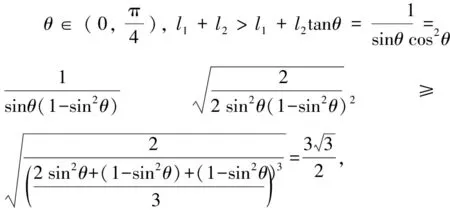



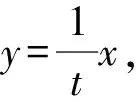

图3 解法4示意图
2.3 试题推广
事实上,对于一般的抛物线W:x2=2py(p>0),已知矩形ABCD有三个顶点在W上,则有

推论2若四边形ABCD为正方形,则面积的最小值为2p2;
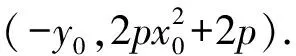
3 策略剖析
上述几种解法的解题过程充分体现了依托几何直观,合理运算求解的解题策略.以解法1为例,见表1.

表1 策略剖析表
另外,掌握代数运算的技巧也是必不可少的,凸显解析几何的本质:用代数的方法来研究几何问题. 体现在如下几点:

因此,要想顺利解决本题,需要学生掌握扎实的数学基础知识,学会在复杂情境中懂得灵活地、综合地运用所学知识分析问题、解决问题的能力,即充分挖掘几何特征,实现巧妙转化和创造性地求解,问题的解决过程充分考查了学生的直观想象、抽象概括、逻辑推理、数学运算核心素养和良好的心理素质,体现了命题者的意图.
