一道求双变量最小值问题的多视角探究
2023-10-26李春林
李春林
(甘肃省天水市第九中学,甘肃 天水 741020)
在双变量或多变量约束条件下,求代数式的最值问题是近几年高考、强基计划、高中数学联赛等考试中常见的一类题目.此类问题往往情境新颖,双变量关系呈现多样化特点.破解此类题的关键是结合双变量代数式的基本特征,合理恒等变形,巧妙运算转化,通过从不等式、函数、方程、三角函数、平面向量、导数等视角入手,进行分析探究[1].
1 试题呈现
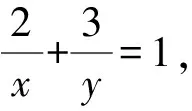
2 多视角探究
视角1 先数式代换,再利用基本不等式
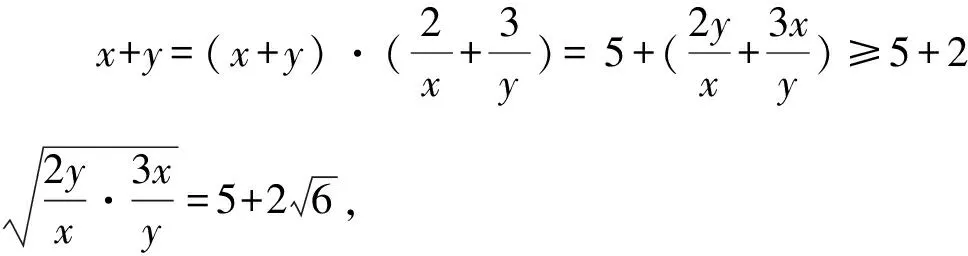

点评利用逆向思维进行数式代换,从形式上将问题转化为能利用基本不等式的结构,从而将问题解决.“1”的逆代换是解题的关键一环.
视角2将分式条件适当变形化为整式,再利用基本不等式
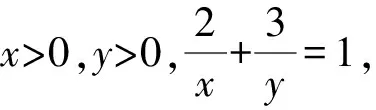
所以xy-3x-2y=0(x>2,y>3).
所以xy-3x-2y+6=6.
即(x-2)·(y-3)=6.


点评分式化整式后,巧妙构造乘积为定值,结合基本不等式,问题得解.
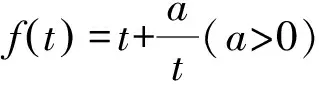
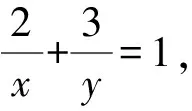





点评将式中的y用x表示,从而将该问题转化为函数问题.利用对勾函数的性质,即得结果.当然也可以用导数或基本不等式求得最小值[2].
视角4利用柯西不等式

点评将代数式适当变换,即可构造出适合柯西不等式的条件,从而迅速得解.
视角5引入参数t,令t=x+y,代入已知中得关于x的一元二次方程.由于该方程的两实根都大于2,故由一元二次方程实根分布得解.
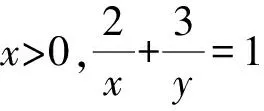
①
因为该方程的实根都大于2,
所以令f(x)=x2+(1-t)x+2t,则有

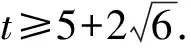

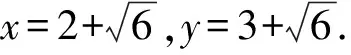
点评引入参数t,“二元”化“一元”,将问题转化为含t的一元二次方程的实根分布问题得以解决[3].
视角6利用三角函数代换求值.
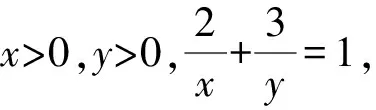
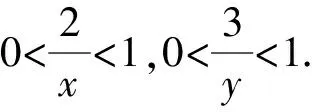


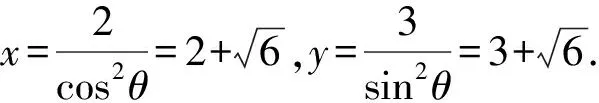
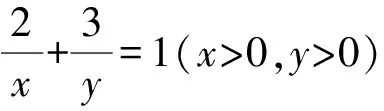
视角7根据平面向量的性质:a=(x1,y1),b=(x2,y2),a·b≤|a|·|b|,当且仅当x1=λx2,y1=λy2(λ>0)时,等号成立.
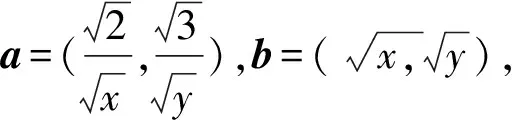
因为a·b≤|a|·|b|,
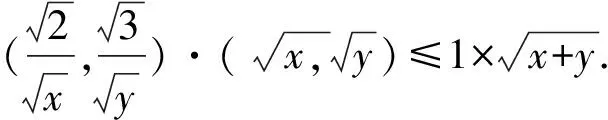

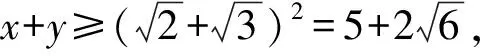
点评巧妙构造向量a,b,由a·b≤|a|·|b|,迅速得解.恰当构造平面向量a,b是解题的关键.
视角8利用函数的图象,数形结合求解.


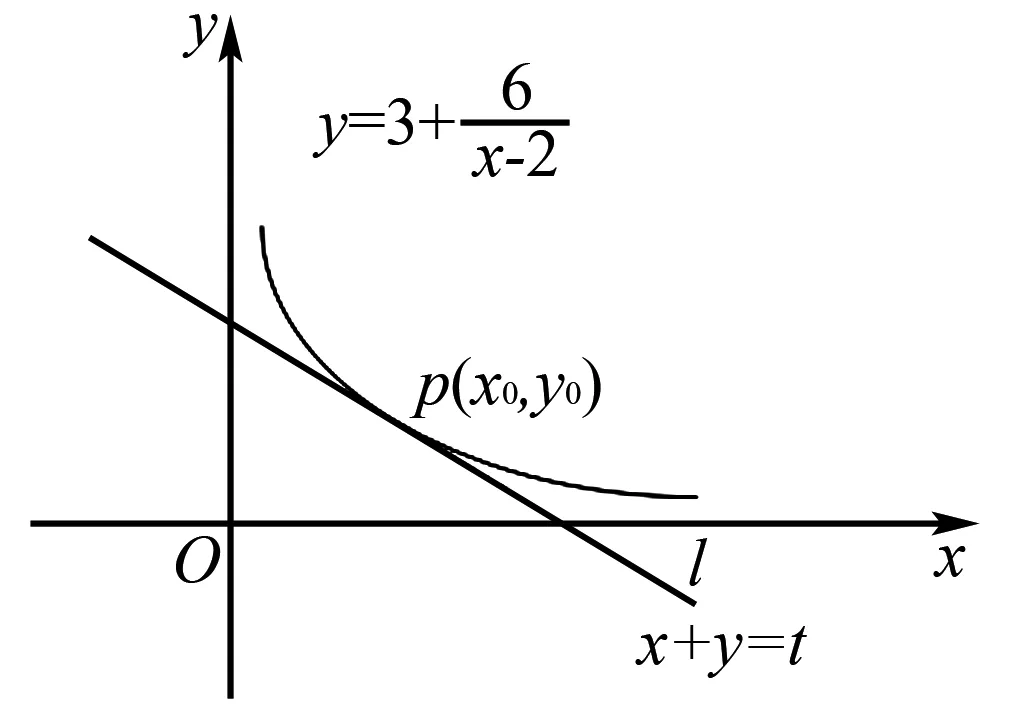
图1 解法8示意图
点评探究代数问题的图形背景,利用其几何图形的性质,以形助数,数形结合,从而获得直观、简洁的解法.
3 解后反思
双变量最值问题是近几年高考数学复习中出现频率较高的一类题目,难度较大.而且此类试题在持续地变化与创新中,难度有增大的趋势,针对本题笔者从不等式、函数、方程、三角函数、平面向量、导数等视角入手,进行分析探究.从上述解法中可以看到,求解特定代数关系背景下的双变量最值问题,必须结合双变量代数式的基本特征,认真分析,细心观察,善于联想,多角度思考,合理整合,巧妙应用,准确推理运算.探索解题途径时,需举一反三,灵活变通,将数学知识、数学能力、数学思维有机融合,有效应用于解题.在解题的过程中,要不断总结解题的规律,剖析解法的本质,引导一题多解走向深入,从而形成良好的数学解题品质,提升数学核心素养.
