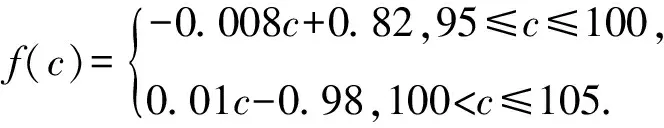核心素养角度解读2023年数学高考Ⅰ卷

何正文

(广东省肇庆市百花中学,广东 肇庆 526000)

2023年新高考卷,考生普遍反映比去年简单,和往年高考Ⅰ卷相比,更加充分发挥基础学科的作用,突出素养和能力考查,重视思维品质,体现思维过程,关注思维能力.今年试题重视基础性,注重综合性,强调应用性和突出创新性,加大了对学科素养和关键能力的考查力度.本文对2023年高考卷的试题进行剖析,从数学抽象、逻辑推理、数学建模、数学运算、直观想象和数据分析六个方面进行解读.

1 数学抽象

2023年高考题,在数学抽象问题方面,设置合理的思维强度和抽象程度,注重打破函数和几何联系,把一些背景性的问题抽象成我们熟悉的数学问题,进而进行求解.

例1 (2023年新课标Ⅰ卷多选题第11题)已知函数f(x)的定义域为R,f(xy)=y2f(x)+x2f(y),则( ).

A.f(0)=0 B.f(1)=0

C.f(x)是偶函数 D.x=0为f(x)的极小值点

解析因为f(xy)=y2f(x)+x2f(y),

对于A,令x=y=0,得f(0)=0×f(0)+0×f(0)=0,故A正确.

对于B,令x=y=1,得f(1)=1×f(1)+1×f(1),则f(1)=0,故B正确.

对于C,令x=y=-1,得f(1)=f(-1)+f(-1)=2f(-1),则f(-1)=0,

令y=-1,得f(-x)=f(x)+x2f(-1)=f(x).

又函数f(x)的定义域为R,所以f(x)为偶函数,故C正确,

对于D,不妨令f(x)=0,显然符合题设条件,此时f(x)无极值,故D错误.

故选ABC.

解析记AB=c,AC=b,BC=a,

由余弦定理,得

22+b2-2×2×b×cos60°=6.

由S△ABC=S△ABD+S△ACD,得

故答案为2.

2 逻辑推理

2023年高考题在逻辑推理考查上突出对问题的总结与分析,注重打破函数和几何联系,要求考生根据题意推理讨论,考查考生思维的条理性、严谨性.

A.bc>0 B.ab>0 C.b2+8ac>0 D.ac<0

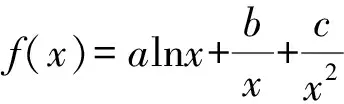
因为函数f(x)既有极大值也有极小值,则函数f′(x)在(0,+∞)上有两个变号零点,而a≠0,因此方程ax2-bx-2c=0有两个不等的正根x1,x2.

即有b2+8ac>0,ab>0,ac<0,显然a2bc<0,即bc<0,A错误,BCD正确.

评注本题考查本质是根据一元二次方程根的性质判定方程系数之间的关系,由于函数既有极大值又有极小值,所以转化为一元二次方程的两个正根问题,所以求出函数f(x)的导数f′(x),由已知可得f′(x)在(0,+∞)上有两个变号零点,转化为一元二次方程有两个不等的正根.

A.甲是乙的充分条件但不是必要条件

B.甲是乙的必要条件但不是充分条件

C.甲是乙的充要条件

D.甲既不是乙的充分条件也不是乙的必要条件

则Sn=nan+1-t·n(n+1).

有Sn-1=(n-1)an-t·n(n-1),n≥2.

两式相减,得an=nan+1-(n-1)an-2tn.

即an+1-an=2t,对n=1也成立.

因此{an}为等差数列,则甲是乙的必要条件,

所以甲是乙的充要条件,C正确.

评注本题以等差数列为材料考查充要条件的推证,要求考生判别充分性和必要性,然后分别进行证明,解决问题的关键是利用等差数列的概念和特点进行推理论证.利用充分条件、必要条件的定义及等差数列的定义,再结合数列前n项和与第n项的关系推理判断作答.

3 数学建模

数学建模作为核心素养的关键部分,在处理实际问题时往往可以做到事半功倍.如果能把问题进行模型化,数据就可以可视化,图形就可以立体化[1].

解析因为a+b+c=0,所以a+b=-c.

即a2+b2+2a·b=c2.

即1+1+2a·b=2.

所以a·b=0.

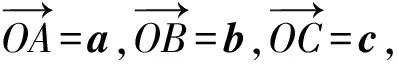
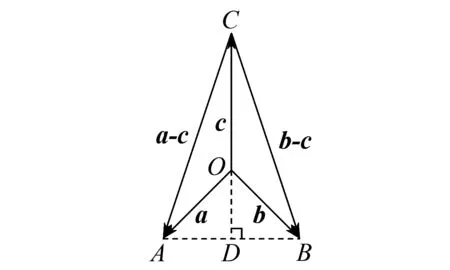
图1 例5解析图

cos〈a-c,b-c〉=cos∠ACB=cos2∠ACD

=2cos2∠ACD-1

故选D.

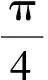
故选C.

图2 例6解析图

4 数学运算

2023年的试题要求考生理解运算对象,掌握运算法则,探究运算思路,求得运算结果.数学运算需要学生充分理解题目,把握题目考查的内容.需要学生养成独立思考和深入思考的习惯,发展思维的全面性与深刻性[2].

例7(2023年新课标Ⅰ卷第17题)已知在△ABC中,A+B=3C,2sin(A-C)=sinB.

(1)求sinA;

(2)设AB=5,求AB边上的高.

解析(1)因为A+B=3C,

又2sin(A-C)=sinB=sin(A+C),

则2sinAcosC-2cosAsinC=sinAcosC+cosAsinC.

所以sinAcosC=3cosAsinC.

所以sinA=3cosA.

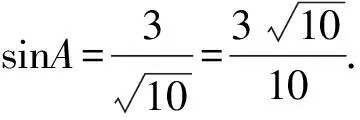
由sinB=sin(A+C)=sinAcosC+cosAsinC

评注本题涉及正弦定理、同角三角函数基本关系式、解三角形等数学内容,考查数学运算素养.

(1)根据角的关系及两角和差正弦公式,化简即可得解;

(2)利用同角之间的三角函数基本关系及两角和的正弦公式求sinB,再由正弦定理求出b,根据等面积法求解即可.

A.p=2

C.以MN为直径的圆与l相切

D.△OMN为等腰三角形

B选项:设M(x1,y1),N(x2,y2),

3x2-10x+3=(x-3)(3x-1)=0.

C选项:如图3,设MN的中点为A,M,N,点A到直线l的距离分别为d1,d2,d,

D选项:由上述分析可知

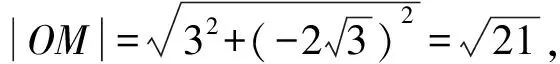
所以△OMN不是等腰三角形,故D选项错误.

故选AC.

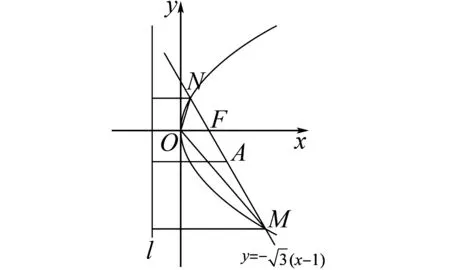
图3 例8解析图

评注本题设置直线与抛物线相交的情境,通过直线方程与抛物线方程的联立考查计算能力.先求得焦点坐标,从而求得p,根据弦长公式求得|MN|,根据圆与等腰三角形的知识确定正确答案.

5 直观想象

直观想象是指通过直观几何和想象空间形式,利用几何图形分析解决问题,也就是通过把题目想象成一个实物,以几何体为依托,发现空间线面关系.

例9(2023年新课标Ⅱ卷多选题第9题)已知圆锥的顶点为P,底面圆心为O,AB为底面直径,∠APB=120°,PA=2,点C在底面圆周上,且二面角P-AC-O为45°,则( ).

A.该圆锥的体积为π

解析依题意,∠APB=120°,PA=2,

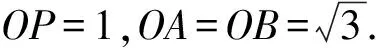
故选AC.

图4 例9解析图

评注本题以多选题的形式考查圆锥的内容,根据圆锥的体积、侧面积判断A,B选项的正确性,利用二面角的知识判断C,D选项的正确性.4个选项设问逐次递进,前面选项为后面选项提供条件,各选项分别考查圆锥的不同性质,互相联系,重点突出.

例10(2023年全国甲卷理科第15题)在正方体ABCD-A1B1C1D1中,E,F分别为CD,A1B1的中点,则以EF为直径的球面与正方体每条棱的交点总数为____.

解析不妨设正方体棱长为2,EF中点为O,取AB,BB1中点G,M,侧面BB1C1C的中心为N,连接FG,EG,OM,ON,MN,如图5.

图5 例10解析图

同理,根据正方体的对称性知,其余各棱和球面也只有1个交点,

所以以EF为直径的球面与正方体每条棱的交点总数为12.

6 数据分析

2023年的数据分析题在命制情境化试题过程中,在剪裁素材方面,注意控制文字数量和阅读理解难度,使情境化试题能够引导考生树立理想信念,热爱科学,达到试题要求层次与考生认知水平的契合与贴切[3].

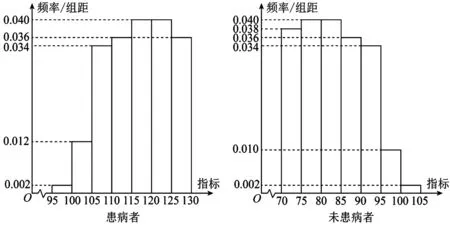
图6 患病者与未患病者医学指标频率分布直方图

例11(2023年新课标Ⅱ卷第19题)某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异,经过大量调查,得到如图6的患病者和未患病者该指标的频率分布直方图,利用该指标制定一个检测标准,需要确定临界值c,将该指标大于c的人判定为阳性,小于或等于c的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率,记为p(c);误诊率是将未患病者判定为阳性的概率,记为q(c).假设数据在组内均匀分布,以事件发生的频率作为相应事件发生的概率.

(1)当漏诊率p(c)=0.5%时,求临界值c和误诊率q(c);

(2)设函数f(c)=p(c)+q(c),当c∈[95,105]时,求f(c)的解析式,并求f(c)在区间[95,105]的最小值.

解析(1)依题可知,左边图形第一个小矩形的面积为5×0.002>0.5%,所以95

所以(c-95)×0.002=0.5%,解得c=97.5.

所以q(c)=0.01×(97.5-95)+5×0.002=0.035=3.5%.

(2)当c∈[95,100]时,

f(c)=p(c)+q(c)=(c-95)×0.002+(100-c)×0.01+5×0.002=-0.008c+0.82≥0.02;

当c∈(100,105]时,

f(c)=p(c)+q(c)=5×0.002+(c-100)×0.012+(105-c)×0.002=0.01c-0.98>0.02.

所以f(c)在区间[95,105]的最小值为0.02.

评注本题要求合理平衡漏诊率和误诊率,制定检测标准,试题情境既有现实意义,又体现数学学科的应用价值

(1)根据题意由第一个图可先求出c,再根据第二个图求出c≥97.5的矩形面积即可解出;

(2)根据题意确定分段点100,即可得出f(c)的解析式,再根据分段函数的最值求法即可解出.

总体来说,2023年的题目严格依据高中课程标准,深化基础性和综合性,聚焦学科核心素养,精选试题情境,加强关键能力考查,促进学生提升科学素养,引导全面发展,助推高中育人方式改革,继续突出反套路、反机械刷题特点,突出强调对基础知识和基本概念的深入理解和灵活掌握,注重考查学科知识的综合应用能力,重视思维培养,同时,合理控制试题难度,进一步培养学生的数学核心素养.