矩量法研究分层粗糙面与运动圆形截面柱的复合电磁散射

于少帅,任新成,杨天赐,朱小敏,赵 晔

(延安大学 物理与电子信息学院,陕西延安 716000)

地物背景与运动目标的复合电磁散射特性可为目标的雷达成像、识别、检测及分类等提供一定的理论依据,用于对地物表面运动车辆、海洋表面上方低空飞行物的监测等[1-4]。由于自然界中地海背景的复杂性,分层粗糙面的电磁散射具有更加重要的应用价值,实际的分层粗糙面包括沥青路面、被雪覆盖的地面及草原表面等,沙地由于湿度不同,海水由于温度、含盐量不同,也可视作分层粗糙面进行研究。在地海表面与目标复合电磁散射研究中,目标的运动状态一般都是静止的,在任何方向上都不会发生位移。之前的研究中,Behdani等[5]使用物理光学方法研究了海面与2维船体目标的复合电磁散射,董子宇等[6]使用时域有限差分法(finite difference time domain,FDTD)研究了沥青混凝土地面的电磁散射特性,田炜等[7]使用矩量法(method of moments,MOM)研究了雪层覆盖地面的电磁散射特性,王赵隆等[8]提出了一种计算多粗糙度分层粗糙面及上方目标的新型算法,分析了粗糙度及各层粗糙面之间的间距等对复合电磁散射系数的影响,张连波等[9]应用矩量法研究了3层粗糙面的复合散射特性,分析了多层与单层粗糙面电磁散射特性的异同。

以上研究中,粗糙面上方的散射目标均处于静态,即不考虑目标位移对复合散射特性的影响,所以国内外学者通常研究的是目标和粗糙面的各种本征参数对散射系数的影响。然而在自然界中,散射目标大多是运动的,而目标的运动会一定程度上影响目标本身的散射特性及粗糙面和目标之间的耦合,从而对目标与粗糙面的复合散射特性产生一定影响。

1 复合散射建模

图1为分层粗糙面与上方运动目标的复合散射模型。其中,目标所在的上方空间为自由空间,记为V0;下方为两层独立的均匀媒质V1,V2;εs1和εs2分别为V1与V2的介电常数;ki为入射波波矢;ks为散射波波矢;θi和θs分别为入射角和散射角;目标轮廓函数记为yt(x),a、b分别为该目标重心G到x轴、y轴的距离;c为该目标重心G到坐标轴原点O的距离;无任何特殊说明下,令上方运动目标与粗糙面相接,即令a=2.0λ;两层粗糙面的轮廓函数分别记为f1(x),f2(x),且深度分别为d1,d2,d2=d1-d,d为两粗糙面在竖直方向的距离,无任何特殊说明的情况下,d1取0。

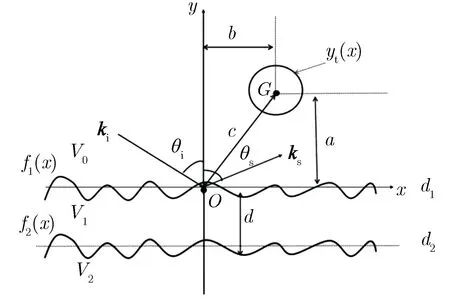
图1 分层粗糙面与上方运动目标的复合散射模型Fig.1 Composite scattering model of layered rough surface and moving target above

1.1 分层粗糙面建模

本文使用蒙特卡罗方法生成分层粗糙面,根据蒙特卡罗方法,得出粗糙面功率谱后可由函数生成长度为L的1维粗糙面。表示为[10]

(1)

其中:xn=nΔx(n=-N/2,...,N/2)为粗糙面的第n个采样点;F(kj)为滤波后所得到的粗糙面频谱;f(xn)为F(kj)的傅里叶变换对。F(kj)可表示为

(2)

其中:kj=2πj/L;Δk为谱域相邻的谐波样本的空间波束差;S(kj)为粗糙面的功率谱密度,用S1(kj)和S2(kj)分别表示第一层和第二层粗糙面的功率谱密度;N(0,1)表示均值为0,方差为1的正态分布随机数。当j>0时,F(kj)满足共轭对称关系F(kj)=F(k-j)*。

常用的粗糙面功率谱密度有高斯粗糙面和指数粗糙面等,本文在建模分层土壤表面时,两层粗糙土壤表面均选用指数功率谱密度来模拟,表示为

(3)

其中:k为波数;δ和l分别为质素和粗糙面的均方根高度和相关长度。得到指数功率谱密度之后,利用式(1)和式(2)即可模拟生成1维指数随机粗糙面。

1.2 土壤介电常数模型

对于土壤而言,土壤本身的湿度对介电常数具有决定性影响,Topp模型因简洁性和有效性应用较为广泛,忽略了多种土壤的本征参数对介电常数所产生的影响,认为土壤的介电常数仅与湿度成一定关系,表示为

(4)

其中:mv为土壤湿度;εs为土壤介电常数。本文选取该模型模拟分层土壤表面中V1,V2区域的介电常数。

1.2.2 核密度估计法(KDE) 核密度估计法(KDE)是基于密度的空间点模式分析方法中应用最为广泛的一种非参数估计方法.核密度方程的几何意义为：密度分布在每个xi点中心处最高，向外不断降低，当距离中心达到一定阈值范围(窗口的边缘)处密度为0.运用该原理对每一个样本点进行计算，将相同位置处的密度进行叠加，得到点要素在整个区域的分布密度[24].网格中心处的核密度为窗口范围内的密度和：

1.3 复合系数

为减小边缘效应所造成的人工反射,引入锥形波[13]作为入射波,此时粗糙面与目标的复合散射系数可表示为[10]

(5)

其中:k0为空间波数;g为锥形因子;ψsN(θs,θi)为散射波。在计算过程中,取归一化复合散射系数[14]σ=lgσ(θs)。

2 数值计算结果与讨论

为验证MOM的正确性,在分层粗糙面参数和电磁波入射角大小等参数完全相同的条件下,使用MOM与FDTD[15]对分层粗糙面及其上方圆形截面柱的复合散射系数进行计算,计算结果如图2所示。

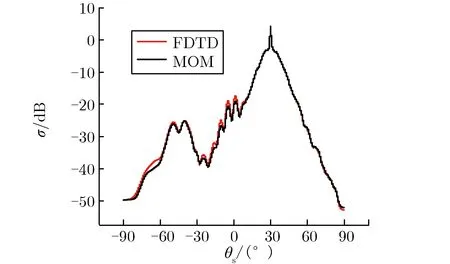
图2 MOM与FDTD数值计算结果Fig.2 Comparison of numerical calculation resultsbetween MOM and FDTD

由图2可见,两种算法所得出的角分布曲线吻合得非常好,证明了本文所用MOM的正确性。

在本文仿真中,如无特殊说明,入射电磁波频率均为1 GHz,入射角θi=30°,归一化尺度参数σ1h=σ2h=0.1λ,互相关长度l1=l2=3λ,粗糙面间距为15λ,介电常数εs1=4.94,εs2=18.22,圆形截面柱目标半径为2λ,重心G到x轴的距离a=2λ(即与地面接触)、到y轴的距离b=0,粗糙面仿真统计个数为100。

2.1 纵向平移对散射系数的影响

保持其他变量不发生任何变化,取目标重心G到x轴的距离a分别为2λ,30λ,60λ,计算目标纵向平移的距离对复合散射系数σ的影响,目标纵向平移距离不同时,散射系数随散射角的变化关系如图3所示。由图3可见,目标的纵向平移距离a对复合散射系数σ有着比较规律的影响,当-90°<θs<10°时,a越大,σ越小,而当10°<θs<60°时,散射系数几乎不随a的变化而变化,当60°<θs<90°时,a越大,σ越小。

复合散射系数受目标纵向平移距离a的影响较为明显,这是因为目标在纵向移动的过程中,虽然目标自身的散射特性变化非常小,但目标与粗糙面之间的耦合散射特性受到的影响较大,进而影响到复合散射场。因此,目标纵向平移时,散射系数会受到较显著的影响。

图3 目标纵向平移距离不同时,散射系数随散射角的变化关系Fig.3 σ vs. θs with different a

2.2横向平移对散射系数的影响(接触地面)

分别取目标重心G到y轴的距离为0,30λ,45λ,并取a=2λ(即与粗糙面接触),保持其他条件不变,分析计算目标在水平方向移动距离b对散射系数σ产生的影响。接触地面,目标在水平方向移动距离不同时,散射系数随散射角的变化关系如图4所示。

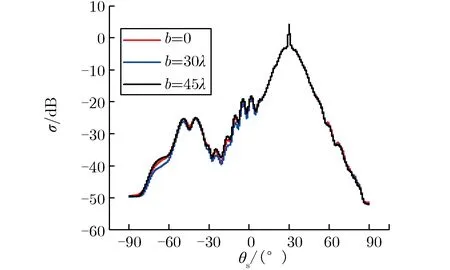
图4 接触地面,目标在水平方向移动距离不同时,散射系数随散射角的变化关系Fig.4 σ vs. θs with different b when touching the ground

由图4可见,复合散射系数σ随散射角θs振荡地变化,在镜反射方向(θs=30°)时达到最大。从总体上来看,目标横向平移的距离b对复合散射系数σ的影响并不显著,尤其是在镜反射方向附近的范围,即当0<θs<60°时,σ几乎没有任何变化,在散射角θs的其他范围,b=45λ时的σ最大,b=0次之,b=30λ的σ最小。但目标横向移动时σ的变化非常小,这是因为目标在横向平移时,目标自身及目标与粗糙面间耦合的散射特性变化都非常小,所以分层粗糙面上方目标在水平方向移动时,复合散射系数受到的影响也非常小。

2.3横向平移对散射系数的影响(不接触地面)

分别取目标重心G到y轴的距离b=0,30λ,45λ,并取a=10λ(即目标漂浮在粗糙面上方),保持其他条件不变化,计算不接触地面,目标在水平方向移动距离不同时,散射系数随散射角的变化关系,如图5所示。由图5可见,当目标漂浮在粗糙面上方时,复合散射系数σ受到目标在水平方向的移动距离b的影响依然不是很显著,但与目标和粗糙面接触的情形相比,σ受到b的影响更加规律且更加明显,当θs<0时,总有b越大,σ越小;θs>0时,即在镜反射方向(θs=30°)附近时,复合散射系数σ几乎不随b的变化而变化。

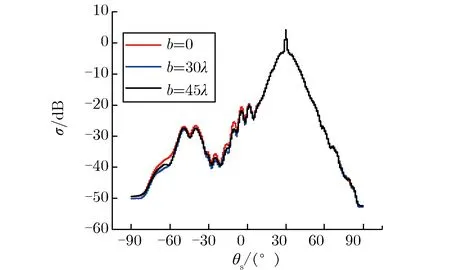
图5 不接触地面,目标在水平方向移动距离不同时,散射系数随散射角的变化关系Fig.5 σ vs. θs with different b without touching the ground

与散射目标接触粗糙面的情形类似,目标横向移动时,σ的变化非常小,这同样是因为目标在横向平移时,目标自身及目标与粗糙面间耦合的散射特性变化都非常小,所以分层粗糙面上方漂浮目标在水平方向移动时,复合散射系数受到的影响也非常小。

2.4 斜向平移对散射系数的影响

分别取目标重心G到坐标轴原点O的距离c=2λ,22λ,44λ,且令目标重心G到y轴的距离b与到x轴的距离a相等,即令线段OG与x轴的夹角始终为45°,保持其他条件不变,分析计算目标沿OG方向移动距离c不同时,散射系数随散射角的变化关系,如图6所示。

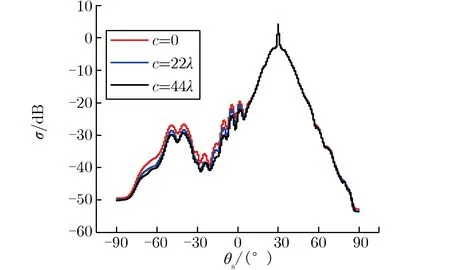
图6 目标延OG方向移动距离不同时,散射系数随散射角的变化关系Fig.6 σ vs. θs with different c

由图6可见:当15°<θs<85°时,散射系数σ几乎不随c的变化而变化;当θs在其他范围内变化时,c对σ的影响则较为明显;当-90°<θs<15°或θs>85°时,总有c越大,σ越小的规律。这一现象表明,目标斜向平移的距离c也会对复合散射系数σ造成较大的影响,因为目标的斜向平移也会一定程度影响目标与土壤表面的耦合,从而影响复合散射系数,所以土壤表面上方目标进行斜向移动,会对复合散射系数造成较直观的影响。

2.5 电磁波入射角对散射系数的影响

分别取入射角θi为30°,45°,60°,保持其他条件不变,分析计算电磁波入射角θi不同时,散射系数σ随散射角的变化关系如图7所示。

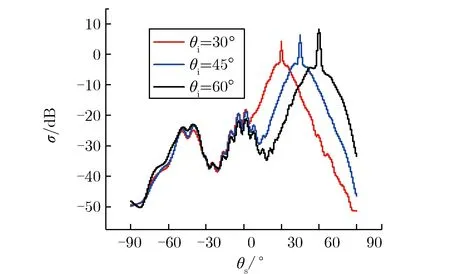
图7 电磁波入射角不同时,散射系数随散射角的变化关系Fig.7 σ vs. θs with different θi

由图7可见:当θi为30°,45°,60°时,复合散射系数分别在它们各自的镜反射方向处,即θi在30°,45°,60°处达到最大值,且不难看出,复合散射系数在镜反射方向的峰值随入射角的增大而增大;复合散射系数在散射角θs>0时受电磁波入射角影响较大,40°>θs>0°时,有θi越大、σ越小的规律;而在50°>θs>40°时,θi=45°时的σ最大,θi=30°时的σ最小;θs>50°,又有θi越大、σ越大的规律。除去上述的几个范围之外,σ受θi的影响较小。

2.6粗糙面间距对散射系数的影响

分别取两粗糙面间的距离d=15λ,30λ,45λ,保持其他条件不发生变化,分析计算两粗糙面间距离d不同时,散射系数随散射角的变化关系,如图8所示。

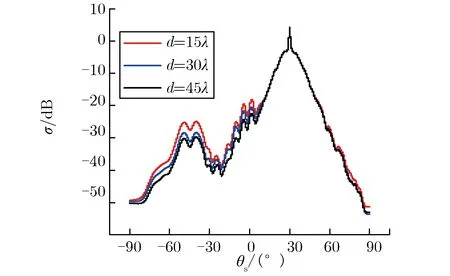
图8 两粗糙面间距离不同时,散射系数随散射角的变化关系Fig.8 σ vs. θs with different d

由图8可见:粗糙面间距离d对散射系数σ产生的影响较为显著,当15°<θs<60°时,散射系数σ几乎不随d的变化而变化;θs在其他变化范围内,σ随d的增大而减小。这是因为分层粗糙面自身的散射特性发生了变化,粗糙面间距变大,分层粗糙面的散射特性变弱,进而影响到了复合散射系数σ的大小。

3 结论

本文采用蒙特卡罗方法生成了遵守指数分布的分层土壤表面,使用矩量法研究了分层粗糙面与上方运动目标的复合散射问题,计算了分层土壤粗糙面与上方圆形截面柱目标在锥形波入射下的复合散射特性。结果表明,圆形截面柱在分层土壤表面上方纵向平移、斜向平移时对复合散射系数的影响比较显著,而横向平移对复合散射系数造成的影响较小。目标运动不仅会改变自身的散射特性,且会影响到目标与粗糙面之间的耦合,复合散射特性可为诸多工程技术问题[16-18]提供可用的实践方法和必要的理论依据。本文还有许多值得改进的地方,如本文只研究了分为两层的分层粗糙面模型,且目标只在粗糙面的上方进行移动,自然界中的目标绝不会仅在粗糙面上方进行移动,也不会只有规则的图形;以海面为例,目标极有可能会在海面下方进行运动,对于此类海(地)粗糙面与置于其上方或下方运动目标的复合散射问题,将是今后的研究方向之一。