全电磁粒子模拟算法研究及软件研制进展
2023-10-20陈再高
陈再高
(强脉冲辐射环境模拟与效应全国重点实验室;西北核技术研究所: 西安 710024)
全电磁粒子模拟方法通过求解带电粒子与电磁场之间的耦合方程,能准确描述电磁场随时间的演化过程及带电粒子的运动参数,在等离子体相关物理现象研究[1]、真空电子器件的设计与优化[2-3]、介质击穿模拟[4]及核爆炸人工辐射带模拟[5]等方面得到了广泛应用。此外,高能射线作用于飞行器等电子设备,在电子系统内外激发光电子或康普顿电子,由于电荷分布不均匀,飞行器表面会产生较大的置换电流,最终在系统周围,甚至内部激励强电磁脉冲,全电磁粒子模拟方法也能用于模拟高能射线产生系统电磁脉冲等物理现象[6-7]。国内外均开展了全电磁粒子模拟算法的研究及软件的研制,其中,国外研究机构和企业研制了MAGIC[8]、KARAT[9]和CST[10]等全电磁粒子模拟软件,国内西北核技术研究所和西安交通大学联合研制了2.5维粒子模拟软件UNIPIC[11]和3维并行粒子模拟软件UNIPIC-3D[12],电子科技大学研制了3维粒子模拟软件CHIPIC[13],中国工程物理研究院研制了粒子模拟软件NEPTUNE[14],这些软件在高功率微波源器件的设计及参数优化方面发挥了重要作用。
在全电磁粒子模拟软件中,电磁场方程一般采用时域有限差分 (finite difference time domain,FDTD)方 法,该方法的计算量与网格数呈线性关系,具有程序实现相对简单及容易并行等优点。FDTD方法采用正交结构网格。传统的阶梯网格处理复杂边界会带来偏差,而共形网格能精确描述复杂器件结构的边界,基于共形网格的FDTD方法能大幅提高复杂结构的计算精度[15]。因此,在全电磁粒子模拟算法中引入计算机辅助设计技术,实现共形网格的自动化生成,能大幅提高全电磁粒子模拟算法计算复杂结构的精度。此外,将全局优化算法与全电磁粒子模拟算法结合,能实现真空电子器件几何参数及电学参数的全局优化[16-17]。
最新发展的时域间断有限元方法在Maxwell方程的弱解积分形式中引入数值通量,通过方程离散获得非结构网格单元内电磁场的推进公式,每个单元中的电磁场值只与相邻单元有关,不用求解全域矩阵的逆。时域间断有限元算法能采用非结构网格描述复杂结构边界,同时具备FDTD方法显式求解方程的优点,将间断有限元引入到全电磁粒子模拟算法,能大幅提高复杂几何模型的处理能力,同时,在电磁场的时域求解方程中引入了电势矫正方程,能减少时域间断有限元全电磁粒子模拟方法中电荷不守恒带来的偏差,这是粒子模拟方法研究的热点。
本文介绍了作者所在团队在全电磁粒子模拟方法研究及软件研制方面取得的进展,通过20多年的技术研究及软件研制,研究了基于计算机辅助设计的共形结构网格生成技术,研制了2.5维全电磁粒子模拟软件UNIPIC及3维全电磁粒子模拟软件UNIPIC-3D,基于并行遗传算法及2.5维粒子模拟算法研制了真空电子器件优化设计软件,开发了基于时域间断有限元的2.5维全电磁粒子模拟程序。
1 2.5维全电磁粒子模拟技术
2.5维粒子模拟软件UNIPIC软件主要用于模拟真空电子器件内部的电磁波与相对论电子束之间的非线性相互作用,包括非相对论与相对论范畴的束-波互作用物理现象[11]。UNIPIC软件可模拟的2维问题包括x-y,z-r,r-φ3种坐标系;能设置理想导体、有耗导体、注入波及吸收波边界等边界条件,可通过热发射、场致发射、二次电子发射、爆炸发射及光电发射等方式产生带电粒子。另外,UNIPIC软件还能模拟带电粒子与中性气体的弹性、电离、激发、电荷交换及复合等碰撞现象[18-19]。本文作者所在团队将UNIPIC软件的核心计算模块与并行遗传算法相结合,研制了真空电子器件并行优化软件。
1.1 UNIPIC软件的数值算法
图1为全电磁粒子模拟核心算法流程框图。UNIPIC软件中电磁场由Maxwell方程描述,带电粒子运动由Newton-Lorentz方程描述,Maxwell方程与Newton-Lorentz方程之间的耦合采用CIC(cloud-in-cell)插值算法。采用FDTD方法求解电磁场随时间的演化过程,每隔一定时间步用Maxwell方程的散度方程进行偏差校正。FDTD方法的时间步长受稳定性条件的限制,在算法上选用中心差分的显式格式,通过加入阻尼因子实现时偏格式,进一步减少电磁场计算带来的数值噪声。初始电磁场可采用输入参数或输入文件的方式加载,也可通过求解Poisson方程获得。UNIPIC软件具有直角坐标系、柱坐标系及极坐标系下2维Poisson方程求解功能。
在2维模拟中,粒子由2维坐标和3维速度表示,采用Boris提出的“半加速-旋转-半加速”方法求解。依据电磁场的稳定性条件,粒子的推进距离不超过一个网格,网格边界处粒子在一个时间步长内可能会出现穿过多个网格的情况,这时需要根据粒子运动轨迹与网格线的交点,分段计算粒子运动产生的电流。当带电粒子运动较慢时,采用多次电磁场推进/一次粒子推进的方式提高算法的计算效率。UNIPIC软件还具有加载任意分布初始粒子的功能。
由于电磁场及电流分布在离散的网格点或线上,而粒子位置则位于计算区域内任意位置,粒子推进时产生的电流需要分配到网格点或线上,推进粒子运动时粒子所在位置处的电磁场值需要通过网格点上的电磁场插值获得。为避免出现粒子的自推进现象,同时控制插值所需计算量,UNIPIC软件实现了一阶最近网格点插值及二阶双线性插值2种方式。由于插值会造成一定的数值偏差或噪声,软件对数值噪声进行滤波处理,减少长时间计算所带来的累积偏差。
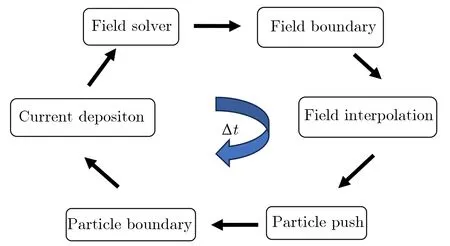
图1 全电磁粒子模拟核心算法流程框图Fig.1 Flow chart of fully electromagnetic particle simulation method
1.2 粒子模拟中碰撞电离数值模拟技术
在气体放电器件和填充等离子体器件中,气体分子、原子和带电粒子之间会发生碰撞,一般采用蒙特卡罗碰撞(Monte Carlo collision,MCC)模型来处理[18]。MCC是采用碰撞时间随机的方法,而PIC方法中粒子推进和场推进的时间步长是固定的,因此采用在一个时间步长内随机决定粒子间是否发生碰撞的方法来实现蒙特卡罗碰撞。
碰撞模型中的粒子分为靶粒子和源粒子。假设第i个源粒子和靶粒子之间可发生N种碰撞,设第j种(j∈[1,N])碰撞的碰撞截面为σj(εi),总碰撞截面为所有类型的碰撞截面之和,表示为
(1)
第i个源粒子与靶粒子发生碰撞(包括所有N种碰撞)的概率,即碰撞总概率可表示为
Pi=1-exp[-σT(εi)nt(xi)viΔt]
(2)
其中:xi,vi分别为第i个源粒子的位置和速度;nt(xi)为第i个源粒子位置处靶粒子的数密度;Δt为PIC推进的时间步长。
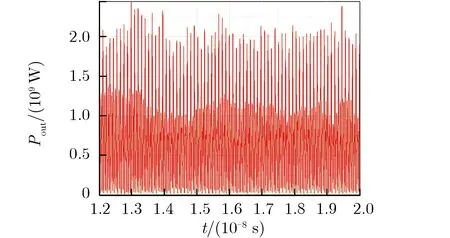
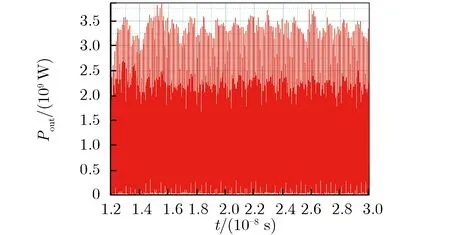
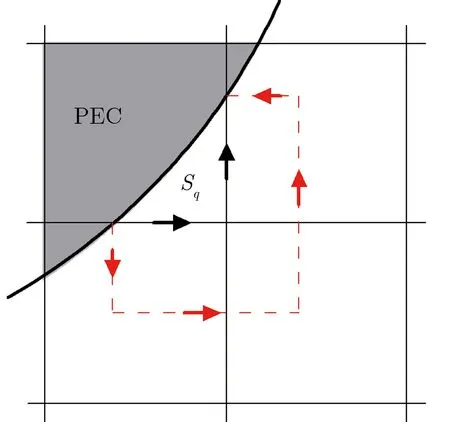
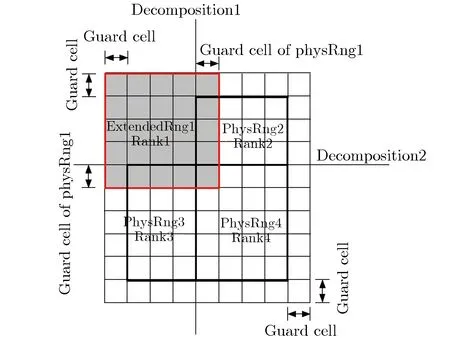
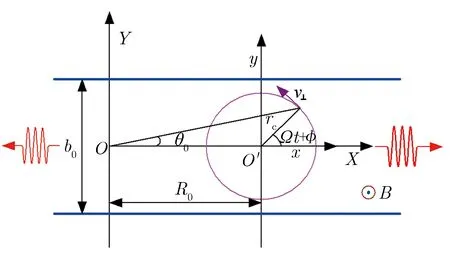
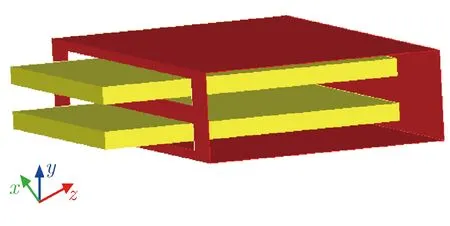
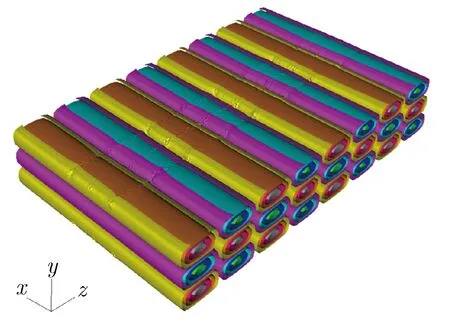
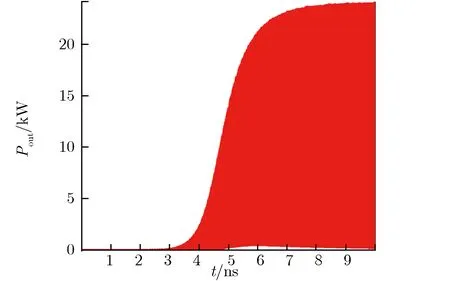
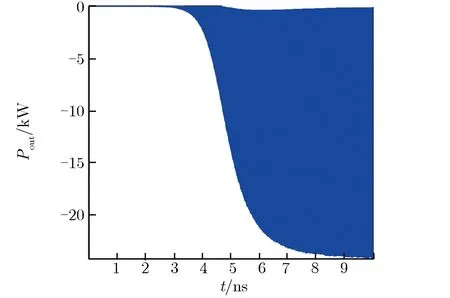
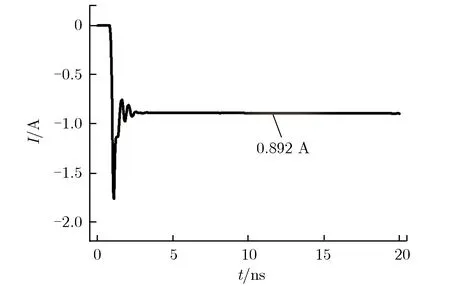
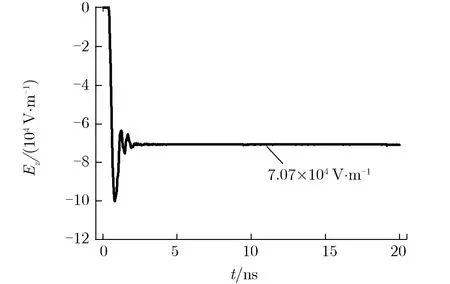
为避免在每次推进中对每个源粒子进行大量计算,在PIC-MCC方法中引入空碰撞概念。碰撞总概率可设定为一个常数Pnull,每次推进时只需随机抽取部分源粒子进行碰撞处理。随机抽取时,对每一个源粒子产生一个随机数R1(R1∈[0,1]),如R1 表1 粒子碰撞类型的选择Tab.1 Selection of particle collision types 其中:υj为源粒子与靶粒子可能发生的第j种碰撞类型的概率;υ′为总碰撞概率。程序能处理多种碰撞过程,包括电子与中性原子的弹性碰撞、电子与中性原子的激发碰撞、电子与中性原子的电离碰撞、离子与中性原子的弹性碰撞及离子与中性原子的电荷交换碰撞等过程。在各种碰撞类型中,需处理碰撞后各粒子的位置、速度和方向。以电子与中性原子的弹性碰撞为例,碰撞后电子的运动方向是随机的,散射角χ和子午面角φ为可表示为 (3) 其中:R3,R4为随机数(R3,R4∈[0,1]);E为入射电子能量。 碰撞后电子的速度可表示为 (4) 其中:me,mi分别为电子和离子的质量;v为入射电子速度。 遗传算法是一种全局优化算法,将全电磁粒子模拟算法与遗传算法相结合,能实现真空电子器件的全局优化设计。在采用遗传算法对相对论返波管(relativistic backward wave oscillator,RBWO)进行优化时,需将全电磁粒子模拟程序模块计算得到的RBWO输出功率作为每一个个体的适应度。由于计算适应度值要模拟改变结构参数后的RBWO模型,直到器件有稳定的功率输出,并通过输出功率的平均值得到该个体的适应度值,导致每个个体适应度值的计算时间较长。研制的真空电子器件优化软件采用并行遗传优化算法[16-17, 20],该方法能在国产超算上同时计算每个个体的适应度值,节省优化设计所需的时间。 图2为RBWO并行优化遗传算法流程框图。 图2 RBWO并行优化遗传算法流程框图Fig.2 Flow chart of parallel genetic algorithm for RBWO 在遗传算法中需要生成大量的伪随机数,软件采用单独的一个进程(主进程)负责伪随机数的生成,采用其他进程(子进程)完成适应度值的计算。在第一步时,主进程读取优化参数设置的取值范围,并通过伪随机数生成算法为每个优化的参数在取值范围内产生一组新的参数值,同时对参数进行浮点数编码;主进程将新生成的参数分组,每一组均包含了所有需要优化的参数,将每一组参数发送给相应的子进程;所有子进程均执行第二步,每一个子进程通过接收的参数生成新的RBWO模型文件,调用全电磁粒子模拟计算模块读入模型文件进行数值计算,并将器件的输出功率求平均值,得到该个体的适应度值,最后将计算的适应度值发送给主进程;主进程单独执行第三、四、五步,主进程在获取每个个体的适应度值后,首先将适应度值最大的个体挑选出,并对剩下的个体进行选择操作,如果某一个体的适应度值较大,则它被选择存活到下一代的概率就变大,如图2的第三步所示;主进程以一定概率将参数进行交叉以及变异操作产生新的参数,如图2的第四步、五步所示;最后主进程将新生成的优化参数值再次分组,并将生成的参数值再次发送给子进程;每个子进程均需要执行第六步,每个子进程根据接收到的参数值,生成新的RBWO模型文件,子进程调用全电磁粒子模拟计算模块读入模型文件进行模拟计算,获得该个体的适应度值,并再次发送给主进程。在第七步,主进程在接收到每个子进程发送的适应度值后,判断最佳优化结果是否满足指标要求,如果不满足最优指标则跳往第三步开始下一轮的参数优化,直到完成目标优化并输出优化结果。 RBWO是一种能量转换效率非常高的真空电子器件,在设计过程中需调节的参数非常多[20],可采用本文建立的优化方法对RBWO的慢波结构进行自动优化。慢波结构底部沿着r方向高度的取值范围为0.011~0.015 m,顶部的取值范围为0.015~0.02 m。对RBWO慢波结构的9个底部位置和9个顶部位置所对应的高度进行浮点数编码,模型的其他参数和驱动电压保持不变,初始种群数设置为80,进化50代后,就可得到RBWO慢波的优化结构。采用UNIPIC软件模拟优化前均匀慢波结构及优化后非均匀慢波结构返波管模型,优化前后,返波管的平均输出功率如图3所示。均匀慢波结构RBWO的模拟结果如图3(a)所示,结果表明在12 ns后输出的平均功率为760兆瓦;优化慢波结构参数后,在12 ns后输出的平均功率为1.16 GW,如图3(b)所示,输出功率相比优化前能够提高52%。数值模拟结果表明,2.5维粒子模拟软件UNIIPIC能够准确模拟轴对称真空电子器件,同时融合了并行遗传算法的全电磁粒子模拟算法,能用于真空电子器件的优化设计。 (a) Original (b) Opitimized图3 优化前后,RBWO的平均输出功率Fig.3 Average output power of original and optimized RBWO 3维并行粒子模拟软件UNIPIC-3D软件可用于模拟3维真空电子器件内电磁波与相对论电子束之间的非线性相互作用[8-9]。软件集成的计算机辅助设计工具能用于构建复杂的3维几何模型,实现的结构网格剖分模块沿着x,y,z方向对复杂3维模型进行共形结构网格剖分,采用区域分解算法实现了核心计算模块的并行计算。软件能设置理想导体、有耗导体、端口模式加载及完全匹配层等电磁场边界条件,带电粒子可通过场致发射、束发射及爆炸发射等方式产生带电粒子。 随着真空电子器件工作频率的提高,特别是器件的工作频率达到太赫兹波段,真空电子器件的高频结构也会变得更精细,通过缩小网格的尺寸能提高计算的精度,但会导致器件模拟计算量的大幅增加。因此,为更准确地描述真空电子器件中的细小结构,提高软件模拟复杂器件结构的计算精度,采用共形磁场计算技术提高复杂结构器件的模拟计算能力。研制的3维粒子模拟软件采用了基于ECT-CFDTD(enlarged cell technique conformal FDTD)原理的电磁场共形计算方法,通过基于计算机辅助设计方法的射线追踪方法,获得网格线与几何体的交点,这些交点、网格顶点及几何体之间的拓扑关系共同构成了共形网格系统。在共形网格系统中定义了几何量及物理量之间的拓扑关系,采用ECT-CFDTD方法将所有离散的电磁场方程转换为局部有限积分方程,避免了求解大型矩阵,并保持不同区域的推进方程具有相同的表达方式。 ECT-CFDTD方法的基本原理如图4所示。 (a) Conformal grid used in CFDTD method (b) Conformal electron emitter图4 ECT-CFDTD方法的基本原理Fig.4 Basic principles of the ECT-CFDTD 当对面积为Sp的小面元计算电磁场时,电场的推进方程保持与经典的FDTD方法相同,只对磁场的推进方程进行修改,该方法能在有效保证器件模拟计算精度的同时,无须大幅减少时间步长。当网格中真空所占面积较小时磁场的计算方法可表示为 (5) (6) (7) (8) (9) (10) 采用3维全电磁PIC粒子模拟软件模拟真空电子器件需耗费的计算资源非常多,采用并行计算的方法能同时使用多个进程对同一个器件模型进行模拟,大幅减少器件模拟所需的时间。研制的3维并行粒子模拟软件采用规则分区的方式实现了粒子模拟软件中电磁场计算的并行化。首先,在不同的方向上定义不同的分割位置;然后,根据分割位置,将全局网格区域分割为多个子区域,每个子区域对应一个物理区域,同时也对应唯一的进程标号;同时,在物理区域定义的基础上,定义了与物理区域对应的扩展区域,用于给出当前进程的局部网格区域。 以2维情况下的区域分解算法为例,图5为并行计算的区域分解及扩展网格层。 (a) Computational domain decompostion (b) Extented grid layer of physical domain图5 并行计算的区域分解及扩展网格层Fig.5 Domain decomposition and extended grid layer by parallel computation 由图5(a)可见,由Decomposition1和Decomposition2定义了2个分割位置,将全局网格分割为4个区域,同时也将全局物理区域分割为4个子物理区域,分别标示为PhysRgn1,PhysRgn2,PhysRgn3,PhysRgn4,分别对应进程1、进程2、进程3和进程4。将物理区域的上下边界各扩展一层为物理区域添加守护网格层,图5(b)所示为进程1所计算的PhysRgn1区域扩展得到的局部网格区域ExtendedRgn1。每一个进程的扩展网格区域与其他进程的物理区域进行求交运算,若当前进程的扩展网格区域与某个进程的物理区域求交运算结果不为零,则需进行电磁场数据的交换。 在上述规则分区的基础上,实现了带电粒子的并行推进。在每一个时间步长内,每个进程推进所计算物理区域内部所有带电粒子的运动方程,确定带电粒子经单个时间步后的速度和位置;由带电粒子推进后所处的位置,判断是否将该带电粒子发送至其他相邻进程,当带电粒子位于当前进程的守护网格区域时,就需将粒子信息发送给相邻网格区域的进程。 采用自行研制的3维共形全电磁粒子模拟软件对双电子注平板回旋管进行了数值模拟研究,图6为双电子束平板回旋管示意图[21]。平板回旋管的工作原理如图6(a)所示。图6(b)中,黄色标示为带状回旋电子束,红色为平板回旋管的金属结构。两个带状电子回旋电子束回旋中心在y方向的位置分别位于y=b0/6和y=5b0/6,每一个带状回旋电子束的线电流密度均为18 A·cm-1。网格数为240×60×380,在国产超级计算机上采用228个进程进行并行计算,得到电场强度Ex的3维空间分布、平板回旋管输出功率随时间的变化关系及电子的实空间和相空间分布,分别如图7-图9所示。 (a) Projection of electron orbit in the planar gyrotron (b) Planar gyrotron with double-beam图6 双电子束平板回旋管示意图Fig.6 Schematic diagram of double-beam planar gyrotron 图7 电场强度Ex的3维空间分布Fig.7 3D distribution of Ex (a) Output power in x direction (b) Output power in -x direction图8 平板回旋管输出功率随时间的变化关系Fig.8 Output powers of the planar gyrotron vs. time (a) In real space (b) In phase space 由图7可见,Ex在z方向的相位变化呈8π正弦稳态分布,y方向的相位变化为3π正弦稳态分布,电磁场的分布模式稳定,没有出现模式竞争问题。 由图8可见,2个端口处输出的功率大小相同,因功率输出的方向相反,依据功率的计算公式所得到的幅值相反,输出的总功率为24.2 kW。由图9可见,随着带状回旋电子束沿着z轴方向传输,经与电磁波的相互作用,电子束在角向发生速度调制,将电子束的动能转化为电磁波能量。 研制了基于时域间断有限元空间的2.5维全电磁粒子模拟程序,通过引入辅助矫正势抑制了电荷不守恒所带来的偏差[22-23]。程序采用三角形网格对计算区域进行非结构网格剖分,实现了基于标量基函数及矢量基函数的电磁场时域间断有限元算法,采用总场/散射场边界条件实现了电压波加载边界,采用复频率完全匹配层实现了端口的截断边界条件,同时实现了轴对称和金属壁等电磁场边界条件。针对非结构网格中带电粒子与电磁场之间的相互作用,实现了带电粒子的快速定位及电荷和电流分配算法。 (11) (13) 再次应用分部积分,得到 (14) (15) 其中,算子〈·〉,[·]的定义为 上标“+”表示在邻接单元表面上电磁场值。 为了减少电荷分配不守恒带来的偏差,在程序中采用了最近发展的修正势Maxwell方程[24],表示为 (16) 其中:Φ,Ψ为修正势,它们及相关辅助方程的引入是为减小数值计算中电荷不守恒带来的偏差;κ和γ为修正系数。由式(16)可知,当Φ→0,Ψ→0时,方程退化为Maxwell方程。 从式(16)可推导得到 (17) 式(17)表明修正势Φ和Ψ可用来描述电荷不守恒和磁荷不守恒的偏差,且这种偏差以波的形式传递。当参数κ>1,γ>1时,由式(17)可知,偏差的传播速度远高于电磁波的速度。因此,在求解带有修正势的Maxwell方程时,电荷不守恒及磁荷不守恒引起的偏差会以非常快的速度传播到计算区域之外。含修正势的Maxwell方程间断伽辽金形式的离散与不含修正势Maxwell方程间断伽辽金形式的离散具有相同的步骤,各场量的空间近似仍采用Lagrange插值,在单元边界上数值通量的计算会因引入修正势而有所变化。 全电磁粒子模拟算法在计算带电粒子受到的洛伦兹力时,将带电粒子看成半径无限小质点,需计算粒子所在位置处的电磁场值,并代入到洛伦兹力公式中,得到电磁场对带电粒子的作用力。该电磁场值通过粒子所在单元及邻近单元上的电磁场的空间插值得到。为得到粒子所在位置处的电磁场,需知道粒子所在物理单元的编号及粒子在该单元内的局部坐标。为根据粒子的物理坐标快速查找粒子所在的单元编号,程序对计算域内的所有非结构网格单元采用了空间分群策略。将整个计算区域均匀划分为由Nx×Ny个直角网格构成的虚拟结构网格,并将与同一个虚拟网格有空间重叠的非结构三角单元组合为一个群。由于虚拟网格排列较为规则,通过粒子的物理坐标,可快速计算粒子所在虚拟结构网格的索引,进而获得粒子所在单元三角形网格群,提高在非结构网格中定位粒子的效率。确定粒子所在的三角网格单元后,根据等参单元与物理单元的坐标变换公式计算得到粒子在等参单元上的局部坐标,表示为 (19) (20) 获得粒子所在等参单元的局部坐标后,其所在位置的电磁场可表示为 (21) 带电粒子运动产生的电流作为电磁场方程的源项,假设宏粒子为具有一定大小的球形粒子,每个宏粒子的空间分布函数表示为 (22) 其中:α为空间分布多项式函数的指数项,R为设置的带电粒子影响半径,r为需计算电流分布所在位置的坐标 ;r0为粒子中心位置坐标。S(r-r0)在|r-r0|∈[0,R]范围内的积分为1,宏粒子运动产生的电流密度可表示为 I(r-r0)=evS(r-r0) (23) 其中,e为宏粒子所带电荷量。宏粒子电荷密度的空间分布可表示为 ρ(r-r0)=eS(r-r0) (24) 采用自行研制的2.5维时域间断有限元全电磁粒子模拟软件对同轴真空二极管进行了数值模拟,图10为真空二极管计算模型的剖面图。其中,二极管端注入电压为1 kV,上升沿为0.5 ns,沿着轴向的引导磁场强度为1.0 T,二极管同轴注入端的内外半径分别为5 cm和5.9 cm,同轴二极管阴极环面的内外半径分别为2.4 cm和2.7 cm,阴阳极板之间的距离为0.5 cm。对二极管进行了2维非结构网格的剖分,网格平均尺寸为1 mm。 (b) Triangular grid of vacuum diode图10 真空二极管计算模型Fig.10 Simulation model of vacuum diode 对二极管阴极面的发射电流及阴极发射面r=2.65 cm位置处的法向电场强度进行了诊断,模拟结果如图11所示。由图11(a)可见,稳定后的电流为0.892 A;由图11(b)可见,稳定后的电场强度为70.7 kV·m-1。 采用UNIPIC软件对相同的物理模型进行了数值模拟得到,稳定后的阴极电流为0.901 A,与间断有限元全电磁粒子算法模拟结果的相对偏差为1%;计算得到稳定后的电场强度为73.3 kV·m-1,与时域间断有限元全电磁粒子算法模拟结果的相对偏差为3.6%。主要原因是两套代码在处理电流发射时均采用了唯象的Gauss电子爆炸发射模型,该模型需计算阴极面附近位置处的法向电场强度及阴极发射面位置处的电荷密度。在UNIPIC软件中,法向电场值为距阴极面半网格长度位置处的电场值,同时电荷分配在正交网格的顶点处;在2.5维间断有限元全电磁粒子模拟算法中,采用的是非结构三角形网格。2种算法的计算结果仍能保持一致,表明时域间断有限元全电磁粒子模拟算法能用于真空电子器件的数值研究。 (a) Beam current vs. time (b) Electric field strength along z direction vs. time图11 2.5维时域间断有限元粒子模拟程序计算结果Fig.11 Simulation results by 2.5D particle-in-cell code basedon discontinuous Galerkin time-domain method 20多年来,本文作者所在团队在全电磁粒子模拟算法研究及软件研制方面取得了系列进展:(1)研制了基于计算机辅助设计的2.5维全电磁粒子模拟软件,开发了融合并行遗传算法和全电磁粒子模拟算法真空电子器件的优化软件,具备对RBWO等真空电子器件的结构参数及电学参数的优化能力;(2)研制了3维并行共形粒子模拟软件,具备复杂模型建模及数值模拟能力,能在国产超级计算机上对真空电子器件开展全尺寸3维结构的数值模拟研究;(3)发展了时域间断有限元全电磁粒子模拟技术,采用非结构三角网格实现了器件结构的精确描述,大幅提高了全电磁粒子模拟模拟软件计算真空电子器件的计算精度。 下一步,将会持续开展磁流体力学、高能射线碰撞电离、多物理场耦合及人工智能赋能等离子体数值模拟等先进数值模拟技术研究,进一步拓展粒子模拟软件在系统电磁脉冲模拟、跨尺度等离子体模拟及高密度等离子体模拟等领域的应用研究。
1.3 基于并行遗传算法的全电磁粒子模拟算法

1.4 2.5维全电磁粒子模拟软件优化RBWO
2 3维全电磁粒子数值模拟技术
2.1 3维全电磁粒子模拟共形算法
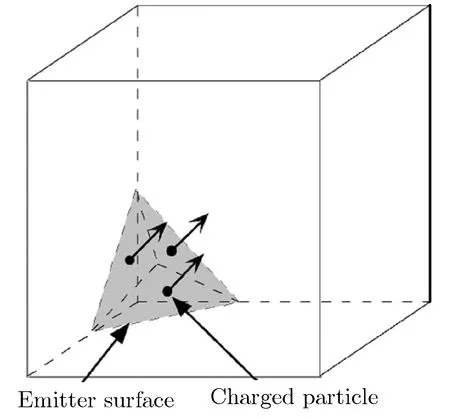
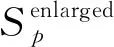
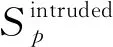
2.2 3维全电磁粒子模拟并行技术
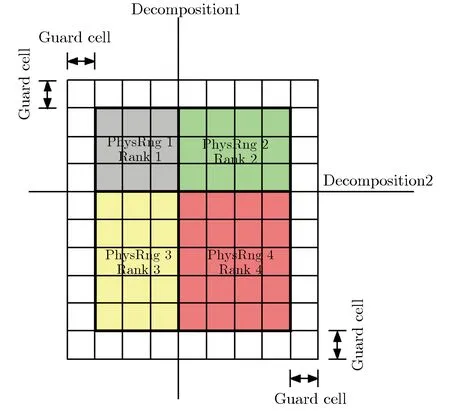
2.3 3维全电磁粒子软件模拟真空电子器件


3 基于时域间断有限元的全电磁粒子模拟技术
3.1 2维电磁场时域间断有限元算法
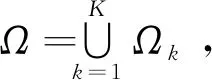
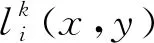

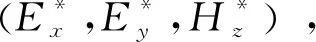
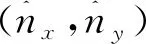
3.2 非结构网格中粒子快速定位以及电流计算
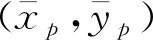
3.3 真空二极管间断有限元全电磁数值模拟研究

4 结论
