蒙特卡罗方法在核爆辐射环境模拟中的应用与发展

朱金辉,左应红,刘 利,牛胜利,商 鹏,李夏至,王学栋

(西北核技术研究所,西安 710024)

核辐射是核爆炸特有的杀伤因素。核爆炸的裂变核反应和聚变核反应过程会产生多种具有强辐射性质的辐射源,包括瞬发核辐射粒子、缓发核辐射粒子及裂变产物衰变释放的射线粒子[1-2]。核爆炸辐射源在爆心周围大气或介质中传输,与大气或介质相互作用形成核辐射场,可采用具有一定时空分布的辐射环境参数进行描述,如辐射剂量、粒子注量、能谱、时间谱及角度谱等[3-6]。不同爆炸场景的核辐射环境特征差异较大,大气层核爆炸与高空核爆炸是2类典型爆炸场景[7-9]。大气层核爆炸场景中,按时间维度可将辐射环境分为持续时间较短的瞬发核辐射[10-11]、缓发核辐射及持续时间较长的放射性沾染[13-14]。高空核爆炸核辐射环境,可分为瞬时辐射环境与长期辐射环境,瞬时辐射环境包括中子、γ射线、X射线及核电磁脉冲[15]等,长期辐射环境包括碎片云、附加电离层和人工辐射带等[16-17]。

核爆炸辐射环境场的特征取决于核辐射粒子在介质中的输运过程,即辐射粒子与物质发生相互作用的过程。研究核爆炸辐射环境最常用的方法是模拟粒子输运的蒙特卡罗方法[18-20]。蒙特卡罗方法,又称随机模拟方法,是通过直接跟踪模拟大量粒子的运动轨迹,利用随机数模拟粒子输运中的随机过程,抽取碰撞时的靶核、碰撞类型及出射角等参数,统计粒子运动过程中对待求物理量的贡献,获得统计性结果。采用蒙特卡罗方法可实现核爆炸辐射环境的输运计算。

本文作者团队长期从事核爆炸辐射环境的理论与数值模拟研究,运用蒙特卡罗方法解决了核爆炸辐射环境模拟中遇到的难点技术问题,发展了一系列数值计算模型和方法,在大气层和高空核爆炸辐射环境方面都取得了相应进展。本文将详细介绍蒙特卡罗方法在大气层核爆炸复杂条件下的瞬发和缓发辐射环境高效高精度数值模拟方面,高空核爆炸X射线、附加电离层、人工辐射带和核电磁脉冲等辐射环境数值模拟方面的应用和发展情况。

1 蒙特卡罗方法在大气层核辐射环境模拟中的应用与发展

大气层核辐射环境模拟计算需解决不同辐射源在大范围近地面环境中的模拟问题,涉及复杂条件和深穿透等问题。在长期实践中,本文作者团队针对相关具体问题发展了一系列蒙特卡罗减方差方法和建模方法,在大气层核辐射模拟中得到了较好的应用。

1.1 用于大气层核辐射深穿透问题的权窗逼近方法

核爆炸产生的早期核辐射环境在地面附近大气中影响范围可达3～5 km,而核爆炸产生的中子、γ射线在近地面大气中的自由程为百米量级。大空间范围内的早期核辐射输运问题属于典型的射线深穿透问题[1],对于此类问题,采用蒙特卡罗直接模拟方法难以获得可信的辐射环境参数。为在有限的时间内获得预定的计算精度,建立了栅元权窗结合密度逼近迭代的减方差方法。首先建立γ射线长距离输运分层模型,并合理设置计算区域几何网格。图1为γ射线近地面长距离输运示意图。通过不同密度条件下的多次迭代计算,利用非深穿透输运计算得到的权窗逐步生成更优的适合深穿透输运计算的权窗。利用权窗重要性函数引导粒子的分裂与轮盘赌,并采用环探测器记录,实现了γ射线在低空稠密大气中(含地面反照)长距离输运的蒙特卡罗模拟。

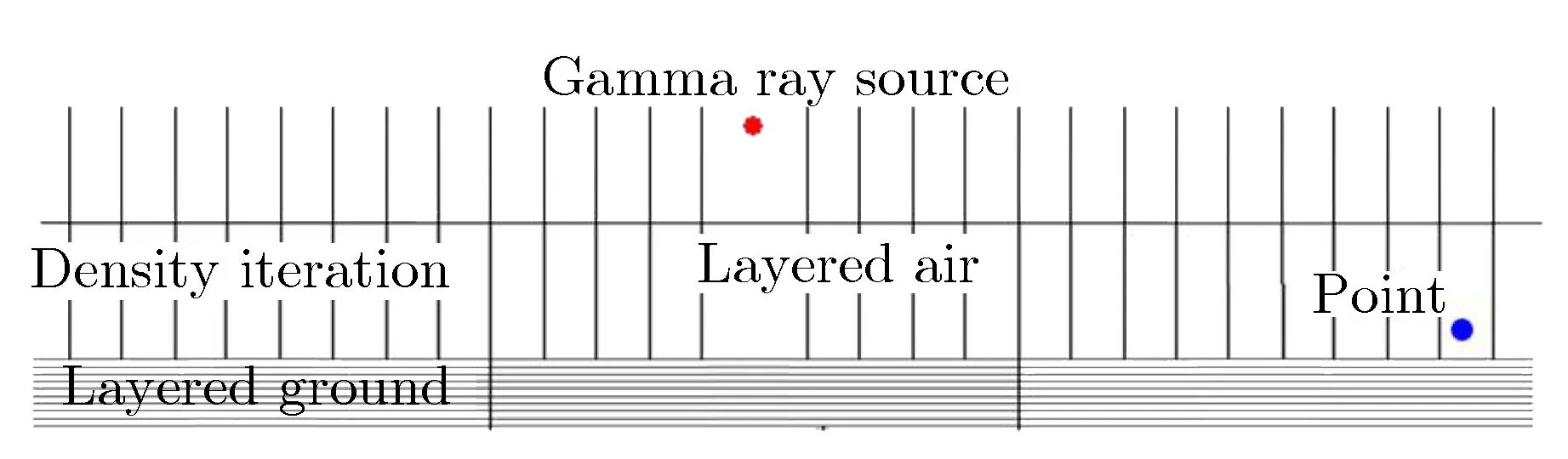
图1 γ射线近地面长距离输运示意图Fig.1 Diagram of long distance γ-ray transport near ground

采用上述栅元权窗结合密度逼近迭代减方差方法,计算了离地面400 m的γ射线在爆心投影点周围5 km范围内输运形成的地面γ射线辐射场,通过多次密度迭代,最终给出实际密度条件下的计算结果。栅元权窗减方差方法,γ注量Φγ及相对偏差σr随测点距离d的变化关系如图2所示。5 km测点的注量、相对偏差及FOM因子F随模拟粒子数Np的变化关系如图3所示。由图2和图3可见,该减方差方法模拟得到γ射线注量的相对偏差小于5%,反映计算效率的FOM因子随模拟粒子数的增长而保持稳定,表明该减方差方法可有效解决γ射线长距离输运的模拟问题。

上述方法的核心是通过迭代计算得到合适的权窗参数,对中子在大范围空间内输运的深穿透问题,该方法同样适用。对于介质密度变化不大的模型,可采用网格权窗替代栅元权窗以降低建模的复杂性,同时应用密度逼近迭代方法获取优化的网格权窗参数,进而对中子、γ射线输运进行引导。

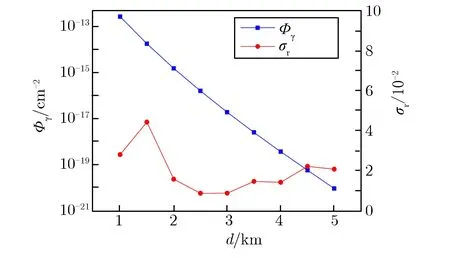
图2 栅元权窗减方差方法,γ注量及相对偏差随测点距的变化关系Fig.2 Φγ and σr vs. d by using cell-based weight window variance reduction method

(a) Φγ vs. Np

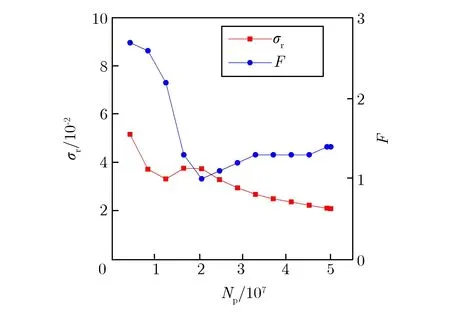
(b) σr and F vs. Np

1.2 传输介质变化条件下缓发γ辐射输运自适应建模方法

核爆炸早期核辐射中的缓发辐射源是随时间变化的复杂体源,最主要成分为裂变碎片衰变释放的γ辐射。缓发γ辐射在传输中会受冲击波扩展过程的影响,冲击波会使爆心周围一定范围内的空气密度分布发生变化,导致缓发γ辐射剂量出现流体力学增强效应[5]。

为计算流体力学增强效应对γ射线输运的影响,建立了冲击波导致传输介质变化条件下的缓发γ辐射大气输运自适应建模方法。在冲击波在特定时刻形成的大气密度场分布条件下,现有γ辐射大气输运几何模型通常划分为多个均匀步长网格,难以反映波阵面处大气密度的剧烈变化。同时在大气密度变化平缓区域划分了过多的网格,降低了模型描述的精确性和增加了几何栅元。针对上述问题,利用自适应方法将均匀步长网格调整为非均匀步长网格,即针对大气密度变化较大的区域增加了网格数目,避免了等步长网格中因步长设置过大而导致的几何模型精确性降低;针对大气密度变化不大的区域减少了网格数目,避免了等步长网格中过多的几何栅元而导致计算量的增加。

针对10 kt当量爆炸冲击波在爆后0.2 s时的大气密度分布函数,取步长为64 m和步长4 m分别构建均匀粗网格模型和细网格模型。同时以64 m为默认步长构建自适应网格模型,建立一个半径为2 km的1维球对称几何模型,大气为理想均匀大气,密度为1.225 kg·m-3。1维球对称几何模型的3种网格划分方法如图4所示。

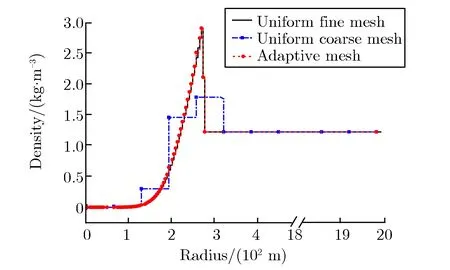
图4 1维球对称几何模型的3种网格划分方法Fig.4 Three grid partitioning methods for 1D spherically symmetric geometric models

采用蒙特卡罗模拟程序开展上述1维球对称几何模型的γ辐射输运计算,并沿径向在大气密度变化较大的150～350 m范围内均匀布放21个探测点。模拟粒子数设置为1.0×107。建立的γ辐射1维球对称几何模型栅元数和对应的模拟计算时间如表1所列。

表1 1维球对称几何模型栅元数和对应的模拟计算时间Tab.1 Number of grid elements and simulation time for one-dimensional spherically symmetric geometric model

以步长为4 m的均匀细网格模型为基准,计算得到自适应网格模型和均匀粗网格模型与基准值(均匀细网格模型)相对偏差随距离的变化关系,如图5所示。由图5可见,在计算结果均收敛的情况下,自适应网格模型模拟结果与基准结果基本重合,平均相对偏差为0.13%,而均匀粗网格模计算结果与基准结果则出现了约为5%的相对偏差,平均相对偏差为2.9%,但自适应网格模型模拟计算时间较步长为4 m的均匀精细网格基准模型减少了52.0%。

该方法能有效减少几何栅元个数,节约大量的内存空间和计算时间。该方法采用自适应网格模型,在保证计算精确性的前提下,能有效提升模型计算效率,是一种既能精确描述大气密度分布情况,又尽量具有较少几何栅元的精细高效建模方法。该方法还可通过在γ辐射输运圆柱体模型的r-z方向进行2维自适应建模,适用于冲击波影响下的非均匀大气-土壤模型。

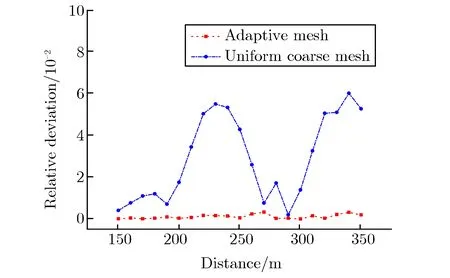
图5 自适应网格模型和均匀粗网格模型与基准值(均匀细网格模型)相对偏差随距离的变化关系Fig.5 Relative deviation of adaptive mesh model, and uniform coarse mesh model compared with the datum value (uniform fine mesh model) vs. distance

1.3 大规模复杂城市建模与基于网格的权窗减方差方法

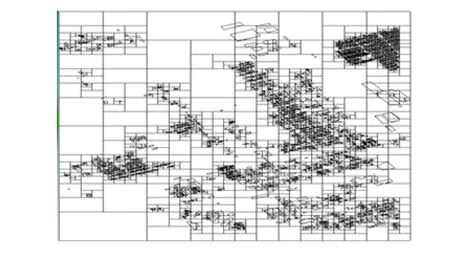
当核爆炸发生于城市场景,爆炸产生的中子、γ射线在城市中输运时,除受空气的散射外,还会受城市建筑物的散射、反射与衰减等复杂过程。准确计算城市大气层核爆炸产生的瞬发核辐射环境参数,主要面临2个难题:一是如何将大规模城市建筑物复杂几何批量转换为蒙特卡罗粒子输运计算模型;二是如何解决多栋建筑物厚屏蔽体及地表大气中数千米远距离输运的深穿透模拟问题。针对这2个难题,发展了基于GIS数据的自动化辐射输运城市几何建模技术及基于网格权窗的减方差模拟技术。

城市复杂条件下的辐射建模可分为4个步骤:(1)采用ArcGIS、freeCAD等进行后处理开发,将描述城市建筑物矢量轮廓的shapefile数据,自动转换为.step格式的3维几何模型;(2)在3维CAD模型中,将城市建筑的墙体及楼层板设置为一定厚度,如墙体厚为30 cm,楼层板厚为10 cm,目前的模型中忽略了窗户、门框及房间内部隔墙等细节;(3)采用SuperMC软件将.step模型转换为可供蒙特卡罗计算的输入卡,该过程中需进行几何交叠修复等模型预处理,并对地面混凝土几何进行建模,设置建筑材料、重要性及源等必要的计算参数;(4)手动完善蒙特卡罗计算的输入卡,如设置空气区域及空气密度,减方差设置等。

由于城市几何模型的尺度大、建筑物多、记录范围广,会出现深穿透现象,直接蒙特卡罗模拟时,离源较远区域位置的模拟结果相对偏差很大,因此基于网格的权窗,发展了针对城市核辐射粒子输运的减方差技术。该减方差技术主要有4个步骤:(1)设置一个用于产生权窗的环形栅元能量沉积计数:距离地面为1 m,高为5 m的靠近城市边界的包围整个2 km × 2 km模拟区的圆环;(2)模拟区域用mesh划分为同轴圆柱壳虚拟网格,柱面间距为40 m,圆柱中心轴垂直穿过爆心;(3)再进行直接蒙特卡罗模拟,依据各虚拟网格中粒子对环形栅元能量沉积计数结果的贡献计算得到权窗,必要时对权窗进行迭代优化;(4)通过权窗函数引导射线粒子输运至离爆心较远的区域,实现减方差模拟计算。图6为建立的城市条件下辐射输运几何模型。

针对某城市模型,当量为1 kt威力条件下,采用基于网格权窗减方差技术,模拟得到图7为典型城市大气层核爆炸瞬发γ剂量场计算结果,如图7所示。模拟粒子数为109,在未采用减方差技术时,相对偏差很大,采用减方差技术后,剂量计算结果的相对偏差明显降低,满足应用要求精度。

(a) Model geometry transformed by SuperMC

(b) Model used in MCNP input

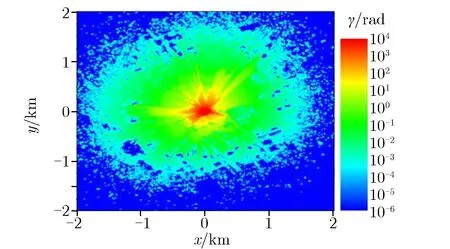
(a) No variance reduction

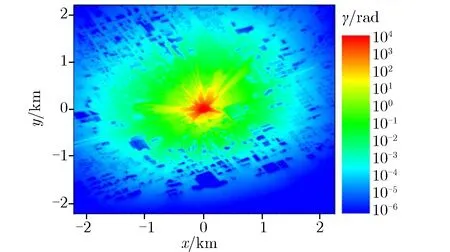
(b) Weight window based variance reduction

1.4 基于伴随输运的核辐射环境场模拟方法

在大气层核辐射环境模拟中,常需计算不同高度辐射源在地面附近产生的辐射场参数。采用常规正向输运模拟方法,需进行多次反复模拟计算。通过引入伴随输运模拟方法[21],可将求解一系列“单源-多探测器”的正向输运问题转换为求解一个“单探测器-多源”伴随输运问题,从而实现一次计算给出不同辐射源项条件下地面附近不同测点的辐射场参数。核辐射正向与伴随输运模型如图8所示。

(a) Forward transportation model

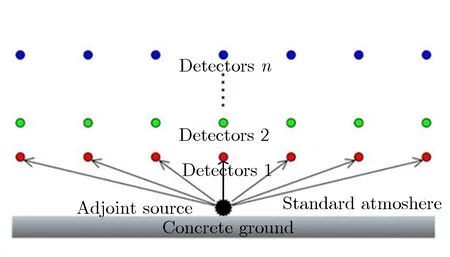
(b) Adjoint transportation model

伴随输运是正向输运的逆过程。在伴随输运方式下,从探测位置处抽取的伴随中子或γ首先被“赋予”某一权重,经与大气和地面相互作用的逆向输运模拟后,得到不同爆高和不同相对距离处的中子或γ的伴随注量。伴随输运给出的伴随注量具有反映正向源位置处中子或γ重要性参数的物理意义,即一个源中子或γ对探测器响应的贡献[22]。

实际计算中,地面伴随源项对不同高度H,不同距离S处的伴随注量对应于高度为H的源在距地面S处产生的辐射注量。

在伴随模型中,所有屏蔽介质的几何及材料属性均不发生变化,与正向模型保持一致,需改变的是源与探测器的相对位置及特性,在伴随模型中,伴随源位于正向模型中探测器的位置,即地面附近各向同性点源,伴随源的能量按照响应函数进行抽样;而探测器则位于正向模型中源的位置,针对具体问题可根据模拟需要设置一系列探测器。图9为一次伴随输运与多次正向输运计算结果的对比。由图9可见,二者吻合良好。从两种输运模式的计算时效性来看,无论是正向输运还是伴随输运,对于千米量级的长距离输运蒙特卡罗计算,都需使用减方差方法来加速问题收敛,且所需的计算时长也相当。需要说明的是,伴随计算目前只能采用多群方式进行模拟,计算精度与多群截面数据的精度相关。在上述算例中,伴随计算与正向输运的相对偏差大多小于15%,满足工程应用需求。由图9对比结果可见,利用蒙特卡罗伴随方法计算瞬发辐射环境参数,工程应用价值十分显著。

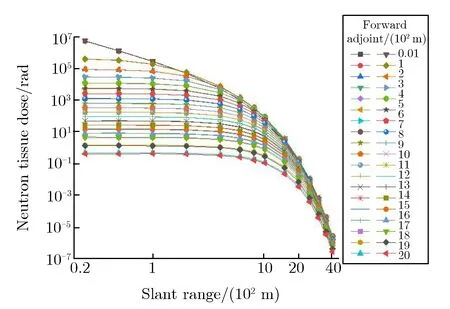
(a) Different height with the same source

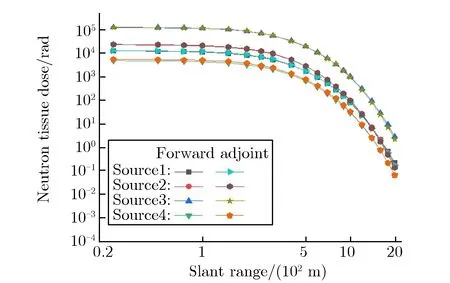
(b) Different source with the same height

1.5 大空间辐射场计算的全局减方差方法

在早期核辐射和近地面电磁脉冲源项计算中,往往需计算全空间辐射场。第1.1节中采用的局域减方差方法(local variance reduction, LVR)通常只针对特定目标探测器,难以给出理想的全空间辐射场。与之相比,全局减方差方法(global variance reduction, GVR) 通过全局权窗来控制全空间模拟粒子的分布,整体提高全空间计算效率,更适合全空间辐射场的求解计算。

在大气层核辐射环境模拟直接采用现有的全局减方差方法面临两个问题:一是现有全局减方差方法适用于等体积的栅元/网格,当计数栅元/网格体积差异较大时,体积大的栅元/网格内模拟粒子数较多,体积小的栅元/网格内模拟粒子数较少,使全局计算效率降低;二是计算边界附近的非计数区占用的计算资源较多,辐射场计算模型一般可划分为计数区和非计数区,非计数区域内模拟粒子可输运至计数区并影响其计数,将全局权窗参数统一应用于计数区与非计数区,非计数区内(尤其是土壤等吸收截面较大的介质内)模拟粒子过度分裂,占用较多计算资源。因此,本文提出基于体积和非计数区修正的全局减方差方法,能有效提高全空间辐射场计算效率。

基于粒子通量的GVR方法的权窗下限可表示为

(1)

其中:Φi为第i个栅元/网格内粒子的平均注量;Max(Φi)为所有栅元/网格中最大粒子平均注量;β为栅元/网格权窗上限下限之比。

引入体积修正后的权窗下限可表示为

(2)

其中:Vi为第i个栅元/网格的体积;Vs为点源所在的栅元/网格的体积。

非计数区内模拟粒子只有输运至计数区才能对计数区粒子注量有贡献。非计数区栅元/网格内粒子输运至计数区栅元/网格的概率为e-s/λ(s为非计数区栅元/网格到计数区栅元/网格的距离,λ为粒子的平均吸收自由程)。引入非计数区修正后的非计数区的权窗下限可表示为

wth,nonc=wth,nes/λ

(3)

其中:wth,nonc为非计数区栅元/网格的权窗下限;wth,n为离非计数区最近的计数区栅元/网格的权窗下限。

图10为全局减方差方法流程图。具体步骤为:(1)首先建立辐射场输运计算模型,采用蒙特卡罗方法跟踪辐射场中模拟粒子的输运过程,并统计计算所有栅元/网格内粒子信息;(2)根据粒子信息计算全局减方差方法的权窗参数,对权窗参数进行体积修正和非计数区修正;(3)采用修正后的权窗参数,跟踪模拟粒子在权窗引导下的输运过程,并统计计算所有栅元/网格内粒子信息;(4)判断计算得到粒子信息的相对偏差是否收敛,如未收敛,则返回步骤(2)迭代,直到收敛。

采用直接模拟和修正后的GVR方法模拟计算了爆高为20 m,高度为0～1 km,水平距离为5 km范围内γ射线注量。两次模拟的CPU总运行时间都设置为400 min。图11直接模拟和修正后的GVR方法计算γ注量相对偏差的分布。由图11可见,直接模拟得到大空间辐射场的平均相对偏差为20%,最大为100%;修正后的GVR方法模拟迭代3次得到的大空间辐射场平均相对偏差为1.2%,最大为4.2%,与直接模拟相比,平均相对偏差降低一个量级以上。

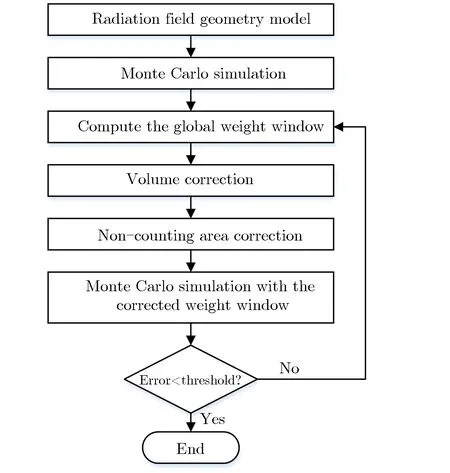
图10 全局减方差流程图Fig.10 Flow chart of the corrected GRV method

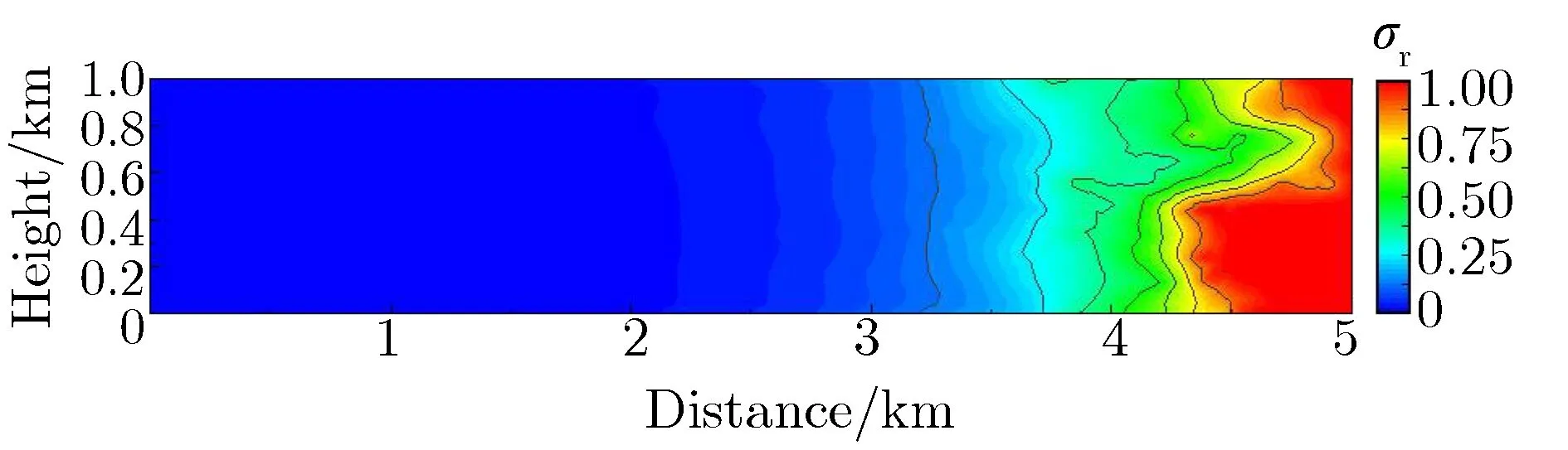
(a) Direct simulation

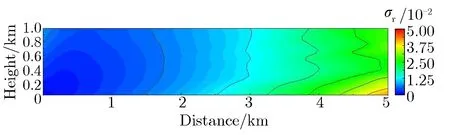
(b) GVR

2 蒙特卡罗方法在高空核爆炸辐射环境模拟中的应用与发展

按照时间尺度,可将高空核爆炸产生的辐射环境,分为瞬时辐射环境与长期辐射环境,蒙特卡罗粒子输运方法在高空核爆炸辐射环境的计算中也有广泛运用。

2.1 裸核区效应

X射线是一种光子,和源自核过程的γ射线不同,X射线主要来自于核外电子的跃迁[1],因此,能量低于γ射线,但又显著高于可见光。一般而言,X射线的波长主要集中在0.01 ～10 nm之间[23]。对应的单光子能量约为0.145～124 keV。X射线的能量远小于电子对效应的反应阈值,因此X射线和物质的主要相互作用为光电离效应和康普顿效应[24]。核爆炸中的X射线主要来自于高温等离子体的辐射复合过程。核爆炸火球的初始温度高达数千万开甚至更高,且处于热平衡状态[25]。可视作一个黑体[16]。因此,可用一个或多个黑体谱的组合来表征核爆炸X射线的能谱。

X射线的环境参数主要包括X射线的能注量和能谱。能注量是指通过空间中某一点单位面积上的能量。可以证明,对于包含散射作用的物理过程,在经过一定距离的输运后,已发生散射的粒子的比例会上升并成为主要成分。对于X射线来说,当单光子能量约为30 keV时,光电吸收截面和康普顿截面近似相等。因此,对于较硬的核爆炸X射线源,输运时散射效应非常明显。故X射线的输运过程常用蒙特卡罗方法进行模拟。X射线的模拟需要注意3个问题:一是长距离输运时的方差控制;二是垂直大气结构的精确表征;三是非稀薄介质中的近场裸核区效应。

对于长距离输运的方差控制问题,可使用权窗和源偏倚的方法削减方差随距离增加的趋势。通过多次迭代,反复优化空间中的权窗分布和源的偏倚设置,可实现较长距离的输运,同时保持较低的方差水平。

对于大气垂直结构表征问题,引入国际标准大气模型[26],建立了一套可考虑不同经纬度、海拔(0～1 000 km)、季节及太阳辐射强度的大气组分计算程序,可在蒙特卡罗输运中较准确地描述介质属性。大气组分的垂直分布如图12所示。

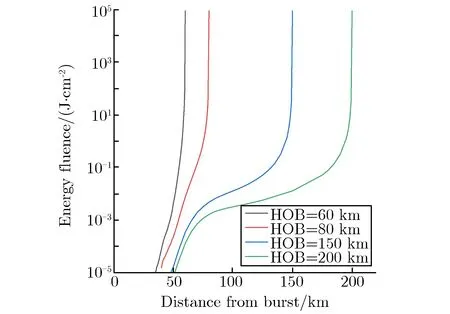
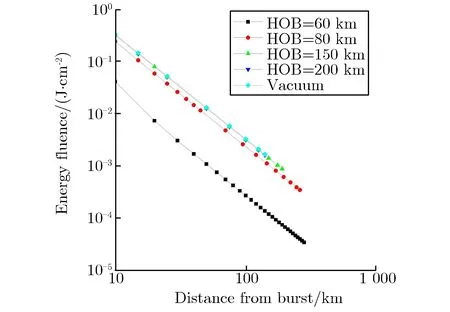
在非稀薄介质中的近场输运中,裸核区现象对X射线环境参数的影响较大。对于这一问题,基于独立原子近似[27]和壳层电离模型[28]开发了裸核区数值计算程序[29],能给出不同爆炸场景下的裸核区参数[30],包括裸核区大小、沉积在裸核区中的能量份额及裸核区边界能谱。通过以上方法,实现了大气层内核爆炸X射线环境的模拟计算功能。爆高不同时,高空核爆炸X射线能注量ΨX模拟计算结果如图13所示。

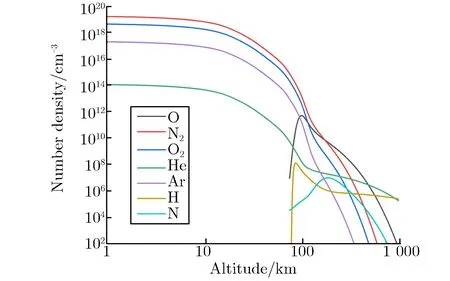
图12 大气组分的垂直分布Fig.12 Vertical distribution of atmosphere components

(a) Downward direction

(b) Upward direction

通过大量计算,得到了大气层内核爆炸X射线环境的一些基本规律:对于爆炸高度在50 km以上的场景,X射线在向下传输时存在一个截止高度,对于不同能量的X射线,这个值为20～50 km,X射线在这一高度层几乎全部沉积,无法向下穿透;对于爆炸高度在50 km以下的场景,X射线注量随着爆心距的增加快速下降,其本身的作用效果(这里不包含由X射线引发的电磁脉冲等其他间接效应)范围较为有限,一般在千米量级;对于150 km及以上高度的核爆炸,往往可以使用简单的平方衰减率近似估算其能注量。

2.2 附加电离源建模及其在非均匀大气中的输运

高空核爆炸产生的瞬发辐射(中子、γ和X射线)和缓发辐射(γ射线和β粒子)会电离高空大气,造成电离层电子数密度剧增,形成所谓的“附加电离层”,从而破坏无线电通信、雷达等系统的通信链路。附加电离层模拟的难点技术问题之一就是电离源建模及其在非均匀大气中输运的蒙特卡罗模拟。

瞬发中子、γ和X射线在爆炸瞬间释放出来,可视为各项同性的点源。缓发γ射线和β粒子则由裂变产物形成的碎片云持续释放,辐射源是一个时间空间持续变化的体源。当爆炸高度和当量不同时,碎片云形状可由球形演化为扁椭球形或倒梨形等,可采用流体力学模型描述碎片云的时空演化过程[31-32],计算得到碎片云运动参数。针对碎片云形状随时间不断演化特性,采用辐射源分层抽样的方法得到缓发γ射线的初始位置。根据不同时刻的碎片云高度和几何形状,将碎片云等份额划分为多层,每层等效为一定高度上均匀分布的薄圆柱体,倒梨形碎片云形成的缓发γ射线源如图14所示。通过分层均匀抽样实现对不规则体源的抽样。

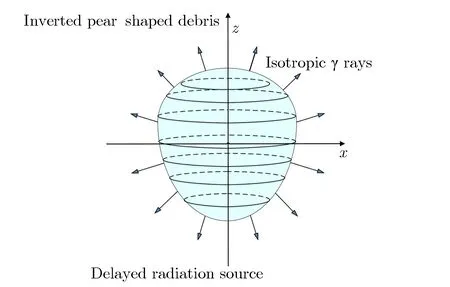
图14 倒梨形碎片云形成的缓发γ射线源Fig.14 The delayed γ-ray source from the inverted pear-shaped debris

由于高空大气密度随高度增加而指数衰减,传统蒙特卡罗方法要实现步长抽样,只能将高空大气分层处理,划分为内部密度均匀的密集薄层。每层大气厚度越小,计算结果越精确,同时计算量也越大。本文建立了基于质量厚度抽样的蒙特卡罗方法,在粒子输运过程中,对两次碰撞点之间的空气质量厚度进行抽样,再将质量厚度转换为每一步的步长。质量厚度抽样代替步长抽样,无须对高空大气进行分层处理,可简化大气几何模型,提高蒙特卡罗方法计算效率。采用该方法建立了中子、光子在高空大气中输运的专用蒙特卡罗程序MCATNP[33]。图15为MCNP和MCATNP程序计算给出的X、γ和中子能注量随距离的变化关系。其中,计算场景爆高取为100 km,当量取为1 Mt TNT,X射线能谱采用黑体温度为1.5 keV的普朗克谱,γ射线和中子能谱分别采用氢弹出壳γ射线和中子的能谱[8]。由图15可见,X、γ和中子能注量均随距离的增大成指数衰减关系,且MCATNP模拟结果与MCNP结果吻合得较好,表明质量厚度抽样方法可用于计算高空核爆炸产生的X、γ和中子能注量。

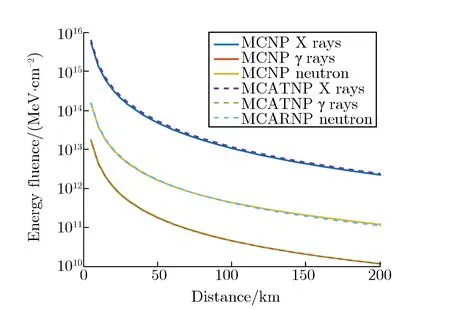
图15 MCNP和MCATNP程序计算给出的X、γ和中子能注量随距离的变化关系Fig.15 The X, γ and neutron energy fluences vs. distance computed by MCNP and MCATNP

基于碎片云运动参数和裂变产物设置电离源,采用基于质量厚度抽样的蒙特卡罗方法跟踪模拟瞬发辐射和缓发γ辐射电离大气分布,结合缓发β粒子电离大气分布数值求解电离连续性方程组,进而得到高空核爆炸电离大气产生的附加电离层环境。爆高为50 km,当量为50 kt TNT,爆后5 min电离层电子数密度的分布如图16所示。由图16可见,最高处比背景电离层高出3～4个量级。

图16 爆高为50 km,当量为50 kt TNT,爆后5 min电离层电子数密度的分布Fig.16 The electron number density distribution at 5 min with the detonation height of 50 km and the yield of 50 kt TNT

2.3 基于蒙特卡罗与带电粒子推进相结合方法的人工辐射带数值模拟

高空核爆炸裂变碎片在运动过程中衰变产生的β电子被地磁场捕获注入到自然辐射带中,形成人工辐射带。人工辐射带能覆盖全球、电子注量率高、持续时间长,会对卫星等空间目标产生总剂量和充放电等多种破坏效应。核爆炸释放带电粒子注入辐射带的过程可采用基于蒙特卡罗与带电粒子推进相结合[16]的方法,通过跟踪核爆炸主要裂变衰变链碎片离子在地磁场和大气作用下的运动,统计获取碎片离子和衰变β电子的捕获效率及爆后初始电子注量率随经度、磁壳参数、能量及赤道倾角余弦的分布。

核爆炸裂变产物有近千种放射性同位素,不同中子能量诱发裂变材料裂变产额不同。为简化计算,选取总产额较高的质量链并整理构建裂变产物数据库,包括所选取质量链的总产额及各质量链中考虑核素的质量数、质子数、独立产额及半衰期等参数。

在构建高空核爆炸后初始碎片离子的空间、速度及方向分布模型的基础上,采用随机蒙特卡罗抽样方法,确定碎片离子的初始位置;采用Boris推进方法跟踪碎片离子在地磁场和大气作用下的运动[34];采用寿命概率模型结合裂变产物数据库进行随机抽样,确定放射性碎片发生β衰变的时刻和位置,并根据裂变衰变β电子能谱抽取电子能量。模拟过程中如裂变产物发生β衰变,根据裂变衰变质量链,裂变碎片采用新的子体,其速度和位置仍用母体的速度和位置,继续跟踪裂变碎片直到其子体为稳态核或能量小于截断能量。

根据上述方法通过跟踪大量碎片离子的运动,得到裂变衰变β电子的位置、能量和方向,进而计算爆后初期赤道面电子注量率分布。在此基础上,结合辐射带电子长期扩散损失模拟方法,实现了高空核爆炸人工辐射带环境参数的数值模拟。爆高为400 km,当量1.4 Mt核爆炸的初始捕获电子数Ne随磁壳参数L的分布和电子全向注量率φe随时间t的变化关系如图17所示。由图17(a)可见,初始捕获电子随磁壳参数的分布并不是以爆心为中心,而是在高L值上的分布占多,这是由于碎片离子的径向扩散使其向更高方向运动;由图17(b)可见,电子注量率随时间近似成指数形式衰减关系,衰减到本底需2～3 a。

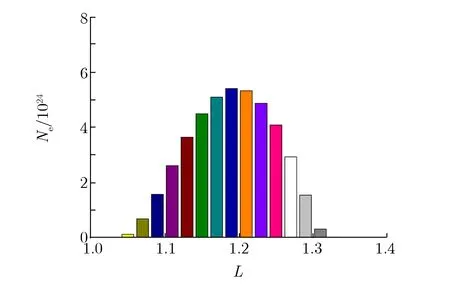
(a) Ne vs. L

(b) φe vs. t

2.4 基于蒙特卡罗模拟的高空核电磁脉冲源项计算方法

高空核电磁脉冲按照产生机理分为早期(E1)、中期(E2)和晚期(E3)电磁脉冲。直达γ、散射γ和中子次级γ射线是产生E1和E2的主要因素。在以往的E1模拟中,往往直接采用解析公式计算直达γ注量作为辐射源项,忽略了散射γ射线的影响,也忽略了γ射线时间谱、能谱和角度谱特性。E2的主要辐射源项为中子次级γ射线,目前尚无解析公式可计算其注量。因此,本文提出了基于蒙特卡罗模拟的高空核电磁脉冲源项计算方法,通过跟踪模拟核爆炸γ射线和中子在高空非均匀大气中的输运过程,获得E1和E2的源项参数。

向下传播的γ射线在距地面20～40 km高度形成沉积区,激励产生电磁脉冲。核爆炸γ射线和中子由爆点输运至沉积区的蒙特卡罗模拟面临深穿透问题。图18为γ射线和中子在高空大气中输运的几何模型示意图。由于计算空间尺度长达数百千米,且高空大气不断与γ射线和中子发生吸收和散射作用,直接蒙特卡罗模拟时,到达记录点(尤其是高度为20 km的记录点)附近的模拟粒子极少,使蒙特卡罗模拟的统计涨落较大,模拟结果不可信。必须采用源偏倚、几何分裂和时间分裂等综合减方差技术[35],提高计算效率与计算精度。爆高为80 km、当量为1 Mt TNT核爆炸情况下,高度为20 km处的不同组成和方向的γ注量率φγ随时间的变化关系如图19所示。由图19(a)可见,1 μs之前,直达γ射线占主导;1～100 μs,散射γ射线占主导;100 μs后,中子次级γ射线占主导。

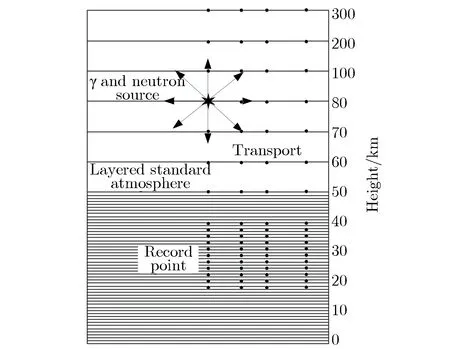
图18 γ射线和中子在高空大气中输运的几何模型示意图Fig.18 The sketch of the geometry model of γ-rays and neutron transport in the upper atmosphere

粒子的角分布是高空核电磁脉冲源项的关键参数之一。蒙特卡罗模拟中常见的基于面计数的角分布统计方法仅适用于面流量记录方式,难以给出满足电磁脉冲计算精度的粒子角分布。本文提出了基于点通量记录的粒子角分布计算方法。在点通量记录中,设置参考方向,计算虚粒子的方向与参考方向的夹角,并根据夹角统计计算不同角度分区内的粒子注量。由图19(b)可见,在1 μs以前,直达γ射线占主导地位,γ射线方向几乎均沿r方向;1 μs之后,由于散射γ和中子次级γ方向分布的复杂性,γ射线沿各方向分量均有分布。

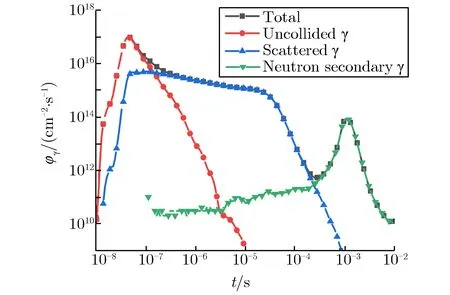
(a) Composition

(b) Direction

HEMP模拟计算时所需求的最直接的参数就是康普顿电子信息。前人的研究中往往根据γ射线注量率、能量来计算康普顿电子参数,忽略了随时间变化的γ射线能量分布和角分布。本文通过在点通量记录中构造基于康普顿散射理论的探测器响应函数,直接统计计算康普顿电子的产生率,同时利用康普顿散射理论计算康普顿电子的数量、能量和方向等信息,最后根据康普顿电子产生率和能量方向信息计算得到初始康普顿电流密度。该方法直接由蒙特卡罗模拟给出初始康普顿电子信息,可考虑γ射线和康普顿电子的时间、能量和方向等影响因素。

根据蒙特卡罗模拟计算的康普顿电子信息,计算得到初始康普顿电流和传导电流,代入麦克斯韦方程组,求解得到电磁脉冲波形与电场强度[36]。图20为不同辐射源项产生的电场波形。由图20可见,电场波形明显具有直达γ、散射γ和中子次级γ射线的特征;直达γ射线引起早期E1快速上升的电场强度峰值,最大峰值约为50 kV·m-1;散射γ射线在1 ～100 μs占主导地位,对应峰值电场强度可达100 V·m-1;中子次级γ射线在10-3～10-2s引起第二个峰,峰值电场强度约为10 V·m-1。

3 结论与展望

本文作者团队经长期持续研究,采用蒙特卡罗模拟方法,建立了大气层核爆炸与高空核爆炸诸多核辐射环境参数的数值模拟计算模型与方法。在大气层核爆炸方面,构建了冲击波影响下缓发γ辐射输运模型和大规模复杂城市条件下粒子输运模型,建立了权窗结合密度逼近迭代的减方差方法和GVR方法等一系列减方差方法,解决了核辐射在近地面大气远距离输运模拟的深穿透问题。在高空核爆炸方面,建立了考虑裸核区的X射线输运模型、附加电离源建模及其在非均匀大气中的输运模型、基于蒙特卡罗与带电粒子推进相结合的人工辐射带注入模型和基于蒙特卡罗模拟的高空核电磁脉冲源项计算方法,实现了高空核爆炸X射线、附加电离、人工辐射带和核电磁脉冲等辐射环境数值模拟。

核爆炸辐射环境涉及因素多,机制机理复杂,空间尺度大,时间跨度大,在数值模拟方面存在较多需要进一步研究解决的问题。在核爆炸辐射环境计算中,某些计算模型过于简单,气象条件、地形地貌和建筑物类型等实际复杂因素考虑不充分不全面。在蒙特卡罗模拟中,为解决远距离输运带来的深穿透问题,建立了相应的减方差方法提高计算效率与精度,但一旦变换场景条件相关的参数,需重新迭代计算权窗等参数,耗费大量时间。

下一步将梳理总结大气层和高空核爆炸核辐射环境模拟中的建模方法和蒙特卡罗减方差方法,建立一系列核辐射环境参数计算的标准规范,开发自主专用的核辐射环境数值模拟程序,切实提高核辐射环境数值模拟能力。