爆炸容器研究进展

2023-10-20刘文祥张德志马艳军

现代应用物理 2023年3期

刘文祥,张德志,程帅,马艳军

(西北核技术研究所;强脉冲辐射环境模拟与效应全国重点实验室: 西安 710024)

爆炸容器是限制爆炸作用的一种特种装备,最早于1944年开始研制,可把爆炸冲击波、爆炸产物及高速飞片等限制在一定范围内,起到保护人员和设备、回收试验产物及防止环境污染等作用[1-5]。在工业和国防等领域,爆炸容器是爆炸加工、爆炸试验、火工品储存和转移及过期武器弹药销毁等过程的常用防护设备[6-12];在科研领域,爆炸容器是研究开展爆燃和爆炸相关研究的重要实验装备[13-19];在公共安全方面,车站、机场等公共场所常配备爆炸容器,以便紧急处理可疑的爆炸物品[20]。可见,爆炸容器已得到广泛应用。

爆炸容器涉及的主要物理过程是爆炸强动载与目标相互作用:爆炸产生的瞬态强冲击(作用时间可达到微秒量级,压力可达到吉帕量级)与容器壳体相互作用,容器发生高强度的动态响应(应变率最高可达102～103量级)。随着需求的增长,爆炸容器的研究日益受到关注。但爆炸容器问题理论上属于高度非线性的数学问题,在实验研究上涉及瞬态、强冲击、高温及强电磁等极端条件,在学科上涵盖了爆炸力学、冲击动力学、材料力学及机械设计与制造等多个领域,因此相关研究极具挑战性。

本文介绍了国内外爆炸容器研制、容器内载荷规律、容器动态响应及容器设计标准4个方面的现状及西北核技术研究所的研究进展。

1 国内外技术现状

1.1 容器种类和研制

通常爆炸容器按照结构特征进行分类,可分为球形容器、柱形容器和其他结构形式的容器;按照制作材料和工艺的不同,可分为钢制容器、纤维复合材料容器及扁平钢带缠绕式容器等;按照使用次数的多少,分为一次性使用和重复使用2类,其中一次性使用容器允许发生塑性变形,重复使用容器一般严格限制在弹性变形范围内。

20世纪90年代,美国Los Alamos国家实验室双轴闪光照相实验用容器如图1所示[13-15]。

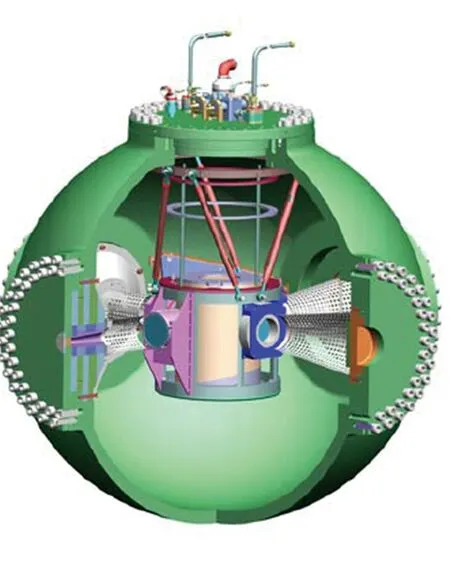
(a) Confinement vessel

(b) Safety vessel图1 美国双轴闪光照相实验用容器[13-15]Fig.1 Confinement vessel and safety vessel of DARHTF in US[13-15]

图1(a)为典型球形爆炸容器,用于确保有毒放射性物质在爆炸作用下的有效封闭,容器内径为1.83 m,采用HSLA-100钢,可承受24.2 kg TNT当量的爆炸,该容器属于一次性使用容器。苏联曾研制过1 000 kg TNT当量的球形爆炸容器[10],直径为12 m,壁厚为100 mm,质量约为350 t。1984年,章仕表等[19]制造了1 kg TNT当量爆炸容器。中国工程物理研究院胡八一等[20]研制了25 kg TNT当量可重复使用球形爆炸容器,内径为3.6 m,采用BHW35钢,壁厚为90 mm。胡八一等[21]还研制了1 kg TNT当量球形爆炸容器,内径为1 m,壁厚为25 mm,采用16MnR钢,容器正上方开设直径为125 mm的装药孔,赤道面上开设直径为80 mm的定位孔,正下方有直径为25 mm的排污孔。

柱形是爆炸容器另一种常用的结构。美国Los Alamos国家实验室[13-15]在双轴闪光照相实验中,球形爆炸容器外套了带椭圆封头的柱形容器,如图1(b)所示,内径为2.44 m,同样使用HSLA-100钢。美国Esparza等[22]研制了能承受10 kg TNT当量的柱形容器,容器直径为3.5 m,厚为38.1 mm,椭圆封头厚为51 mm,采用HY100钢。日本神户钢铁公司采用爆炸法销毁非库存化学武器,为此研制了15 ,45,60 kg TNT当量系列柱形爆炸容器[12],采用双层结构,内层容器承受爆炸冲击波和破片侵彻作用,外层容器承担准静态气压。宋桂飞等[11]研制的一种回收战斗部破片的爆炸容器,内径为1 200 mm,壁厚为36 mm,容积为2.08 m3,材料为16MnR钢,内衬防护板为616装甲钢板;上端开口,底部注入深360 mm的水。国防科技大学曹胜光等[23]研制了5 kg TNT当量柱形爆炸容器,筒体内径为2 800 mm,圆柱形筒体长为4 500 mm,容器壁厚为45 mm,采用16MnR 钢制造。

为满足一些特殊需求,爆炸容器还采用一些新型材料或结构形式。美国Livermore国家实验室为满足在“先进流体动力学设施”中使用无窗口容器的需求,Pastrnak等[9,18]研制了Kevlar纤维缠绕球形爆炸容器,容器由外向内依次为强度层(Kevlar纤维缠绕层)、密封层(铝合金内衬)和防弹层(陶瓷),容器直径为2 m,设计爆炸当量约为35 kg TNT。胡八一等[24]研制了树脂基玻璃纤维复合材料球形和柱形爆炸容器,内径均为500 mm,分别安全承受了当量为1.8,1.5 kg TNT的爆炸。浙江大学郑津洋团队[25-27]开展了离散多层爆炸容器抗爆性能研究,离散多层爆炸容器是扁平绕带式压力容器的应用拓展。

1.2 容器内爆炸载荷

爆炸冲击波在容器内壁反射形成很强的冲击载荷。美国军事部门发布的TM 5-1300手册[28]给出了TNT装药空中爆炸冲击波正反射参数的经验图,参数包括超压峰值和比冲量,比距离为0.15～100 m·kg-1/3。这些数据可用于爆炸容器内载荷计算。Baker等[29]曾汇总了多位学者的研究数据,总结出正反射超压峰值、比冲量与比距离关系的经验图,超压峰值数据比距离为0.2～104m·kg-1/3,比冲量数据的比距离为0.1～104m·kg-1/3。对于非TNT炸药,可通过爆炸释放的热能等效转化为TNT炸药[30-32]。由于比距离小于0.2 m·kg-1/3的爆炸实验开展得较少,上述文献中列举的比距离小于0.2 m·kg-1/3的爆炸冲击波参数,一般是通过两种方法获得的:一是理论和数值计算;二是通过低环境气压爆炸实验由Sachs比例定律推算而得。

爆炸容器内部载荷属于约束爆炸载荷,冲击波在容器内壁来回反射,因此,此类载荷具有一定的周期性特征。图2为球形容器内壁载荷波形。

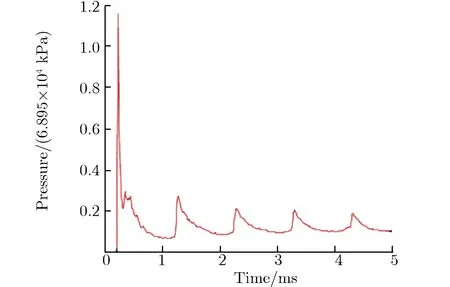
(a) Numerical result

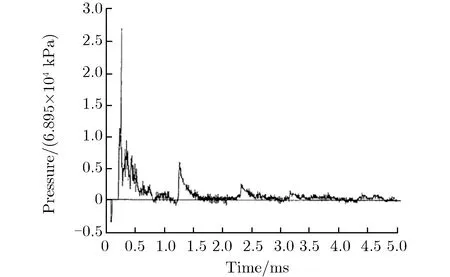
(b) Experimental result图2 球形容器内壁载荷波形Fig.2 Load on the inner wall of spherical vessel

Duffey等[33]通过数值模拟给出了球形容器内的周期性载荷波形,包括一个较强的首脉冲及多个较弱的后续脉冲,如图2(a)所示。Dong等[34]通过数值模拟研究了爆炸载荷与球壳相互作用过程,并把球壳内的载荷分为初始冲击波阶段、冲击波反射阶段和压力振动阶段。初始冲击波阶段是指初始冲击波作用在容器上的阶段;冲击波反射阶段是指冲击波在容器壁和容器中心来回反射的阶段;压力振荡阶段是指容器内冲击波衰减消失,但容器振动没有停止,容器体积的周期性变化导致气体压力周期性微小变化的阶段。段卓平等[35]采用2维欧拉有限差分程序计算了柱形容器的内部爆炸流场,爆炸产物和空气都采用理想气体状态方程,结果表明,容器内载荷存在多次脉冲。Lewis等[13]通过实验获得的球形容器内壁载荷波形,如图2(b)所示,由图2(b)可见,曲线中仅存在3个比较显著的脉冲(数值模拟显示存在大量的脉冲),之后压力变化比较平缓,容器内气体进入准静态压力状态,但该研究的可用数据点不多,也没有给出各个脉冲关键参数的规律。综上,周期性特征是容器内载荷普遍特征,但数值模拟在模拟这一特征时与实验结果还存在明显差异。

周期性载荷之后爆炸容器内压力为准静态。一般认为,准静态压力P与爆炸当量Q跟容器容积V的比Q/V成线性正比关系[15,36]。Marchand等[37]给出了4种炸药爆炸的准静态压力P与Q/V之间的关系,发现富氧炸药和负氧炸药存在差异。其中,富氧炸药RDX的准静态压力与Q/V基本成线性关系;而其他富氧炸药的准静态压力与Q/V的关系偏离了线性关系,当Q/V较小,容器内氧含量相对较多时,准静态压力高于RDX,当Q/V较大,容器内氧含量相对较少时,准静态压力明显低于RDX。

1.3 爆炸容器动态响应

1958年,Baker等[38-39]推导了薄球壳在弹性变形范围内的1维线性方程,之后进一步假设材料模型为双线性弹塑性模型,推导出容器发生塑性变形的1维线性方程,并进一步考虑容器壁厚的变化,推导得到塑性响应非线性方程,还通过数值方法进行求解。Duffey等[33]基于球壳响应理论研究了弹性变形范围内壳体变形随爆炸载荷作用时间和结构振动周期之比的变化关系。Ivanov等[40]总结了6个球形容器和2个柱形容器的实验研究工作,通过在同一容器中反复进行多次的同当量爆炸加载,发现容器材料发生明显强化,并得出与静态屈服强度相比,第一次加载时的材料动态屈服强度增强了40%,分析认为是应变率效应的作用。Duffey等[41]和Benham等[42]对柱壳的环面变形进行了理论分析,利用经验公式得到柱壳内爆炸载荷的比冲量分布规律,再假设爆炸载荷对柱壳做的功与容器内部应力所做的功相等,进而计算柱壳的环面变形,分析结果与实验吻合。White等[43]总结了以前的爆炸容器工作,发现应变率效应导致容器材料屈服强度增加,还从能量角度分析得到,允许发生塑性变形的容器的重量为仅发生弹性变形的容器重量的1/5～1/35。王礼立等[44]研究了球形爆炸容器的动态断裂问题。

应变增长现象是指容器壳体的最大变形不出现在第一个变形周期,而出现在之后周期的现象。1976年,Buzukov[45]在柱形壳体爆炸加载实验中首次发现该现象,出现时容器内载荷已衰减,分析认为该现象由容器不同模态的振动叠加形成。Abakumov等[46]利用Timoshenko理论对爆炸加载下的球壳响应进行数值求解,发现容器赤道附近没有应变增长现象,而在容器极点(开口的正对位置)处应变增长现象非常显著,分析认为容器的非理想球形结构致使壳体弯曲振动被激发,弯曲振动在传播的过程中振幅不断增大。Belov等[47-48]研究球壳响应时,认为应变增长现象并非由载荷与壳体振动之间的“共振”产生,而是由壳体振动叠加而形成。Karpp等[49]针对球形容器的爆炸加载实验,推测弯曲振动起源于法兰,并在极点处汇聚,导致极点处出现严重的应变增长现象。Kornev等[50]认为柱形爆炸容器法兰附近存在着强烈的弯曲振动,弯曲振动与频率相近的其他振动叠加形成应变增长现象。朱文辉等[51]针对柱形容器,推测频率相近的振动叠加形成了应变增长现象,还提出通过控制柱形容器的尺寸来抑制应变增长现象。前面文献主要判断振动叠加是应变增长现象形成原因,Duffey等[52]首次解释了振动叠加是如何形成应变增长现象的,利用频率相近的振动叠加形成的“拍”现象来解析应变增长现象,并通过对比实测应变波形的频率、“拍”的频率,验证关于“拍”的假设的合理性。图3为“拍”形成的示意图。

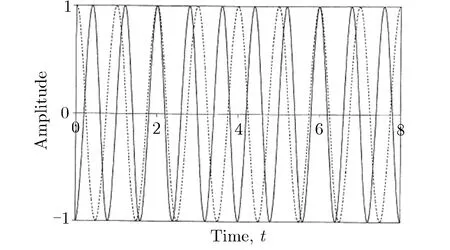
(a) Before superposition

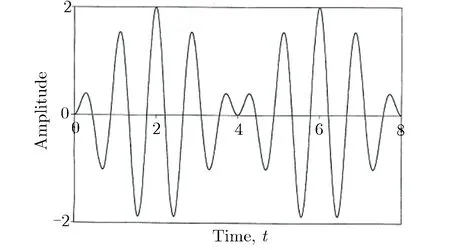
(b) After superposition图3 “拍”形成的示意图Fig.3 Diagram of beating

Dong和Li等[53-54]开展系列柱壳、球壳等应变增长现象的数值模拟,并基于Mathieu方程分析了壳体振动特征,提出非线性模态耦合叠加可能是应变增长现象产生的一种重要原因,并提出选择合适的容器厚度和半径之比,减少第一个应变峰值,可抑制应变增长现象,容器设计应考虑应变增长现象。

容器内周期性载荷与壳体振动“共振”是应变增长现象形成的另一个原因。Buzukov等[55]研究柱形容器应变增长现象时,认为壳体内周期性载荷是应变增长现象出现的原因之一。Karpp等[49]研究发现周期性爆炸载荷对球壳响应具有显著影响。Kornev等[50]利用数值模拟研究爆炸加载下的球壳响应,认为当壳体振动周期是载荷周期的整数倍时会发生“共振”,有可能导致后续应变大于第一个周期。Duffey等[33]在分析球形容器的应变增长现象时,认为容器内周期性的载荷也可能是应变增长现象形成的一个原因。Dong等[34]借助数值模拟较详细地分析了爆炸载荷与壳体振动”共振”引起的应变增长现象,发现当爆炸载荷的周期与壳体振动周期接近时,“共振”可能导致较显著的应变增长现象,且应变增长系数与炸药半径和容器半径之比有很大关系。

1.4 容器设计标准

Duffey等[56]认为爆炸容器设计可部分参考ASME锅炉与压力容器设计标准,但ASME标准的适用范围限于爆炸后长时间的准静态压力载荷。中国工程物理研究院胡八一等[57]总结近30年的容器设计和试验工作,提出了一种基于动力系数法的爆炸容器的设计方法。廖英强等[58]采用类似的思路提出了复合材料爆炸容器的设计方法。段卓平等[35]针对突发事故爆炸容器,针对多次相同加载的特殊情况,将壳体材料简化为线性硬化材料,提出了壳体多次变形累积起来变形达到极限状态进而失效的容器寿命估计方法。

2 西北核技术研究所爆炸容器的研究进展

20世纪90年代,西北核技术研究所[59-61]建立了10 kg TNT立式柱形爆炸容器,属于可重复使用容器,由两个椭球封头和一段圆柱形筒体用螺栓联接组合而成,内径为2.182 m,壁厚为65 mm,圆柱段高为2 m,封头由标准椭球封头壳和高度为0.5 m的圆柱筒焊制。之后,重点围绕一次性使用的柱形和球形爆炸容器开展研究,获得的主要成果为:

(1)较系统地研究了柱形和球形爆炸容器内载荷规律,特别是实验获取了比距离小至0.1 m·kg-1/3容器内壁冲击波数据和球形容器内周期性载荷数据。林俊德[62]对各种经验公式和图表进行了综合分析和比较,给出了比距离为0.2～3 m·kg-1/3范围内的冲击波入射超压峰值、正反射超压峰值、正作用时间和比冲量的计算公式。张德志等[63-64]在直径为200 mm的柱形容器中,利用行波杆测量容器内壁的冲击波正反射载荷,并通过拟合实验数据得到超压峰值和比冲量的经验公式,比距离最小达0.1 m·kg-1/3,小比距离下容器内壁正反射爆炸载荷如图4所示。

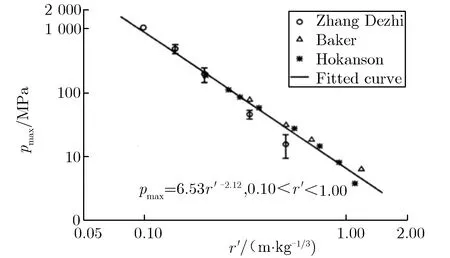
(a) Pressure peak

(b) Specific impulse图4 小比距离下容器内壁正反射爆炸载荷Fig.4 Reflection load on the inner wall of vessel specific within a small specific distance range

对于爆炸容器内非球形炸药,通常通过体积相等转化为球形炸药进行处理,但比距离较小时,装药形状的影响不可忽略。林俊德[62]、张德志等[63-64]、刘文祥等[65]在柱形容器内通过实验和数值模拟发现,等长径比圆柱形装药在径向方向的超压峰值、比冲量比相同质量球形装药高出约1倍。刘文祥[66]实验测得了丰富的球形容器内周期性载荷数据,比距离为0.36～0.87 m·kg-1/3,并建立了周期性爆炸载荷的简化模型,并通过总结实验数据,得到各脉冲的持续时间、超压峰值、比冲量的经验图表或公式。陈勇军[27]、王等旺等[67]在柱形容器内开展了准静态压力的实验研究,获得了准静态压力随Q/V的变化关系;刘文祥等[68]总结球形了爆炸容器内准静态压力的经验公式。

(2)较系统地研究了柱壳、球壳弹塑性变形响应规律。钟方平等[69]研究了双层柱形爆炸容器弹塑性结构响应,发现炸药量相同,采用双层结构时,外罐体变形远小于单层结构的变形,内层罐承担了很大的冲击载荷,很好地保护了外罐;在相同药量和罐体结构条件下,抽真空后罐体应变峰值约为不抽真空情况的50%～80%。王等旺等[67]研究了单层柱壳在球形集中装药作用下的塑性变形及分布与壳体几何结构、材料参数和装药量的关系,给出了相应的经验计算公式,发现等厚度柱壳的塑性变形仅分布在沿轴向±2倍半径非常有限的范围内,呈高斯函数分布特征。刘文祥[66]基于实验获取了容器内壁周期性载荷数据,借助球壳响应理论,分析了单个脉冲球壳的弹塑性响应,得到了球壳的应变峰值随比冲量、载荷持续时间的变化关系,还分析了多个脉冲下球壳的弹塑性响应(即共振引起的应变增长现象),认为球壳弹性变形时最大应变增长系数为1.5,球壳发生较大塑性变形时最大应变增长系数为1.25,球壳发生较小塑性变形时最大应变增长系数为1.25～1.5。

(3)对振动叠加形成的应变增长现象进行解剖式研究。刘文祥等[66,69-73]提出了提取壳体膜应变和弯曲应变的方法,并从膜应变和弯曲应变的角度对球壳振动叠加形成的应变增长现象进行解剖式研究,进而直接观察到弯曲应变从扰动源产生、传播和汇聚、与膜应变叠加形成应变增长现象的全过程。图5为应变曲线被解剖成的膜应变和弯曲应变曲线。相关结论和成果有:呼吸振动和频率相近的弯曲振动叠加是应变增长现象形成的主要原因;由于弯曲波在扰动源正对位置的汇聚,导致该位置的应变增长现象是整个球壳最严重的;由于入射弯曲波和反射弯曲的叠加形成的“驻波”,应变增长系数在球壳上的分布成空间周期性;提出了抑制应变增长现象的新措施,包括避免扰动源被完全约束、减少扰动源尺寸和质量、对称设置扰动源等;首次观察到应变增长现象导致容器发生塑性变形及容器塑性变形下发生应变增长现象。

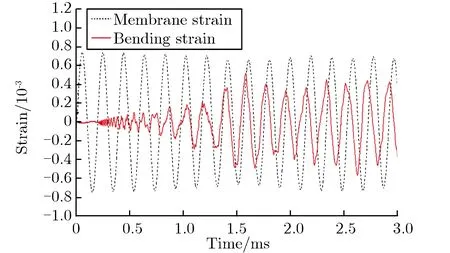
(a) Total strain curves

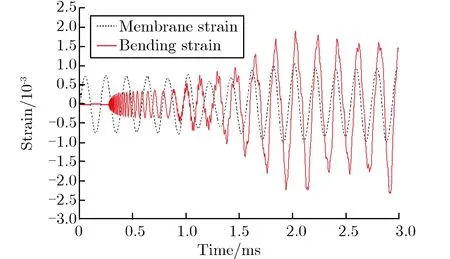
(b) Substrain curves图5 应变曲线被解剖成膜应变和弯曲应变曲线Fig.5 Total strain and sub-strain curves of spherical shell

(4)制定了爆炸容器的相关设计方案。程帅等[74-75]对球形容器开孔处等效应变随接管壁厚、补强圈尺寸的变化关系进行了研究,确定了“5/3倍球壳厚度的接管“配合”与球壳等厚度、张角为10°的补强圈”的开孔补强设计方案;还给出了爆炸容器端盖法兰结构的螺栓预紧力设计方法,发现由预紧力和脉冲载荷引起的螺栓总拉伸应变随载荷峰值变化的曲线上存在最小极值点,并总结了最小极值点随载荷峰值和载荷脉宽的变化关系。