一维带限Weierstrass分形粗糙面电磁散射的微扰法研究

孙 乐，任新成，田 炜，牛文军

（延安大学物理与电子信息学院，陕西延安716000）

一维带限Weierstrass分形粗糙面电磁散射的微扰法研究

孙 乐，任新成*，田 炜，牛文军

（延安大学物理与电子信息学院，陕西延安716000）

运用微扰法研究了平面波入射粗糙面的电磁散射问题。采用一维Weierstrass分形粗糙面模拟实际的粗糙面，结合其功率谱密度导出了散射系数计算公式；通过数值计算得到HH极化状态下散射系数的角分布曲线，讨论了分维、标度区间、空间基频、粗糙面高度起伏均方根以及入射波频率的变化对散射系数的影响；得到了平面波入射一维带限Weierstrass分形粗糙面散射系数的分形特征、基本特征、分区特征和随频率变化的特征。

电磁散射；一维带限Weierstrass分形粗糙面；微扰法；散射系数

粗糙面电磁散射是一个有着大量实际应用且为多学科领域共同研究的热门课题，从原子物理、医学成像、地球科学到遥感等都有粗糙面电磁散射的应用［1－7］。当两种均匀介质的交界面不规则时，只有交界面上散射单元的大小较入射波长小得多或者大得多的时候，才可以运用Kirchhoff近似（KA）［8］、微扰法（SPM）［9］和双尺度理论（TS）［10］等得出近似解析解。

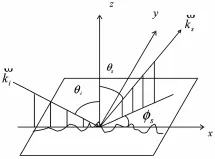
图1 粗糙面电磁散射几何示意图

1 微扰法理论

如图1所示为粗糙面电磁散射的几何示意图。若粗糙面统计参数满足微扰法的条件，即kδ＜0.32，21／2δ／l＜0.3，其中k为入射电磁波波数、δ为粗糙面高度起伏均方根，l为粗糙面高度起伏相关长度，则应用矢量场的一阶近似理论可以导出单位照射面积的非相干散射截面为［11］

2 一维带限Weierstrass分形粗糙面模型及其散射系数

3 数值计算结果和讨论

3.1 分维等分形描述量对散射系数的影响

3.1.1 分维对散射系数的影响

取δ＝0.10／k，ε＝1.6，b＝1.01，N1＝0，N2＝9，分别取D＝1.1，D＝1.5，D＝1.9，研究分维D对散射系数σ的影响，计算结果如图2所示。

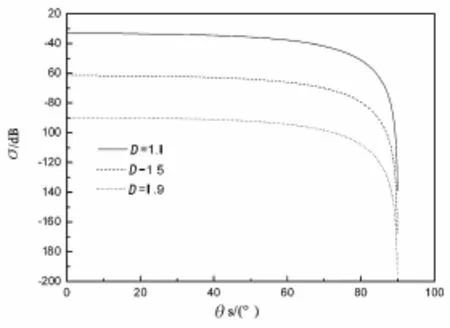
图2 分维对散射系数的影响

由图2可以看出，不同分维对应的曲线区别较为明显，分维对散射系数的影响比较大，在其他条件保持不变的情况下，分维越大，散射系数越小，总体上，散射系数随着散射角的增大而减小，减小的快慢随散射角的增大而增大，当散射角θs＞70°时，散射系数随着散射角的增大急剧减小。

3.1.2 标度区间N（谐波次数）对散射系数的影响

取δ＝0.10／k，ε＝1.6，b＝1.01，N1＝0，D＝1.5，分别取N2＝9，N2＝25，N2＝50，研究标度区间N对散射系数σ的影响，计算结果如图3所示。

从图3可以看出，不同的标度区间对应的曲线区别较大，标度区间对散射系数的影响比较大，在其他条件保持不变的情况下，标度区间N2越大，散射系数越小，总体上散射系数随着散射角的增大而减小，减小的快慢随散射角的增大而增大，当散射角θs＞70°时，散射系数随着散射角的增大急剧减小。

3.1.3 空间基频对散射系数的影响

取δ＝0.10／k，ε＝1.6，D＝1.5，N1＝0，N2＝9，分别取b＝1.01，b＝1.05，b＝1.10，研究空间基频b对散射系数σ的影响，计算结果如图4所示。

图3 标度区间N（谐波次数）对散射系数的影响

图4 空间基频对散射系数的影响

从图4可以看出，不同空间基频的大小对应的曲线区别较大，在其他条件保持不变的情况下，空间基频越大，散射系数越大，总体上散射系数随着散射角的增大而减小。

3.2 粗糙面高度起伏均方根对散射系数的影响

取ε＝1.6，D＝1.5，N1＝0，N2＝9，b＝1.01，分别取δ＝0.05／k，δ＝0.10／k，δ＝0.20／k，研究粗糙面度低起伏均方根δ对散射系数σ的影响，计算结果如图5所示。

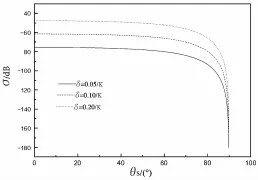
图5 粗糙面高度起伏均方根对散射系数的影响

从图5可以看出，不同δ对应的曲线区别是很明显的，在其他条件保持不变的情况下，粗糙面高度起伏均方根δ越大，σ就越大，总体上散射系数随着散射角的增大而减小。

4 散射系数的特征分析

根据上节中的数值计算结果，可以得到一维带限Weierstrass分形粗糙面散射系数的分形特征和基本特征。

4.1 分形特征

（1）分维对散射系数的影响很大，在其他条件保持不变的情况下，分维越大，散射系数越小，因此在使用分形粗糙面代替真实粗糙面时，一定需要注意选取合适的分维。

（2）标度区间N对散射系数的影响也比较大，在其他条件保持不变的情况下，标度区间N越大，散射系数就越小。

（3）空间基频对散射系数的影响比较明显，在其他条件保持不变的情况下，空间基频越大，散射系数越大。

4.2 基本特征

粗糙面高度起伏均方根对散射系数的影响比较大，在其他条件保持不变的情况下，高度起伏均方根越大，散射系数就越大。

4.3 分区特征

从图2～图5可以看出，散射系数随散射角变化的规律是很相似的，取其中之一并进行分区如图6所示。

图6 分区特征

从图6可以看出，散射系数随散射角的变化大致可以分为2个区域，Ⅰ区为缓变区，Ⅱ区为近平行平均平面散射区。在缓变区，散射系数随散射角的增大而减小，但减小得较慢；在近平行平均平面散射区，散射系数随散射角的增大而减小，但是减小得急剧。

4.4 随频率变化的特征

为了进一步研究散射系数σ随入射波频率f变化的特征，这里进行数值计算，图7给出了相应数值计算的结果，计算时各种参数的取值如下，ε＝1.6，D＝1.5，N1＝0，N2＝0，δ＝0.10／k，b＝1.01，分别取θs＝20°，θs＝80°。

图7 σ随f的变化

5 结束语

当平面电磁波入射到一分形粗糙面上时，发生在介质表面的电磁散射在诸多实际问题中有着广泛的应用。本文运用微扰法得到了平面电磁波入射到一维带限Weierstrass分形粗糙面上时散射系数的表达式，通过数值计算得到了一维带限Weierstrass分形粗糙面电磁散射的分形特征、基本特征、分区特征和随频率变化的特征。毫无疑问，这些结果在环境遥感、探地雷达、无线电传播与通信等电磁逆散射问题中有着广泛的应用。当然，这里只是研究了分维、空间基频、标度区间、粗糙面高度起伏均方根及入射波频率对一种比较简单的一维带限Weierstrass分形粗糙面HH极化散射系数的影响，对于其他谱分布以及更加复杂的粗糙面散射问题还有待进一步的研究。

［1］Ulaby T F，Moore R K，Fung A F.Microwave remote sensing［M］.London：Addision Wesbey Publishing，1982.

［2］Bass FG，Fuks IM.Wave scattering from statistically rough surfaces［M］.Oxford：Pergamon，1979.

［3］郭立新，柯熙政，吴振森.一维随机粗糙面电磁散射的小波矩量解［J］.西安电子科技大学学报，2000，75（5）：585－589.

［4］郭立新，吴振森.粗糙面散射物理光学近似条件中的曲率修正［J］.西安电子科技大学学报，2002，29（5）：245－248.

［5］郭立新，官秀国，徐英霞.分形粗糙面单站散射的遮蔽效应研究［J］.西安电子科技大学学报，2003，30（5）：617－622.

［6］郭立新，陈建军，韦国晖，等.粗糙面的电磁散射小斜率近似法研究［J］.西安电子科技大学学报，2005，32（3）：408－413.

［7］任新成，郭立新.一维带限Weierstrass分形粗糙面透射波散射系数特征研究［J］.西安电子科技大学学报，2007，34（4）：590－595.

［8］田炜，任新成.基于基尔霍夫驻留相位近似法的深粗糙度高斯型粗糙面光散射［J］.上海航天，2011，28（2）：1－5.

［9］Zhuck N P.Scattering of EM waves from a slightly rough surface of a generally anisotropic plane-layered half space［J］：IEEE Trans on Anten and Prop，1997（45）：1774－1782.

［10］Sultan－Salem A K，Tyler G L.Validity of the kirchhoffapproximation for electromagnetic wave，scattering from fractal surface［J］.IEEE Trans on Geosci Remote Sensing，2004，42（9）：1860－1870.

［11］任新成，郭立新，刘生春.基于微扰法的高斯粗糙面电磁散射研究［J］.延安大学学报，2006，25（1）：1－2.

［12］Kim Y，Jaggard D L.Band－limited fractal models of atmospheric refractivity fluctuation［J］.JOpt Soc Am，1988，A5（4）：475－480.

［责任编辑 贺小林］

Electromagnetic Scattering from 1D Band Lim ited Weierstrass Fractal Rough Surface Using the Small Perturbation M ethod

SUN LE，REN Xin-cheng，TIANWEI，NIUWen-jun
（School of Physics and Electronic Information，Yanan University，Yanan 716000，China）

The electromagnetic scattering from the rough surface with the plane wave incident is studied using the small perturbation method，the actual rough surface is simulated with lD band limited weierstrass fractalrough surface，the formula of the scattering coefficient is derived combined with the power spectral density of the 1D band limited fractal rough surface.The angular distribution of the scattering coefficient of HH polarization isobtained by numerical implementation.The influence of fractal dimension，the dimension interzone，the spatial fundamental frequency，the RMS of rough surface fluctuation and the frequency of the incidentwave on the scattering coefficient is discussed.The fractal characteristics，the basic characteristics，the zonal characteristics and the characteristicswith varying of incident wave frequency of the electromagnetic scattering from the lD band limited weierstrass fractal rough surface are obtained.

electromagnetic scattering；1D limited weierstrass fractal rough surface；the small perturbationmethod；the scattering coefficient

TN011

A

1004－602X（2014）04－0019－04

10.3969／J.ISSN.1004－602X.2014.04.019

2014-07-06

2012年地方高校国家级大学生创新创业训练计划项目（1070110014003）

孙 乐（1990—），男，陕西高陵人，延安大学物电学院学生。*通讯作者