翼型不确定性量化中正交匹配追踪的应用

2023-10-17胡汉铎宋彦萍俞建阳刘瑶陈浮高文秀

航空学报 2023年18期

胡汉铎，宋彦萍，俞建阳，刘瑶，陈浮，高文秀

哈尔滨工业大学能源科学与工程学院，哈尔滨 150001

随着航空技术的不断发展，对飞行器的飞行性能要求不断提高［1］。机翼作为飞行器升力的主要提供部件，其性能水平直接决定了飞行器的气动性能和安全裕度［2］。然而，在实际加工、装配和飞行过程中，由于制造误差［3］、结冰［4-5］和腐蚀［6］等因素的存在，机翼的外形不可避免地与设计的理想形状存在偏差，翼型几何在一定的范围内随机变化，即存在几何不确定性。不确定性因素的存在会使机翼性能发生波动，进而导致飞行器性能恶化，甚至带来安全隐患［7］，因此开展不确定性量化、获得机翼性能参数在考虑不确定性因素下的随机响应特性，对于评估飞行器安全性能、指导机翼鲁棒性设计具有重要研究意义［8］。

在不确定性量化方法方面，蒙特卡洛采样（Monte Carlo Sampling，MCS）和混沌多项式展开（Polynomial Chaos Expansion，PCE）已经被国内外学者广泛应用于翼型的不确定性研究中。Loeven等［9］于2007年提出用概率配点法（Probabilistic Collocation Method，PCM）采样求解混沌多项式系数，并将其用于NACA0012翼型的不确定性量化，只考虑来流马赫数的变化，根据概率配点法，只需要5个配点即可量化翼型升力和阻力的概率密度分布；不久后，Loeven等［10］将概率配点法应用于考虑3个几何不确定性因素的NACA5412翼型不确定性量化，配点数增加到27个。高远等［11］使用3阶非嵌入式混沌多项式展开，针对考虑来流马赫数和攻角不确定性的RAE2822翼型开展不确定性量化，使用25个样本可以在效率与精度之间取得平衡。于佳鑫等［12］针对S809翼型，考虑了12个变量的几何不确定性，对比了蒙特卡洛采样和稀疏网格配点法获得收敛量化结果所需的样本数和精度，对于蒙特卡洛采样方法，当采样数达到2 000时才收敛，而3阶Hermite多项式需要313个样本就可以得到与蒙特卡洛采样一致的结果。考虑到蒙特卡洛采样需要大量样本，Liu等［13］利用代理模型技术，首先用100个训练样本构建Kriging代理模型，该模型可以代替耗时的CFD仿真预测RAE5243翼型上不同压敏涂层厚度下的升力系数，误差不超过0.6%，然后使用容易计算的代理模型进行了107次蒙特卡洛采样，获得了几何不确定性对翼型表面流动的影响。相比而言，蒙特卡洛采样直接模拟实际随机过程，获得的统计量精度高，可信度好，但样本量需求十分庞大；混沌多项式展开将翼型性能参数的随机响应在混沌多项式基底上展开，利用多项式系数计算均值和标准差，样本数需求有所降低，而精度与蒙特卡洛采样相近。尽管如此，通过概率配点法求解多项式系数要求样本数量不少于多项式基底数，限制了其在考虑高维不确定性因素的复杂系统中的实际应用。

近年来，压缩感知技术在信号处理领域取得迅速发展［14］，其利用原始信号的稀疏性质，只需要很少的观测样本就可以用特定的重构算法精确重构原始信号［15］。针对不确定性量化中样本数需求较多的问题，研究人员开始探索将压缩感知技术应用于不确定性量化中。Liang等［16］详细探讨了压缩感知理论对研究对象的基本要求，包括系数的稀疏性和观测矩阵的受限等距性质（Restricted Isometry Property，RIP），指出混沌多项式展开在实际不确定性量化研究中满足上述条件，并通过测试函数验证。Yang等［17］利用压缩感知重构混沌多项式系数，并在若干测试函数和偏微分方程组上测试，输入变量维度涵盖20～500范围，所提出的方法即使在小样本集上也能够获得良好的精度。陈江涛等［18］利用稀疏混沌多项式展开方法，在翼型绕流湍流模型稀疏不确定性和烧蚀材料物性参数不确定性2个算例上进行研究，对于输出量的统计特性稀疏混沌多项式展开能够进行准确预测。Lu等［19］将压缩感知中的正交匹配追踪算法（Orthogonal Matching Pursuit，OMP）用于重构混沌多项式系数，分别在考虑几何不确定性的NLR7301翼型流动和考虑壁面热流不确定性的强迫对流换热上对比验证，结果表明，OMP算法的优势在于达到相同的精度要求时收敛更快，观测样本量需求更少，适合复杂问题的不确定性分析。赵欢等［20］采用稀疏混沌多项式重构算法，对高速自然层流翼型LRN1015开展考虑来流马赫数和升力系数不确定性的稳健性优化，得益于自适应前向-后向选择的稀疏重构算法，不确定性分析效率得到改进，获得了更好的稳健性设计结果。尽管在压缩感知技术与混沌多项式展开相结合方面国内外学者已经开展了初步探索，但在翼型几何不确定性量化领域的研究仍相对较少。

本文考虑RAE2822翼型的几何不确定性，将压缩感知技术用于气动性能参数随机响应的不确定性量化，利用正交匹配追踪算法重构混沌多项式系数，并且将获得的统计特性与传统的蒙特卡洛采样和满秩概率配点法进行对比分析，探讨正交匹配追踪重构算法在收敛性能和样本需求等方面的优势，为压缩感知技术应用于翼型不确定性量化领域的进一步研究提供参考。

1 不确定性量化方法

1.1 混沌多项式展开

不确定性量化中的混沌多项式展开（Polynomial Chaos Expansion，PCE）方法将系统不确定性输入和随机响应之间的映射关系在一系列正交多项式基底上展开。尽管现实中大多数信号都不具备稀疏性质，但经过混沌多项式展开后的系数将逐渐衰减，因此可以认为具有一定的稀疏性。

混沌多项式展开可以表示为［21］

式中：y为系统随机响应输出；x为系统不确定性输入；Hi为与不确定性分布相对应的混沌多项式基底。在本文研究范围内，假定几何不确定性因素满足正态分布，对应的多项式基底为Hermite基底，其形式可以按照递推公式［22］推导；ai为第i项基底对应的多项式系数，需要通过采样获得若干组系统输入-输出响应值后，利用最小二乘法求解：

其中：H可以写为矩阵形式，行数为采样样本数N，列数（Npc+1）为总共的多项式项数：

Npc与不确定性输入变量的维数m和多项式基底阶数p有关：

从式（4）可见，随着输入维数的多项式基底阶数的增加，基底总数呈阶乘增长，当不确定性因素较多、系统响应非线性较强时，多项式基底个数剧增，求解系数所需的样本数也随之增多，导致计算成本过高，即面临“维数灾难”的困境。

1.2 压缩感知理论

在求解多项式系数a时，研究人员希望需要的样本量尽可能少，以提高不确定性量化效率。当样本数N小于多项式基底项数时，式（3）中的H矩阵行数小于列数，式（1）的求解转变为欠定方程组问题，压缩感知理论正是关注此类问题的求解。从线性方程组的角度考虑，欠定方程组没有唯一解，但压缩感知理论证明，如果待求解向量满足一定的条件，例如具有稀疏性，那么通过特定的重构算法可以获得唯一解。对于不确定性量化问题而言，如果系统响应在混沌多项式基底上展开的系数足够稀疏，那么系数向量可以通过如下l0范数最小化问题来求解：

式中：H矩阵起到观测矩阵的作用；||a||0表示系数向量a中非零元素的个数，反映了系数向量的稀疏程度；ε为允许的拟合容差。

然而，直接求解上述l0范数最小化问题是一个NP-hard难题。为此，开发了一系列重构算法，以可接受的计算成本获得近似的最稀疏解，包括凸优化算法、贪婪类算法等。其中，正交匹配追踪（Orthogonal Matching Pursuit，OMP）是贪婪类重构算法的代表，其主要优势是计算成本低、收敛速度快，适合交叉验证。

1.3 正交匹配追踪算法

重构算法是压缩感知能否精确重构原始信号的核心，根据应用场景选择合适的重构算法至关重要。本文采用贪婪重构算法中的正交匹配追踪重构混沌多项式系数。

由于遍历H矩阵中所有列向量基底组合过于复杂，正交匹配追踪算法采用贪婪思想，每次从列向量基底中选择与残差最相关的基底，添加到已有的支持集中，在选出的基底上尝试重构多项式系数，系数向量中只有选出的基底对应的系数不为零，而其余系数均为零，以此实现重构系数的稀疏性。上述步骤迭代若干次，直至残差降至指定的容差范围内，算法流程如图1所示。

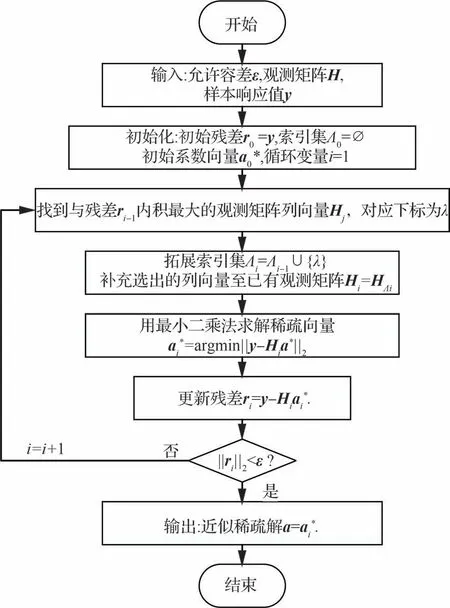
图1 正交匹配追踪算法流程Fig.1 Flowchart of OMP

由于在每一个迭代步，OMP算法都是寻找能使残差下降最快的基向量，因此能够以较快的速度收敛到唯一的稀疏解。

通过重构算法可以获得系数向量a，进而获得混沌多项式展开完整的表达式，可以根据式（1）计算系统输出响应。对于不确定性量化问题，研究人员更加关注随机响应的统计特性，包括均值μ和标准差σ，两者可以直接通过混沌多项式系数分量来估计：

1.4 标准测试算例验证

综合上述方法，建立了一个可以减少样本数需求的不确定性量化框架，如图2所示。首先确定不确定性的输入维度和概率分布，然后根据概率分布和多项式阶数生成混沌多项式基底，所需的样本从高斯积分点中随机选取，确定观测矩阵H。对于翼型流动问题，通过计算流体力学（Computational Fluid Dynamics，CFD）仿真获得各个样本下的气动力系数和其他关注的流场量，最后在建立的样本集上使用正交匹配追踪重构算法，求解混沌多项式系数，并获得所关注流动参数的统计特性。

图2 不确定性量化流程Fig.2 Uncertainty quantification framework

为了验证上述不确定性量化框架的精度，本文首先在Ishigami测试函数上进行算例验证。该函数具有很强的非线性，在不确定性量化研究中广泛用于精度校验［23］。

该函数的定义为

其均值μ和标准差σ可以通过理论分析精确计算，作为评估不确定度量化误差的基值。将上述不确定性量化框架用于该测试算例，并与理论值和传统的不确定性量化方法，包括蒙特卡洛采样和满秩概率配点法（Full Rank Probabilistic Collocation，FRPC）进行对比。

图3给出了均值和标准差相对误差随样本数增加的变化过程。相比之下，3种方法中蒙特卡洛采样收敛最慢，重构误差随着样本数的增加缓慢降低。混沌多项式展开基底输入维数为3，多项式阶数取13，根据式（4）可知共有560个基底，当变量数小于基底数时，方程组欠定，难以获得精确解，故均值和标准差的重构误差都较大；而当样本数等于基底数时，方程组满秩，可以用最小二乘法求得精确解，因而重构误差曲线陡降。而采用同样混沌多项式基底的正交匹配追踪算法，仅需140个样本即可收敛到与满秩概率配点法相同的精度水平，这是因为560个混沌多项式基底对应的系数向量具有稀疏性，即大部分系数幅值接近于0，表明这些系数对应的多项式基底影响作用较小，而正交匹配追踪算法可以优先筛选占主要影响的基底并求解对应的系数，从而实现用较少的样本获得精确的不确定性量化结果。

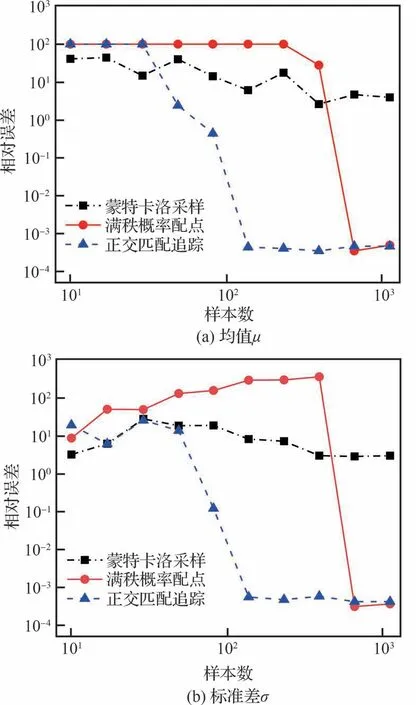
图3 蒙特卡洛采样、满秩概率配点和正交匹配追踪算法对Ishigami测试算例的预测误差Fig.3 Prediction errors of Ishigami function by MCS，FRPC and OMP

2 RAE2822不确定性量化分析

在通过测试算例验证所用方法的精度后，将上述框架用于RAE2822翼型的几何不确定性量化分析。首先对所采用的数值模型进行验证，将仿真结果与试验结果对比。为了描述翼型几何不确定性变化，采用类函数/形函数变换（Class-Shape Transformation，CST）将原始翼型参数化，将翼型几何的不确定性变化转变为CST参数的随机波动，并确定各参数概率分布规律和变化范围。最后，在本文所研究的翼型几何不确定性因素下，用混沌多项式展开和正交匹配追踪算法开展不确定性量化，获得翼型升力系数、阻力系数和其他主要流场量的统计特性，并与蒙特卡洛采样和概率配点法在收敛性、量化精度和样本数需求等方面进行对比，以验证所用方法的有效性。

2.1 数值模型验证

RAE2822翼型绕流是典型的二维跨声速可压缩流动，被欧洲EUROVAL项目和AGARD选为经典验证算例。Cook等［24］在RAE 8 ft×6 ft（1 ft=0.304 8 m）跨声速风洞中进行流场实验测量，共选择10个工况，通过压力探针测量压力分布，而升力、阻力和力矩系数通过对翼型表面压力进行积分获得。此外，还用边界层探针测量了边界层速度剖面。

RAE2822翼型的几何形状以上下表面离散点的形式表示，为了描述翼型几何形状的不确定性变化，需要用参数化方法将离散的翼型几何点转化为控制参数。本文采用Kulfan［25］提出的类形状/形函数变换方法来拟合原始翼型。CST方法使用类函数C（φ）和形函数S（φ）来定义翼型的几何形状：

式中：φ和ζ是基于弦长归一化的翼型坐标；ζT是尾缘厚度，对于RAE2822类型的圆头尖尾翼型，尾缘厚度为0。

C（φ）是用于定义翼型整体类型的类函数，其表达式为

通过调整N1和N2，可以生成不同类型的翼型，如图4所示。

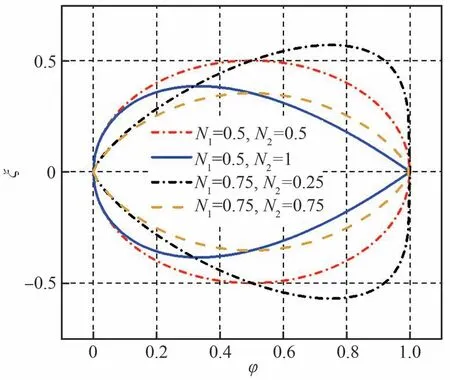
图4 类函数C（φ）决定的不同N1、N2取值对应的基本翼型Fig.4 Basic airfoil determined by class function C（φ）with different N1， N2

对于前缘圆形、尾缘尖形的RAE2822翼型，N1取0.5，N2取1。形函数S（φ）通过多阶Bernstein多项式的叠加来描述翼型的具体形状：

式中：Ai是第i项的权重系数；n是Bernstein多项式阶数（Bernstein Polynomial Order，BPO）。CST参数化方法即是通过控制形函数中的Ai来拟合成不同形状的翼型，拟合误差随着多项式阶数的增加而减小，但与此同时变量Ai的个数也随之增加。

图5给出了不同阶数下的对原始翼型的拟合误差，可见4阶CST已经能够在风洞模型公差范围内拟合RAE2822翼型，可以满足实际应用需要。

图5 不同Bernstein基函数阶数的CST方法对RAE2822翼型的拟合误差Fig.5 Fitting error of RAE2822 airfoil using CST with different BPO

采用4阶CST参数化，上下表面各需要5个参数（A0～A9）来描述无量纲翼型形状；此外，为了保持与实验模型一致以验证数值模型精度，同时考虑弦长不确定性的变化，翼型的弦长c也作为几何参数。因此，总共确定了11个几何参数。

为了验证数值模型，首先进行确定性仿真。在不确定性量化研究中，通常采用来流马赫数Ma为0.734，攻角为2.79°，对应雷诺数Re为6.5×106的工况［26］。在数值仿真验证时，选取与其最为接近的实验测量工况进行仿真，对应的Ma为0.730，攻角为3.19°。为了同时验证经过CST拟合的翼型气动性能，对原始翼型和拟合翼型均进行雷诺平均纳维-斯托克斯方程（Reynold-Averaged Navier-Stokes equations，RANS）模拟，计算域边界距离翼型表面25倍弦长，以避免计算域边界对翼型附近流动的干扰。对计算域划分C型拓扑网格，边界层第1层网格高度由y+值控制，本研究采用SSTk-ω湍流模型，要求壁面上y+＜1。网格节点数通过网格无关性验证确定，进行了一系列网格单元总数逐渐递增的仿真，表1列出了升力系数（Lift coefficient，CL）和阻力系数（Drag coefficient，CD）与实验结果的对比。表中结果表明，当网格单元数达到120 000后，计算结果随网格单元的进一步增加变化不大。因此，在后续仿真将基于129 258单元数的网格开展，以平衡仿真精度和时间成本。该套网格在翼型附近区域的分布情况如图6所示，在翼型上表面中间弦长后的激波存在区域进行网格节点加密，以提高对激波的辨识度。

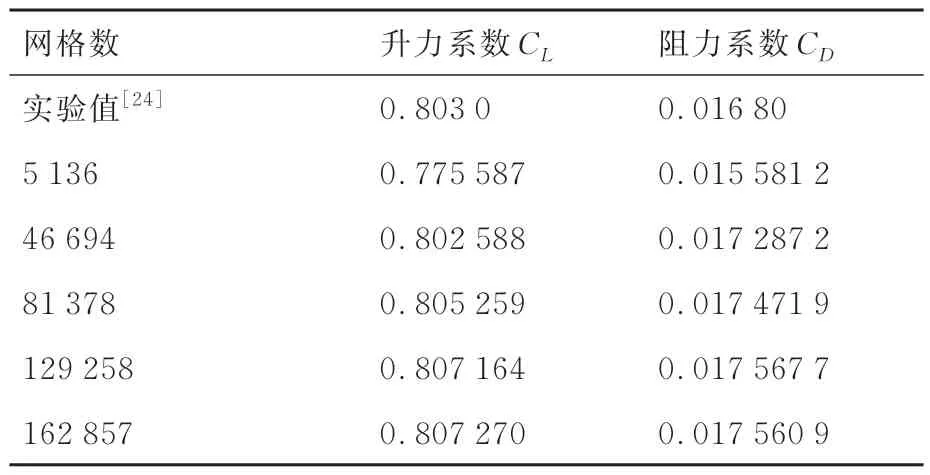
表1 网格无关性验证Table 1 Grid independence test

图6 RAE2822翼型计算网格Fig.6 Computation grid around RAE2822 airfoil

在确定了网格单元数后，用相同的网格拓扑对拟合翼型也划分了计算域网格，图7中给出了原始翼型和拟合翼型表面压力系数（Pressure coefficient，Cp）分布与实验结果的对比，结果表明，经过CST拟合的翼型仿真结果与原始翼型取得一致，从仿真结果层面验证了拟合精度。

图7 原始翼型和拟合翼型压力系数的对比Fig.7 Comparison of original and fitting airfoils on pressure coefficient

2.2 几何不确定性范围和概率分布

在验证数值模型的基础上，可以开展考虑几何不确定性的RAE2822翼型气动性能不确定性量化。由于翼型几何已经通过CST方法进行参数化，因此翼型几何不确定性的变化可以转化为CST参数的随机波动。参考其他有关翼型几何不确定性的研究［27］，针对加工、装配和实际飞行工况等因素导致的实际翼型与原始翼型差异，将翼型弦长的不确定性变化也考虑在内，确定了本研究中RAE2822的几何厚度变化范围为±1 mm。图8中给出翼型前缘和尾缘的不确定性变化边界。

图8 RAE2822在前缘和尾缘的几何不确定性变化范围Fig.8 Geometrical uncertainty range of RAE2822 airfoil at leading edge and trailing edge

11个CST几何参数的范围由图中最薄和最厚的翼型确定，这些参数假设均服从高斯分布N（μ，σ）。为了实现CST参数随机变化时翼型几何能够保持在最薄和最厚翼型之间，采用最小二乘法分别反求加厚翼型和减薄翼型对应的CST参数值，由此确定了11个CST参数能够变化的上下限范围。根据3σ原则，假定此范围为±3σ的边界，由此确定了各变量标准差σ的取值，均值μ则由原始翼型反求CST参数获得。各CST参数的均值μ和标准差σ在表2中列出。

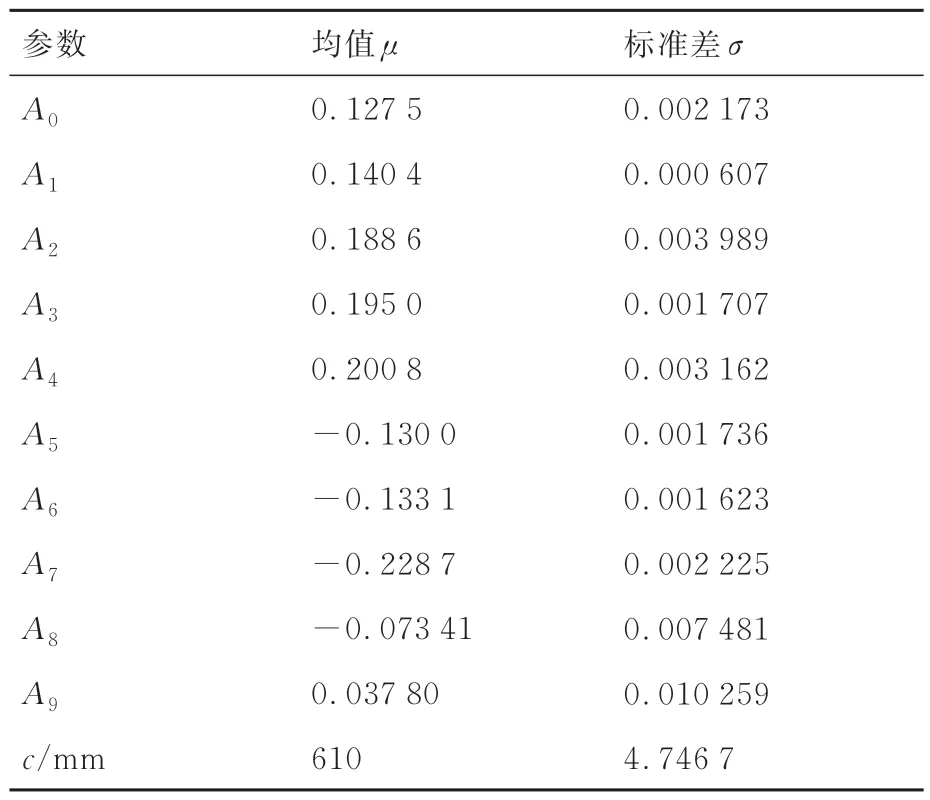
表2 11个CST参数的均值μ和标准差σTable 2 Mean μ and standard deviation σ of 11 CST parameters

图9给出了按照上述CST参数化方法生成的一系列随机翼型，这些翼型分布在加厚翼型和减薄翼型之间，其分布规律表明所采用的方法生成的随机翼型可以覆盖±1 mm的几何不确定性变化区间，可以用于描述翼型几何不确定性变化。

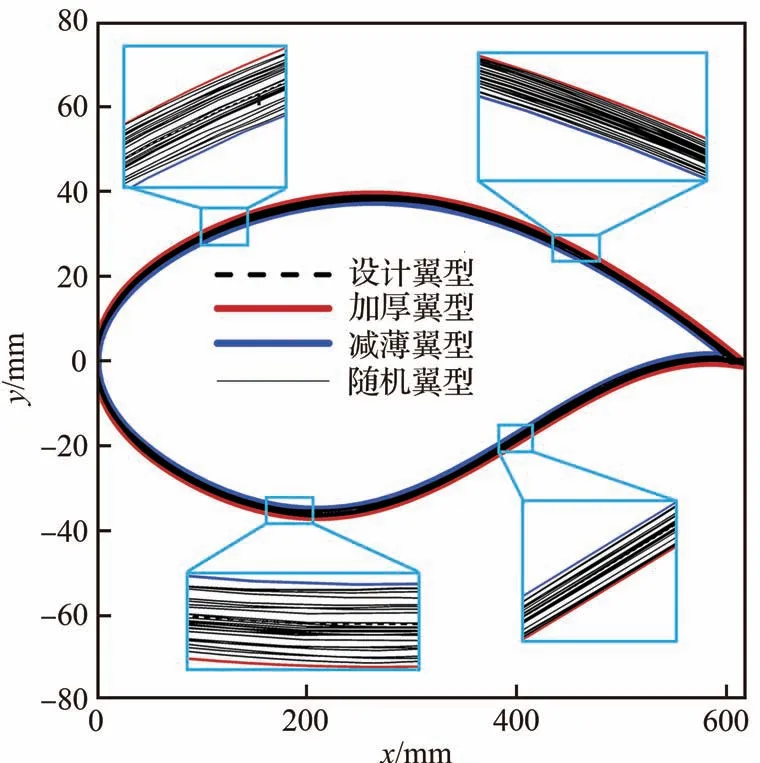
图9 随机翼型几何分布图Fig.9 Distribution of random airfoils geometry

几何不确定性变化范围确定后，采用图2所示的不确定性量化框架，用正交匹配追踪算法求解混沌多项式系数并获得RAE2822翼型气动性能的统计特性，与蒙特卡洛采样（MCS）和满秩概率配点法（FRPC）对比。

2.3 气动力系数对比

表3中列出了3种方法求解的升力系数和阻力系数的统计特性。由于对于实际翼型的不确定性量化问题尚无理论解，考虑到蒙特卡洛采样法模拟真实概率分布采样，样本信息丰富，因此以蒙特卡洛采样获得的结果为参考计算相对误差。

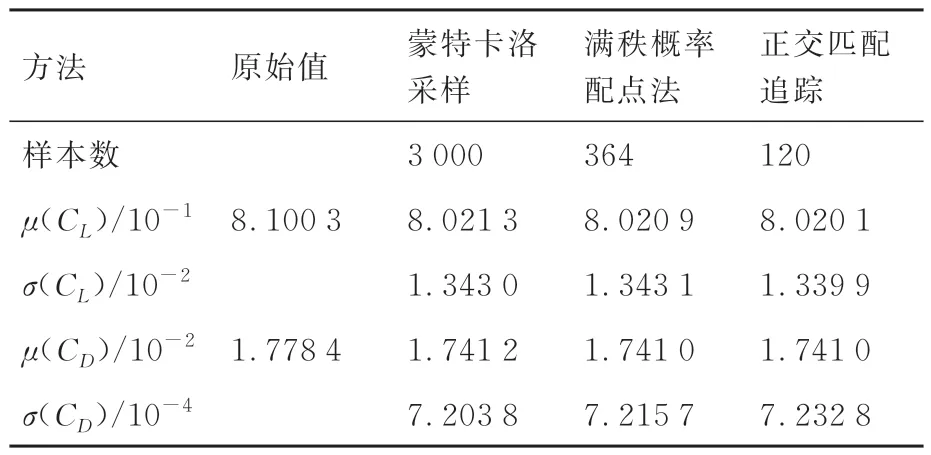
表3 蒙特卡洛采样、满秩概率配点法和正交匹配追踪预测的气动力系数均值μ和标准差σTable 3 Mean μ and standard deviation σ of aerodynamic coefficients predicted by MCS， FRPC and OMP

由表3可知，在几何不确定性作用下，翼型升力系数均值相比于原型下降了约1%，表明几何不确定性的存在导致翼型升力降低；另一方面，几何不确定性导致升力系数和阻力系数出现一定程度的波动，其中阻力系数变化的标准差可以达到均值的4%。比较而言，满秩概率配点法所获得的升力系数和阻力系数与蒙特卡洛采样较为接近，但需要364个样本才能使H矩阵满秩；而正交匹配追踪算法只需要120个样本，即可取得与满秩概率配点法基本一致的结果，表明压缩感知方法可以用相对较少的样本获得较高的精度。

上述结果体现了样本量充足时各方法的预测精度，而图10中则给出不同样本数下的相对误差来比较各方法的收敛性，其中相对误差是以最多样本数下蒙特卡洛采样的结果为基准计算的。3种方法中，蒙特卡洛采样收敛速度最慢，几乎在所有样本数水平下相对误差都是最高的。基于概率配点法的PCE方法直到样本数达到364，即满足满秩条件时才快速收敛，364个样本的结果与1 200个样本量的蒙特卡洛采样方法相比，相对误差减少了一个数量级；而在样本数小于多项式系数个数时，由于方程组欠定，求解误差较大。

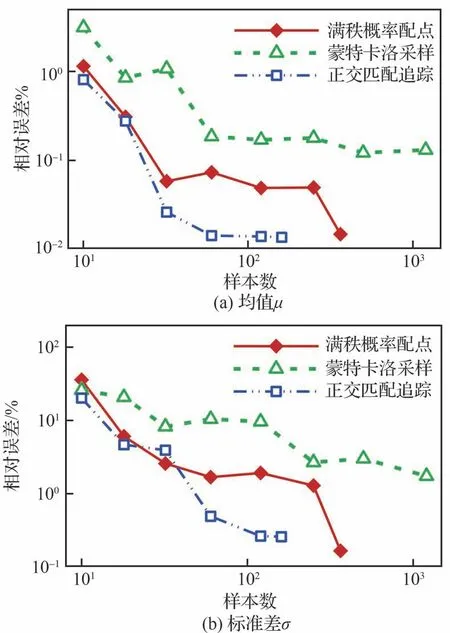
图10 蒙特卡洛采样、满秩概率配点和正交匹配追踪算法收敛情况对比Fig.10 Convergence comparison of MCS， FRPC and OMP

比较而言，正交匹配追踪算法可以用更少的样本获得与概率配点法相接近的精度，特别是当样本数低于满秩要求，相比于概率配点法用最小二乘拟合多项式系数，正交匹配追踪的误差更低或持平。不过，在样本数增加到一定规模之前，正交匹配追踪算法和概率配点法之间的差距并不明显。具体对于本算例而言，均值μ的预测出现显著差异是在样本数达到30以上，而对于标准差σ则是60个样本，表明标准差的准确预测比均值难度更大。

正交匹配追踪算法能够表现出上述优势得益于多项式系数的稀疏性。尽管在实际应用中假设了稀疏性的前提，但重构获得的多项式系数是否足够稀疏仍然需要校验。图11对比了2种PCE方法中多项式基底对应系数的幅值，按基底序号排序。图中的2组系数分别是364个样本的满秩概率配点法PCE和120个样本的正交匹配追踪获得的，为了直观显示多项式系数的相对大小，横纵坐标轴都采用对数刻度。图中系数幅值分布表明，大部分PCE系数都接近于0，如果假定小于10-6的系数可被视为0，那么系数向量确实满足稀疏性条件。从另一角度分析，所有通过正交匹配追踪求解出的系数幅值都大于10-6，这表明该算法能够从所有的多项式基底中筛选出起主导作用的子集，从而利用系数向量的稀疏性精确重构对应的非零系数。

图11 满秩概率配点和正交匹配追踪重构的混沌多项式系数对比Fig.11 Comparison of polynomial chaos coefficients reconstructed by FRPC and OMP

除了对比均值和标准差等统计特性之外，还需要进一步验证概率密度分布。图12中给出了采用蒙特卡洛采样、满秩法PCE和正交匹配追踪预测的升力系数和阻力系数的概率密度分布函数（Probability Density Function，PDF）。图中结果表明，满秩概率配点法PCE和正交匹配追踪能够精确重构出与蒙特卡洛采样结果一致的气动力系数概率分布，且正交匹配追踪只需要120个观测样本，远少于需要364个样本才能满秩的PCE和3 000个样本才能收敛的蒙特卡洛采样。

图12 蒙特卡洛采样、满秩概率配点和正交匹配追踪算法预测的升力系数、阻力系数概率密度函数对比Fig.12 Comparison of probability density function of CL and CD predicted by MCS， FRPC and OMP

综上，在考虑几何不确定性的翼型气动力系数的预测中，压缩感知技术在样本需求量少方面展现出显著优势，能够高效灵活地进行不确定性量化分析。

2.4 流场参数对比

气动力系数是将翼型表面所受压力积分获得的，为了进一步对比流场重构结果，提取翼型上下表面压力系数沿弦长的分布，如图13所示。

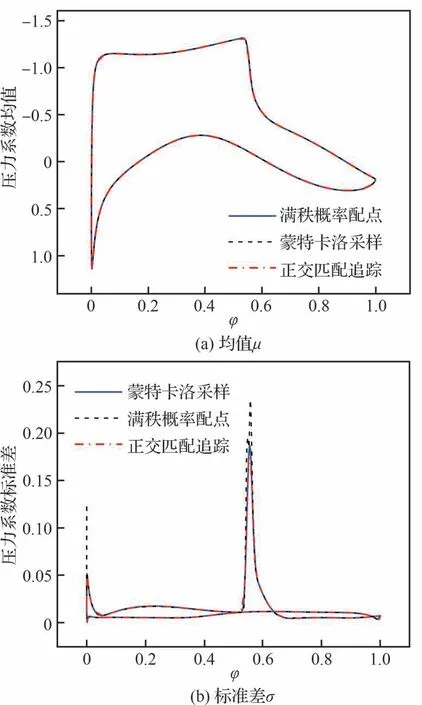
图13 翼型表面压力系数沿弦长的均值和标准差分布Fig.13 Mean and standard deviation of Cp on airfoil surfaces along chord

RAE2822作为典型的超临界翼型，气流在翼型上表面加速降压，从前缘起有一个较为稳定的低压区，直到出现激波后压力骤升，而在下表面上压力系数没有突变，且在翼型尾缘附近压力有所升高，以提供更大升力。在均值方面，满秩概率配点法和正交匹配追踪都可以获得与蒙特卡洛采样相同的压力系数分布规律，结果一致性较好；而在标准差方面，对于压力波动不明显的区域，包括翼型上表面没有激波的区域和整个翼型下表面，标准差σ的预测结果也很接近，3种方法的主要差异体现在60%弦长附近的激波所在区域。几何不确定性的存在使得翼型偏离设计形状，不但会使激波的位置发生改变，激波强度也会因波前气流加速程度不同而变化。由于气流经过激波后压力骤升，激波强度和位置的变化将导致激波所在区域压力系数变化剧烈，即标准差增大，同时不同不确定性量化方法之间标准差预测的差异也被放大。相比而言，在标准差最大的位置，正交匹配追踪的结果更加接近蒙特卡洛采样的参考值，而满秩法PCE的结果则高估了压力系数的波动程度。除了激波所在区域之外，翼型前缘压力波动也较为显著，这是因为翼型下表面驻点位置因几何形状发生微小改变而移动。

几何不确定性的存在不仅影响着翼型表面压力，同时也改变了翼型附近的其他流场参数。在图14中，给出了蒙特卡洛采样、满秩法和正交匹配追踪算法重构的马赫数均值和标准差分布，与前述的气动力系数不同，流场马赫数的重构是在每个网格节点上进行的。正交匹配追踪算法对马赫数均值的预测在大多数位置上与蒙特卡洛采样非常接近，上表面空气从前缘开始加速至超声速，经过激波后变为亚声速，马赫数骤变。标准差的差异主要体现在60%弦长附近的激波区域，这也与压力系数分布呈现的规律一致，几何不确定性影响了激波出现的位置以及激波前后马赫数差值，重构激波区域内马赫数的概率特性也更具挑战。正交匹配追踪的结果表明，翼型附近区域的流场参数变化同样可以通过稀疏重构的方式以一定的精度准确预测，且所需样本量更少，从而在不确定性量化中展现出显著的优势。