Fisher线性判别式阈值优化方法研究

李艳芳　高大启

(华东理工大学信息科学与工程学院　上海 200237)



Fisher线性判别式阈值优化方法研究

李艳芳高大启

(华东理工大学信息科学与工程学院上海 200237)

摘要Fisher线性判别式FLDs(Fisher linear discriminates)的常用阈值对不平衡数据集分类效果较差。以不平衡数据集为应用背景，主要研究各种阈值对FLDs分类性能的影响。认为影响 FLDs性能的主要是类间分布区域不平衡而不是样本数不平衡，因此提出多个经验阈值，并依据分类精度从中选择优化阈值。大量实验结果表明，所提出的阈值优化选择方法能有效提高FLDs对不平衡数据集的分类性能。

关键词分类Fisher线性判别式阈值不平衡数据集

0引言

线性分类器是统计模式识别中最简单的一类[1]。它假设两类样本可以被一个超平面粗略的分开，很多情况下可以得到不太差的结果，由于不容易产生过拟合，有时甚至能获得比复杂分类器更好的效果。并且由于对计算资源要求低，容易实现，在实际中被广泛应用[2]。常见的线性分类器有Fisher线性判别式(FLD)[3]、单层感知器[4]以及线性支持向量机[5]等。

FLD通过最大化准则函数—类间散度和类内散度之比来寻找最能将样本分开的投影方向，通常能取得比较好的效果[6]。但是FLD只能确定决策平面的法向量，却不能确定最终决定分类平面位置的阈值[7]。常用阈值在不平衡数据集中往往过分偏向某类样本，导致分类效果不佳[8]。本文通过研究在不平衡数据集中各种阈值对FLD分类性能的影响，提出影响分类器性能的主要是样本分布区域的不平衡，而不是样本数的不平衡。考虑到样本数和样本分布区域等因素，我们提出多个经验阈值以及根据分类精度或具体的评价指标，选择优化阈值。不同阈值可能适用不同的样本分布，实验证明利用本文提出的阈值优化选择方法，在实际中根据具体情况选择合适的阈值，确实可以提高分类性能。

1FLD基本原理和常用阈值

在两类{ω1,ω2}问题中，用x=(x1,x2,…,xn)T表示n维输入空间中一个样本，则线性分类器的判别函数可以表示为：

g(x)=wTx+w0=wTx-θ

(1)

其中,w=(w1,w2,…,wn)T为权向量，θ=-w0为阈值。从而：

π:g(x)=wTx-θ=0

(2)

就是决策平面，其中w就是决策平面的法向量。于是g(x)>0时可以决策x∈ω1，g(x)<0时x∈ω2。

Fisher线性判别式通过最大化准则函数[6]：

(3)

(4)

这样式(3)便可写成关于w的表达式：

(5)

其中SB代表类间散度矩阵，SW代表总类内散度矩阵，且：

SB=(u1-u2)(u1-u2)T

(6)

SW=S1+S2,Si=∑x∈ωi(x-ui)(x-ui)Ti=1,2

(7)

化简式(5)，最终可得权向量为：

(8)

从式(8)中可以看出权向量只受到类内散布矩阵和两个均值向量的影响。

通过最大化准则函数可以确定最佳投影方向，但是当样本按投影方向投影到一维空间后，还需在一维空间中确定一个点即阈值θ，来将两类样本分开。不同阈值对分类结果影响很大，常用的阈值有θ1和θ2[6]。

(9)

阈值θ1即样本总均值在w方向上的投影。设第p个训练样本xp的期望输出为dp，两个类别{ω1，ω2}中所有训练样本的误差平方和为：

(10)

(11)

令ε是一个充分小的正数，当xp属于第ω1类时，dp→ε，当xp属于第ω2类时，dp→-ε，则：

(12)

实际上dp代表了样本到决策平面的代数距离的期望值，ε→0就意味着所有样本全部落在决策平面上，这与实际情况不符，所以采用阈值θ1的分类器效果可能不会很好。

假设两类样本的类条件概率密度都服从正态分布，由最小贝叶斯误差率原则可知在决策点即阈值θ处满足后验概率相等，即：

(13)

(14)

即投影均值的中点阈值θ2。

2经验阈值及其优化

2.1样本不平衡因素

在研究不平衡数据集时，通常用两类样本数之比，即负类(样本数多的一类)样本数/正类(样本数少的一类)样本数，来表示样本集的样本数不平衡率。然而影响不平衡问题的因素除了样本数外还有样本分布区域的不平衡，而且对于线性分类器，样本分布区域不平衡的影响更大。

假设两类样本集中正类样本数为3，负类样本数为30，不平衡率为30/3=10。如图1所示，负类样本数和样本分布区域都大于正类，采用阈值θ2时，决策平面偏向多数类方向，原本线性可分的样本集却没有被全部正确分类。图2所示两类样本数不变，仍是负类样本数大于正类样本数，但是负类样本分布区域小于正类，此时决策平面的位置偏向了少数类。从样本数来看，样本数不变，决策平面偏向的方向却完全相反；从样本分布区域来看，分布区域大小变化，决策平面偏向的方向也相反。因此我们认为决策平面位置的变化主要受样本分布区域而不是样本数的影响。

图1　样本不平衡时决策平面的位置(A)图2　样本不平衡时决策平面的位置(B)

图3中两类的样本数依然不变，分别为3和30，但是由于其分布区域大小基本相同，此时FLD分类器可以很好地将两类样本分开，两类样本到决策平面的最小距离基本相同。图4中尽管两类样本数平衡，但是样本分布区域却不平衡，此时决策平面仍然会偏向样本分布区域大的一方，对其不利。

图3　样本分布区域平衡时决策平面的位置图4　样本分布区域不平衡时决策平面的位置

2.2经验阈值

在不平衡数据集中常用阈值会使得分类器对某一类样本有利，而对另外一类不利，而这是我们不希望看到的，因此本节将样本不平衡因素考虑进去，提出几个经验阈值。

由式(14)可以看出，θ2与样本数和分布区域无关，只要两类的均值向量不变，阈值就不变。

(15)

受θ1启发，将两类样本数N1、N2的位置调换，可得：

(16)

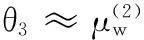
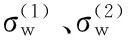
(17)

当ω1类的分布区域大于ω2类时，阈值θ4会向ω2类方向移动，对样本分布区域大的类有利，与样本数没有直接关系。

将θ3与θ4结合起来，θ5考虑到了样本数和样本分布区域两个因素：

(18)

实验证明在样本充足时，随着样本数不平衡度的增加，θ3的变化要大于θ5，从而θ5与θ3一样有利于多数类。

定义类内总体绝对偏差为：

(19)

同样考虑到样本分布区域，但是用类内总体绝对偏差表达样本分布区域的差异，可以得到阈值：

(20)

从计算过程可以看出，它也会受到样本数的影响。

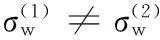
(21)

解此方程可以得到另外一个阈值：

(22)

阈值θ7考虑到实际中两类样本方差不一定相同的情况，可能会取得比较好的效果。从式(22)可以看到，其最终结果只用到了样本投影均值和方差，所以θ7受样本数影响不大。

(23)

(24)

与θ6的计算过程相似，会受到样本数的影响。

定义类内总体平均绝对偏差为：

(25)

用其代替θ6中的总体绝对偏差，可得：

(26)

同样只考虑两个投影均值之间的样本，可对应得到：

(27)

(28)

将以上各阈值取平均，可得到θ11:

(29)

在统计学习理论中，经常用经验风险最小函数来近似期望风险最小函数，原因是在过去风险最小的在将来也很有可能风险最小[9]。在实际应用中每个数据集的样本分布都不相同，我们可以在上述11个阈值中选取能使当前数据集的分类误差最小(整体识别率Acc最大)的阈值作为当前阈值，所以第12个阈值可以表示为：

(30)

对于不平衡问题，总体分类误差往往不能很好地衡量分类器的性能。对于样本数极度不平衡数据集，把所有样本都归为样本数多的一类，仍然可以得到很好的Acc值，但这时少数类的识别率却为零。我们常采用两类的平均识别率：

Avc=(tprate+tnrate)/2

(31)

或几何识别率：

(32)

来衡量分类器的性能。其中tprate=被正确分类正类样本数/正类样本总数，tnrate=被正确分类的负类样本数/负类样本总数。当我们以Avc或G-mean作为分类器的评价指标时，则同样的方法，这时可以定义θ12为上述11个阈值中能使当前的Avc或G-mean值达到最大的阈值。

3实验结果分析

本文用到的数据集全部来自KEEL-dataset数据库[10]。这些数据集都是两类分类问题，且具有不同的不平衡率。

3.1阈值比较实验

本实验对使用了前11个阈值的FLDs进行比较，共用到了95个不平衡数据集，不平衡率最小为1.8，最大为129，由于篇幅关系不再具体列出。

记阈值为θq，q=1,2,…,12的FLD为FLD_θq。分别用分类器FLD_θq，q=1,2,…,11这11个分类器对95个数据集进行分类，并记录分类结果，包括它们的Acc、Avc和G-mean。

对于每个数据集， 11个FLDs将得到11个不同的Acc结果，根据Acc值的高低对11个FLDs进行排序，可以它们的Acc排名。对每个FLD，求其在95个数据集上的Acc排名的均值，即可得到FLDs的Acc平均排名。

同样的方法可以得到FLDs的Avc和G-mean平均排名。

表1中分别列出了FLD_θq，q=1,2,…,11的Acc、Avc、G-mean值的平均排名。

表1　11个阈值的FLDs对KEEL数据集的Acc、Avc、G-mean平均排名

从表1中可以看出，θ4、θ7、θ9、θ10这四个阈值可以得到Avc，G-mean比较高的FLDs，这说明阈值θ4、θ7、θ9、θ10对解决不平衡问题比较有效。θ3、θ5、θ6、θ8这四个阈值可以得到Acc比较高的FLDs，但是由于Acc指标本身对不平衡数据集的评价缺陷，经常不作为评价不平衡问题的指标。结合2.2节的分析，前四个阈值都考虑到了样本分布区域，且受样本数的影响不大，后四个阈值都受到样本数的影响，从而验证了FLD更容易受到样本分布区域不平衡的影响，而不是样本数的影响。FLD_θ2和FLD_θ11基本上处于排名的中间位置，FLD_θ1基本处于最后一位或倒数第二位。

3.2优化阈值选择实验

在实际应用中，需要根据样本具体分布情况不同，选取适合当前数据集的阈值。本实验验证了利用θ12选择优化阈值可以提高分类性能。

本实验用Avc作为分类器的评价指标，θ12定义为前11个阈值中使当前Avc值达到最大的阈值。分别用分类器FLD_θq，q=1,2,…,12这12个分类器对数据集进行分类，并记录结果。

表2列出了所用到的数据集的统计信息。

表2　部分KEEL数据集的统计信息

续表2

表3列出了FLD_θq，q=1,2,…,12这12个分类器对这些数据集分类的Avc，其中最大值已经用加粗标识出来。

表3　FLD_θq,q=1,2,…,12对部分KEEL数据集分类的Avc值(%)

可以看出，得到最高Avc值的阈值尽管不完全相同，但都是θ4、θ7、θ9、θ10中的某个。除少数数据集如ecoli_0_1_4_6_vs_5和yeast6除外，再次验证了之前的结论。通过θ12选择合适的阈值，确实可以提高分类器的分类性能，例如对数据集page_blocks0，平均精度Avc从θ1的82.88%提高到θ10的86.70%。

4结语

线性分类器虽然属于最简单的一种分类器，但在实际应用中往往能取得比较好的结果。在FLD中，阈值最终决定了决策平面的位置，在不平衡问题中，常用阈值往往会出现偏差，致使分类性能变差。本文研究了不平衡问题对FLDs阈值的影响，提出主要影响FLD性能的不平衡因素是样本分布区域的不平衡，而不是样本数的不平衡，并且提出一些经验阈值以及根据分类精度选择优化阈值。实验证明，考虑到样本分布的阈值对解决不平衡问题更有利，以及在具体问题中利用所提出的优化阈值选择方法选取合适的阈值确实能在提升分类效果，在实际应用中有指导作用。本文主要关注的是两类问题下的阈值选取问题，而在多类情况下阈值的选取问题可能会更加复杂，我们今后将把问题关注于多类问题的情况。

参考文献

[1]JainAK,DuinRPW,MaoJC.StatisticalPatternrecognition:areview[J].IEEETransactionsonPatternAnalysisandMachineIntelligence,2000,22(1):4-37.

[2]BekiosCalfaJ,BuenaposadaJM,BaumelaL.Revisitinglineardiscriminatetechniquesingenderrecognition[J].IEEETransactionsonPatternAnalysisandMachineIntelligence,2011,33(4):858-864.

[3]RozzaA,LombardiG,CasiraghiE,etal.NovelFisherdiscriminatesclassifiers[J].Patternrecognition,2012,45(10):3725-3737.

[4]LecunY,BottouL,BengioY,etal.Gradient-basedlearningappliedtodocumentrecognition[J].ProceedingsoftheIEEE,1998,86(11):2278-2324.

[5]MüllerKR,MikaS,RätschG,etal.Anintroductiontokernel-basedlearningalgorithms[J].IEEETransactionsonNeuralNetworks,2001,12(2):181-201.

[6]DudaRO,HartPE,StorkDG.PatternClassification[M].2nded.NewYork:JohnWiley&Sons,Inc,2000.

[7]GaoDaqi,DingJun,ZhuChangming.IntegratedFisherlineardiscriminates:Anempiricalstudy[J].PatternRecognition,2014,47(2):789-805.

[8]HeHaibo,EdwardoAG.Learningfromimbalanceddata[J].IEEETransactionsonKnowledgeandDataEngineering,2009,21(9):1558-1571.

[9]PernkopfF,WohlmayrM.TschiatschekS.MaximummarginBayesiannetworkclassifiers[J].IEEETransactionsonPatternAnalysisandMachineIntelligence,2012,34(3):521-532.

[10]AlcaláFdezJ,FernandezA,LuengoJ,etal.KEELData-MiningSoftwareTool:DataSetRepository,IntegrationofAlgorithmsandExperimentalAnalysisFramework[J].JournalofMultiple-ValuedLogicandSoftComputing,2011,17(2):255-287.

ON OPTIMISING THRESHOLDS OF FISHER LINEAR DISCRIMINANT

Li YanfangGao Daqi

(School of Information Science and Engineering,East China University of Science and Technology,Shanghai 200237,China)

AbstractThe commonly used thresholds of Fisher linear discriminant (FLD) always have poor classification result on imbalanced datasets. On application background of the imbalanced datasets, in this paper we mainly study the influence of various thresholds on FLD’s classification performance. We argue that for FLDs, it’s the imbalance of inter-class distribution regions rather than sample sizes that mainly impacts the performance of FLDs, and thus we develop several empirical thresholds and select the optimised thresholds based on classification accuracy. Extensive experimental results show that the classification performance of FLDs on imbalanced datasets is improved effectively with the use of the proposed optimised threshold selection method.

KeywordsClassificationFisher linear discriminantThresholdsImbalanced dataset

收稿日期：2014-12-14。国家自然科学基金项目(21176077)。李艳芳，硕士生，主研领域：模式识别。高大启，教授。

中图分类号TP391

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.06.035