基于缩尺试验的船舶大分段吊装动力学研究与验证

2023-10-10桂洪斌杨佳朋

振动与冲击 2023年18期

桂洪斌, 杨佳朋, 张岩, 郭彬

(哈尔滨工业大学(威海) 海洋工程学院,山东威海 264209)

随着造船技术的进步、“绿色船舶”理念的兴起以及海洋经济产业的增长,船舶不断向大型化方向发展。在船舶分段吊装过程中由于分段本身质量很大,起重机小车加速度产生的惯性力与离心力会使吊重产生大幅度摆动,进而影响分段吊装过程中的精确性与安全性。由此,对大型起重设备吊装过程的动态响应分析尤为重要。

对于吊装系统动态响应的研究主要包括钢丝绳动力学建模以及吊装系统动力学建模等内容。目前国内外学者已经对钢丝绳动力学建模做了大量研究。钢丝绳属于一维连续、可变性系统,因自身抗弯模量较低,在起重过程中吊重摆角会受到小车加速度与外部载荷的影响。早期的绳索力学模型主要采用集中质量模型或刚体单元方法[1-2]。ADAMS软件问世后,对于绳索的建模主要以bushing衬套力为主。李海军[3]采用衬套力方法得到矿井提升钢丝绳模型,其变形、振动物理性能、动力学性能与真实绳索性能相吻合。马幸福[4]通过ADAMS软件宏命令实现电梯钢丝绳离散化的建模、轴套力的添加及碰撞接触力的设置,研究的电梯系统的振动特性与钢丝绳的振动特性均符合实际运行规律。

国内外学者大都采用拉格朗日方程来确定吊装过程的动力学模型。Abdel-Rahman[5]等利用拉格朗日方程建立了吊重偏摆系统有阻尼的动力学模型,并采用多尺度法求解了吊重的近似响应。马博军等[6]考虑了小车运动、绳长、环境阻力对负载摆动的影响,根据拉格朗日方程建立三维桥式吊车系统的动力学模型研究桥式吊车这类欠驱动系统的动态特性。Raja Ismail等[7]利用拉格朗日方程建立了包含有效载荷的双摆龙门起重机的动力学模型,并在时域和频域范围内对方程进行了验证,讨论了外部有效载荷对系统动态响应的影响。蔺本浩[8]用拉格朗日法建立吊重动力学模型,分别利用ADAMS软件和MATLAB软件分析绳长、起吊速度、激励频率对吊重动力响应的影响,得到了吊重空间运动轨迹图。Ospina-Henao等[9]利用欧拉经典力学理论与拉格朗日方程得到了龙门起重机运动方程,并利用SimMechanics-MATLAB验证了动态方程的正确性。

以上都是基于数值仿真进行的研究分析,关于试验方面的研究内容较少。尤其是对于大型起重设备,考虑到尺寸以及实际操作的影响,很难对实尺度模型(原型)进行试验研究,因此开展缩尺试验的研究非常必要。目前缩尺试验及相似理论在机构设计中较为成熟,罗英平等[10]对于机构设计中的相似准则、相似常数、相似转换关系提出了较为完整的理论公式;Yin等[11]为研究岸边集装箱起重机的动力性能和抗震性能,根据相似理论提出了起重机的1/50比例模型来进行冲击与振动试验,得到的缩尺试验结果与数值模拟具有良好的一致性。陈喆等[12]通过相似理论和有限元方法确定几何参数和物理参数的相似比,进而研究实际结构的动态响应。滕媛媛等[13]利用缩尺模型试验验证了岸边起重机抗震摩擦耗能器的可靠性。

综上所述,本文采用衬套力方法建立钢丝绳动力学模型,利用拉格朗日法确定船舶大分段吊装系统的动力学模型,根据相似原理设计缩尺模型试验平台,采用数值仿真与模型试验对比的方式对大型起重吊装的动力学模型进行验证与分析,进而归纳不同因素对吊装系统动态响应的影响。

1 船舶大分段吊装系统建模

本文针对船舶大分段吊装系统进行分析,以某4300PCTC汽车运输船分段吊装为例,取其大分段尺寸[14]如表1所示,门式起重机参数如表2所示。

表1 PCTC大分段参数Tab.1 Large segment parameter of PCTC

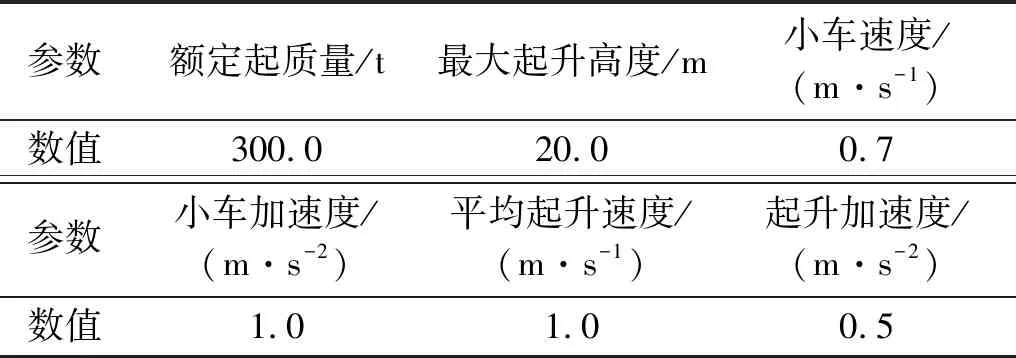
表2 门式起重机参数Tab.2 Parameters of gantry crane

1.1 吊装系统动力学数学模型

为研究吊重系统的横向摆振,本文设定吊重通过弹性绳与小车进行连接,并进行如下假设:①忽略臂架变幅铰点的平移,滑轮处的摩擦,风载、空气阻力;②起重机梁为完全刚性;③在吊装过程中钢丝绳始终受拉。受力示意图如图1所示。

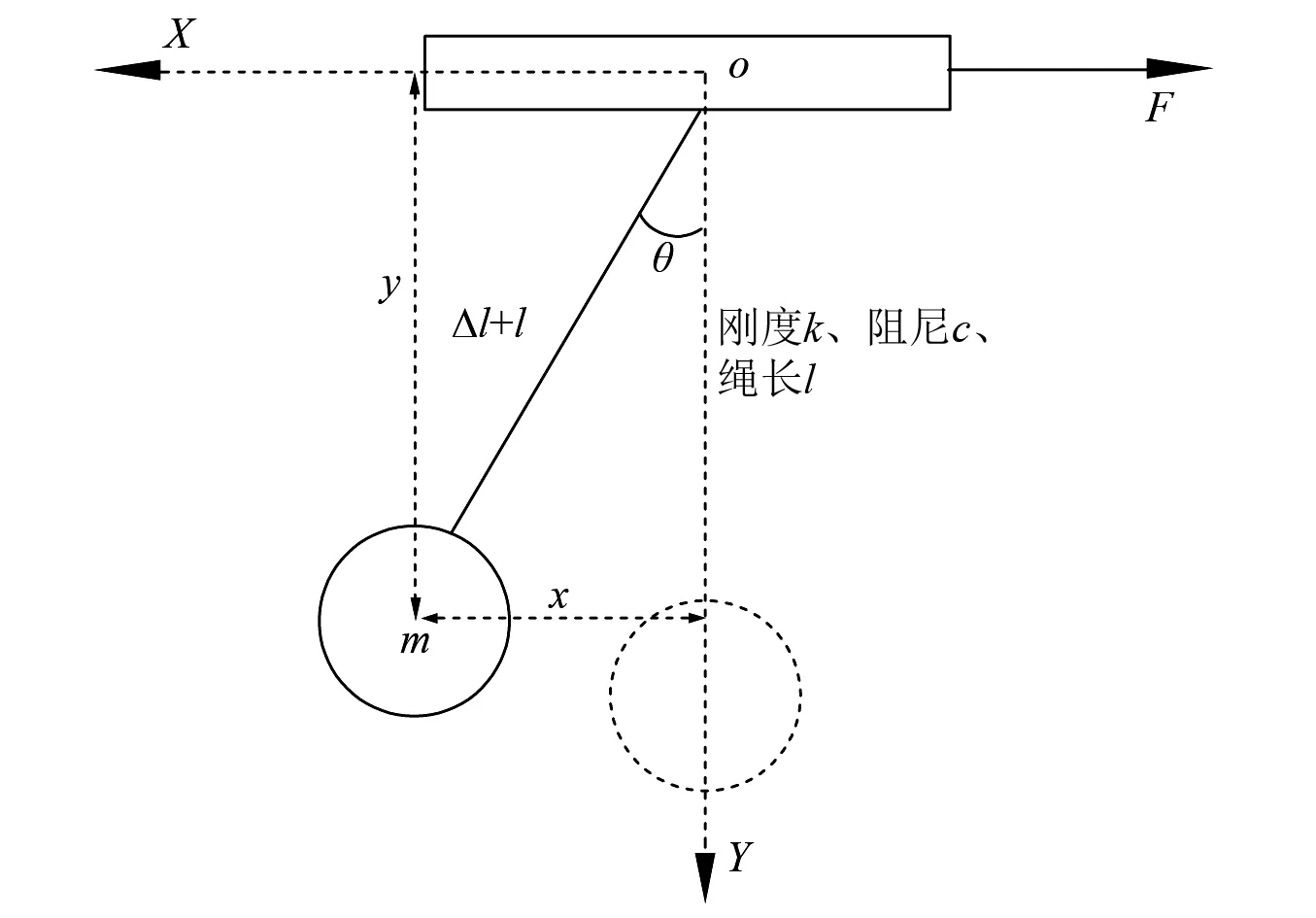
图1 吊装系统受力图Fig.1 Force analysis diagram of hoisting system

图1中:x为吊重沿水平方向(X)位移;y为吊重沿垂直方向(Y)位移;θ为吊重摆角;l为原绳长;m为重物质量;k,c为弹性绳绳刚度、阻尼; Δl为绳伸长量;F为驱动力。各物理量间关系如式(1)所示。

(1)

式中,g为重力加速度。

吊重速度如式(2)所示。

(2)

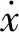
建立拉格朗日动力学方程如式(3)所示。

(3)

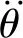
吊重系统摆动过程摆角值比较小,忽略高阶项量,令sinθ≈θ,cosθ≈1,简化得动力学方程如式(4)所示。

(4)

1.2 钢丝绳参数

钢丝绳在ADAMS软件中采用衬套力进行建模,将钢丝绳离散成小刚体圆柱,每段之间通过bushing进行连接,来模拟钢丝绳工作特性,如图2所示。

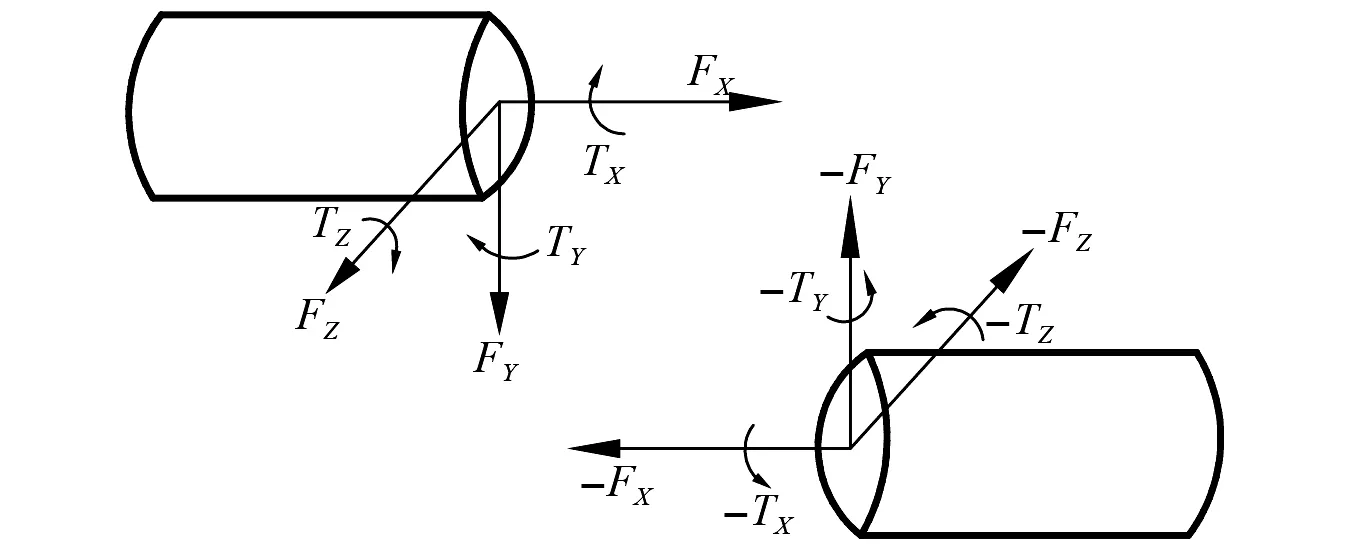
图2 衬套力示意图Fig.2 Diagram of bushing force

衬套力会在连接处的marker点生成{FX,FY,FZ,TX,TY,TZ}的力与力矩,其计算公式如式(5)所示。

(5)

式中:x,y,z为相对位移,m;θx,θy,θz为相对角度,rad;vx,vy,vz为相对速度,m/s;wx,wy,wz为相对角速度,rad/s;k11为拉伸刚度系数,N/m;k22,k33为剪切刚度系数,N/m;k44为扭转刚度系数,N/m;k55,k66为弯曲刚度系数, N/(m·deg);c11为拉伸阻尼系数, N·s/m;c22,c33为剪切阻尼系数, N·s/m;c44为扭转阻尼系数, N·s/(m·deg);c55,c66为弯曲刚度系数, N·s/(m·deg)。

根据钢丝绳材料与参数确定其刚度系数和阻尼系数,保证建立的钢丝绳模型在变形程度和力学性能上与实际钢丝绳相符。钢丝绳材料为45号普通碳合金钢,弹性模量为206 GPa,剪切模量为79.23 GPa,型号为6X19W+FC。在船舶大分段吊装中起重机处于M7工作级别及以上,根据起重机钢丝绳选用规则确定钢丝绳直径[15],如式(6)所示。

(6)

式中:d为选取钢丝绳直径,m;C为选择系数,取为0.112;Smax为绳最大受力,N。进一步计算得出钢丝绳直径为0.054 m。

计算钢丝绳的刚度系数,如式(7)所示。

(7)

式中:E为钢丝绳弹性模量,GPa;A为钢丝绳的截面积,m2;G为剪切模量,GPa;L为起重绳长,m,文中绳长20 m;I为转动惯量,kg/s2。

选取绳阻尼系数为刚度系数的0.1%[16], 根据钢丝绳材料刚度属性确定其拉伸阻尼系数为c11=1.4×104N·s/m, 剪切阻尼系数c22=c33=5.6×103Ns/m,扭转阻尼系数为c44=3.34 N·s/[m·(°)],弯曲阻尼系数为c55=c66=4.3 N·s/[m·(°)]。

1.3 吊装系统动力学仿真模型

在ADAMS软件中利用宏命令进行钢丝绳建模,设定钢丝绳长度为20 m,离散为200个小圆柱刚体,每段之间通过bushing连接,参数设定如1.2节所述。根据起重机参数(见表2)确定模型参数,并在ADAMS软件中进行吊重与小车的建模,设置小车为移动副,小车、钢丝绳、吊重之间采用旋转副连接。吊重系统结构图,如图3所示。

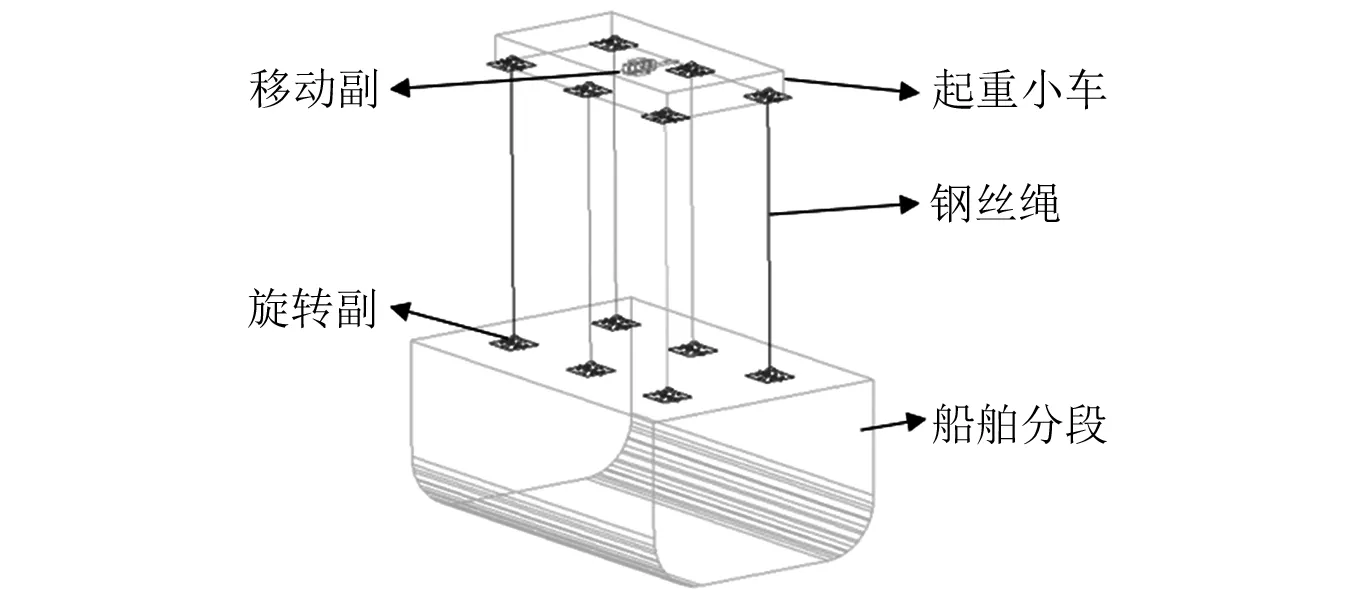
图3 吊重系统结构图Fig.3 Structure diagram of hoisting system

为保证钢丝绳建模符合工程要求,文中首先对ADAMS软件得到的钢丝绳模型进行力学性能验证[17],如式(8)所示,利用宏命令对20 m钢丝绳进行建模,在钢丝绳两端施加拉力10 000 N,进行钢丝绳垂度仿真。得到挠度仿真结果如图4所示。

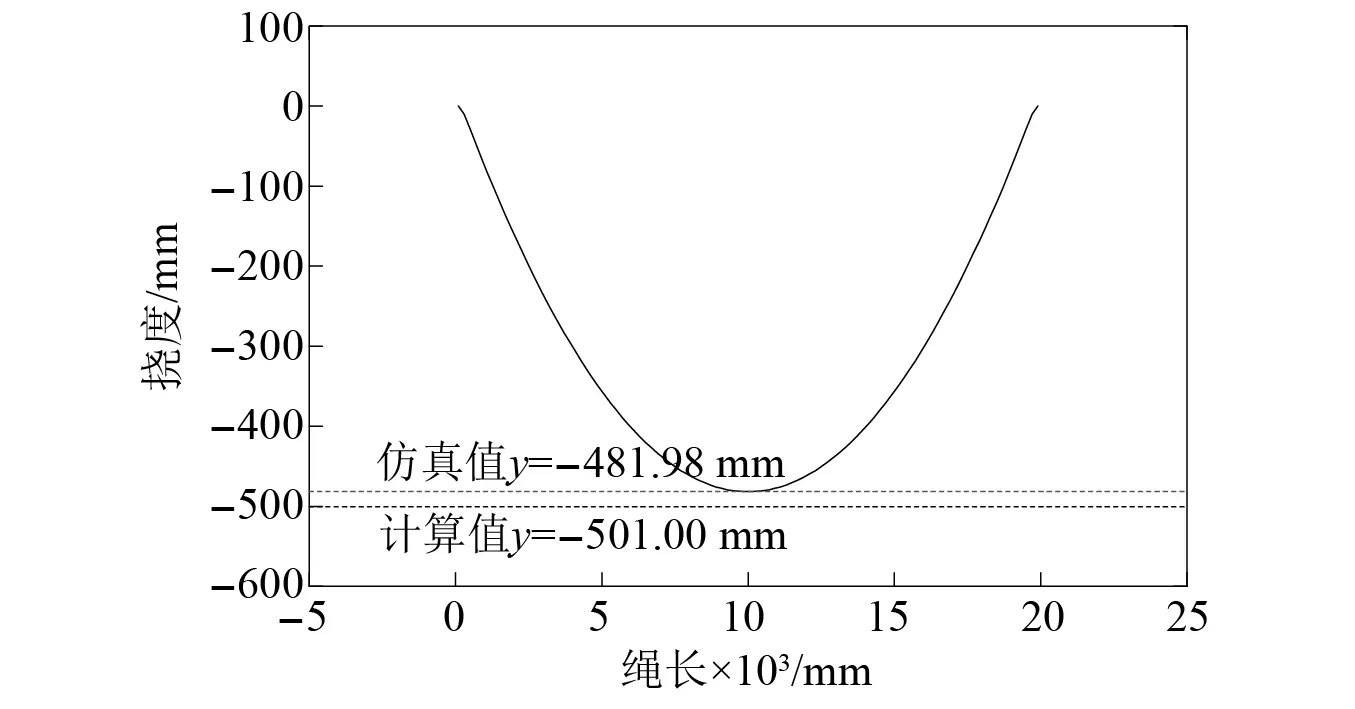
图4 钢丝绳挠度仿真Fig.4 Deflection simulation of wire rope

(8)

式中:q为单位长度钢丝绳质量,kg/m; 型号为6X19W+FC的钢丝绳每千米质量为3.51倍直径的平方值;l为钢丝绳绳长,m;S为钢丝绳拉力,N;β为支座夹角,rad。

垂度计算值为0.501 m,仿真值约为0.482 m,误差为3.9%<5.0%,说明该建模方法满足工程应用的需要。

2 船舶大分段吊装系统建模

2.1 缩尺试验参数选取

根据相似第三定律并结合试验目的,缩尺试验参数选取时应考虑以下条件[18]。

(1) 空间几何条件相似。即要求原型与缩尺模型的几何尺寸、周期、运行速度、空间结构响应等保持相似。

相似常数式(9)定义如下

(9)

式中:cL,ct,cv,ca,cθ,cw分别为几何常数、周期常数、运行速度常数、加速度常数、摆角常数以及角速度常数;lm,tm,vm分别为原型尺寸、周期、速度参数;lp,tp,vp为缩尺模型尺寸、周期、速度参数。

原模型吊装过程中绳摆角与吊重加速度响应应与缩尺模型响应结果一致。

(2) 物理条件相似。即要求原型与缩尺模型的力学特性如钢丝绳刚度系数、阻尼系数以及受载后变形相似。由于原型与缩尺试验模型均采用捻制点接触钢丝绳,其弹性模量E、剪切模量G、阻尼比相差不大,因此钢丝绳力学性能与钢丝绳直径参数相关,相似公式式(10)定义如下

(10)

式中,cl,ck,cG,ckl,cr分别为绳长尺寸、刚度系数、重力、受载后绳形变、绳直径的相似常数。

(3) 边界条件相似。边界条件是指结构表面所受的外力、载荷作用顺序、初始化条件和约束条件等,其中模型约束条件必须与原型相同,不能因此影响结构的工作状态,且必须在模型试验中模拟实际的载荷作用顺序。缩尺试验中采用丝杠滑轨模拟小车运行过程中的移动副;对安装螺栓进行线切割处理形成钢丝绳卡槽,进而与钢丝绳配合形成旋转副。为减小摩擦,旋转副处利用锂基润滑脂进行润滑处理。试验采用与原模型相同的载荷顺序,以此保证边界条件相似。

根据相似理论确定缩尺试验相关参数,如表3所示。

表3 吊装缩尺试验参数Tab.3 Parameters of hoisting system model test

2.2 缩尺试验平台搭建

本文采用步进电机带动丝杠滑块的形式模拟吊装过程中小车的平移运动。

丝杠步进电机负载计算如式(11)所示,选取步进电机的参数如表4所示。搭建的缩尺试验平台示意图如图5所示。

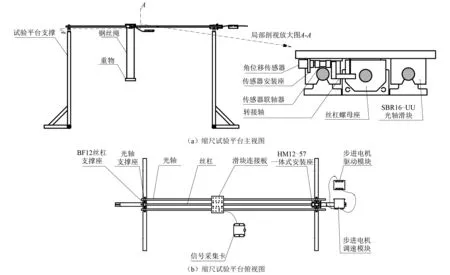
图5 吊装缩尺模型结构示意图Fig.5 Structure diagram of hoisting system model test

表4 步进电机参数Tab.4 Parameters of the stepmotor

(11)

式中:T为电机额定转矩,N·m;s为丝杠导程,m;η为电机工作效率。

采用正交试验形式设计多组试验,观察绳长、绳刚度、重物质量等因素对于吊重动态响应的影响,同时对吊装动力学模型进行验证。试验参数设计如表5所示。

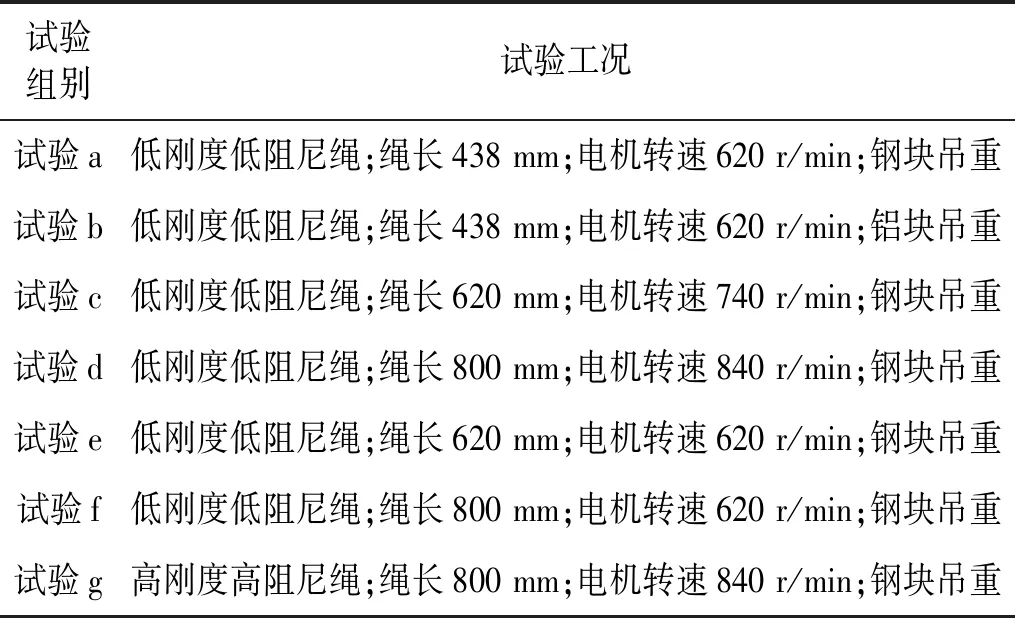
表5 吊装缩尺模型正交试验Tab.5 Orthogonal test of hoisting system model

3 结果分析

3.1 吊装系统动力学仿真模型验证

为验证仿真模型的准确性,文中首先对表5中试验a、试验c、试验d 3种工况进行试验测试,每种工况下进行5次测试。试验动态响应曲线的平均值与相同工况下缩尺模型仿真结果的对比如图6所示,3种工况下的摆角与周期数据如表6所示。

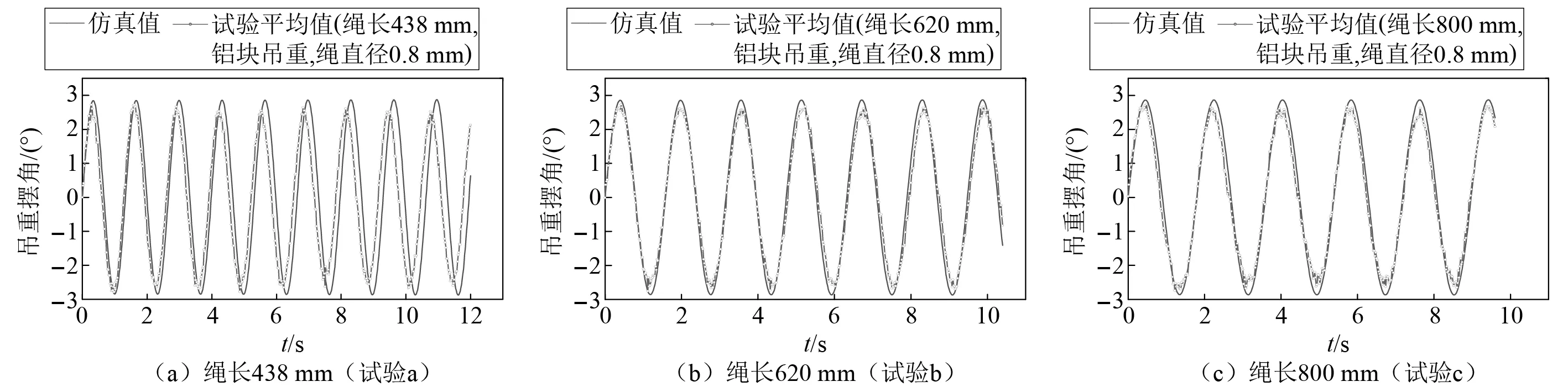
图6 不同绳长下吊装模型试验结果与数值仿真结果的摆角对比Fig.6 Comparison of swing angles between model test and numerical simulation under different rope lengths

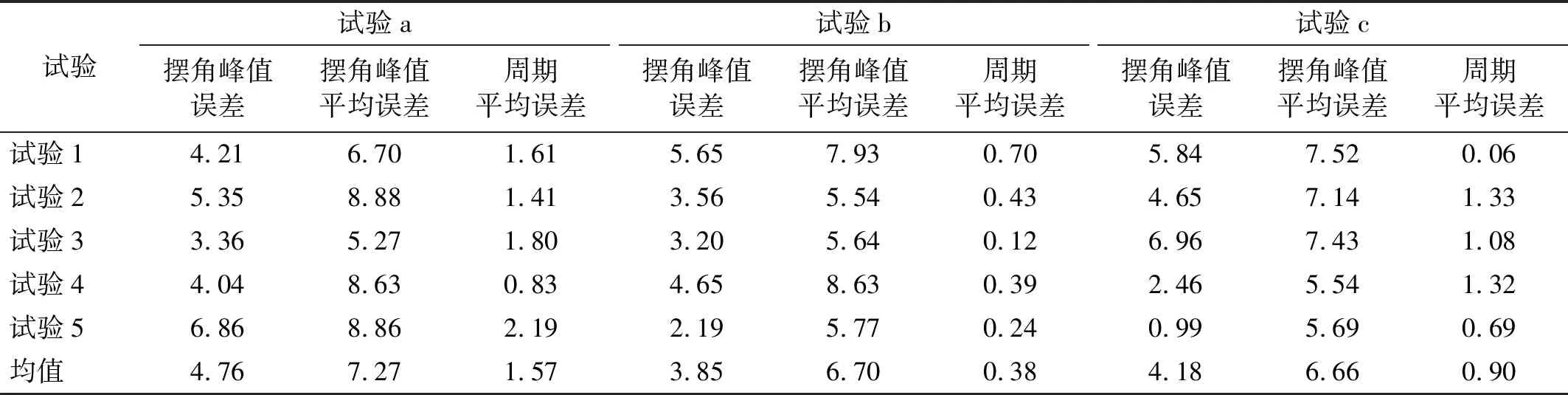
表6 不同绳长下模型试验与数值仿真结果误差对比

由图6可知,仿真结果与试验结果趋势接近,且由表6可知,两者之间的摆角最高峰值误差、摆角平均峰值误差、周期平均值误差均在10%以内,产生误差原因如下:

(1) 搭建的缩尺试验平台,由于丝杆与光轴跨度较大,滑块平移过程中会产生上、下轻微的振动。

(2) 各部件之间摩擦力的大小与仿真中的设置有误差,且忽略了吊重移动过程中的风阻,使试验摆角数值小于仿真值。

(3) 钢丝绳与重物连接时绳长存在误差,质心位置会存在轻微偏移,使吊重有旋转晃动,从而使试验中的摆角偏小;且绳长越短偏心所带来的影响越大,进而在图7(a)绳长较短的工况验证中误差偏大。

图7 缩尺模型动态响应曲线Fig.7 Dynamic response curve of scale model

在表6中,摆角最高峰值误差、摆角平均峰值误差、周期平均值误差最大为4.76%,7.27%以及1.57%,满足工程需要,进而证明了本文ADAMS动力学模型的准确性,为后续通过缩尺试验分析大跨度、大载质量的吊装过程提供了保障与研究基础。

3.2 缩尺试验设计合理性验证

为验证缩尺试验设计的合理性,根据表5中试验a、试验e、试验f 3种工况,本文采用数值分析的方式构建4种模型,分别为绳长20 m的原模型、绳长为0.8 m的缩尺模型1、绳长为0.62 m的缩尺模型2以及绳长为0.438 m的缩尺模型3,进而对比4种模型的动态响应曲线,结果如图7所示。

首先依据式(9)相似常数的设定,摆角常数与加速度常数为1,因此图7(a)、图7(c)中4种模型对应的摆角幅值与吊重加速度幅值近似相等。其次,摆角加速度与吊重速度分别与几何常数呈现反比与正比的关系,因此图7(b)中呈现伴随绳长增加,摆角角速度幅值逐渐减低的现象;而图7(d)中则呈现伴随绳长增加,吊重速度幅值逐渐增加的现象。最后,由于周期常数与几何常数呈现正比关系,因此图7(a)～图7(d)中呈现伴随绳长增加,摆角、摆角角速度、吊重加速度以及吊重速度的周期逐渐增加的现象,即4种模型不同参数动态响应的峰值伴随绳长的增加呈现逐渐靠右的现象。

为进一步定量观察4种模型动态响应参数的变化,本文汇总吊重摆角、加速度、摆角周期、钢丝绳变形量的动态响应结果,如表7所示。由表7可知,摆角与吊重加速度峰值在不同绳长的模型中近乎一致,相对变化不超过2%,与式(9)相似常数设定中保持一致。其次,不同缩尺模型下吊重周期平均值与速度平均值的仿真结果与原模型仿真结果满足式(9)相似常数设定关系;以原模型和缩尺模型2为例,原模型的吊重周期平均值与速度平均值分别为8.98 s和700 mm/s,按照相似关系式(9)计算缩尺模型2的结果为1.581 s和123.25 mm/s;通过数值仿真获得的结果为1.581 s和123 mm/s,两者极为接近。同理得出不同缩尺模型下的角速度仿真结果与原模型仿真结果满足式(9)相似常数设定关系。

表7 原模型与缩尺模型响应参数对比Tab.7 Comparison of dynamic response parameters between prototype and scale model

由图7与表7对比可知,不同缩尺模型下动态响应参数的仿真结果均满足式(9)中相似常数的设定关系。该结果在验证缩尺试验设计合理性的同时,进一步校验了本文数值仿真方法的准确性。

3.3 吊装动态响应的影响分析

3.3.1 吊重质量对吊装系统动态响应的影响

在表5的试验设计中,试验a与试验b的对比可分析吊重质量对摆角的影响。在试验中,采用两种不同质量的铝块与钢块作为吊重,绳长以及绳直径参数不变,分别做3次试验进行对比分析,得到平均动态响应对比曲线如图8所示。

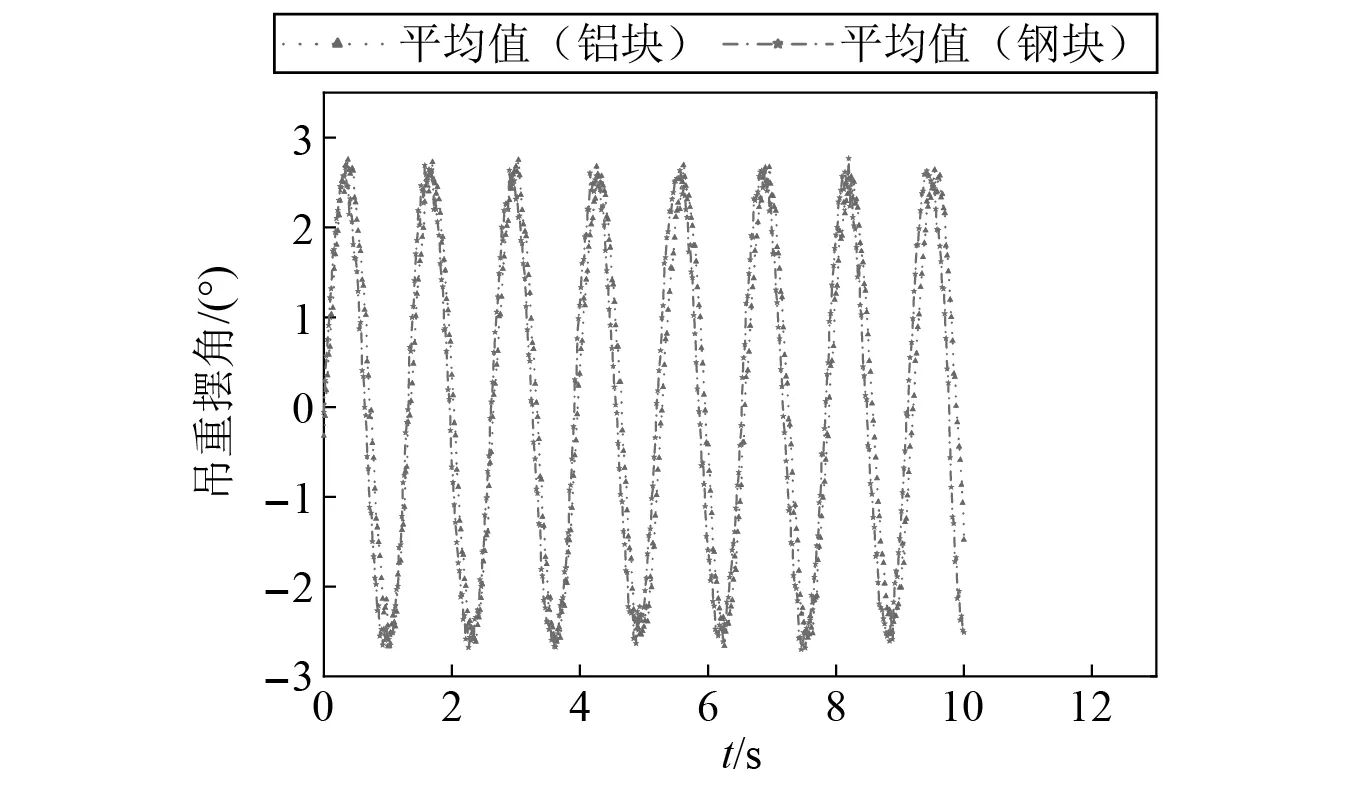
图8 质量对摆角动态响应的影响Fig.8 The influence of the load weight on dynamic response of the swing angle

由图8可知,当吊装质量从1.53 kg(铝块)增加到3.7 kg(钢块)时,摆角峰值呈现增加的态势,摆角周期则出现降低的趋势。为进一步定量分析吊重质量对吊装过程摆角的影响,本文汇总摆角的峰值与周期数据,如表8所示。由表8可知:当吊重质量增加时,摆角平均峰值由2.636°增加至2.670°,相对增加1.31%;而摆角周期平均值由1.305 s降低至1.293 s,相对下降0.92%。由此可以看出,吊重的质量变化会影响吊装过程的摆角响应,但影响幅度较小。

表8 质量对摆角影响对比(绳长438 mm,绳直径0.8 mm)Tab.8 Comparison of the influence of the load weight on the swing angle(Rope length 438 mm, rope diameter 0.8 mm)

3.3.2 绳刚度与阻尼对吊装系统动态响应的影响

在表5的试验设计中,试验f和试验g通过改变绳直径来改变绳刚度与阻尼系数,绳刚度增加会伴随着阻尼增加。本文中,分别对低刚度低阻尼(绳直径0.8 mm)与高刚度高阻尼(绳直径2 mm)两种工况进行了3次试验,进而分析绳刚度与阻尼对吊装系统动态响应变化的影响,得到两种工况下的摆角动态响应曲线如图9所示。

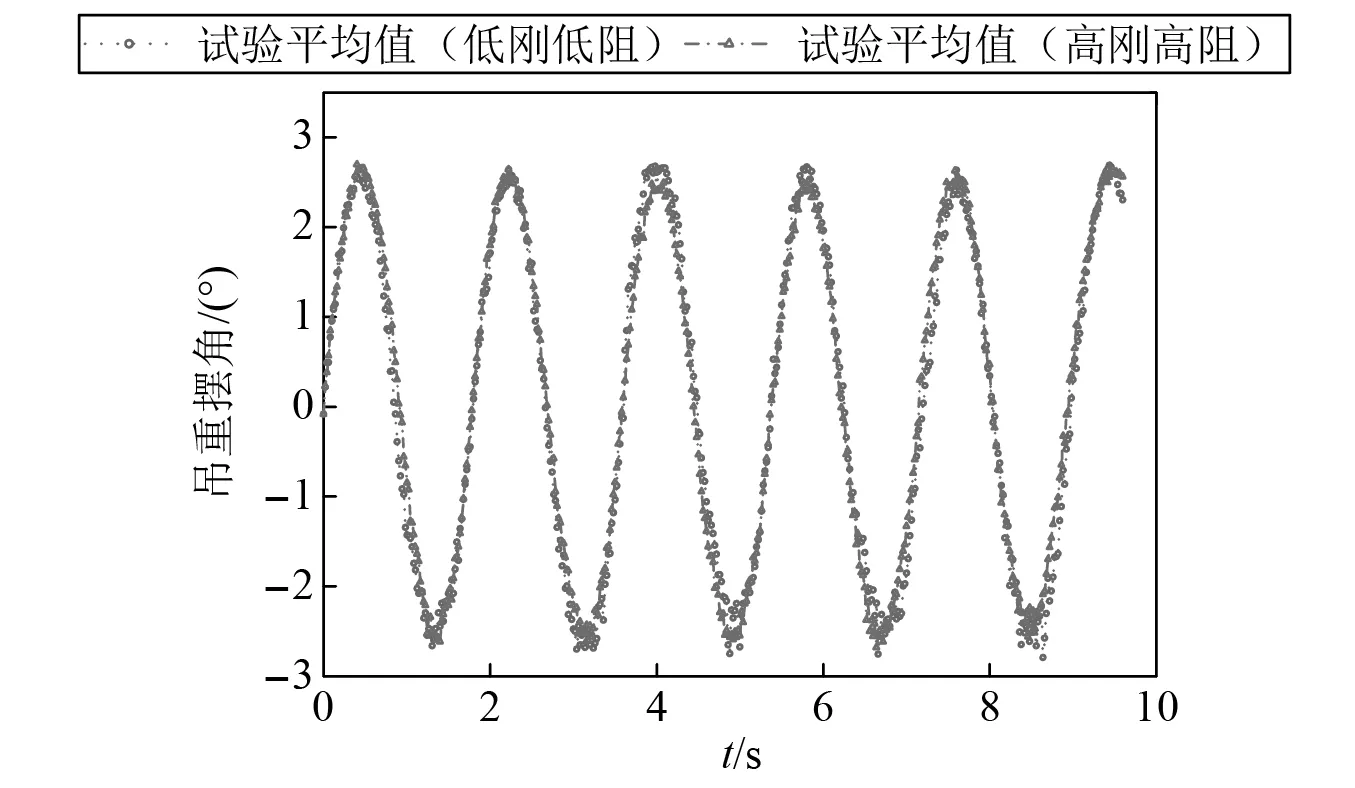
图9 刚度与阻尼对摆角动态响应的影响Fig.9 Influence of stiffness and damping on dynamic response of swing angle

由图9可知,当绳直径从0.8 mm增至2.0 mm时,绳参数的变化对吊重摆角的动态响应影响很小,吊重的摆角周期与摆角峰值相近。为进一步定量分析绳刚度和阻尼对吊重摆角的影响,本文汇总两种绳参数下吊重摆角与周期的试验结果,如表9所示。在表9中,低刚度低阻尼的摆角平均峰值(2.654°),相较高刚度高阻尼的摆角平均峰值(2.611°)变化1.65%,相应的摆角周期平均值变化0.84%。由此可进一步看出,绳参数的变化对于吊装系统吊重摆角动态响应的影响较小。