轮轨滑动对高速铁路扣件弹条振动特性的影响
2023-10-10陈光雄何俊华宋启峰
康 熙, 陈光雄, 何俊华, 宋启峰, 禄 盛
(1. 重庆邮电大学 先进制造工程学院,重庆 400065;2. 西南交通大学 机械工程学院 摩擦学研究所,成都 610031)
钢轨扣件是铁路轨道系统重要的组成部分之一,它将钢轨固定在轨枕或轨道板上。当扣件正常工作时,轨距被限定在合理的范围内,并且轮轨作用力可以正常传递到轨下结构中。扣件弹条断裂是一种常见的扣件失效形式,严重影响了列车的运行安全性和稳定性[1],该现象频繁出现于高铁[2]和地铁[3]线路中。高速列车运营速度较高,轮轨作用相对剧烈。在高铁线路上某些区段一旦出现大量扣件弹条断裂失效,将严重威胁到列车的行车安全。
对于扣件弹条断裂失效问题,学者们开展了大量的研究。Ling等[4]通过测试地铁车辆通过轨道时的动态响应,发现钢轨波磨激励的高频轮轨振动会加速扣件弹条的疲劳失效。余自若等[5]对X2型弹条扣件系统进行有限元建模,分析了扣压力、钢轨横向作用力、荷载频率对弹条疲劳失效的影响,发现过拧、钢轨横移会导致弹条疲劳寿命降低。Xiao等[6]通过仿真和试验研究了地铁e型弹条扣件失效机理,发现不恰当的安装方式是导致该型扣件失效的主要原因。此外,钢轨波磨激励的共振也可导致弹条断裂。Hasap等[7]通过有限元仿真和疲劳试验研究了扣件趾端载荷对e型弹条失效的影响,发现较低的趾端载荷可以减少冲击对弹条疲劳寿命的影响。高晓刚等[8]测试了轮轨耦合条件下SKL弹条的组装模态频率,通过锤击模态测试和有限元模态分析研究了预紧螺栓扭矩对弹条模态频率的影响,并对弹条结构进行优化以提高其疲劳寿命。崔树坤等[9]对W1型扣件弹条进行模态试验,研究了0~1 000 Hz频率内弹条的前2阶模态,分析了弹条安装状态对固有频率的影响。向俊等[10]基于有限元仿真,分析了WJ-7型扣件弹条的断裂机理,分别研究了前3阶车轮多边形磨耗、曲线半径、车速对弹条应力和疲劳寿命的影响,发现车轮多边形化、曲线半径减小、车速提高均会加速弹条疲劳失效。潘兵等[11]通过有限元瞬时动态仿真研究了轮轨滚滑接触对SKL15弹条失效的影响,发现轮轨间蠕滑力饱和引起的不稳定振动频率与弹条模态频率接近,可能导致弹条共振,加剧损伤。Wang等[12]分别测试了地铁列车经过钢轨波磨区段和无波磨区段时扣件弹条的振动加速度,通过建立车辆-轨道耦合模型,研究了波磨对扣件弹条振动和危险节点处应力的影响,发现钢轨波磨会引起弹条强迫振动,在一定的列车运行速度和波磨波长条件下,会引起弹条共振。基于有限元仿真和试验,Liu等[13]研究了e型和Fast型扣件弹条的失效现象,并对其疲劳寿命进行评估。研究发现,有限元仿真预测的扣件弹条损伤位置与现场测试结果基本一致。基于地铁列车-道床动力学模型,魏纲等研究了扣件失效对车轨系统动力响应的影响,发现扣件失效数量对车体加速度影响显著,对车体和衬砌的振动信号进行监测可辅助判定扣件失效位置。黄浩志等[14]建立了空心W1型弹条实体模型,对该弹条组装时的静力学表现和模态进行仿真计算,发现空心弹条的固有频率相比实心弹条显著提高。秦俊飞等[15]分别测试了地铁线路上行车激励下和无载状态下DI型扣件弹条的模态频率,发现行车激励下弹条模态频率相比无载状态下小幅减小。姜秀杰等[16]对行车载荷激励下ω型弹条的时域响应进行模拟,在实测路谱上叠加弹条组装模态频率,来模拟钢轨波磨激励下的弹条共振响应。研究发现,当波磨激励频率与弹条模态频率接近而引起共振时,弹条跟端应力增大,容易导致弹条断裂失效。刘玉涛等[17]建立了车辆-轨道垂向耦合系统动力学模型,分析了减振型无砟轨道同一道床板板端、板中和板尾扣件弹条的疲劳损伤差异性。仿真研究发现:应力循环幅值的增大导致了板端、板尾弹条的疲劳损伤平均值大幅增加。肖洪秀等[18]通过扫描电子显微镜对60Si2Mn材质弹条断口的宏观、微观形貌进行分析,发现疲劳源区的裂纹不平整,扩展区裂纹呈云浮状,瞬断区出现了明显韧窝现象。
高速列车在上下纵坡区段通常处于牵引或制动状态,当轮轨接触面之间存在水油污染时,在牵引或制动工况下可能发生轮轨滑动[19]。Cui等对京广线高速铁路钢轨波磨现象进行调查发现,在坡度为10.5‰的路段上存在严重的钢轨波磨和扣件弹条失效现象。进一步研究发现,轮轨滑动引起的摩擦自激振动为钢轨波磨的形成原因之一,但扣件弹条的失效机理尚不明确。
先前研究表明,特定频率的轮轨振动会引起弹条共振,加速其断裂失效。本文建立了车轮-钢轨-扣件系统有限元模型,采用复特征值分析求解轮轨滑动引起的不稳定振动频率和模态,发现轮轨饱和纵向蠕滑力引起的603 Hz不稳定振动可引起ω型扣件弹条共振。此外,该不稳定振动还可引起波长为130~190 mm的钢轨波磨。当车轮以300 km/h在波磨钢轨上滚动运行时,波磨激励的强迫振动可传递至扣件系统中,引起弹条共振。
1 有限元模型和理论模型
1.1 车轮-钢轨-扣件系统有限元模型
Cui等表明在京广线高速铁路测试区段内运营的列车类型为CRH3,在该区段内的平均运行车速为300 km/h。车轮踏面类型为S1002CN,车轮直径为0.92 m。该区段内轨枕间距为0.65 m,钢轨型面为CHN60。理想状态下,在直线线路或大半径曲线线路上,同一轮对左右车轮与钢轨间作用力非常相似。为了减少有限元模型中的网格数量,提高计算速度,在有限元软件ABAQUS中建立单轮-钢轨-扣件系统模型,如图1所示。模型网格单元类型均为C3D8I,车轮与钢轨接触区域的网格被细化,以提高仿真精度。轮轨接触区内车轮网格尺寸约为13 mm×13 mm×10 mm,钢轨网格尺寸约为5 mm×5 mm×7 mm。在车轮中心处建立参考点,将该点与车轮-车轴接触区域的表面耦合,并将一系悬挂力施加到该点上。钢轨长度为36.252 m,以避免端部固定对计算结果的影响。模型中共有8个WJ-7型扣件系统,其他区域的轨下结构支撑刚度和阻尼采用7×7矩阵型“接地”弹簧和阻尼单元模拟。扣件弹条跟端与铁垫板的支座接触,铁垫板的下表面被固定。在平垫片上表面的耦合点处施加扣件预紧力,将垫片下压在弹条顶端。受到扣件预紧力的作用,弹条趾端将绝缘块压紧在钢轨上,钢轨底部被轨下垫板支撑。为了提高仿真计算可行性和运算速度,在扣件系统有限元模型中简化了螺栓、螺母和铁垫板的结构,将单个轨下垫板简化为3×3矩阵型“点对点”弹簧和阻尼单元。车轮与钢轨、钢轨与绝缘块、弹条顶端与平垫片、弹条跟端与铁垫板、弹条趾端与绝缘块之间的切向接触关系为“罚”摩擦公式,法向接触关系为“硬”接触。接触类型为“面-面”接触,滑移类型为“有限滑移”。该模型的主要参数和材料属性[20-21]分别如表1和表2所示。

表1 车轮-钢轨-扣件系统有限元模型主要参数

表2 车轮-钢轨-扣件系统有限元模型材料属性
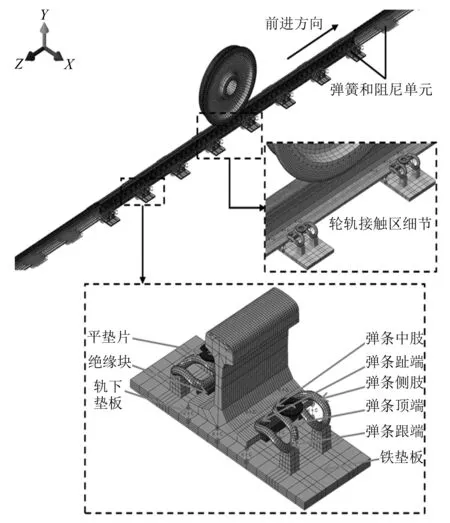
图1 车轮-钢轨-扣件系统有限元模型Fig.1 Finite element model of a wheel-rail-fasteners system
1.2 扣件预紧力选取
在扣件弹条振动特性的仿真研究中,扣件系统参数的合理选取十分关键。为了选取合适的扣件预紧力,利用车轮-钢轨-扣件系统有限元模型对扣件系统的受力状态进行模拟。从扣件系统静力学分析结果中提取了不同扣件预紧力状态下扣件扣压力和中肢位移,并与安装规范进行对比,如表3所示。当扣件预紧力为26 kN时,扣压力满足规范要求,中肢位移与标准范围相差约8.1%。因此,当选取扣件预紧力为26 kN及以上时,扣件系统模型可以满足仿真分析需要,仿真中的扣件预紧力取为26 kN。

表3 扣件系统模型验证Tab.3 Verification of the fastener system model
1.3 摩擦自激振动的复特征值分析法
在ABAQUS软件中将车轮和钢轨模型划分网格,不考虑轮轨摩擦力作用下系统的运动平衡方程[22]为
(1)
式中:M,C,K分别为系统的质量、阻尼、刚度矩阵;x为节点在平衡位置处的位移向量。
在雨雪天气以及轮轨间存在污染物的情况下,高速列车在上下陡坡区段牵引或制动时,轮轨间的牵引力或制动力可能达到最大黏着力,从而引起轮轨滑动[23]。此时,轮轨间的纵向蠕滑力趋于饱和,其大小约为轮轨间法向接触力乘以摩擦因数,即
Ff=μKN
(2)
式中:Ff为轮轨间摩擦力;N为轮轨间法向接触力;μK为动摩擦因数。在仿真中考虑了轮轨摩擦力-相对滑动速度负斜率曲线[24]的影响,假定动摩擦因数的计算公式为
μK=0.2+(0.3-0.2)e-0.011VS
(3)
式中,VS为轮轨间相对滑动速度。
摩擦力作用下轮轨系统简化后的运动方程由式(1)变为
(4)
式中,MD,CD,KD分别为存在扰动力时系统的质量、阻尼、刚度非对称矩阵。式(4)对应的特征方程为
(MDλ2+CDλ+KD)φ=0
(5)
式中:λ为特征值;φ为特征向量。根据子空间投影法和QZ法求解该方程,其通解为
(6)
式中:t为时间;αi为特征值实部;ωi为特征值虚部; j为虚部单位。由式(6)可知,当特征值实部大于0时,节点位移随时间逐渐增大,轮轨系统趋于不稳定。
通常采用等效阻尼比ξ来评价系统稳定性,其定义为
ξ=-2αi/(|ωi|)
(7)
当特征值实部大于0时,等效阻尼比为负数,系统可能产生不稳定振动。并且,特征值实部越大,等效阻尼比越小,对应不稳定振动的发生趋势越强。
2 计算结果
2.1 轮轨滑动对扣件弹条共振的影响
在频率范围0~1 200 Hz内,通过复特征值分析可获得轮轨间饱和纵向蠕滑力作用下系统摩擦自激振动在频域内的分布,如图2(a)所示。由图2(a)可知,轮轨系统仅存在603 Hz的不稳定振动。潘兵等通过瞬时动态分析获得了轮轨滚滑接触工况下钢轨表面测点处的垂向振动加速度,发现轮轨系统存在约609 Hz的不稳定振动,这与本文采用复特征值分析预测的结果基本一致,在一定程度上验证了仿真结果的有效性。

图2 不稳定振动的分布和模态Fig.2 Distribution and mode shape of unstable vibrations
603 Hz的不稳定振动模态,如图2(b)所示。从振动模态可以看出,车轮和扣件弹条上均发生了明显变形,这表明轮轨系统不稳定振动可传递到扣件系统中。刘旭铁的研究模态分析表明,标准安装状态下该型扣件弹条在0~1 200 Hz内共有3阶模态,频率分别为570.68 Hz,640.73 Hz和652.78 Hz。其中,弹条第3阶模态振型为弹条2个侧肢以弹条跟端和趾端为支点,沿轨道方向对称外翻振动,这与图2(b)中603 Hz不稳定振动发生时弹条的变形情况相似。并且,该不稳定振动频率与弹条第3阶模态频率相对误差约为7.6%,这可能是由于车轮重力和一系垂向悬挂力引起扣件垂向变形,进而引起弹条约束状态及扣压力不同于标准安装状态,从而导致弹条组装模态频率减小。因此,轮轨滑动引起的603 Hz不稳定振动激励了扣件弹条第3阶模态,引起共振,加剧弹条损伤。
2.2 轮轨滑动引起的钢轨波磨对扣件弹条共振的影响
Cui等指出京广线高速铁路某纵坡区段钢轨波磨的典型波长范围为130~190 mm,并且,在该区段内部分扣件系统的弹条较新,如图3所示。这表明部分弹条发生了断裂失效,从而被重新更换。进一步研究表明,轮轨滑动引起的约607 Hz的不稳定振动是该区段钢轨波磨形成的原因之一,该振动频率与本文仿真结果中603 Hz的不稳定振动频率非常接近。

图3 钢轨波磨和较新的扣件弹条Fig.3 Rail corrugation and newer fastener clips
为了进一步研究轮轨滑动引起的钢轨波磨对扣件弹条振动特性的影响,建立车轮-钢轨-扣件系统瞬时动态模型。在车轮上施加转动速度和平移速度,模拟轮轨滚动接触工况,如图4所示。为了降低计算量以节省计算时间,动态模型中车轮为刚性体,单元类型为R3D4,钢轨、扣件弹条等其他模型与图1所示的有限元模型参数相同。通过重新编译钢轨表面节点坐标[25],模拟了钢轨波磨真实廓形。波磨波长初始值为线路实测典型波磨波长的平均值160 mm,波深H分别取为0.05 mm,0.07 mm,0.09 mm(为了显示清晰,图4中波磨的波深为3 mm),波磨廓线方程为

图4 车轮-钢轨-扣件系统瞬时动态模型Fig.4 Transient dynamic model of a wheel-rail-fasteners system
y-y0=0.5H{cos[π(z-z0)/80]-1}
(8)
式中:z0,y0为波磨区段钢轨表面初始节点在ZY平面内的坐标;z,y为其他节点的坐标。车轮以300 km/h的速度在钢轨上滚动运行4.55 m,波磨区段总长为0.8 m。车轮在运行至波磨区段之前,先经过约1.2 m的动态松弛区,以降低轮轨接触状态由静到动产生激扰的影响。
计算了钢轨无波磨和存在波磨工况下,仿真关注区域内轮轨间法向接触力随时间的变化情况和功率谱密度(power spectral density, PSD)分析结果,如图5所示。由图5可知,相比无波磨工况,当车轮通过波磨区段时,轮轨间法向接触力波动加剧。由轮轨间法向接触力的PSD分析结果可知,钢轨波磨激励轮轨系统产生约521 Hz的振动主频,并且振动强度随着波深增加而增大。
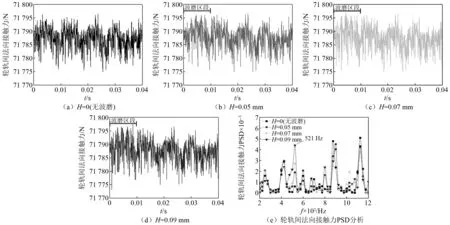
图5 钢轨波磨对轮轨间法向接触力的影响Fig.5 Effect of rail corrugation on wheel-rail normal contact forces
为了研究钢轨波磨激励的强迫振动在扣件系统中的传递情况,进一步提取图4中扣件弹条趾端中心节点A的垂向振动加速度,并进行PSD分析,重点关注扣件弹条的前3阶模态频率范围570~653 Hz的振动情况,如图6所示。由图6可知,随着波磨波深的逐渐增加,弹条节点A在580~640 Hz内的振动幅值不断增大。这个振动峰值与弹条前3阶模态频率范围部分重合,可引起弹条共振。因此,当列车通过波磨区段时,即使不发生轮轨滑动,钢轨波磨激励的轮轨强迫振动也可引起扣件弹条共振。此外,由于仿真中轮轨接触状态由静态变为动态时会产生初始激扰,虽然设置了动态松弛区,但仍无法完全消除初始激扰引起的振动,导致轮轨法向接触力(见图5(e))和扣件弹条节点A(见图6(e))出现多处显著的能量聚集,尤其在700 Hz以上的高频区。因此,当前模型难以准确分析钢轨波磨是否会激励弹条更高阶模态。在后续的研究中,将对该模型进行改善,降低轮轨接触状态变化引起的初始激扰的影响,进一步分析钢轨波磨对弹条更高阶模态的激励作用。

图6 钢轨波磨波深对弹条节点A垂向振动加速度的影响Fig.6 Effect of amplitudes ofrail corrugation on vertical vibration acceleration of clip node A
进一步研究不同波长钢轨波磨对扣件弹条模态的激励作用,分别计算了波磨波长λ为130 mm和190 mm、波深均为0.09 mm工况下扣件弹条趾端中心节点A的垂向振动加速度PSD分析结果,如图7所示。由图7可知,当波磨波长为160 mm和190 mm时,弹条节点在580~640 Hz内均存在峰值,可能引起弹条共振。此外,当波磨波长为130 mm时,弹条节点A在550 Hz频率处存在峰值。虽然该振动频率略低于弹条的前3阶模态频率范围下限570 Hz,但由于行车激励可导致弹条部分组装模态频率减小,因此波长为130 mm的钢轨波磨激励的强迫振动也可能引起弹条共振。
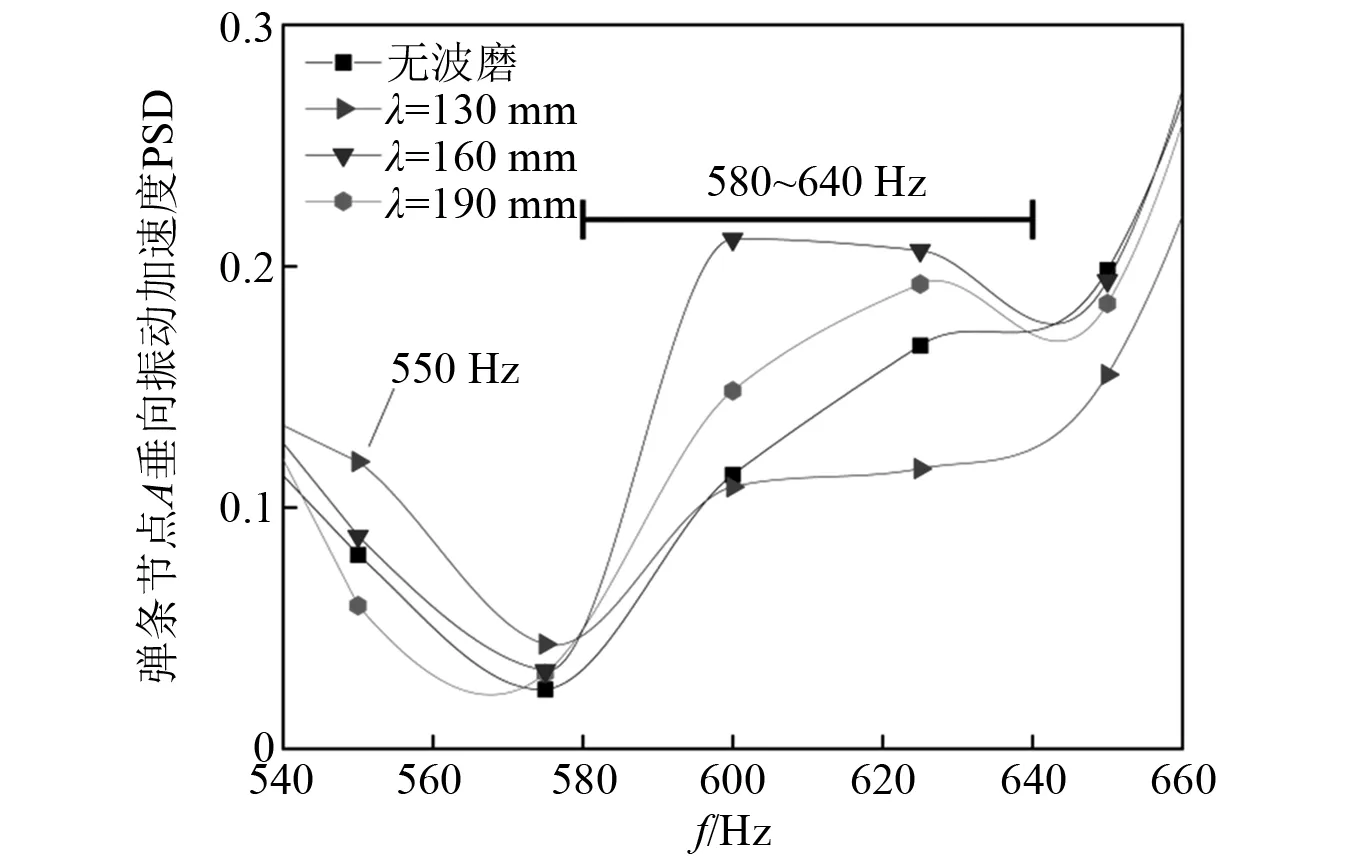
图7 钢轨波磨波长对弹条节点A垂向振动加速度的影响Fig.7 Effect of wavelengthsof rail corrugation on vertical vibration acceleration of clip node A
以上分析表明,轮轨饱和纵向蠕滑力引起的603 Hz不稳定振动可通过引发特定波长的钢轨波磨,激励与扣件弹条前3阶组装模态频率接近的轮轨振动,传递到扣件系统中,引起弹条共振,加速其失效。
3 影响因素分析
3.1 轨下垫板刚度的影响
在轨下垫板的静刚度设计值主要是根据轨道部件允许应力和变形确定的,本文仿真模型中采用的扣件系统轨下垫板静刚度设计值范围为20~30 MN/m[26]。但由于扣件类型、环境温度和材料老化等因素的影响,轨下垫板的刚度值在服役期间会发生变化[27]。为了分析不同轨下垫板刚度对扣件弹条共振的影响,计算了轮轨滑动引起的603 Hz不稳定振动对应的等效阻尼比随轨下垫板刚度的变化情况,轨下垫板刚度范围为15~35 MN/m,如图8所示。根据等效阻尼比可以评估轮轨系统摩擦自激振动的发生趋势,603 Hz不稳定振动对应的等效阻尼比越小,扣件弹条发生共振的可能性越高。由图8可知,等效阻尼比随着轨下垫板刚度的增大先减小后增大,但整体变化较小。
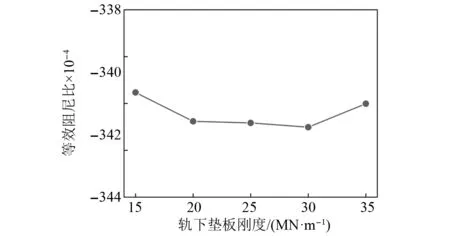
图8 轨下垫板刚度的影响Fig.8 Effect of stiffness of rail pads
3.2 扣件预紧力的影响
对不同预紧力工况下车轮-钢轨-扣件系统的稳定性进行分析,重点关注603 Hz不稳定振动的发生趋势。仿真中扣件预紧力范围为25~29 kN,该不稳定振动对应的等效阻尼比如图9所示。由图9可知,扣件预紧力的变化对等效阻尼比的影响相对较小。

图9 扣件预紧力的影响Fig.9 Effect of fastener preload
4 结 论
(1) 当轮轨接触面之间存在污染物,高速列车在上下纵坡区段牵引或制动时,饱和纵向轮轨蠕滑力引起的约603 Hz不稳定振动与扣件弹条第3阶模态频率接近,可引起共振,加速弹条失效。
(2) 轮轨滑动引起的603 Hz不稳定振动可导致高铁线路纵坡区段钢轨波磨的形成,当列车以300 km/h的车速通过此区段时,即使轮轨间不发生滑动,钢轨波磨激励的轮轨强迫振动也可引起扣件弹条共振。
(3) 轨下垫板静刚度、扣件预紧力对轮轨滑动引起的603 Hz不稳定振动的发生率整体影响较小。
在未来工作中,将采用线路试验对结论进行验证。此外,在下一步工作中,将考虑通过改善扣件弹条结构以改变其固有频率,从而避免共振的发生。
