悬垂立管波致疲劳与流致涡激振动疲劳特性研究
2023-10-10梁天纬许玉旺付世晓任浩杰张萌萌
梁天纬, 许玉旺, 付世晓, 任浩杰, 张萌萌, 宋 斌
(1. 上海交通大学 海洋工程国家重点实验室, 上海 200240; 2. 上海交通大学 船舶海洋与建筑工程学院, 上海 200240;3. 高新船舶与深海开发装备协同创新中心, 上海 200240; 4. 上海交通大学 极地深海技术研究院, 上海 200240)
悬垂立管是应用于可移动式养殖工船[1]以及温差能发电平台冷海水提升系统[2]中的一种特殊立管结构,其将较深层低温洁净海水输送至船体或平台内,进行冷海水高经济价值鱼类养殖或利用与表层海水的温差发电作业。不同于钢悬链式、顶张力式等常见立管结构形式,其一端与平台连接,另一端完全自由,在复杂的海洋环境作用下将产生更复杂的动力响应,在其设计流程中,疲劳分析是至关重要的一环。
按产生原因分类,立管的疲劳损伤主要可分为波致疲劳损伤与涡激振动(vortex induced vibration,VIV)疲劳损伤:波致疲劳损伤是立管在波浪载荷以及顶部连接平台运动的作用下产生的;涡激振动疲劳损伤则是在来流作用下,立管两侧形成交替泄涡诱发的涡激振动导致的。
国内外已有大量学者对常见立管形式的疲劳特性进行了研究。在波致疲劳方面,Sheehan等[3]对比了统计分析与确定性分析两种疲劳损伤分析方法在柔性立管上的应用,并证明了确定性分析方法的有效性;朱东华[4]采用有限元频域计算方法研究了钢悬链立管的波致疲劳特点,发现波致疲劳与有义波高密切相关,疲劳损伤随着有义波高的增加呈指数型增长。对于涡激振动疲劳,目前的研究主要针对于两端约束的立管,如顶张式立管和刚悬链线立管等:王琳等[5]针对两端铰支的海洋立管提出一种二维等效涡激振动数值模拟模型,研究了海流速度和壁厚对立管疲劳寿命的影响,发现壁厚增加会使立管疲劳寿命延长;高云等[6]结合水池试验,研究了细长柔性立管涡激振动响应的特点,并对比了频域与时域法所得涡激振动疲劳损伤的差别;还有其他学者对钢悬链线式与顶张力式立管[7-9]的涡激振动疲劳损伤特性与分析方法进行了研究。关于两种疲劳的对比,刘泽光[10]基于规范,应用数值分析方法对FDPSO钻井隔水管的波致疲劳与涡激振动疲劳进行了一定的分析,发现在管不同截面位置,两种疲劳损伤占比不同。
然而,悬垂立管作为一种特殊立管结构,其疲劳损伤响应特性学术界尚缺乏系统性的研究:Gao等[11]提出时-频混合疲劳分析方法,研究了不同海况下悬垂管的波致疲劳寿命;吴天昊等[12-13]通过水池试验探究了平台运动作用下悬垂立管的涡激振动响应以及涡激振动疲劳特性。但目前业界对于悬垂立管波致疲劳与涡激振动疲劳的特性依旧缺乏更深的分析。
为了能够进一步深入了解悬垂管的疲劳特性,本文对一根安装于可移动式深海养殖工船的大直径悬垂取水管进行疲劳分析。由于当前国内外尚未有相关分析理论或软件能实现立管波致振动和流致涡激振动耦合响应分析,且在工程设计(基于DNV以及API等规范)与学术研究中也一般采用解耦分析方法进行处理,本文考虑工作海域海况分布概率,采用解耦方法分别计算了立管的波致疲劳与涡激振动诱导疲劳损伤,对比分析了两者疲劳损伤的敏感参数、积累速度以及分布特点,并为将来波流联合作用下悬垂立管总体动力与涡激振动耦合响应分析和疲劳强度校核提供对照依据。
1 数学模型
1.1 波浪作用下立管动力响应时域计算方法
本文建立了养殖工船船体、悬垂立管以及系泊系统的全耦合计算模型,求解在波浪作用下取水立管的动力响应,整个系统的运动控制方程可写为
{FShip(t)}+{FMooring(t)}+{FRiser(t)}
(1)
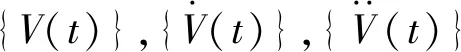
对于取水立管这类细长杆件结构,其单位长度上所受的浪流载荷可以通过Morison方程进行计算
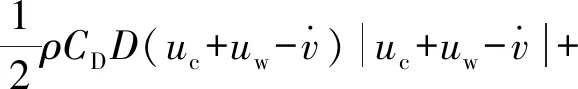
(2)
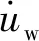
通过求解以上方程,可以获得立管的动力响应,继而采用雨流计数法求解最终的立管波致疲劳损伤。
1.2 立管流致涡激振动响应分析方法
目前对涡激振动响应的预报,主要可分为计算流体力学方法、基于尾流振子模型的预报方法以及基于半经验载荷系数模型的预报方法。本文采用工程上广泛应用的半经验载荷系数模型预报方法对取水管的涡激振动响应进行双向(IL顺流方向(in-line,IL)与横流方向(cross-flow,CF))频域预报,其预报流程为:
(1)求解立管系统的固有频率与振型。
(2)基于流速的分布以及式(3)的斯特劳哈尔关系判断立管涡激CF方向上振动的潜在激发模态
(3)
式中:St为斯特劳哈尔数,受立管雷诺数与粗糙度影响;U为流速。
(3)对潜在激发模态的能量进行求解排序,确立最终CF方向上涡激振动的激发模态和各个模态沿管长激励区与阻尼区分布。
(4)将Gopalkrishnan[15]试验获得的刚性圆柱水动力系数进行适应性修正后,作为输入参数,通过能量平衡迭代的方法,求解出立管CF方向各阶激发模态的响应幅值。
(5)假定IL方向的涡激振动响应频率始终为CF方向的2倍,确定IL方向涡激振动频率。
(6)通过相同的方法,采用Soni等[16]所得的水动力系数作为输入参数,求得立管IL方向的涡激振动响应。
因剪切流下的立管涡激振动往往是多频响应,且立管上部分点的应变由IL与CF方向涡激振动同时作用产生,故在基于频域预报方法求解双向涡激振动诱导结构疲劳损伤时,先对IL与CF方向上的每一阶激发模态赋予一个随机相位,进而可得到立管上各点的响应时历,最后使用雨流计数法求解立管的涡激振动疲劳损伤。
1.3 S-N曲线
养殖工船所采用的取水管材料为标准材料钢,在各个船级社的规范中能查取到基于大量试验数据拟合绘制得到的S-N曲线。本文采用挪威船级社(DNV)的疲劳分析规范[17]中,用于钢质结构在海水中无腐蚀保护条件下的S-N曲线,如表 1所示,并选择其中的C1曲线进行计算,如图 1所示。

表1 DNV RP-C203海水自由腐蚀下钢质S-N曲线参数表
2 数值计算
2.1 数值计算模型
养殖工船全系统的结构示意如图 2所示,包含可移动式养殖工船船体、悬垂立管以及系泊系统共三部分,图 3为对应的数值计算模型。
系统中各个主要结构的尺寸参数如表 2所示。

表2 数值计算模型主要尺寸参数
取水管选用美国石油协会的行业标准(API-5L)中外径0.914 m、壁厚0.015 9 m的标准尺寸钢管。在数值计算过程中,假设取水管沿长度方向外径一致,全管密度均匀,即忽略钢管管节连接点和其他实际中可能包含的管体附件对取水管外径与质量的影响。分析中不考虑管内流的影响,取水管内外为密度相同的海水。基于以上假设,简化后的取水管模型力学性能参数如表3所示。

表3 取水管力学性能参数Tab.3 Mechanical properties of the riser
海洋工程中的立管与平台连接处会安装特殊的保护或缓冲结构,来缓解连接处的应力集中和疲劳问题。在数值计算中为了提高计算效率,利于结果的收敛,将计算模型中的立管与平台定义为铰接,并约束绕管中轴线的转动自由度,使风浪流作用下平台的六自由度运动中仅有平动传递至立管连接点。这种简化与工程上所采用的球铰型立管连接器在功能上是一致的。
2.2 数值计算环境参数
2.2.1 波浪参数
波浪环境是影响波致疲劳损伤的主要参数,根据设计校核规范的要求,本文基于此养殖工船作业附近海域全年波浪散布图数据进行取水管波致疲劳损伤的计算分析,其分布概率数据如图 4所示,波浪谱选用Jonswap谱。在概率分布图中共有36组波高周期组合的海况出现概率不为零,需全部进行计算后,将结果按对应海况出现概率进行加权处理求解最后总的波致疲劳损伤积累情况。在计算各个海况下波致疲劳损伤时,每个工况计算时长为4 h,前1 h用于系统稳定,取后3 h的响应作为雨流计数法输入,开展疲劳分析。
2.2.2 洋流参数
本文主要考虑海流所导致的立管涡激振动,由于所分析的可移动式养殖工船为单链单点系泊,具有良好的风标效应,使得船体在大多数时间里总是保持迎流姿态,因此可以假设海流相对于取水管的流向在作业时不发生变化且流向不随海水深度发生变化。这种定常海流,将导致立管产生稳定的涡激振动,使得立管上疲劳积累位置更集中,基于这种假设的疲劳计算结果更为保守。本文选取一年重现期的海流剖面,假设在不同表层流速下,流剖面的分布情况是相同的,其海流剖面分布如图 5所示,计算所用全年表层流速的分布概率如图 6所示。计算时取每个表层流速区间的最大流速计算,其所得全年涡激振动疲劳损伤乘以相应流速区间出现的概率,最终求和得到立管全年流致涡激振动疲劳损伤积累情况。
2.3 数值计算流程
在进行波致疲劳分析时,分别通过三维势流理论以及莫里森方程计算养殖工船以及系泊链与取水管在波浪作用下的水动力载荷,养殖工船视为刚体处理,系泊链与取水管则采用有限元法,考虑系泊链、取水管与船体在连接点处的力的传递,构建并求解该全耦合系统的时域运动响应方程。这部分计算工作在海洋工程水动力软件ORCAFLEX软件中进行,其中,取水管与系泊链分别划分为300个单元与500个单元。
涡激振动疲劳损伤的计算方法在业界获得广泛认可的是SHAER7与VIVANA。为了后期能进一步从时域进行涡激振动响应的数值分析,本文采用VIVANA进行了取水管涡激振动响应的预报与疲劳计算。为保持一致性,将取水管同样划分为300个单元进行分析。
VIVANA经过数代的发展更新,已能有较为良好的频域涡激振动预报结果。以Lu等[18]所进行的剪切流涡激振动试验与预报结果为例(具体立管模型参数与流场信息参见其文章),应用VIVANA涡激振动预报程序进行建模分析。立管涡激振动响应均方根(root mean square,RMS)值的预报结果与Lu等研究的结果绘制如图 7所示。通过对比,可以发现本文所采用的涡激振动数值预报结果具有较好的精度。
3 结果分析与讨论
在立管同一个运动周期内,立管截面同方向内壁上的应力变化幅值总是小于外壁的,故本文在进行疲劳分析时,同一截面上选取外侧间隔45°的8个点,提取对应的MISES应力进行疲劳损伤分析,选取其中疲劳损伤最严重的结果作为立管长度方向上在此处的疲劳损伤计算结果。
对截面上的8个分析点按如图8方式进行编号定义,在初始时刻,点1与点5的连线与来流方向相同,定义为顺流方向(IL),点3与点7的连线与来流方向垂直,定义为横流方向(CF)。
3.1 波致疲劳计算结果
取波浪散布图中,最缓和、最恶劣以及出现概率最高的海况,分析立管波致疲劳损伤分布并乘以相应海况出现的概率,绘制得到损伤分布贡献如图9所示。图9(a)~图9(c)分别为在有义波高0.5 m,1.0 m与8.0 m,对应特征周期2.5 s,7.0 s与18.0 s的海况下,立管全年疲劳积累沿长度与截面角度的分布情况。在不同海况下,立管的波致疲劳损伤在截面上的分布特征是相同的,原因是船体风标效应的存在,使得在大部分时间里,船体总是保持迎浪姿态,纵摇运动远比横摇运动激烈,立管受平台运动以及浪流载荷直接作用的方向也相对固定,IL方向上的疲劳损伤更为严重。
在相同特征周期、不同有义波高的海况下,立管管长方向全年最大波致疲劳损伤分布如图10所示。在相同特征周期下,海浪谱有义波高的变化不会对立管波致疲劳损伤在立管方向上的分布情况产生影响;但立管波致疲劳损伤的积累速度则与海浪谱有义波高明显相关:有义波高数值越大,立管的疲劳损伤积累速度越快,即疲劳寿命越短。
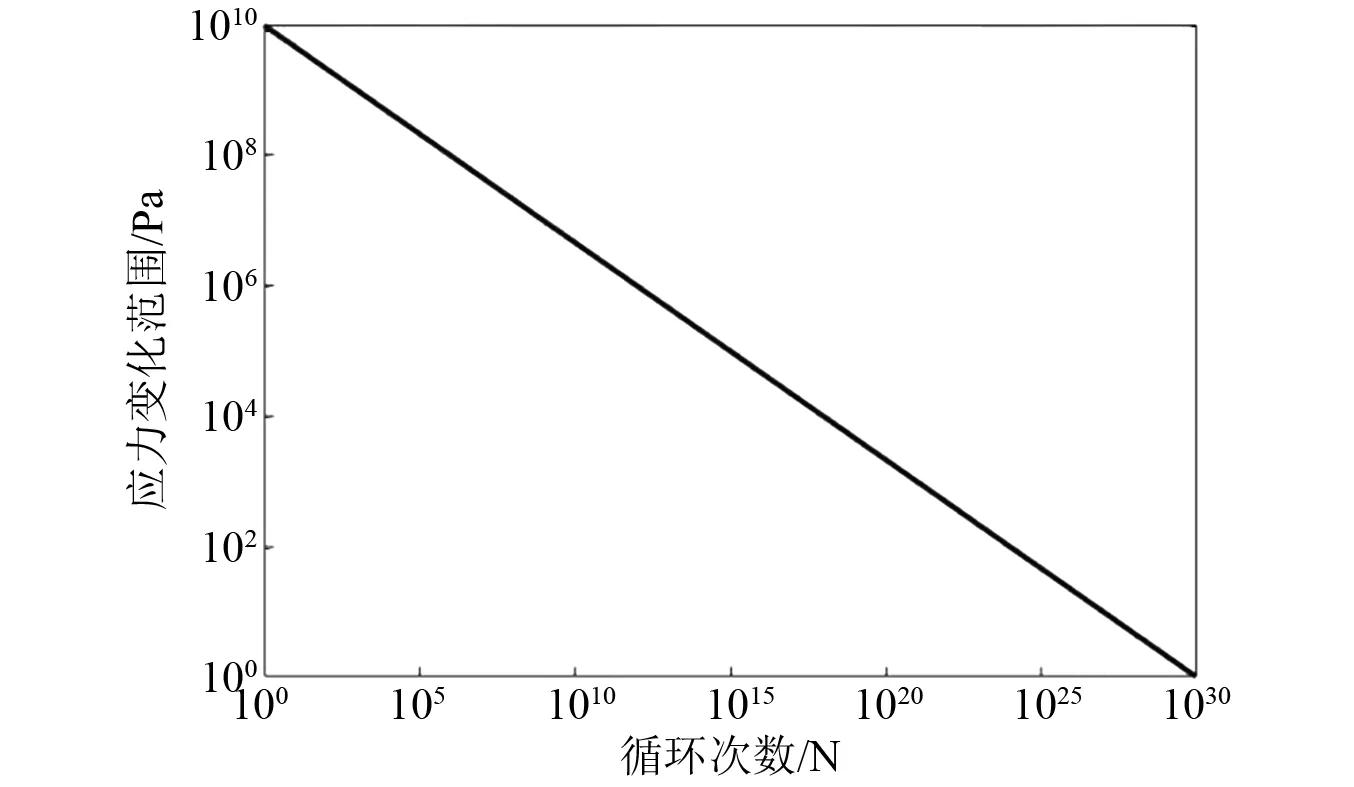
图1 海水自由腐蚀下的S-N曲线C1Fig.1 S-N curves C1 in seawater for free corrosion
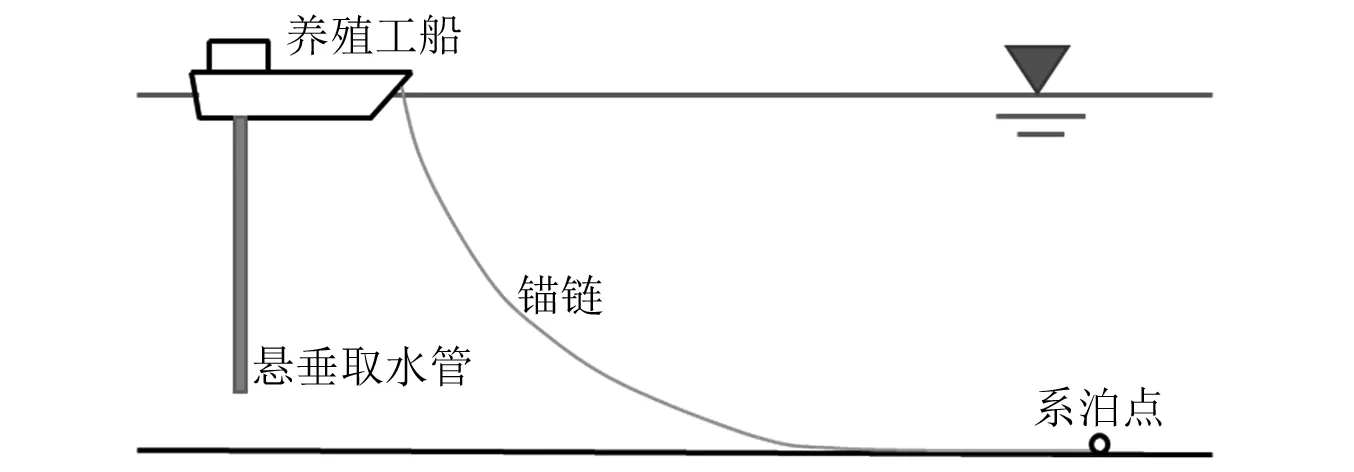
图2 整体结构示意图Fig.2 Schematic diagram of structure

图3 数值计算模型Fig.3 Numerical calculation model
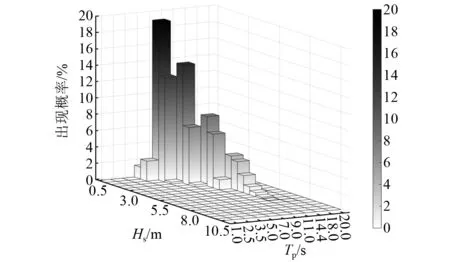
图4 不同海况出现概率Fig.4 Wave distribution probability
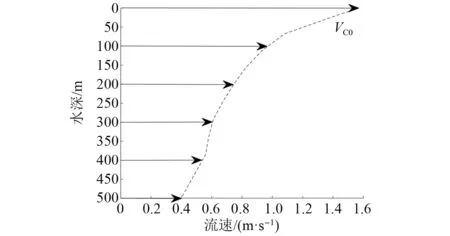
图5 一年一遇流剖面分布情况Fig.5 Current profile for 1-year return period
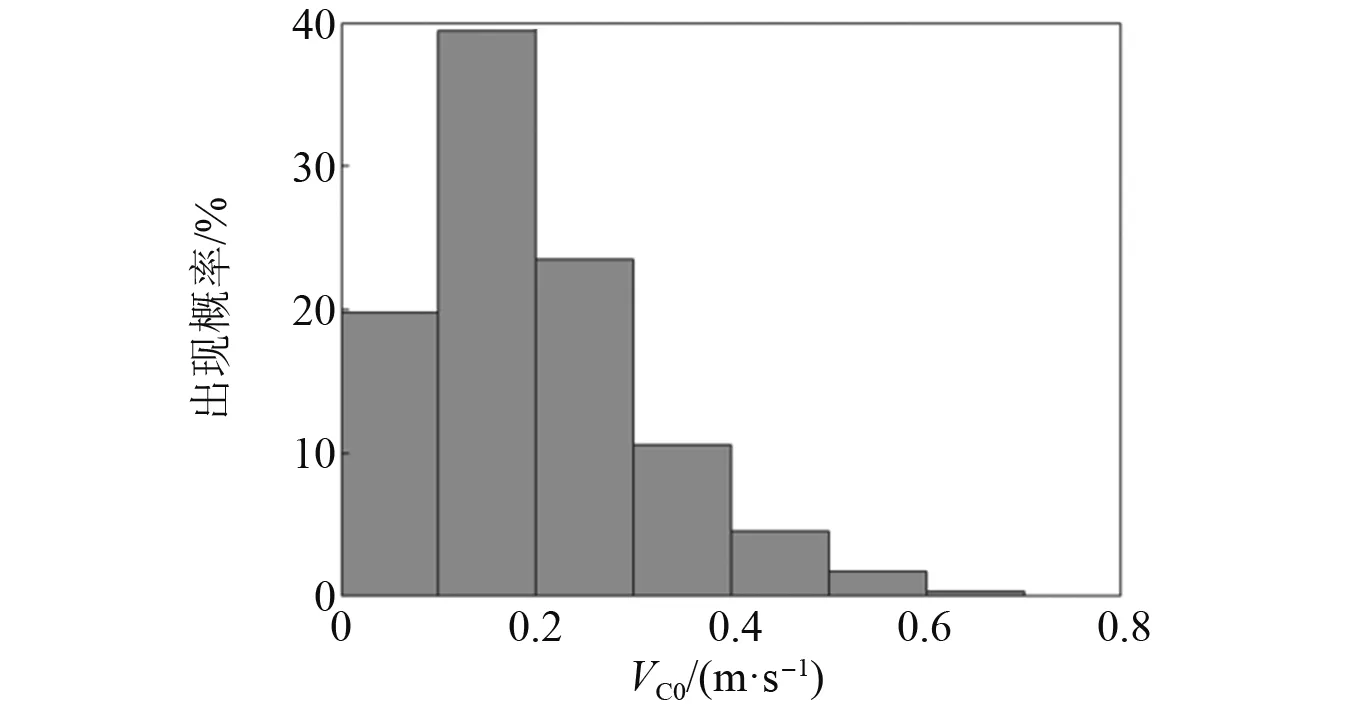
图6 表层流速分布概率Fig.6 Distribution probability of the surface current velocity

图10 同特征周期海况下立管管长方向截面最大波致疲劳损伤分布Fig.10 The most serious wave-induced fatigue damage of the cross section distribution along the length with the same Tp
在相同有义波高、不同特征周期的海况下,立管管长方向全年最大波致疲劳损伤分布如图11所示。当保持海浪谱有义波高不变时,特征周期的变化会显著影响立管波致疲劳损伤沿管长的分布情况,且对应的疲劳损伤积累速度也会发生相应的改变。这是由于特征周期变化使得对应不规则波中波浪周期的组成成分发生改变,与船体的某阶固有频率相近导致船体的运动更加剧烈或与立管的某阶固有频率相近,导致立管对应阶的模态响应更加剧烈,这都将影响波致疲劳沿管长的分布。
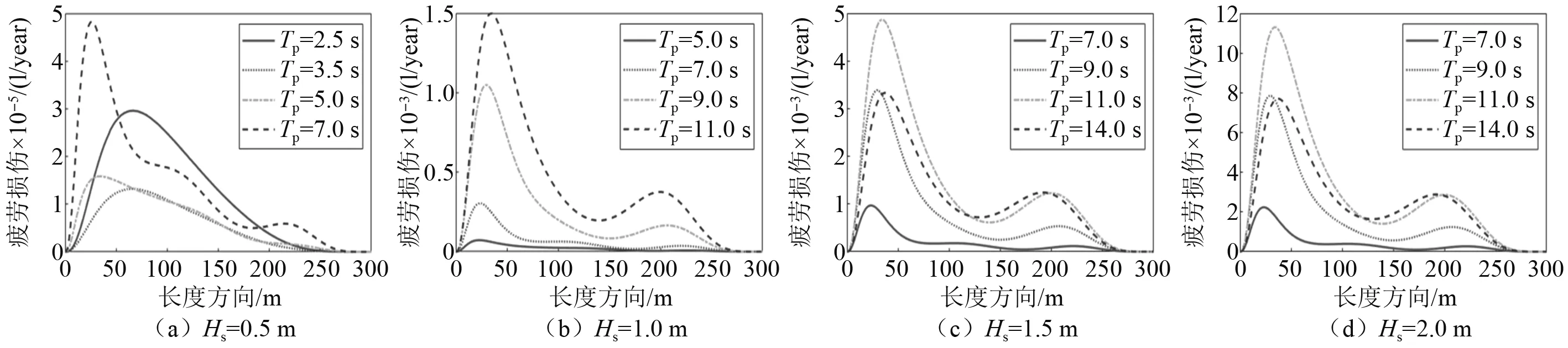
图11 同有义波高海况下立管管长方向截面最大波致疲劳损伤分布Fig.11 The most serious wave-induced fatigue damage of the cross section distribution along the length with the same Hs
3.2 流致涡激疲劳计算结果
基于半经验载荷系数模型的频域预报方法以立管结构涡激振动的“锁定”现象为基础,本文所分析的悬垂立管模态信息如图12与图13所示。 图14为不同表层流速下立管的涡激振动激发频率。立管在剪切流下为多频响应,分为主导频率和其他频率。在现行的频域涡激振动预报软件中,总是认为IL方向的涡激振动激发频率为CF方向的两倍,在所有计算工况中,立管CF方向上的最高激发模态不超过4阶,主导模态不超过3阶,IL方向上的最高激发模态不超过6阶,主导模态不超过5阶。
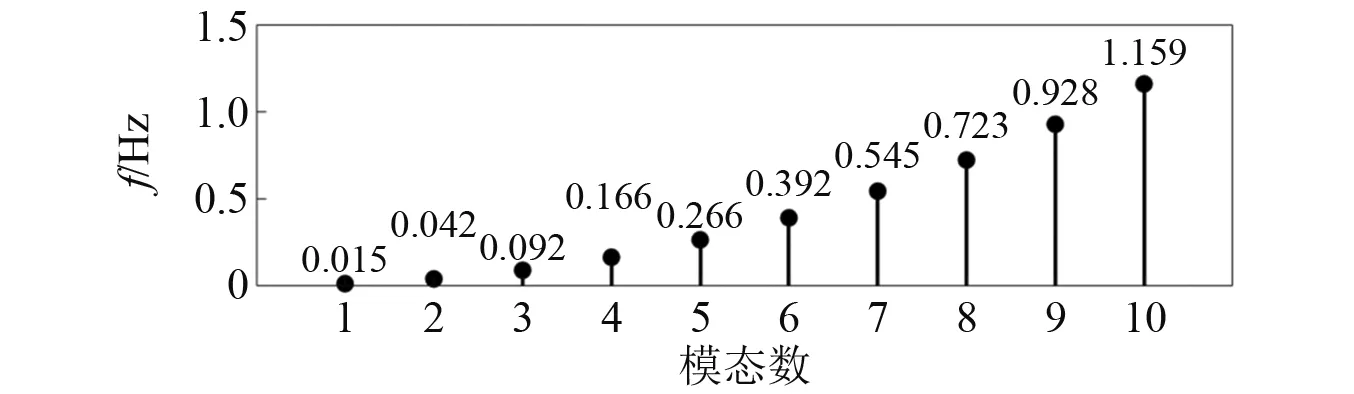
图12 立管固有频率Fig.12 Natural frequency of the riser

图13 立管各阶模态振型Fig.13 Mode shapes of the riser
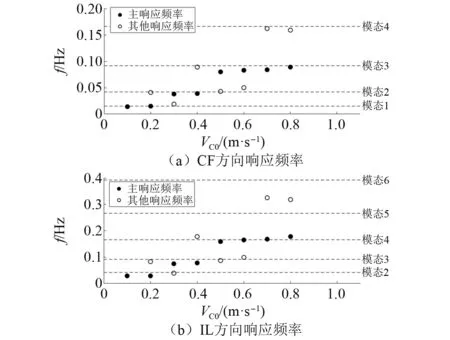
图14 立管涡激振动响应频率Fig.14 The response frequencies of the riser
图15为立管在0.2 m/s, 0.4 m/s, 0.6 m/s, 0.8 m/s共4种表层流速下,全年的立管涡激振动疲劳损伤在管长方向与截面位置上的分布情况。随着流速的增加,立管涡激振动激发模态会随之改变,这将导致疲劳损伤沿立管长度方向的分布发生变化。同时,虽然立管在CF方向上的涡激振动响应幅值一般大于IL方向上的涡激振动响应,但是IL方向上的响应频率是CF方向上的2倍,而疲劳损伤是振动频率和幅值共同作用的结果,高频小幅振动与低频大幅振动,可能带来相同的疲劳损伤,图 15(d)中立管的最大涡激振动疲劳损伤出现在IL方向上也因此得以解释。
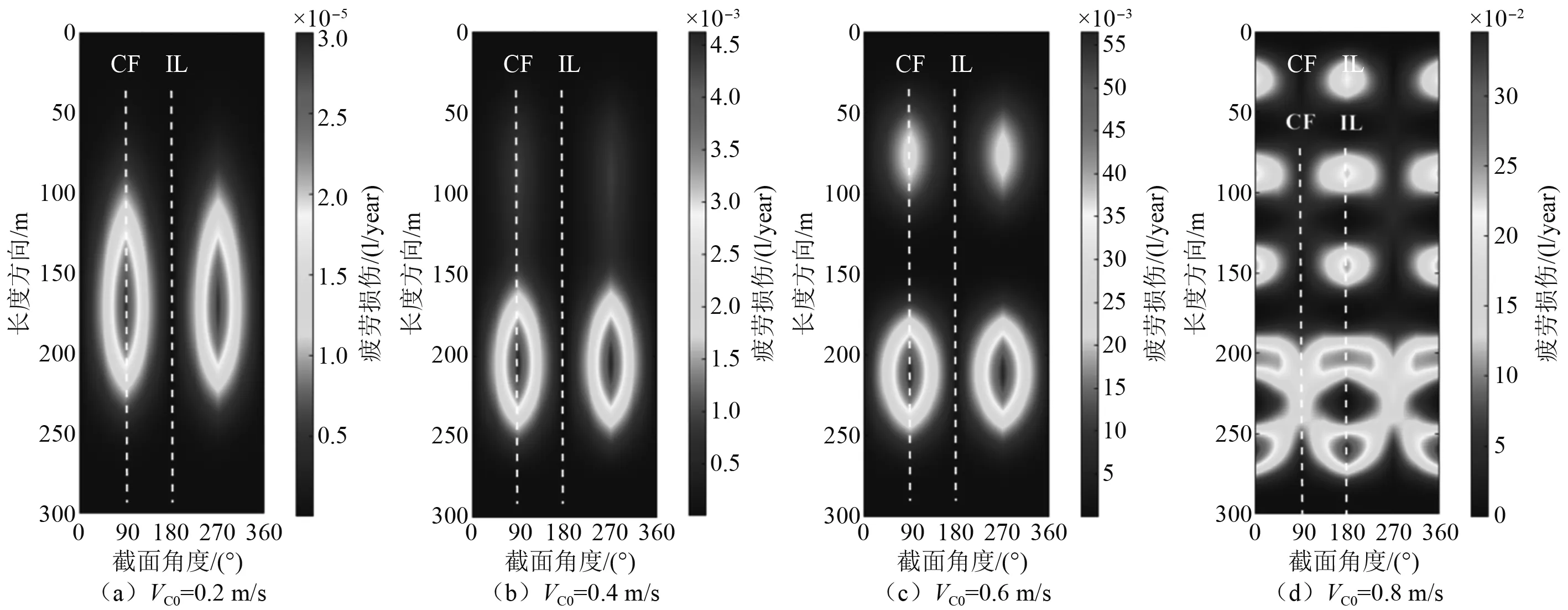
图15 立管涡激振动疲劳损伤分布Fig.15 VIV-induced fatigue damage distribution
在分析的8种表层流速下,立管沿管长方向的最大涡激振动疲劳损伤分布如图16所示,可以发现,其最大疲劳损伤并非完全按照立管的某一阶模态振型分布。这是因为立管CF与IL方向上立涡激振动的主导模态不同,导致CF与IL方向上疲劳损伤积累的分布不同。当分析长度方向上立管的最大涡激振动疲劳损伤时,此最大值可能出现在CF或IL方向上,故沿管长的分布并不完全与立管的某阶模态振型吻合。
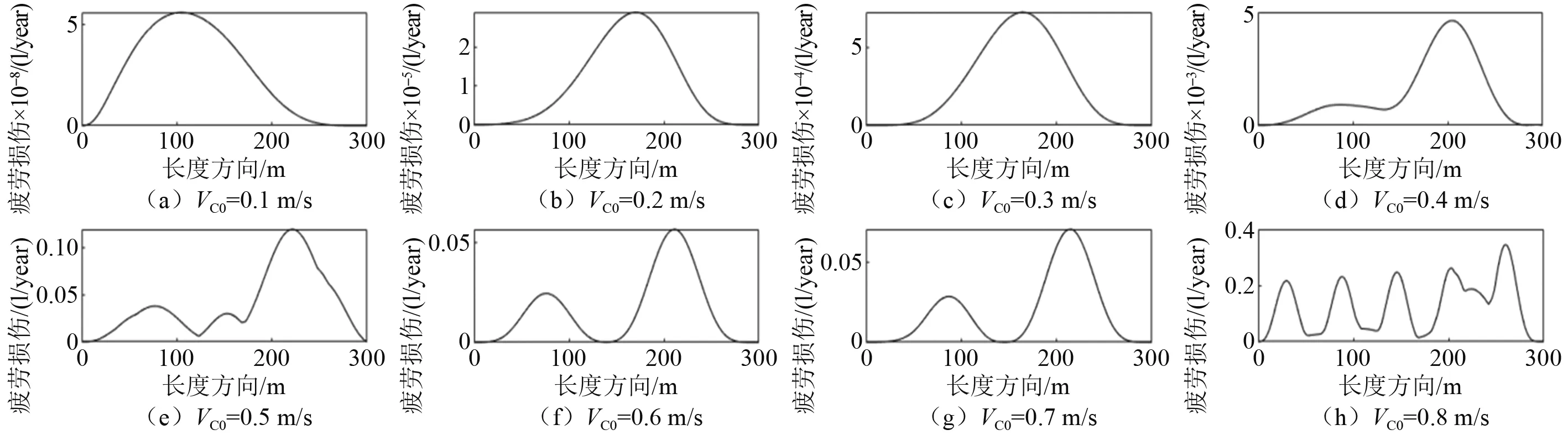
图16 立管截面最大涡激振动疲劳损伤沿管长分布曲线Fig.16 The most serious VIV-induced fatigue damage on the cross sections along the riser
3.3 疲劳结果分析对比
将立管在各个海况下的全年疲劳损伤与涡激振动损伤乘以相应海况出现概率并求和后可得到立管的全年总的波致疲劳损伤与涡激振动损伤情况。
如图17所示,对比立管波致疲劳损伤与涡激振动损伤的分布情况,可以发现:波致疲劳损伤主要积累在立管接近平台处,而涡激振动疲劳损伤与之相反,其主要集中在立管接近自由端的部分;波致疲劳损伤几乎完全分布在立管的IL方向上,而涡激振动疲劳损伤则主要分布于立管的CF方向上。
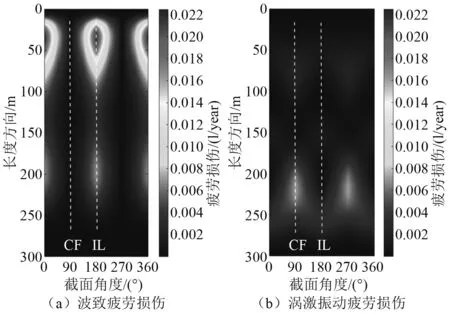
图17 立管全年疲劳损伤分布Fig.17 The fatigue damage distribution of the riser in one year
图 13(a)所示为全年总的波致疲劳与涡激振动疲劳最大值沿管长的分布,最大波致疲劳损伤值约为最大涡激振动疲劳损伤值的4倍。但是,相比于立管波致运动的预报,立管流致涡激振动响应预报存在更大的不确定性因素。因此,在进行立管涡激振动疲劳分析时,需乘以极大的安全系数来保证计算结果的安全性。依据DNV的推荐做法[19],对于常见形式钢质立管的波致疲劳损伤安全系数一般选取3,而涡激振动疲劳损伤推荐采用更高级别的安全系数,一般选取10~15。本文分别将图18(a)中波致疲劳和流致涡激振动诱导疲劳结果乘以了对应的安全系数,重新对比情况如图18(b)所示。可以看出,在取水管疲劳强度评估和安全设计中,两种疲劳损伤的严重程度较为接近。
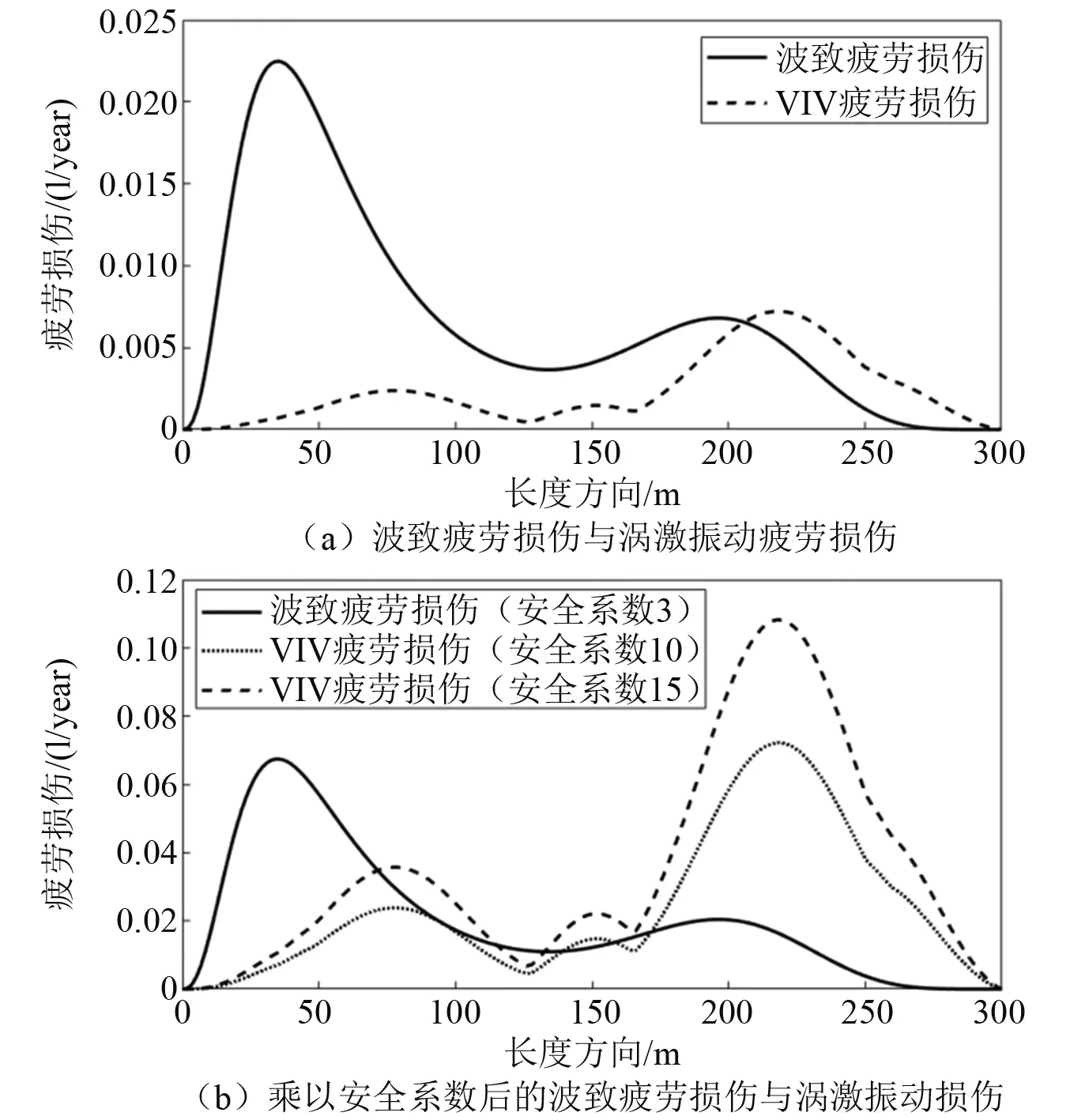
图18 立管管长方向最大全年疲劳损伤分布Fig.18 The most serious fatigue damage distribution along the length in one year
4 结 论
为了研究悬垂立管的波致疲劳与涡激振动疲劳特点,本文基于Miner线性疲劳累积损伤理论,计算得到了悬垂立管全年的疲劳损伤情况,主要得出以下结论:
(1)悬垂立管的波致疲劳损伤分布主要受海浪谱的周期参数影响,而海浪谱的波高参数主要影响疲劳损伤的积累速度。
(2)悬垂立管截面上涡激振动疲劳损伤最大位置需根据具体海况进行计算,受激发频率与幅值的同时影响,CF和IL方向上的疲劳损伤情况并不保持某一方绝对主导。
(3)按出现概率考虑所有海况的作用影响后,悬垂立管的全年波致疲劳损伤主要积累在立管与平台连接处附近、与浪流方向相同的截面位置上;全年涡激振动疲劳损伤主要积累在立管底部自由端附近、与浪流方向垂直的截面位置上。
(4)波致疲劳和涡激振动诱导疲劳的安全系数分别取3和15之后,两者导致的疲劳损伤程度在一个数量级上,后者相对更为严重。
