基于CFD-DEM耦合的埋地输气管道泄漏声场分析

王 强, 薛 生,2, 郑晓亮, 张 磊, 谢晓贤

(1. 安徽理工大学 安全科学与工程学院,安徽 淮南 232001;2. 安徽理工大学 煤炭安全精准开采国家地方联合工程研究中心,安徽 淮南 232001; 3. 安徽理工大学 电气与信息工程学院,安徽 淮南 232001)

输气管道泄漏导致环境污染、自然资源浪费,甚至引起严重的公共安全事故。因此,管道泄漏检测对于预防事故风险具有重要意义。目前,基于声波的检测方法是综合性能最优的管道泄漏检测方式[1-3]。(分析泄漏声波的产生机理以及声场特征,可以为泄漏声波检测提供理论依据和参数支持。

现有研究主要集中在对架空管道声波产生机理的理论建模与试验测试。刘翠伟等[4-5]使用计算流体力学(computational fluid dynamic, CFD)方法分析泄漏流场压力波动,并结合声类比方法(FW-H方程[6-7])研究了泄漏引起的气动噪声产生机理。泄漏声源由偶极子和四极子声源叠加产生,偶极子和四极子声源分别由湍流脉动和气固作用产生。Mostafapour等[8]则从管壁应力波的角度研究泄漏声发射现象,认为高压管道泄漏引起的局部能量损失会产生应力波,该应力波沿管壁传播并且可使用声波或加速度传感器进行检测。该研究利用Donnell圆柱壳非线性理论推导并求解了简支边界条件下的管壁运动方程,在试验条件下测试了持续泄漏的声发射信号,由理论分析和试验测试获得的信号频谱具有较好的一致性。

对于埋地管道,Mostafapour等[9]也分析了外部土壤对管壁非线性振动的影响。在Donnell圆柱壳非线性理论的基础上,将土壤视为各向同性均匀介质,使用势函数分析周围介质对管壁径向位移的影响,结合Weaver-Unny模型进行气固作用分析。使用Galerkin方法求解上述模型,得到了埋地管道泄漏引起的管壁径向位移。Ebrahimi-Moghadam等[10]研究了管道泄漏的数值分析方法,用以估计埋地管道的泄漏量。使用稳态可压缩湍流进行泄漏建模,将土壤视为多孔介质,推导了土壤黏性阻力和惯性阻力作用下的流体控制方程,数值分析结果表明土壤多孔介质阻隔导致泄漏气体衰减为亚音速流。然而,该研究忽略了泄漏气体与土壤的相互作用,缺少对声场特性的分析。

埋地管道泄漏引起的振动声波可沿土壤介质传播。Biot多孔介质波传播理论预测了土介质中3种波的存在,包括两种压缩波和一种剪切波。土介质波传播特性的理论分析和试验结果表明,衰减较慢的P1波和S波是土介质波的主要成分[11-12]。P1波和S波主要传播载体均为土壤固体框架,可采用对固体振动敏感的传感器(地震检波器、加速度传感器等)耦合至土壤表面进行检测[13]。例如,Muggleton等[14]使用管壁周围的分布式光纤声学传感器和土表的地震检波器,实现了泄漏振动声波检测。

综上所述,现有研究缺乏对埋地管道泄漏引起的气动噪声分析,且试验方法局限于单一传感器通道的信号波形、频谱分析或多个通道的相关性分析,无法获取声场分布特征。本文采用计算流体力学与离散元法(computational fluid dynamic and discrete element method,CFD-DEM)耦合分析泄漏气体与土壤颗粒的相互作用,再结合宽频噪声源模型分析泄漏引起的气动噪声分布特征。针对埋地管道泄漏声场测试问题,引入阵列技术进行泄漏声场成像。所提出基于CFD-DEM耦合分析的埋地管道泄漏声场分析方法能够获取流固耦合作用下的声场产生机理和分布特征,泄漏声场的阵列成像可进一步验证理论模型的准确性。

1 管道泄漏CFD-DEM耦合分析

本文采用CFD-DEM耦合分析方法来描述泄漏流体与泄漏孔附近土壤的相互作用,流体在管内以及管外土壤区域的流动使用流体控制方程进行描述,将土壤视为离散的土壤颗粒并使用颗粒运动方程描述。管道泄漏流固耦合分析模型分为3个部分:流体控制方程;颗粒运动方程;CFD-DEM耦合算法。

1.1 流体控制方程

埋地输气管道泄漏流体的控制方程[15]如下。

质量守恒方程(连续性方程)为

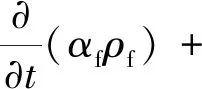
(1)

动量守恒方程为

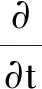
(2)

式中:αf为流体的体积分数;ρf为流体密度;uf为流体速度矢量;pf为流体压力;g为重力加速度;Tf为流体应力张量;Sf为流体与颗粒动量交换力源项;体积分数αf为流体单元中流体所占体积份额[16];源项Sf则为流体与颗粒相互作用产生的动量源项[17]。在流固作用过程中,流体体积分数αf和动量交换力源项Sf均会因颗粒运动而发生变化。

泄漏流体在管道内压的作用下具有高雷诺数,需进行湍流建模。Realizablek-ε模型适用于射流、管内流动以及边界层流动等多种流动,因此,本文选取Realizablek-ε模型进行管道泄漏湍流建模[18]。

1.2 颗粒运动方程

对于流体单元内的颗粒,其运动由平移和旋转组成,根据牛顿第二定律可得颗粒运动方程[19]为

(3)

(4)

式中:mp和up分别为颗粒质量和速度矢量;ωp为颗粒角速度矢量;Fc,n和Fc,t分别为颗粒-颗粒、颗粒-壁面碰撞产生的法向和切向接触力;Fa为附着力;Ff为流体对颗粒的作用力;Ip为颗粒的惯性矩;Mc为切向接触力引起的力矩;Mf为流体速度梯度引起的力矩;Mr为滚阻力矩。图1为泄漏流体作用下土壤颗粒的受力分析示意图,各个变量将在下文解释。

图1 颗粒受力分析Fig.1 Force of particle

1.2.1 流体与颗粒的作用力

流体对颗粒的作用力一般分为曳力Fd和非曳力Fn-d,即Ff=Fd+Fn-d。在颗粒直径较小的情况下,非曳力可忽略,曳力在流体作用力中起主导作用。曳力计算公式为

(5)

式中,Dp为颗粒直径,曳力系数Cd取决于颗粒浓度和颗粒雷诺数。Gidaspow模型[20]能够覆盖完整的颗粒浓度范围,本文选取该模型计算曳力系数Cd。

1.2.2 颗粒间的作用力

颗粒-颗粒、颗粒-壁面碰撞采用Hertz-Mindlin接触模型进行描述[21]。法向接触力Fc,n包含弹性力Fe和黏滞力Fv两部分,即Fc,n=Fe+Fv。弹性力Fe和黏滞力Fv的定义[22]为

(6)

(7)

切向接触力Fc,t的定义[23]为

(8)

Hertz-Mindlin接触模型不包含附着力,因此引入JKR(Johnson-Kendall-Roberts)接触模型以分析附着力对颗粒接触的影响。基于JKR模型的附着力表达式[24]为

(9)

式中:γ为表面能量;a为接触面半径。

1.2.3 力 矩

切向接触力矩Mc定义为

(10)

式中,n为法向方向向量。

对于流体速度梯度引起的力矩Mf,其计算方法为

(11)

式中:ωf为颗粒所在位置的流体角速度矢量;系数CR根据颗粒雷诺数ReΩ(基于颗粒旋转速度)计算得到。

滚阻力矩Mr的表达式为

(12)

式中:μr为滚阻系数;rp为颗粒滚动半径。

1.3 CFD-DEM耦合

由1.1节流体控制方程和1.2节颗粒运动方程的分析可知,通过改变流体体积分数αf和动量交换力源项Sf的形式以施加颗粒对流体的影响;流体对颗粒运动的影响则以作用力Ff和力矩Mf的形式体现。图2为CFD-DEM耦合算法流程,tf和tp分别为CFD和DEM时间。CFD计算过程中,通过DEM计算结果更新颗粒体积分数αp、流体作用力Ff以及颗粒位置,从而计算流体体积分数αf、动量交换力源项Sf并求解流体控制方程组。DEM计算过程中,通过CFD计算结果更新流体体积分数αf、流体速度uf、角速度ωf、流体密度ρf和黏度μf,从而计算流体作用力Ff和力矩Mf,并求解颗粒运动方程。通过上述过程,耦合算法可实现CFD和DEM的数据交换。

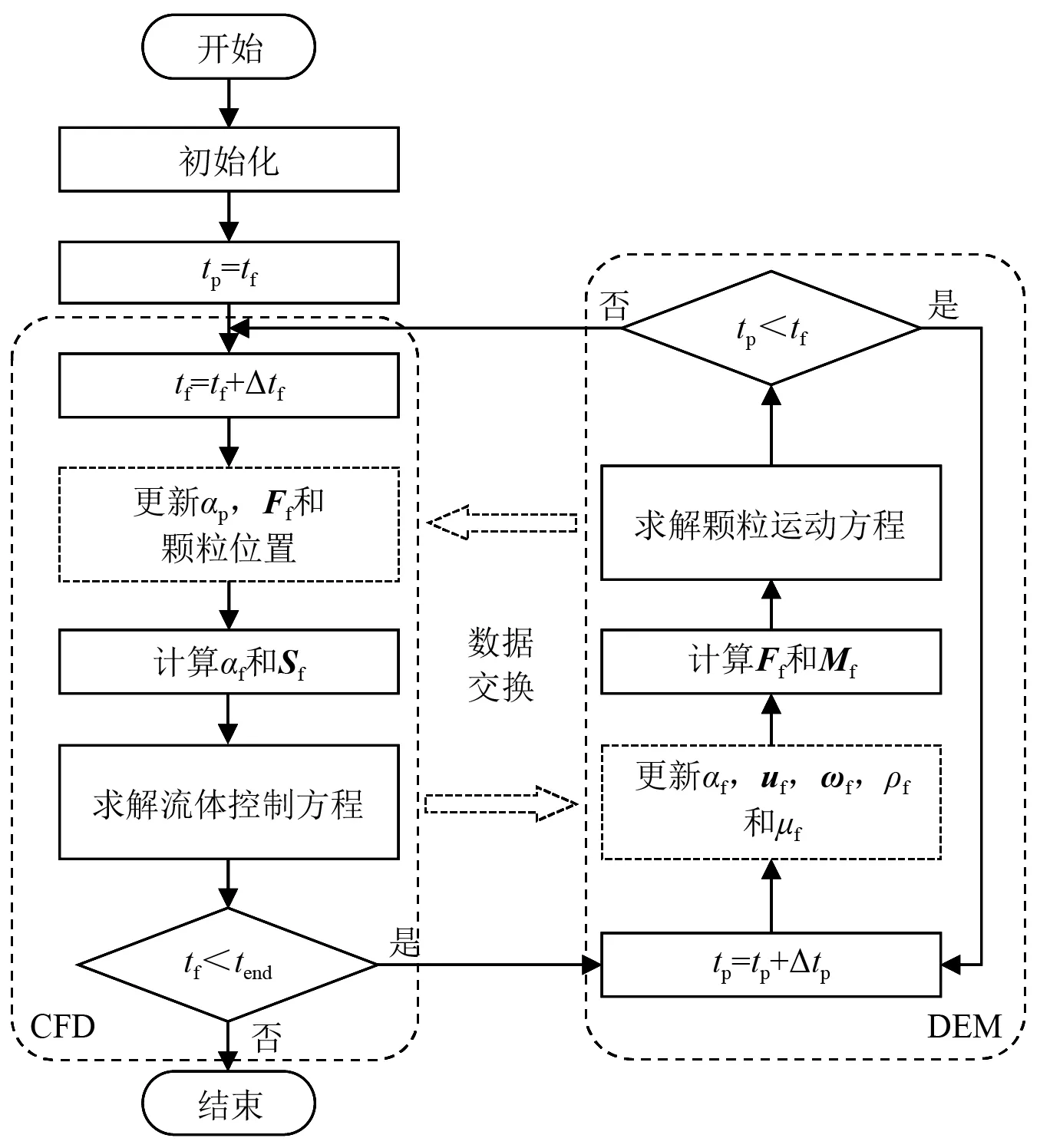
图2 CFD-DEM耦合算法流程Fig.2 Flow chart of coupled CFD-DEM algorithm

2 管道泄漏声场分析

2.1 宽频噪声源模型

宽频噪声源模型[25]无需流体控制方程的瞬态解,只需使用RANS方程计算湍流统计量(如基于RANS方程得到的平均速度、湍流动能k和湍流耗散率ε等),再结合半经验关系式以及Lighthill声类比方法即可获取噪声源分布,实际应用中不受自由场条件约束。因此,宽频噪声源模型适用于埋地管道工况下的非自由场湍流噪声计算,可获取声源位置,实现泄漏声场分布特征分析。对于埋地管道泄漏喷流,可采用喷流噪声源模型计算各向异性喷流噪声,采用边界层噪声源模型计算固体(管壁、土壤)表面的湍流噪声。

2.1.1 喷流噪声源模型

针对轴对称射流中湍流的各向异性,Goldstein对Ribner模型[26]进行改进,得到了轴对称射流噪声源模型。在Goldstein的模型[27]中,单位体积内湍流射流产生的总声功率为

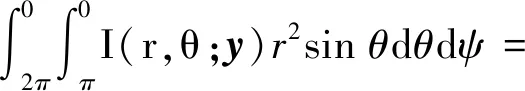
(13)

式中:r和θ为接收器位置的径向和角坐标;I(r,θ;y)为单位体积内射流的定向声强。

2.1.2 边界层噪声源模型

对于固体表面的湍流边界层流动,基于声类比的Curle积分可近似度量局部固体表面对总声功率的贡献。根据Curle积分推导可得

(14)

式中:τ为激发时间(τ=t-r/a0);S为积分面。根据式(14),声强可近似表达为

(15)

式中:Ac为相关面积;r≡|x-y|;θ为|x-y|与壁面法线方向n的夹角。由整个固体表面产生的总声功率可通过式(16)计算

(16)

式中,I(y)为单位面积固体表面所产生的声强。

2.2 声场成像

均匀圆形阵列(uniform circular array, UCA)是一种典型的平面阵列,相较于其他阵列,其对不同方向的响应具有更好的一致性,可以准确反应不同方向或位置的信号源能量分布。本文研究对象为埋地管道的泄漏声场分布,在土壤空间中,泄漏引起的振动声波沿土壤介质向外传播。因此,将UCA布置于土壤表面进行信号采集,使用相应算法即可实现土壤空间中的泄漏振动声源成像。Biot多孔介质波传播理论预测了土介质中3种波的存在,土介质波传播特性的理论分析和试验结果表明,沿固体框架传播的P1波和S波占据主导,因此信号建模需考虑两种波的影响。

仅考虑单个泄漏源,得到P1波和S波混合信号矩阵为

X(t)=AS(t)+N(t)=

式中:阵列流形矩阵A由P1波和S波的延时向量aP1(x,y,z)和aS(x,y,z)构成,参考传感器接收信号S(t)由P1波和S波分量sP1(t)和sS(t)构成;N(t)为噪声信号矩阵。对于M元UCA,两种波从聚焦点到达阵列的延时向量表达式为

(18)

式中:rm(m=1, 2, …,M)为聚焦点到传感器m的距离;聚焦点坐标为(x,y,z),传感器m的坐标为(xm,ym,zm),则rm=[(xm-x)2+(ym-y)2+(zm-z)2]1/2;cwave为波速;下标“wave=P1, S”分别对应P1波和S波。

相较于子空间分解类DOA估计算法,Capon算法直接使用延时向量进行信号协方差矩阵加权,能够更好的反应信源能量分布[28-30]。将坐标(x,y,z)作为变量,得到基于Capon算法的三维空间谱函数

(19)

式中,阵列信号协方差矩阵R=E[X(t)XH(t)]。通过改变聚焦点位置(x,y,z)进行空间谱搜索,可获取土壤空间中泄漏振动声源的能量分布,即振动声源成像。

3 数值分析

3.1 数值模型

为分析管道泄漏造成的气体与土壤流固耦合作用,建立如图3所示的数值分析模型。埋地管道内径为100 mm,长度为1 000 mm。管道两端分别设置为压力入口和压力出口,位于管道中部且开口垂直向上的泄漏孔直径为2 mm,泄漏孔埋深为1 000 mm。管内流体经过泄漏孔进入土壤区域,因此设置土壤区域的上表面为第二个压力出口。本文关注流固耦合作用下的泄漏流场及其产生的声场,因此将泄漏流体简化为空气,将土壤介质简化为圆形颗粒,土壤颗粒由直径3 mm和1 mm的两种颗粒混合而成。忽略2 mm直径微小泄漏对管道内压的影响,将管道两端的入口压力和出口压力设置为恒定的1 MPa,即管道内压为1 MPa。

图3 数值分析模型(mm)Fig.3 Model of numerical analysis(mm)

3.2 颗粒运动分析

图4为不同时刻的土壤颗粒速度分布云图,泄漏孔位于颗粒底部中央位置。本文关注泄漏形成后的持续稳定流场和声场,因此选取1～3 s时间窗口进行分析,此时流固耦合已达到稳定。由图4可知,泄漏孔上方空洞的大小和形状随时间的推移基本保持稳定。空洞内颗粒运动速度达10 m/s,空洞外部颗粒保持静止状态。

图4 土壤颗粒速度Fig.4 Speeds of soil particles

泄漏孔位于空洞下方,且开口向上,可以判断空洞由泄漏喷流造成。由此可知,将土壤简化为多孔介质的分析方法忽略了泄漏喷流对土壤的冲击作用。空洞内的流体流动不受多孔介质的阻碍,湍流动能损失更小,更有利于产生气动噪声。另一方面,外部土壤保持静止,说明仿真工况下的气体泄漏无法从地面直接察觉,泄漏隐蔽性较强。

3.3 流场分析

通过对比架空管道与埋地管道的泄漏流场特性,分析土壤颗粒对泄漏喷流的阻碍作用。图5为架空管道泄漏流场分布,图5(a)为速度场,图5(b)为压力场,图5(c)为湍流动能。由图5可知:1 MPa内压的架空管道泄漏气体在泄漏孔区域达到最大流速(1 310 m/s),高流速(>1 000 m/s)区域呈尖锥形;泄漏孔区域的流体压力迅速由1 MPa下降为0.5 MPa,且泄漏孔下边缘处出现了低压区;湍流动能集中分布在泄漏孔壁面附近。

图5 架空管道泄漏流场Fig.5 Fluid field for overhead pipe leak

图6为埋地管道泄漏流场分布,图6(a)～图6(c)分别对应速度场、压力场和湍流动能。对比图6(a)和图5(a)可知,土壤的阻碍作用导致埋地管道泄漏流速峰值低于架空管道。随着泄漏流体进入土壤颗粒区域,图4所示空洞区域内的流体维持较高流速(>700 m/s),而架空管道在该区域的流速低于600 m/s。由于土壤颗粒极大限制了外部流体的体积分数,埋地管道外部流场静压高于架空管道,且在空洞区域出现了压力积聚,出现了如图6(b)所示的管道内外压力降缓冲区。图6(c)所示泄漏孔壁附近的湍流动能相较于图5(c)有所下降,峰值由7.1×104m2/s2下降至1.4×104m2/s2。

图6 埋地管道泄漏流场Fig.6 Fluid field for buried pipe leak

区别于架空管道,图4所示不同时刻的土壤空洞轮廓以及内部颗粒运动状态具有随机性,需要考虑土壤颗粒的随机运动以及流固耦合对埋地管道流场分布特征的影响。图7为埋地管道泄漏流体速度分布,不同时刻的最大流速以及速度场分布特征有所变化,但整体上高速喷流均保持集中在土壤空洞和泄漏孔内部。土壤空洞与泄漏高速喷流伴随产生,证明了空洞是由泄漏喷流造成,空洞内部的流体与颗粒相互作用,造成了两种介质的运动特性变化。

图7 不同时刻埋地管道泄漏流体速度Fig.7 Speeds of fluid for buried pipe leak in different time

3.4 声场分析

基于流场特性,使用宽频噪声源模型分析泄漏声场。图8(a)和图8(b)分别为架空管道和埋地管道的泄漏声场分布。可知,架空管道泄漏声场分布范围较大,除泄漏孔附近,泄漏孔上方长条形区域也分布有20～50 dB的声场。与流体的速度场和湍流动能一样,埋地管道泄漏声场能量也有所降低,且声场区域与图6(a)以及图7所示高速喷流区域保持一致,被限制在土壤空洞和泄漏孔内。对比图6(a)和图8(b)可知,埋地管道的泄漏喷流速度超过了声速,由湍流脉动产生的四极子声源占据主导,因此四极子声源和高速喷流区域重合。

图8 管道泄漏声场Fig.8 Acoustic field for pipe leak

图9为不同时刻的埋地管道泄漏声场分布,对比图7可知,声场的最大声压级与流体速度的关联性较强,流体速度快则声压级大。对1～3 s的流场和声场每隔0.1 s抽取最大值和平均值,计算出二者最大值和平均值的相关系数分别为0.82和0.75,说明流场和声场具有强相关性。这一结果进一步验证了埋地管道泄漏声场由湍流脉动产生。

图9 不同时刻埋地管道泄漏声场Fig.9 Acoustic field for buried pipe leak in different time

由上述颗粒运动、流场以及声场的数值分析结果可知,埋地管道泄漏喷流的冲击作用使泄漏孔区域的土壤形成了空洞,外部土壤则依然保持稳定,泄漏隐蔽性强。空洞和泄漏孔内的流体流速超过声速,为气动噪声的产生创造了条件。但相较于架空管道,土壤的阻碍作用导致流体流速减慢、湍流动能减弱,空洞内形成流体压力降缓冲区,空洞内的颗粒运动速度加快,能量由流体传递至土壤。泄漏孔和空洞内高速流动的流体产生了气动噪声,气动声源与高速喷流区域重合,二者关联性较强。由于高速喷流被限制在空洞和泄漏孔内,因此埋地管道泄漏声源也处于空洞和泄漏内,声源位置即泄漏位置。

3.5 泄漏孔朝向的影响

考虑实际工况下泄漏孔位置具有随机性,除泄漏孔朝上,增设泄漏孔朝向管道侧面和底部两种工况,分析泄漏孔朝向对土壤颗粒运动、流场以及声场的影响。图10为管道上方、侧面以及底部泄漏孔示意图。为方便分析泄漏孔朝向的影响,选取管道轴向横截面进行参数分布特征分析。

图10 泄漏孔朝向示意图Fig.10 Illustration of direction of leak hole

图11为不同泄漏孔朝向的土壤颗粒速度分布云图,圆形空白区域为管道横截面。对于不同朝向的泄漏孔,泄漏孔附近均出现了土壤空洞,且空洞形状与泄漏喷流的方向相关。然而,图11所示由管道上方泄漏孔形成的空洞横截面最大,而管道侧面和底部泄漏孔形成的空洞横截面则较小。分析原因为:当泄漏孔向上,泄漏喷流对土壤的作用力抵消了重力和外围土壤的作用力,形成了较大的空洞;当泄漏孔位于侧面或底部,泄漏喷流对土壤的作用力方向主要朝向侧面或底部,空洞外围土壤则在重力的作用下重新回落到空洞内部,致使空洞减小。因此,方向向上的管道泄漏更容易改变泄漏孔区域的土壤结构。

图11 不同泄漏孔朝向的土壤颗粒速度Fig.11 Speeds of soil particles with multiple leak hole directions

图12为不同泄漏孔朝向的流场和声场分布。相较于上方泄漏孔工况,侧面和底部泄漏孔形成的喷流速度更加缓慢、湍流动能更弱,对应声场的最大声压级也更低。这一结果与土壤颗粒运动分析基本一致,重力作用导致土壤回落至侧面或底部空洞,从而阻碍了流场发展并削弱了声场能量。

图12 不同泄漏孔朝向的流场和声场Fig.12 Fluid and acoustic fields with multiple leak hole directions

4 声场测试

4.1 试验设置

图13为埋地管道泄漏振动声波检测试验平台,该试验平台由供气装置、埋地管道以及数据采集设备组成。供气装置包含空压机、储气罐、减压阀以及球阀若干。埋地泄漏管道由预留直径2 mm圆形泄漏孔的DN100镀锌钢管构成。数据采集设备包含加速度传感器、采集仪和计算机。对于埋地管道,泄漏引起的振动声波以P1波和S波形式沿土壤固体框架传播至地面,需采用对固体振动较为敏感的传感器进行信号采集。因此,本文使用加速度传感器耦合至地面进行泄漏振动声波测试。INV9828型加速度传感器灵敏度为500 mV/g,频响范围为0.2 Hz～2.5 kHz,输出信号为加速度(单位m/s2)。INV3062C型采集仪支持8通道216 kHz采样率同步采集,8枚加速度传感器构成8元UCA阵列。计算机CPU型号为i7 12700H,配备16 GB RAM。

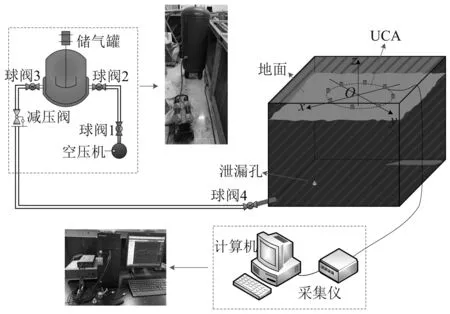
图13 试验平台Fig.13 Test rig

通过改变阵列位置来改变泄漏源与阵列的相对位置关系,从而实现对不同位置的泄漏振动声源成像。见图13,以UCA阵列几何中心作为原点构建参考系,设置3个泄漏位置坐标为(0.5 m, 0.3 m, -0.5 m),(0.5 m, 0.2 m, -0.7 m),(0.5 m, 0, -0.9 m)。试验前使用空压机为储气罐加压至1.1 MPa,再使用储气罐出口减压阀调节管道内压为1.0 MPa并保持稳定。试验过程中关闭空压机以防止噪声干扰,且试验环境下无其他噪声干扰源。待泄漏稳定后进行信号采集,土介质波的频率一般低于1 kHz,设置采样率为10 kHz以防止波形信息丢失。

4.2 振动声波分析

利用2.2节的三维空间谱进行泄漏振动声源成像,需满足近场判据r<2D2/λ,其中:r为声源到阵列中心的距离;D为阵列孔径;λ为信号波长。因此本节将分析信号波形、频谱以确定波长,从而计算满足近场判据所需的阵列孔径。

图14为地面加速度传感器信号波形和频谱,表明泄漏引起的振动声波信号为连续随机信号,且能量集中在200～600 Hz频段,频响峰值出现在440 Hz。测定图13试验平台所使用回填土的含水饱和度为0.15,孔隙度为0.5,查询丁卫等的研究可得P1波和S波的理论波速分别为1 127 m/s和135 m/s。可计算出试验条件下P1波和S波的波长分别为2.56 m和0.31 m。泄漏源与阵列的最大距离为1.03 m,结合P1波波长2.56 m,得出满足近场判据的最小孔径为1.15 m,因此设置UCA孔径为1.2 m。

图14 信号波形、频谱Fig.14 Waveform and spectrum of signal

4.3 声场成像

根据2.2节基于Capon空间谱的声场成像原理,分别将P1波和S波波速代入式(19)进行声场成像。图15为使用P1波波速cP1的声场成像(yz面和xy面),图15(a)～图15(c)对应3个泄漏位置。图15中dB为以空间谱PCapon的最大值为参考,归一化得到的空间谱功率级,与3.4节的声压级为不同物理量。由于泄漏振动声波通过土壤传播,传播过程存在衰减,加速度传感器检测到的信号为衰减后的振动信号。且空间谱输出功率为8个传感器信号的加权叠加,因此基于阵列的声场成像只能反应泄漏振动声源的能量分布,无法得出真实的声压级。由图15可知,不同位置的声场成像在泄漏位置均产生了较强的能量反应,说明声场能量集中在泄漏位置,与仿真分析结果相符。除泄漏位置,其他位置也出现了较高的能量响应,分析原为试验箱体反射声波造成了混响干扰。

图15 使用cP1的声场成像Fig.15 Acoustic field imaging using cP1

图16为使用S波波速cS的声场成像(yz面和xy面),图16(a)～图16(c)对应3个泄漏位置,dB的意义参考图15。区别于图15,图16所示使用S波波速的声场成像在泄漏位置的能量响应减弱,在其他区域出现了较多周期性的响应。分析原因为P1波和S波的混合干扰造成。当使用P1波波速cP1进行成像时,对S波分量的处理则相当于将S波延时向量aS(x,y,z)中的cS替换为cP1。由于cP1>cS,由式(18)可知,此时难以通过调整聚焦位置(x,y,z)来改变S波相位,无法实现S波分量的空间谱搜索。因此,使用cP1进行成像时,可忽略S波分量的干扰。反之,使用S波波速cS进行成像时,将P1波延时向量aP1(x,y,z)中的cP1替换为cS,则P1波分量的空间谱将出现周期性重复,形成干扰。综上所示,使用P1波波速进行空间谱成像更有利反应泄漏振动声源的能量分布。

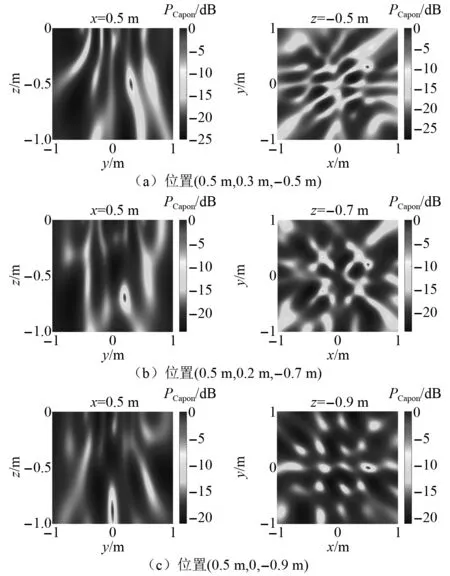
图16 使用cS的声场成像Fig.16 Acoustic field imaging using cS

4.4 泄漏孔朝向的影响

通过旋转图13所示管道使泄漏孔朝向侧面和底部,进行不同泄漏孔朝向的声场成像分析。图17为不同泄漏孔朝向的P1波声场成像,图中标记了管道横截面以及泄漏孔的位置和朝向,上方泄漏孔的位置为(0.5 m, 0.3 m, -0.5 m),侧面泄漏孔的位置为(0.50 m, 0.35 m, -0.55 m),底部泄漏孔的位置为(0.5 m, 0.3 m, -0.6 m)。由图17可知,不同泄漏孔朝向的声场成像均在泄漏位置形成了突出的响应。然而,底部泄漏孔的声场成像相对更加分散,无法准确指示泄漏位置。分析原因为,UCA阵列位于地面,管道底部泄漏引起的振动声波需经过管道才能传播至地面。土壤与管道的声阻抗特性差异较大,声波的反射或散射现象改变了泄漏振动声波的传播路径,从而影响了底部泄漏孔的声场成像。

图17 不同泄漏孔朝向的P1波声场成像Fig.17 Acoustic field imaging using P1 wave with multiple leak hole directions

上述结果表明,可使用UCA阵列进行泄漏声场成像,从而指示出泄漏孔的位置。但底部泄漏孔受管道结构的影响,泄漏声场成像准确度有所降低。

5 结 论

为研究埋地管道泄漏流固耦合作用过程,明确泄漏声场产生机理,采用CFD-DEM耦合方法分析泄漏喷流与土壤颗粒的相互作用,结合宽频噪声源模型和声场成像技术实现了泄漏振动声源的仿真分析和试验测试。基于1 MPa管道内压工况,得出以下主要结论:

(1)泄漏喷流冲击使土壤形成空洞,空洞内部土壤颗粒运动速度达到10 m/s,外部土壤则保持稳定,增加了泄漏隐蔽性;相较于架空管道,土壤阻碍导致埋地管道流体流速减慢、湍流动能减弱,空洞内压力积聚,形成压力降缓冲区,能量由流体传递至土壤;相较于侧面和底部泄漏孔,上方泄漏孔产生的土壤空洞更大,流场和声场能量更强。

(2)泄漏孔和空洞内的高速喷流产生了气动噪声,声源位置与高速喷流区域重合,但最大声压级相较于架空管道降低20～40 dB(图8、图9);泄漏孔和空洞内的泄漏流场流速峰值达到了1 000 m/s,且流速和声压级的最大值和平均值相关系数分别为0.82和0.75,二者相关性强,说明由高速喷流的湍流脉动所形成的四极子声源在泄漏声源中占据主导。

(3)试验结果表明,基于加速度传感器阵列的声场成像技术能够反应泄漏声场能量分布,声场成像在泄漏位置产生了较强的响应,与数值分析结果相符。基于P1波波速的声场成像更加纯净,使用S波波速进行成像时则存在P1波干扰问题。利用阵列技术进行泄漏检测具有可行性,将P1波波速作为空间谱函数的参数更加有利于精确成像从而实现定位。同时,管道底部泄漏孔所产生的信号易受管道结构干扰,工程应用中应考虑相应的规避措施,如改变阵列位置使信号传播路径避开管道结构。