新型结构的四旋翼无人机视觉导航半物理仿真平台设计及试验

黄峰, 王威雄, 林忠麟, 吴衔誉, 庄嘉权

(福州大学 机械工程及自动化学院, 福建 福州 350108)

0 引言

20世纪以来,四旋翼无人机由于低成本、高机动、小体积等特点,被越来越频繁地应用在各种军事任务中,例如战场侦察、精准打击以及空地协同等[1-4]。在复杂多变的战场环境下,高精度导航技术尤其重要,其中视觉导航采用的视觉传感器相比于传统惯性导航的惯性测量单元,具有被动式、隐蔽性强、采集信息更加丰富的优点。针对现有视觉导航算法大多精度低、稳定性差的问题,需要在进行视觉导航算法的室外飞行试验前,设计并研制四旋翼无人机视觉导航半物理仿真平台,开展半物理仿真实验验证,在提高算法迭代速度的同时避免由于算法缺陷导致的飞行事故和经济损失。

当前无人机仿真系统主要可分为三类:数字仿真系统、硬件在环仿真系统以及半物理仿真系统[5]。无人机数字仿真系统可通过构建三维模型以及仿真场景,实现无人机飞行的数字仿真。林传健等[6]设计研发了一种无人机跟踪系统仿真平台,采用视景仿真软件进行动画显示,将数学仿真软件作为模型计算工具,还原了实际无人机飞行跟踪的场景。数字仿真在飞行航机规划以及飞行仿真演示等领域也有着广泛运用[7-8]。完全基于计算机的数字仿真系统,虽然能够大幅度降低成本,但是通常忽略了实际无人机系统中各个物理元件间的交互所产生的影响,因此仿真结果通常与实际情况偏差较大。

硬件在环仿真系统是指将需要仿真部分的硬件放入数字仿真回路中进行仿真[9-11]。例如分布式架构KASSANDRA,可以实现不同仿真工具之间的通讯,真实的硬件实体可以与仿真实体无缝衔接,达到更准确的仿真[12]。国内的国防科技大学也研发出了KDRTS/YH_ASTAR/YH-SUPE等,可以支持复杂的硬件在环回路仿真,并可以与数学仿真软件进行通讯[13]。这类仿真系统有着确定性的实时仿真能力以及数据采集能力,结合计算机仿真技术可以更真实地模拟出飞机在不同环境下的飞行状况验证。硬件在环仿真系统中使用计算机模型代替部分传感器或执行机构,与真实传感器存在较大的误差,且这类系统无法提供真实世界的视觉反馈,不适用于无人机视觉导航试验。

半实物仿真系统是指采用仿真设备来模拟试验对象或试验物理环境,并以物理模型、数学模型联合开展仿真实验的系统。半物理仿真可以将飞行系统中无法用数学模型准确描述的部分直接用实物引入。无人机的飞行运动特性模拟也是半实物仿真的重点,常用三轴转台和五轴转台对飞行器的飞行姿态进行模拟。美国研发的S-458R-5Se型红外、激光仿真转台,其模拟转角精度可以达到2″[14]。2018年,韩国延世大学利用动作捕捉相机和两个气动航天模拟器,在光滑的铝表面模拟航天器推力控制,验证自主导航算法试验[15],但是这套系统缺少Z轴运动模拟以及X轴和Y轴的转动。国内哈尔滨工业大学、中国航空工业303所等研究机构也相继研发出了三轴转台、四轴电动转台以及电液控制的五轴转台[15-17]。国内外现有的大型转台由于自由度的限制,大多只能用于实现飞行姿态的模拟,不能对飞行轨迹和飞行场景进行模拟,不适用于无人机视觉导航算法验证。

针对上述问题,本文开展适用于四旋翼无人机视觉导航的半物理仿真平台新型结构设计和研制,平台的机械结构可以保证在4.0 m×2.0 m×1.4 m的三维空间范围内四旋翼无人机的飞行姿态模拟与飞行轨迹的真实复现;在半物理仿真平台底部放置具有不同军事场景纹理信息的仿真沙盘,实现真实飞行场景模拟,利用控制系统可按比例在室内开展飞行模拟实验;仿真平台的控制系统基于EtherCAT总线,保证反馈的实时性,同时基于Qt与Open Inventor软件开发了无人机实时飞行动画模拟系统,实现了飞行轨迹实时显示。

1 四旋翼无人机特性和动力学模型

首先建立四旋翼无人机的动力学模型,分析其运动规律。接着根据飞行特性,设计合适的机械结构并进行力学性能分析。

1.1 四旋翼无人机动力学模型

如图1所示,建立惯性坐标系OXYZ以及四旋翼坐标系O′rio,图1中M1、M2、M3和M4分别表示四旋翼各个轴上的驱动电机,F1、F2、F3和F4分别表示4个电机产生的升力。

图1 四旋翼无人机力学分析

为了简化计算,将惯性坐标原点与无人机坐标系原点重合。根据四旋翼无人机的飞行动力学可以得出四旋翼的姿态方程[18]为

(1)

式中:φ为横滚角;θ为俯仰角;ψ为偏航角;Ixx、Iyy和Izz分别为四旋翼无人机在其坐标系下的各轴转动惯量;L为电机旋转中心到四旋翼坐标系原点的距离;τ为转动空气阻力系数;j=1,2,3,4,表示对应的M1、M2、M3、M4;ωj为各旋翼电机的旋转速度,j=1,2,3,4。

无人机位置数学模型为

(2)

式中:ρ表示升力系数;m为无人机的质量;k1、k2和k3分别为沿r轴、i轴和o轴方向的空气阻力系数;d1、d2和d3表示无人机沿着r轴、i轴和o轴方向的系统扰动;g为重力系数。

由式(1)、式(2)分析可知,四旋翼无人机在三维空间内,只要其运动状态发生改变,其姿态也要随之改变。因此,为了模拟无人机的飞行,需要设计出在一定空间内具有6自由度的机械结构。

1.2 机械结构设计

为了更好地进行无人机的试验,本文在传统三轴转台的基础上增加了三轴桁架,使其具备3个方向的直线位移能力,搭建可以在一定空间内拥有6自由度的无人机仿真平台。其三维结构如图2所示。

图2 机械结构

在模拟四旋翼无人机飞行时,由于三轴转台末端需要搭载光学前端,且转台在运转时会受到转动惯量的影响,对转台的结构强度提出了一定的要求。如图3(a)所示的传统三轴转台大多是放置在地面上的,如果采用增大机架体积的方法来保证其结构强度,则会导致转台质量增加。本文对传统转台结构进行改进,在不改变其承载能力的情况下实现轻量化设计,如图3(b)所示。当三轴转台悬挂在桁架上转动时,外框架所承受的载荷最大,对其进行有限元分析可以得到图4所示的结果,在承受最大载荷时,其末端形变仅为1.14×10-7mm,力学性能满足高精度仿真的需求。

图3 转台机械结构图

1.3 耦合动力学模型

本文设计的仿真平台机械结构主要由三轴桁架系统和三轴转台系统两个子系统组成,如图5所示。

三轴转台系统的3个旋转框架之间存在耦合关系,彼此之间的运动相互影响。耦合主要包括惯量耦合和动力学耦合。惯量耦合是指在转台运动期间,其转动惯量在一定范围内变化;动力学耦合是指各框架之间惯性力矩的交叉耦合和陀螺效应。因此需要对各轴之间的耦合进行计算。图6表示三轴转台3个轴之间的坐标关系,其中OXrYrZr为横滚轴坐标系,OXiYiZi为俯仰轴坐标系,OXoYoZo为方位轴坐标系,α为横滚轴绕OZr的旋转角,β为俯仰轴绕OYi的旋转角,γ为方位轴绕OZ的旋转角。

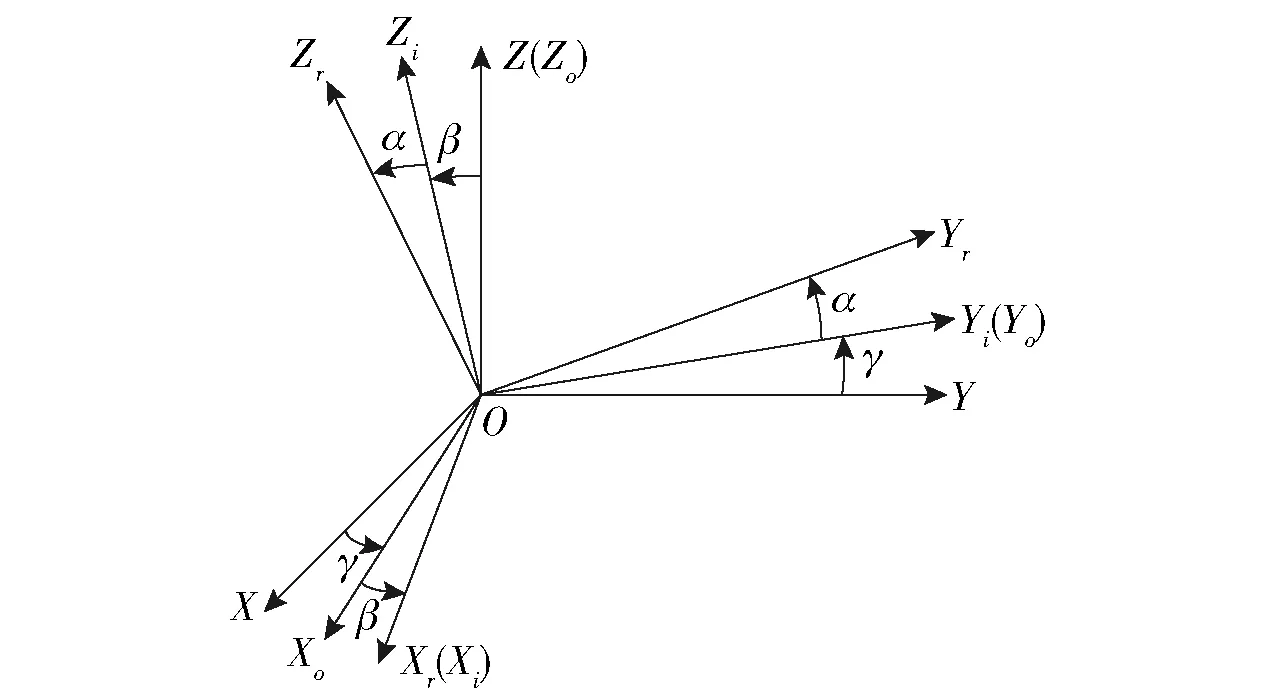
图6 三轴转台坐标变换示意图

3个转轴的转动惯量矩阵分别为

(3)

(4)

(5)

首先分析横滚轴,其中横滚轴的安装是对称的,其框架惯量积为0 kg·mm2,因此其转动惯量可以简化为

(6)

根据计算得到横滚轴坐标系相对于俯仰轴坐标系的转动惯量矩阵:

(7)

式中:Pri为横滚轴坐标系OXrYrZr投影到俯仰轴坐标系OXiYiZi的转移矩阵,

(8)

因此,横滚轴框架相对于俯仰轴OYi的转动惯量为

JYri=JYrcos2α+JZrsin2α

(9)

同理,可以计算得到横滚轴坐标系相对于方位轴OZo的转动惯量为

JZro=JXrsin2β+JYrsin2αcos2β+
JZrcos2αcos2β

(10)

俯仰轴相对于方位轴的转动惯量为

JZio=JXisin2β+JZicos2β-JXiZisinβcosβ-
JZiXisinβcosβ+JXisin2β

(11)

这样,横滚轴坐标系相对于轴OXr的转动惯量为

JOXr=JXr

(12)

通过计算可以得到俯仰轴框架结构(包括横滚轴框架结构)相对于俯仰轴OYi的转动惯量,即

JOYi=JYri+JYi=
JYi+JYrcos2α+JZrsin2α

(13)

由此可以推导出方位轴框架结构(包括横滚轴和俯仰轴的框架结构)相对于方位轴OZo的转动惯量为

JOZo=JZo+JZio+JZro=JZo+JXisin2β+JZicos2β-
JXiZisinβcosβ-JZiXisinβcosβ+JXisin2β+
JXrsin2β+JYrsin2αcos2β+JZrcos2αsin2β

(14)

三轴相对各转动轴的转动惯量近似值如表1所示。

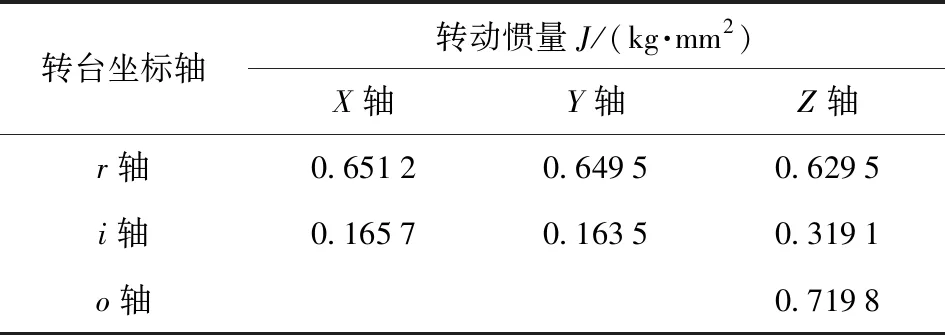
表1 三轴相对各转动轴的转动惯量近似值

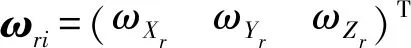
(15)

式中:Pio为坐标系OXiYiZi投影到坐标系OXoYoZo的转移矩阵;Pog为坐标系OXoYoZo投影到坐标系OXYZ的转移矩阵。

当方位轴以角速度γ旋转时,横滚轴相对于大地坐标系产生的角速度矢量为

(16)

式中:Pro为坐标系OXrYrZr投影到坐标系OXiYiZi的转移矩阵。

当俯仰轴以角速度γ旋转时,横滚轴相对于大地坐标系产生的角速度矢量为

(17)

式中:ωi为俯仰轴相对于大地坐标系的角速度。

根据矢量迭加原理可知,横滚轴所在坐标系相对于大地坐标系的角速度ωr,等于方位轴所在坐标系相对于大地坐标系的角速度ωo、俯仰轴所在坐标系相对于方位轴所在坐标系的角速度ωio,与横滚轴所在坐标系相对于俯仰轴所在坐标系的角速度ωri所引起的横滚轴结构相对于大地坐标系的矢量和:

(18)

同理,俯仰轴所在坐标系相对于大地坐标系的角速度ωi等于方位轴所在坐标系相对于大地坐标系的角速度ωo,与俯仰轴所在坐标系相对于方位轴所在坐标系角速度ωio所引起的俯仰轴结构相对于大地坐标系的矢量和:

(19)

设H为刚体的动量矩,则

H=HXi+HYj+HZk=
JXωXi+JYωYj+JZωZk

(20)

式中:HX、HY和HZ分别表示刚体在X轴、Y轴和Z轴上的动量矩;i、j和k为X轴、Y轴和Z轴上的单位向量。

根据哥氏转动定理,得到

(21)

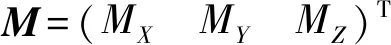
(22)

联立式(21)和式(22),得到刚体的欧拉动力学方程为

(23)

综合求得:

(24)

(25)

(26)

1.4 交流伺服电机数学模型

交流伺服系统具有高转矩比,能够实现系统的快速起动以及制动。本文所选电机为永磁交流伺服电机,根据文献[19]得到电机的力矩公式:

(27)

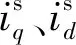
Td=Pmψris

(28)

由于Pmψr为电机常数,力矩公式简化为

Td=kis

(29)

式中:k为交流伺服电机的力矩常数,查阅电机产品手册可知,横滚轴与俯仰轴的力矩常数为4 kg·fm/A,偏航轴的力矩常数为4.2 kg·fm/A。此时交流电机可以简化成直流电机模型,从而实现三相永磁同步电机的控制参数解耦,达到矢量控制的目的。联立式(24)～式(26)和式(29),忽略极小量,可得

(30)

(31)

(32)

式中:Ir、Ii、Io分别表示横滚轴、俯仰轴以及方位轴电机的输入电流。设

(33)

则三轴转台的动力学系统可以转换成如下形式:

(34)

(35)

(36)

由此可以看出,三轴转台是一个三输入、三输出的非线性系统,并且各个转轴之间相互耦合。因此,为了提高控制精度,需要对系统进行解耦计算。

1.5 解耦设计

根据文献[20]可知,本文系统可以通过状态反馈和动态反馈补偿解耦。对于式(34),设

(37)

则有

(38)

(39)

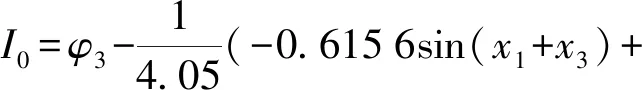
(40)

将式(38)～式(40)作为动态补偿和状态反馈解耦网络串联在式(34)之前,则可以将系统化为

(41)

(42)

(43)

此时系统为输入为φ1、φ2、φ3以及输出为y1、y2、y3的单输入单输出系统。将解耦网络串联在控制网络之中,如图7所示。

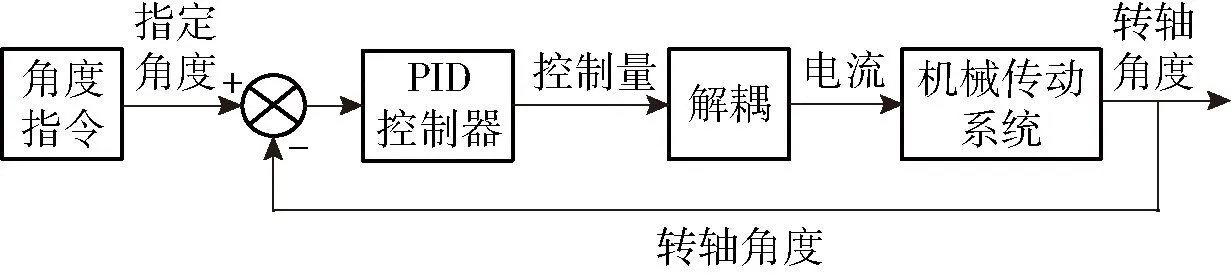
图7 解耦控制方案

2 控制系统设计

四旋翼无人机视觉导航半物理仿真平台设计中最重要的一环是伺服控制系统。控制系统要求响应快、精度高、鲁棒性好,为此本文选择基于EtherCAT总线进行实时控制系统的设计。

2.1 总体结构

本文系统为多轴同步协同工作,以实现无人机飞行的模拟。如图8所示,控制系统由工作站、英国翠欧TRIO公司PC-MACT EtherCAT总线控制器、日本哈默那科公司生产的哈默那科伺服电机组成。工控机上搭载着上位机,通过Ethernet和TRIO PC-MCAT总线运动控制器相连。运动控制器通过EtherCAT与I/O拓展器连接,以实现同时与6台伺服电机驱动器相连,这样可实现6台电机同时转动,达到模拟飞行姿态的效果。伺服电机使用日本哈默那科AC伺服电机,其拥有独一无二的小型化设计以及中空孔结构。执行元件中央的贯通孔内可穿过配线、配管、激光等,简化了机械装置的整体构造。

图8 控制系统总体架构

针对四旋翼无人机仿真系统的控制模块,本文系统将各轴独立供电,并设计过载保护以及漏电保护。其桁架与转台的电气设计如图9所示。

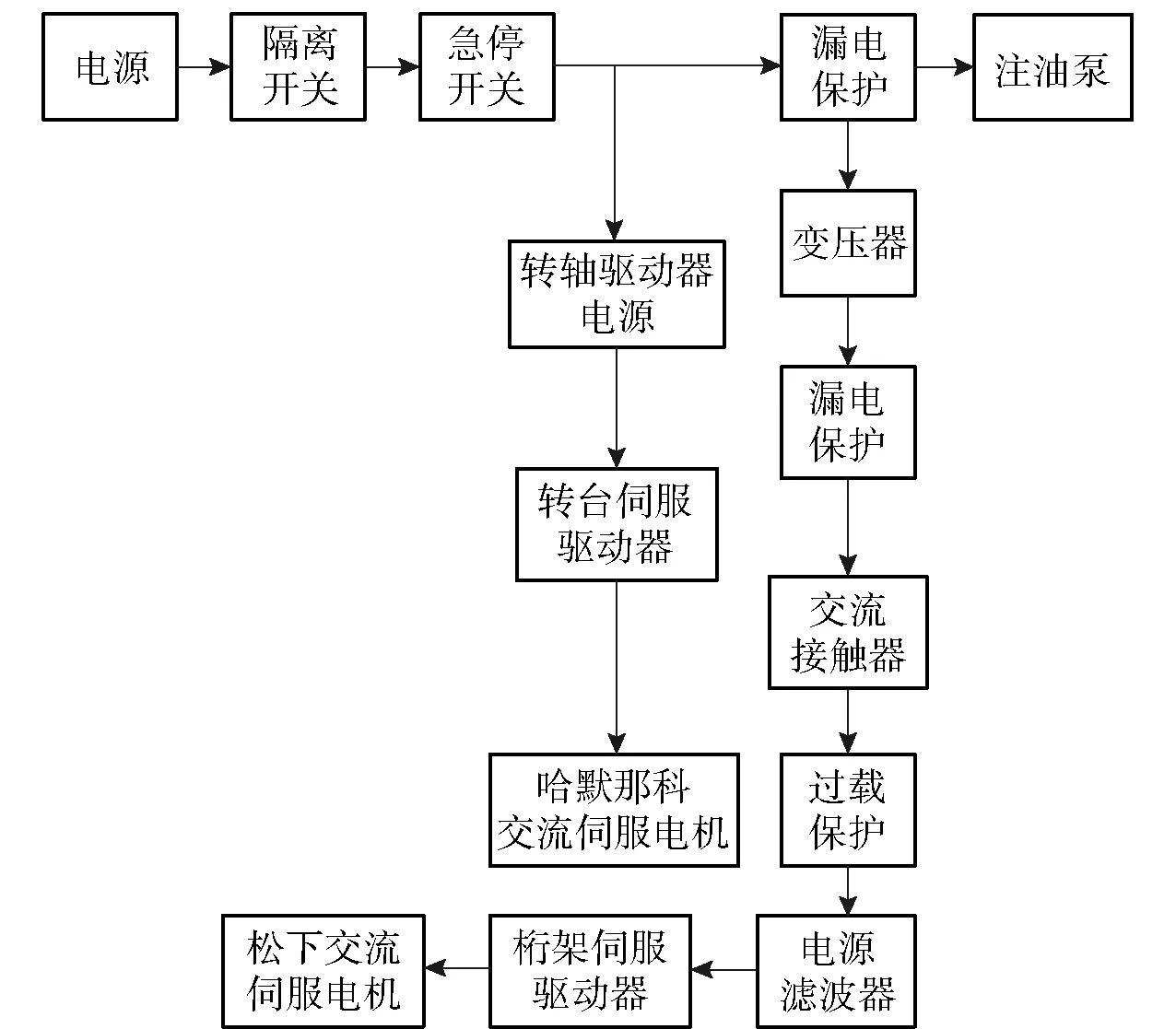
图9 电气连接示意图

2.2 电机负载

表2所示为三轴桁架的主要参数,Z轴的负载最大,达到2 918.7 N,其中减速机的速比为7。经计算,电机所承受的最大力矩为8.85 N·m,最大速度为2 519.98 r/min。考虑到安全系数比,本文系统选用日本松下公司生产的MHMF402L1型电机。该电机最大输出力矩达57.3 N·m,力矩利用率为33%;最大速度为3 000 r/min,速度利用率为84%,可以为Z轴提供稳定的动力。同理,X轴与Y轴分别选用日本松下MHNF152L1型与MHMF03L1型伺服电机。表3为三轴转台架的主要参数。

表2 三轴桁架主要参数

表3 三轴转台架主要参数

由表3可以计算出角速度设计参数20(°)/s,换算成弧度,角速度ω为

(44)

若加速曲线按梯形加减速曲线,则对于快速运动的机械结构,其加速时间不应超过0.1 s。因此加速时间tac设为0.05 s,从0(°)/s加速到20(°)/s。这时加速度ωac为

(45)

转台的加速转矩Tac为

Tac=Ixx×ωac=1.043×6.978=7.278 N·m

(46)

考虑到转台的负载转矩TL=0 N·m,转盘旋转时轴承的摩擦转矩较小,可忽略不计,若电机的机械传动效率η=0.9,则电机的转矩TM为

(47)

对于快速运动、频繁启停的电机,还需要校核等效转矩。考虑最极限的情况,转台从正极限转到负极限,再转回到正极限,作为运行周期。由于转台的负载转矩TL=0 N·m,显然当匀速运动时间为0 s时平均转矩最大,由于负载转矩为0 N·m,估计等效转矩仍然为加速转矩。等效转矩TRMS可以表示为

(48)

针对转动的功能需求,本文系统选用日本哈默那科公司生产的SHA25A101S一体化AC伺服执行元件。由于该驱动模块采用减速比为101的谐波减速器,电机具有较大的等效转动惯量。该电机可以提供约70 N·m的连续工作的转矩,可以满足转台转矩的要求。由于o轴在三个转轴中承受的载荷最大,其他两轴采用同型号电机也能够满足性能需求。

2.3 系统搭建

从控制系统架构可以看出,对于各轴电机运作时,对其同步性、实时性以及精确度都有着极高的要求。EtherCAT总线控制技术,其数据传输速度可以达到100 Mbit/s,是最快的工业以太网技术;同时其对于数据帧的处理实时性很高,数据刷新周期小于100 μs,结合高精度的分布式时钟,可以保证各从站节点设备的同步精度小于1 μs。

因此,本文选取英国翠欧公司生产的EtherCAT总线控制器PC-MCAT作为运动控制器。三轴转台部分选用美国科普利驱动器,该驱动器基于EtherCAT通信,且拥有极高的分辨率的A/D转换器,可确保最佳的电流环路性能。三轴桁架部分采用日本松下公司生产的MDDLNT55BF驱动器与其配套伺服电机。与此同时,在直线导轨上安装英国雷尼绍公司生产的HK-0400-0002光栅,反馈实时位置数值。系统实物如图10所示。图10中,三轴桁架下方空间搭建特种环境沙盘,用于模拟各类军事场景航拍纹理,如图10(c)所示。

图10 系统实物图

2.4 控制系统软件架构

平台应用软件分为控制模块和飞行模拟模块。如图11所示,控制模块主要基于TRIO PCMACT运动控制卡的底层控制指令,基于VS2017以及Qt软件平台实现一些基本的运动控制功能,以及无人机的姿态信息,转换成TRIO BASIC语言并执行。飞行模拟模块将仿真平台所传回来的各轴信息,转换成无人机动画飞行模拟。

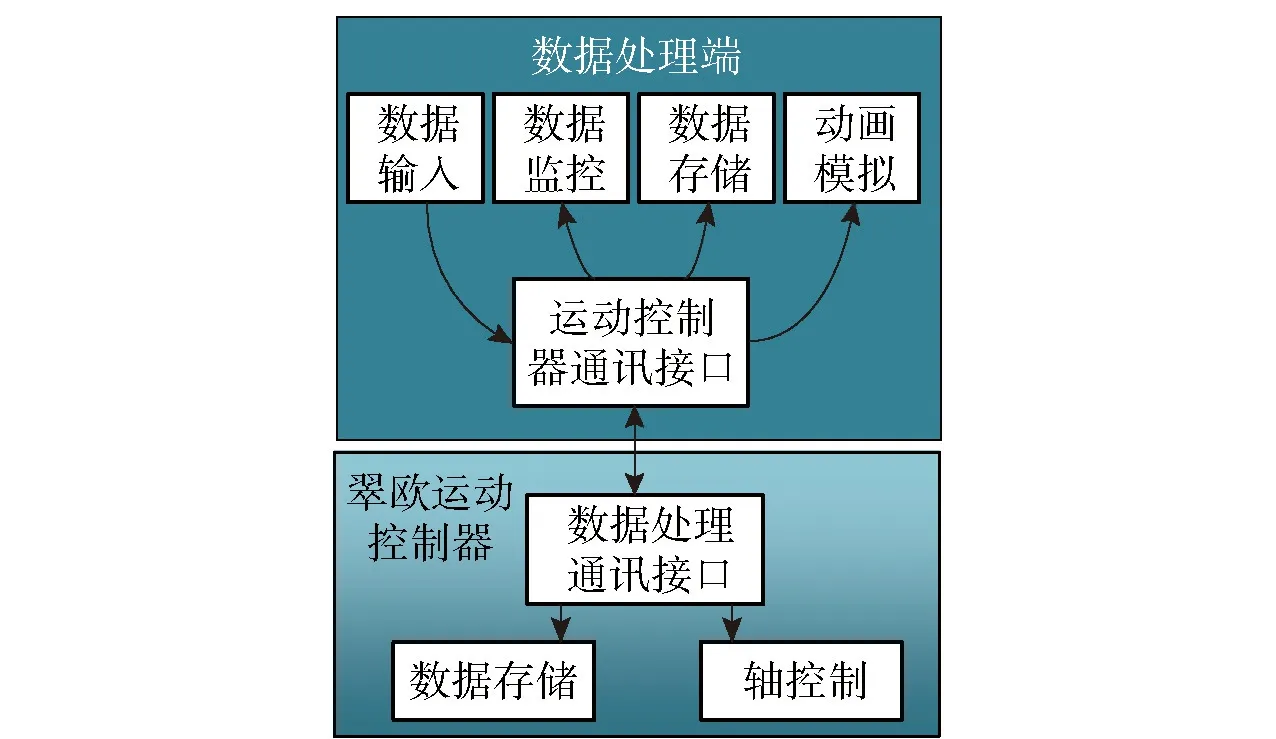
图11 软件架构

如图12所示,本文仿真系统可以实现对城市场景的三维地图模拟,同时对实时飞行轨迹进行显示。

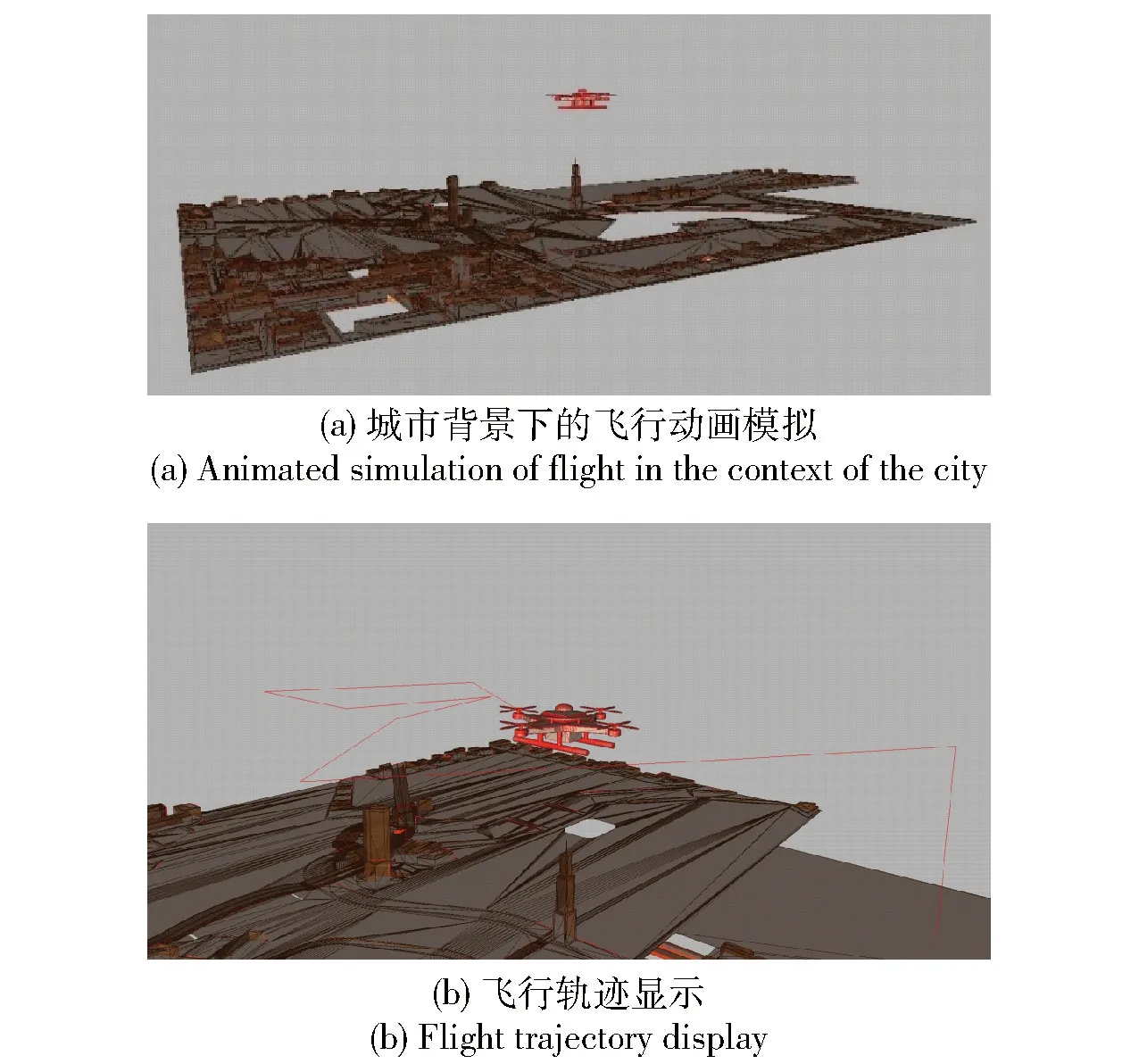
图12 实时动画模拟

图13所示为上位机程序运行流程图。采用多线程并行的思路,将数据显示、飞行动画模拟、姿态计算以及指令转换各自安置在所开辟的子线程中运行,各个线程之间通过Qt软件平台的槽信号进行数据通讯,保证了软件运行的流畅性。其中线程2基于Open Inventor软件,将仿真平台各个信息转换成无人机飞行姿态以及所模拟场景的空间位置,并显示飞行轨迹。

图13 软件流程图

3 仿真平台精度测试及仿真实验

对仿真平台的重复定位精度、累计定位精度以及动态性能进行测试验证,同时开展室内外飞行对比验证。

3.1 稳态性能测试

为了测试仿真平台的稳态性能,本文采用激光干涉仪对三轴桁架的直线轴运行范围、重复定位精度、累积定位精度、直线轴运行速度、直线轴运行加速度,以及三轴旋转平台的旋转轴运行范围、重复定位精度、转轴运行速度、转轴运行加速度进行测试。

三轴桁架精度测试方法:在X轴、Y轴和Z轴正负方向上循环连续测量。对每个目标位置在每一方向做3次趋近,用激光干涉仪测得实际到达位置,并计算出位置偏差。对于累计误差,在某一轴上运动确定初始目标位置,并移动运动部件1 000 m,运动部件回到初始目标位置,用激光干涉仪测得实际到达位置,并计算位置偏差即为累积定位精度。

三轴转台精度测试方法:用激光干涉仪和配套分度台校准回转轴线,将分度台安装在旋转轴线的中心位置,调整分度台与回转轴的回转中心一致,使其径向圆跳动值不大于0.02 mm。将角度反射镜安装在分度台上,使角度反射镜面与激光光束垂直,并将角度干涉镜安装在光路中,与角度反射镜等高平行,平移激光头使激光光束准直。设置控制系统的转动速度,并确定目标位置、越程量、在目标点的停顿时间和循环次数。在r轴、i轴和o轴正负方向上循环连续测量。对每个目标位置在每一方向做3次趋近,由激光干涉仪测得实际到达位置,并计算出位置偏差。

图14为三轴桁架重复定位精度。由图14可知,对X轴、Y轴和Z轴分别进行重复测量3次,X轴重复定位精度可达0.033 mm,Y轴重复定位精度为0.012 mm,Z轴重复定位精度为0.004 mm。

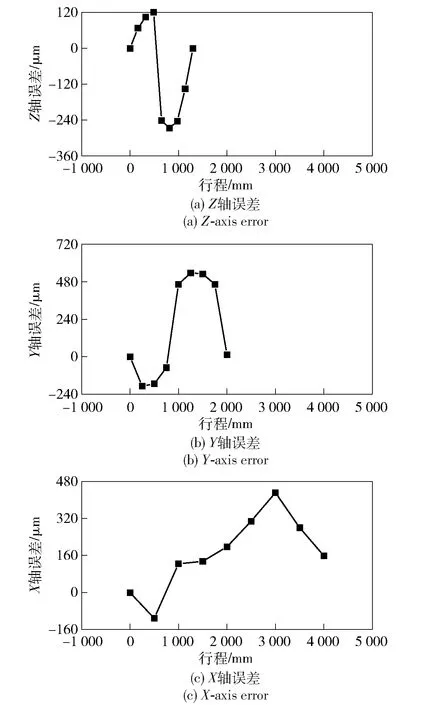
图14 三轴桁架重复定位精度

图15为三轴转台重复定位精度。由图15可知,对r轴、i轴和o轴分别重复测量3次,r轴重复定位精度为0.002°,i轴重复定位精度为0.002°,o轴重复定位精度为0.006°。

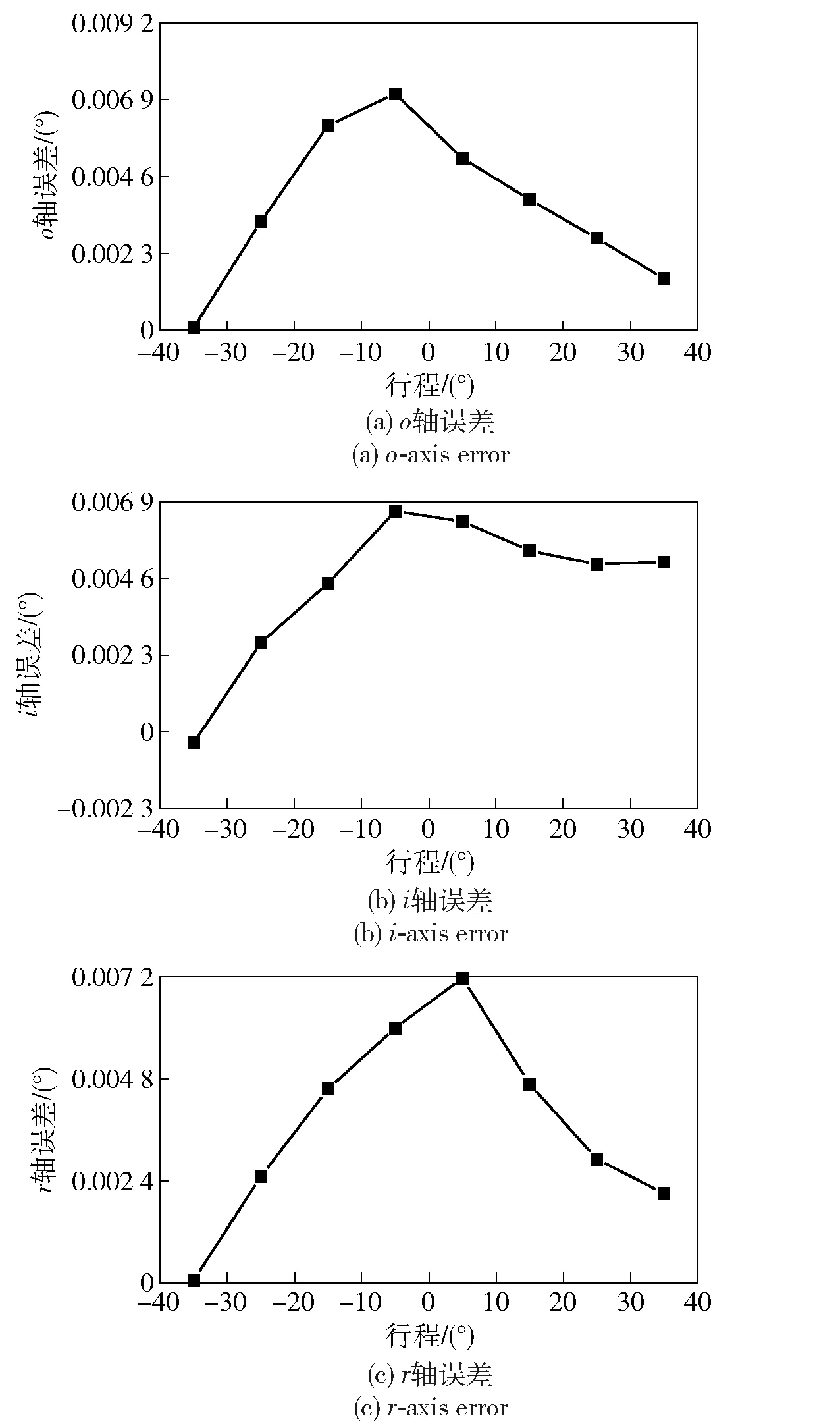
图15 三轴转台重复定位精度

3.2 动态性能测试

如图16所示,选定一条模拟飞行轨迹,将其转换成TRIO BASIC指令后,读取得到实际轨迹图。经过测量计算,三轴桁架的动态误差为0.4 mm。

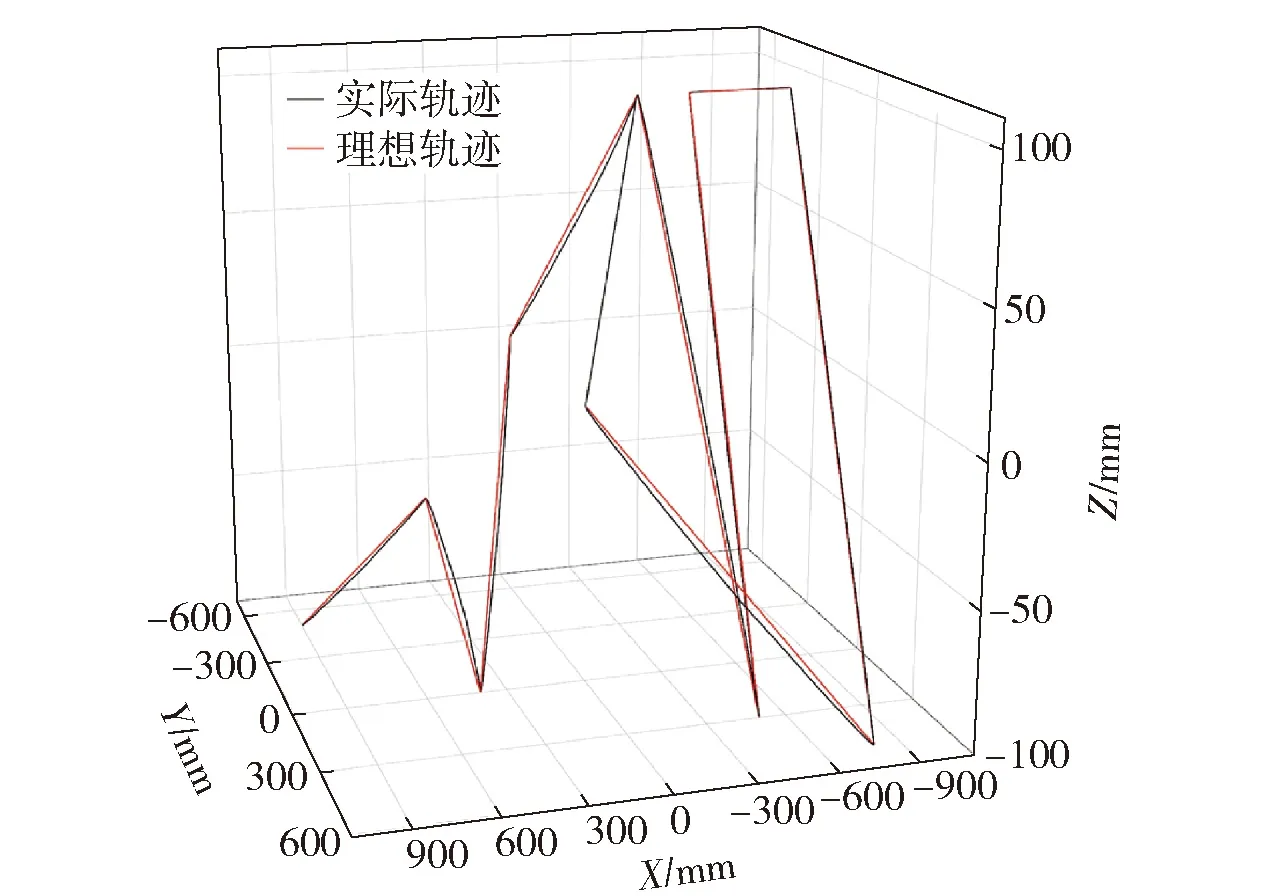
图16 三轴桁架动态轨迹图

为了更直观地表示三轴转台动态旋转角误差,本文将3个轴的角度用三维空间坐标表示,如图17所示。经过测量计算,三轴转台的动态旋转角误差可以控制在0.04°以内。

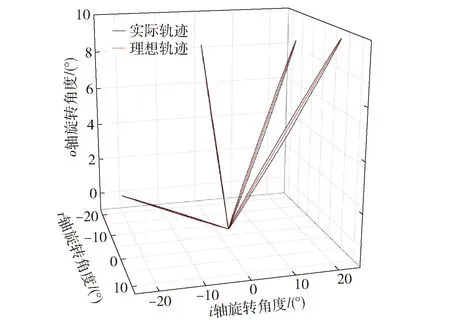
图17 三轴转台动态旋转角度图

3.3 室内外对比试验

在完成室内视觉导航算法仿真后,需要在室外真实环境下使用无人机进行算法验证。本文使用的无人机为自主研发设计的基于Pixhawk飞控的四旋翼无人机,机身质量为2.95 kg,轴距680 mm,最大起飞负载4 kg,最长飞行时间20 min。

使用半物理仿真平台进行视觉导航后的仿真轨迹和室外进行视觉导航后的真实飞行轨迹,如图18所示。室内外飞行存在地图缩放,室内地图与室外地图的缩放比为1∶100。将室外仿真轨迹按比例进行缩小后与室内飞行轨迹进行比较,平均误差约为0.05 m,该结果表明半物理仿真平台能够有效地实现无人机视觉导航仿真。

图18 仿真效果对比

4 结论

本文提出一种基于实时控制系统的6自由度四旋翼无人机视觉导航半物理仿真平台,机械机构包含三轴桁架和三轴转台,同时基于EtherCAT总线构建实时控制系统。通过Qt与Open Inventor软件将6轴的位置与角度信息转换成无人机飞行动画,实现实时轨迹跟踪。三轴转台的重复定位精度达到0.006°,三轴桁架的重复定位精度达到0.033 mm,6轴联动时动态误差精度可达0.04°和0.4 mm。该系统能够很好地满足四旋翼无人机视觉导航的仿真测试需求,加速了视觉导航算法的优化迭代,降低室外导航算法测试的成本。未来该平台可为伪装目标识别、动态目标追踪等军事试验任务提供有力支撑。