基于身份匈牙利算法的无人机蜂群分布式目标分配方法
2023-10-07刘兴宇郭荣化任成才闫超常远周晗相晓嘉
刘兴宇, 郭荣化, 任成才*, 闫超, 常远, 周晗, 相晓嘉
(1.32399部队, 江苏 南京 210046; 2.国防科技大学 智能科学学院, 湖南 长沙 410073; 3.军事科学院, 北京 100091)
0 引言
无人机蜂群作战是未来无人作战领域的重要作战样式[1]。无人机蜂群可以对广域多个目标进行分布式并行攻击,其中的关键在于如何为蜂群个体选择打击目标,使得整体打击效果最优。蜂群并行攻击的多目标匹配问题需要考虑通信距离、感知距离等约束的限制,其攻击效能也受到攻击角度、攻击速度、攻击距离、攻击强度等因素的影响,具有很强的挑战性。
当前,已经有诸多学者对多目标分配问题开展了研究。针对多目标分配问题模型,孙永芹等[2]首先提出了无人机的自主优先权和协同优先权概念。兰俊龙等[3]进一步建立了目标威胁模型。肖冰松等[4]在建立攻击任务分配模型的同时考虑了探测任务的分配问题。胡月等[5]在模型中利用Vonoroi图添加了对于目标航迹路径代价的考虑。韩统等[6]在模型中构建了描述友方相互之间产生态势威胁增幅的协同威胁指数模型。Kong等[7]在模型中考虑两个实际且相互冲突的目标,即最大化作战效益和最小化武器成本。Kim等[8]认为发射器和目标之间的航向误差对命中概率影响极大,必须考虑航向误差来建立模型以反映更真实的交战情况。由此可见,对于无人机协同攻击多目标问题的研究在不断深入,建立的模型不断贴合实际应用。作战过程中的打击目标往往包括多种目标如指挥所、步兵战车、坦克等,这些目标的重要程度不同,但是当前大部分模型并未区分目标的重要程度,难以实现整体作战效能的最优。
多目标分配算法可以分为传统算法和智能算法。智能算法包括基于优化的算法、基于神经网络的算法等。李战武等[9]将并行遗传算法(GA)与分布估计算法相结合,提出并行分布GA,对多目标攻击决策问题进行了求解。岳源等[10]运用离散粒子群优化(PSO)算法对目标分配模型进行了优化求解。Kline等[11]提出一种非线性分支定界算法,对静态目标分配问题进行了求解。吴文海等[12]采用平衡差分进化算法,基于自适应参数整定方法更新了算法参数。黄刚等[13]提出一种新的近似聚类混合双策略差分进化算法,对多无人机协同目标分配最优问题进行了求解。孙永芹等[2]在超视距多机协同多目标攻击系统中使用BP神经网络完成了目标分配。朱建文等[14]构建了基于强化学习的多目标决策架构,利用Q-Learning方法对协同攻击方案进行了智能决策。Nan等[15]建立了强化学习框架,并利用动态规划方法将动态目标分配问题分解为多个静态组合优化问题。优化算法以及神经网络具有设计模式化、通用性强等优点,但是存在求解过程耗时长、易陷入局部最优解等缺陷,无法满足战场环境下实时性、可靠性等要求。
拍卖算法和匈牙利算法(HA)是两种经典的求解多目标分配问题的传统算法。拍卖算法由Bertsekas[16]提出,该算法模拟了拍卖过程,通过重复多次拍卖来确定最终的目标分配方案。拍卖算法具有计算量小、实时性强等优点,但其算法性能与其报价增长幅度有关,无法保证获得唯一的最优分配结果。HA由匈牙利数学家Konig设计[17-18],该算法基于独立零元素定理,仅采用矩阵变换等操作就能求出模型最优解,具有结果稳定、计算量小的优点[19-20]。柳毅等[21]把HA推广至多对多的目标分配问题中,仿真结果表明HA对于多目标分配问题的求解十分有效。Du等[22]在HA中引入特殊的权重因子,计算了个体对各目标的成本和收益。张进等[23]提出统一效率矩阵,创建了可适用于所有类型目标分配问题的可适应HA。Jiang等[24]在HA的基础上融合遗传算法(GA)提出了匈牙利融合GA,将匈牙利算法求出的可行解作为GA初始种群中的精英个体。随着计算机技术的不断发展,HA结果稳定、求解迅速的优势愈发突出[19-20]。
然而,当前包括HA在内的多目标分配算法无法直接适用于无人机蜂群的作战场景,原因主要有以下两方面。一是当前多目标分配算法主要面向信息全局可知的集中式分配,目标分配由控制基站完成。控制基站同时掌握我方所有武器信息以及敌方所有目标信息,并具有强大的计算能力,能够迅速为我方各武器分配打击目标。但是,无人机蜂群不存在中心节点,需要蜂群个体在任务过程中进行实时智能自主决策。二是无人机个体通信范围有限,只能依据周围邻居信息进行决策,并且不同蜂群个体掌握的情报信息不一致。将当前的多目标分配算法应用于无人机蜂群,可能导致冗余攻击或者打击遗漏。打击遗漏是指无人机1号视角下,目标1号应该由无人机2号打击,无人机2号视角下,目标1号应该由无人机1号打击,这样便会导致目标1号不在打击目标序列之内。
当前也存在部分关于分布式目标分配方法的研究,但无法完全适配于无人机蜂群。岳源等[10]提出了分布式多无人机协同侦察目标分配方法,该方法的分布式只是强调无人机个体进行自治,认为无人机集群可以通过数据链共享各无人机信息及相应目标信息,与无人机蜂群个体仅掌握局部邻居信息相违背。林晨[25]针对无人机集群的任务分配问题提出了分布式拍卖算法,该方法约定了蜂群个体只能获得周围邻居信息,但其认为个体应当可以通过多次信息传递获得所有无人机的相关信息,如此做法需要极大的通信带宽,会导致极大的通信代价,与无人机蜂群个体有限通信资源、有限通信能力相违背。陈洁钰等[26]针对多无人机协同作战的动态目标分配问题,提出一种基于分布式拍卖机制的目标分配算法,该方法需要编队内各无人机共享态势信息,并通过数据链将目标信息传递给指控中心,与无人机蜂群无中心节点相违背。
针对上述情况,本文在HA的基础上提出了身份HA。一方面,身份HA区分了敌方目标身份,为不同类型的目标赋予了不同重要程度。另一方面,身份HA为蜂群个体添加了身份信息,无人机按照身份编号顺序依次选择打击目标,避免冗余攻击或者攻击遗漏。算例分析结果表明,本文所提身份HA实现了无人机蜂群的分布式目标分配,为无人机蜂群鱼贯依次打击策略的实现提供了算法支撑,提高了无人机蜂群的整体作战效能。
1 多目标分配问题描述与建模
1.1 分布式目标分配问题建模
在本文研究工作中,N架无人机分布在二维平面,其集合记为Γ={Γ1,Γ2,Γ3,…,ΓN}。无人机i的位置和速度分别记为xi∈R2和vi∈R2,i∈Γ。速度可以由模和运动方向来表示:
vi=vicosθe1+visinθe2
(1)
式中:vi表示无人机i运动速度的模;θ表示无人机i的运动方向;e1和e2为相互垂直的单位向量,如图1所示(其中ru为无人机通信半径,rs为无人机侦察与打击半径)。无人机i与无人机k之间的相对位置xik可以表示为
xik=xk-xi
(2)
式中:xk、xi分别为无人机k和i的位置。
无人机间通信能力是有限的,设Λi为无人机i的邻居集合。任务过程中,当‖xik‖≤ru时无人机i与无人机k互为邻居,k∈Λi,则i可以与k进行交互,无人机i与无人机k可以互相获得对方的速度信息、位置信息、身份信息、可打击目标信息等。蜂群个体没有其他途径获得通信范围外个体的情报信息。
M个敌方目标分布于平面,其集合记为T={T1,T2,…,TM},敌方目标位置记为xj∈R2,j∈Τ,如图1所示。蜂群无人机的侦察打击能力是有限的,其侦察打击半径记为rs,每架无人机可以侦察相对距离小于rs的敌方目标并进行打击,即需要满足‖xij‖≤rs,i∈Γ,j∈Τ。
每架无人机携带q发导弹,可以同时攻击q个不同的敌方目标,也可以对同一个敌方目标实施打击。无人机i可攻击目标序列记为Ai,实际攻击目标序列记为Ri,则有〈Ri〉=q,〈·〉表示集合元素的数目。每一个敌方目标在被p发导弹打击后,便会被彻底摧毁。令Cij表示蜂群无人机i对敌方目标j的打击优势函数值,函数值越小,优势越大,由蜂群无人机对目标的打击优势以及目标的重要程度共同决定。Cij组成的矩阵C=(Cij)N×M称为效率矩阵。
无人机蜂群对敌方目标整体打击优势值记为
(3)
式中:Xilj=1或0,Xilj=1表示蜂群无人机i的第l发导弹选择对敌方目标j实施打击,Xilj=0表示未选择。
求解无人机蜂群的分布式多目标分配问题,是指通过合理分配各蜂群个体的打击目标,使得无人机蜂群对于敌方目标的整体打击优势最大,打击优势值y值最小:
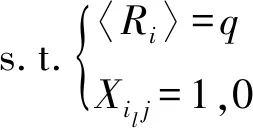
(4)
1.2 无人机对目标打击优势建模
将无人机对目标的打击优势进行建模,是多目标分配算法应用的基础。通过构造无人机对目标的角度优势、距离优势和速度优势,并且考虑打击目标的重要程度,来建模无人机对目标的打击优势函数值Cij。
无人机蜂群作战过程中,蜂群个体与敌方目标的相对几何态势如图2所示。图2中:i、j分别为蜂群无人机和敌方目标;R为目标距离;vi为蜂群无人机速度;目标视线ij,即我机与目标的连线;ω为目标方位角,规定目标方位角右偏为正,左偏为负,0°≤|ω|≤180°。

图2 蜂群无人机打击态势示意图
1.2.1 角度优势函数
令|ω|为目标方位角的绝对值,|ω|越小,导弹攻击航线越简单稳定,无人机对目标打击越准确,|ω|=0°是最佳的目标方位角。构造如下角度优势函数:
(5)
当|ω|=0°时Ta=0,达到最小值,蜂群无人机具备最佳火力打击角度;当|ω|=180°时Ta=1,达到最大值,此时目标方位角最不利于无人机攻击。
1.2.2 距离优势函数
记导弹最佳发射距离为Rdes,最远发射距离设为Rmax=rs,最近发射距离为Rmin。当蜂群无人机和敌方目标相对距离R>Rmax时,设置距离优势值Tr=1,并设置无人机对该目标打击优势为空,即蜂群无人机无法对该敌方目标实施打击;随着相对距离的减小,距离优势逐渐增大,在R=Rdes时,认为距离优势达到最大,距离优势值Tr=0;随着相对距离进一步减小,距离优势又逐渐减小,直到R=Rmin时又设置距离优势值Tr=1。基于以上考虑,从实用性与简洁性的角度出发,采用线性函数构造如下距离优势函数:
(6)
距离优势函数如图3所示。
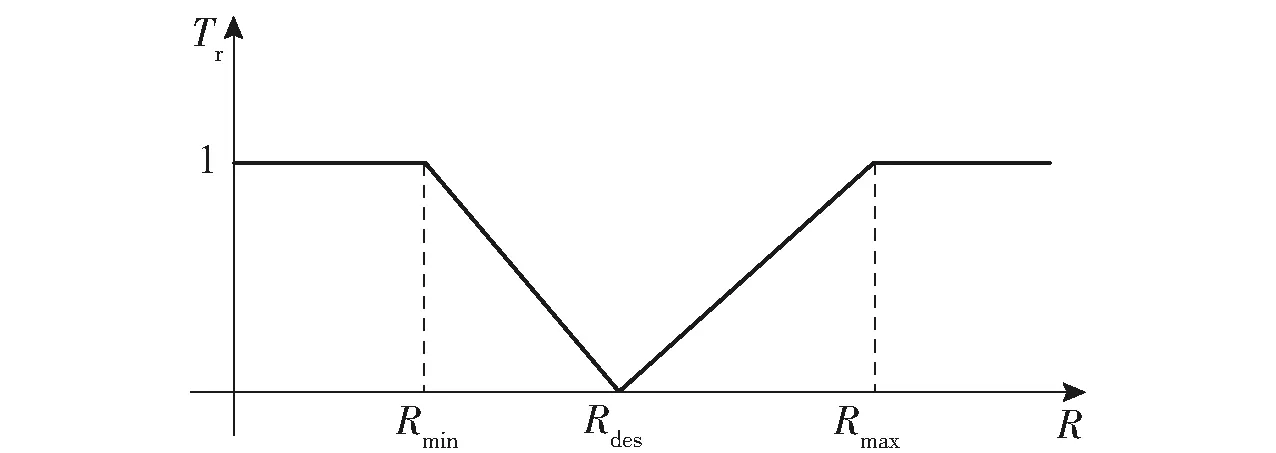
图3 距离优势函数
1.2.3 速度优势函数
蜂群无人机速度越快,作战优势越强,一方面对敌突袭可以造成出其不意的杀伤效果,另一方面可以快速摆脱敌侦察雷达锁定,避开敌火力打击。记蜂群无人机常规巡航速度为vC,最大速度为vmax。当无人机速度v小于vC/3时,认为无人机毫无速度优势,轻易便被敌火力打掉,速度优势值Tv=1;当无人机速度大于vC/3且小于vC时,无人机速度优势迅速增加;当无人机速度达到vC时,无人机已经具备一定速度优势,速度优势值Tv=0.1;当无人机速度大于vC时,无人机速度优势缓慢增加。基于以上考虑,构造如下速度优势函数:
(7)
速度优势函数如图4所示。
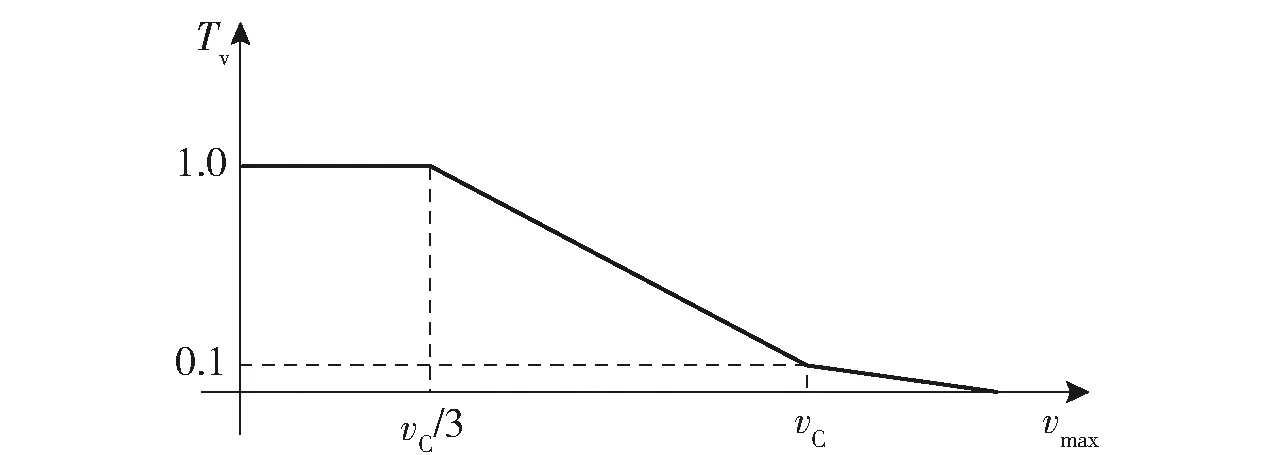
图4 速度优势函数
1.2.4 目标重要程度
作战过程中,蜂群可打击目标存在多种类型,包括敌指挥所、敌指挥控制车、敌步兵战车等。不同类型的敌方目标,重要程度不同,分配的火力规模理应不同。彻底摧毁敌核心目标是蜂群作战的最重要目的,蜂群个体选择打击目标时应格外关注敌目标的重要程度,目标重要程度对于无人机选择打击目标的影响程度应该深于其他因素。基于以上考虑,区分于其他因素采用线性函数表征,目标重要程度采用指数函数或者其他比线性函数趋势陡峭的函数进行表征,构造目标重要程度函数如下:
TD=ed
(8)
式中:d={1,2,3,…,D},D表示敌方目标的种类数目,对于最重要的敌方目标,d=1,对于最次要的目标,d=D。进行归一化处理,Td=TD/Tmax,Tmax为最大的目标重要函数值。根据加权求和法,可以得到无人机i对敌方目标j的打击优势函数Aij:
(9)
式中:ka、kr、kv分别为角度优势、距离优势和速度优势的加权系数,且ka+kr+kv=1,加权系数可依据专家经验设置。将优势值进行归一化,便可以得到效率矩阵的元素值:
(10)
式中:Cmax为无人机i效率矩阵中的最大元素值。
2 多目标分配算法
2.1 HA
HA是面向分配指派问题提出的,指派问题分为平衡指派问题和非平衡指派问题。设N为元素个数,Eij为无人机对目标的打击优势,Xij表征无人机是否对目标实施打击,则平衡问题的数学模型如下:
(11)
满足
(12)
(13)
Xij=1或0
(14)
求解指派模型式(11)~式(14),等价于从E=(Eij)N×N中选出N个元素,满足:
1) 每列中恰有1个元素被选出,以保证每个目标仅被1架无人机打击。
2) 每行中恰有1个元素被选出,以保证每架无人机仅攻击1个目标。
3) 被选中的N个元素之和最小,以保证无人机蜂群的打击优势最大。
HA步骤如表1所示。限于篇幅,步骤具体内容不在此赘述,详见文献[21]。

表1 HA步骤
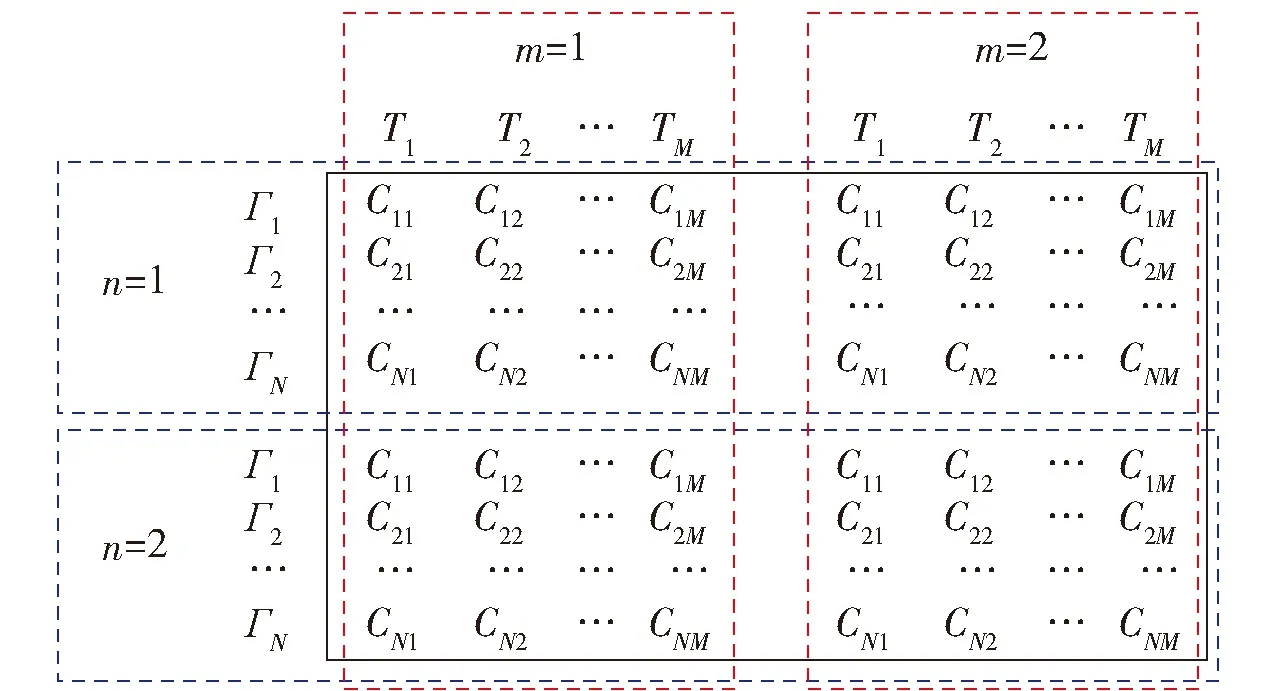
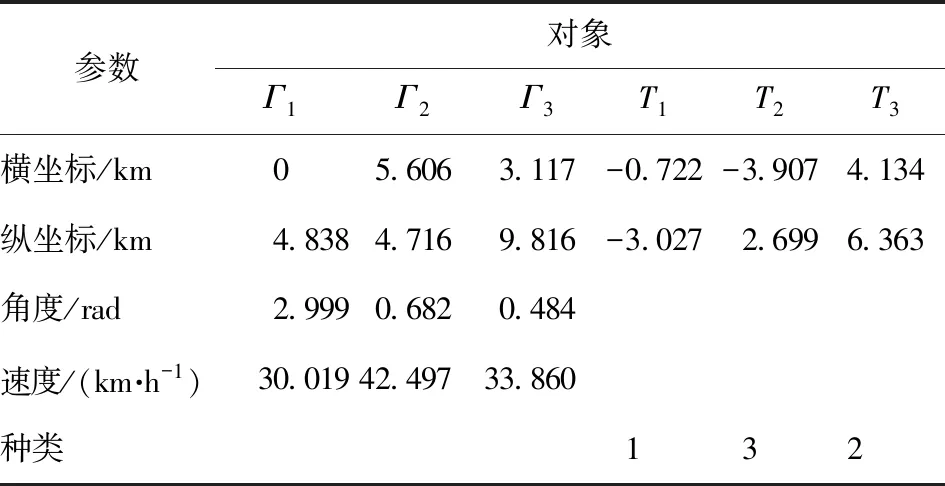
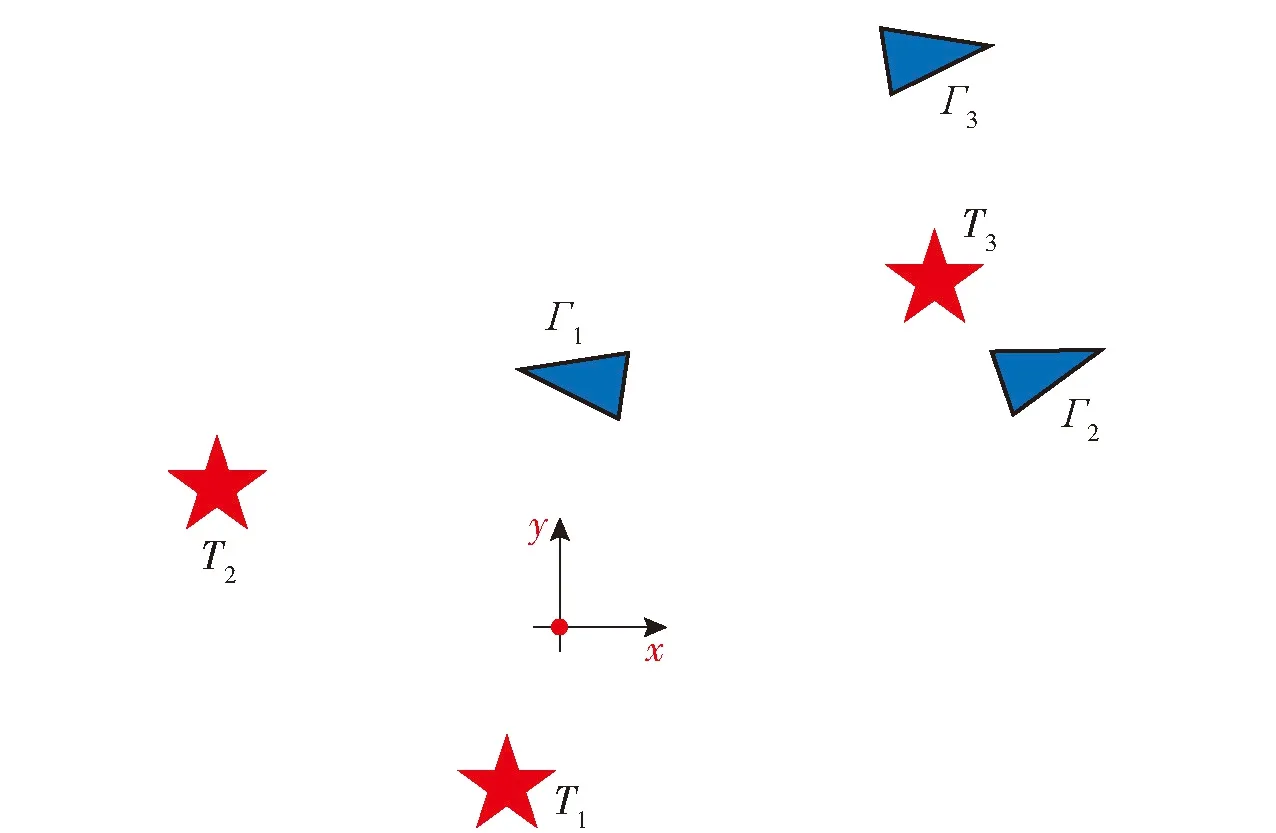
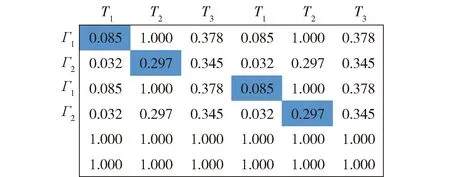
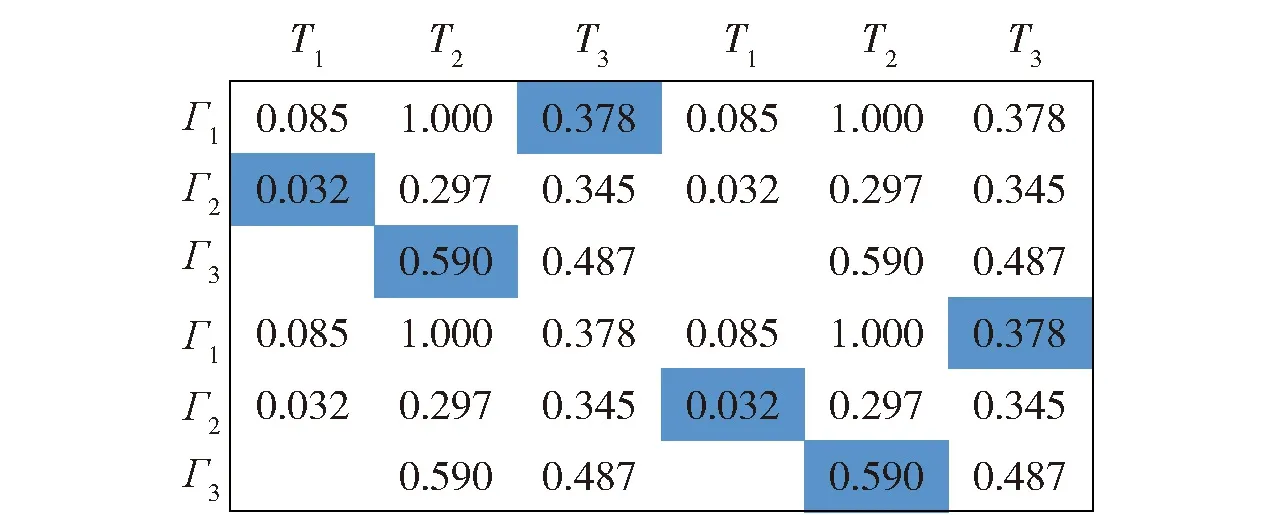
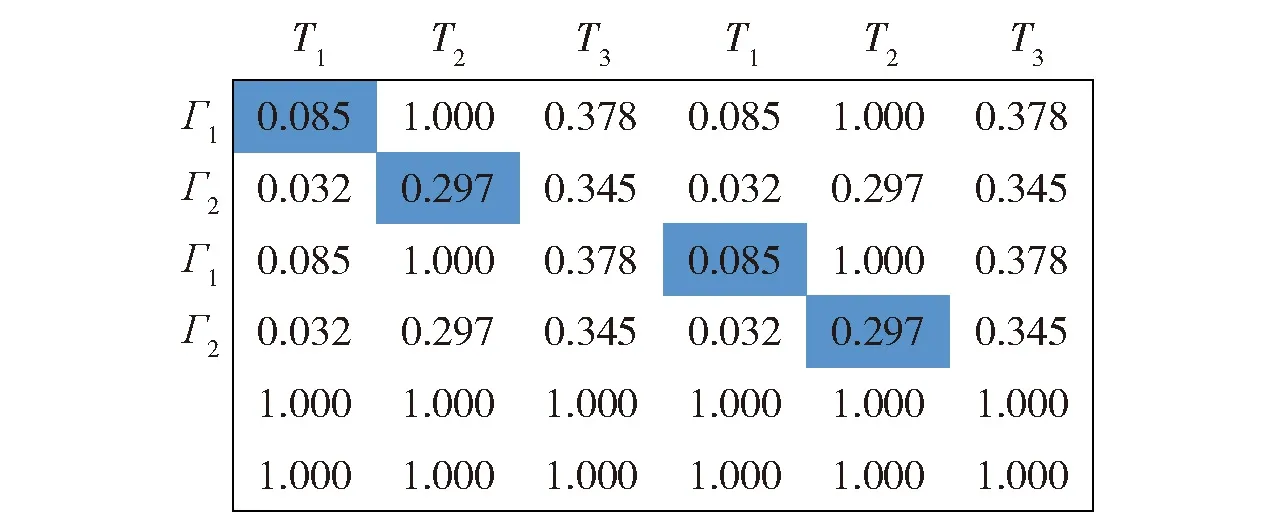
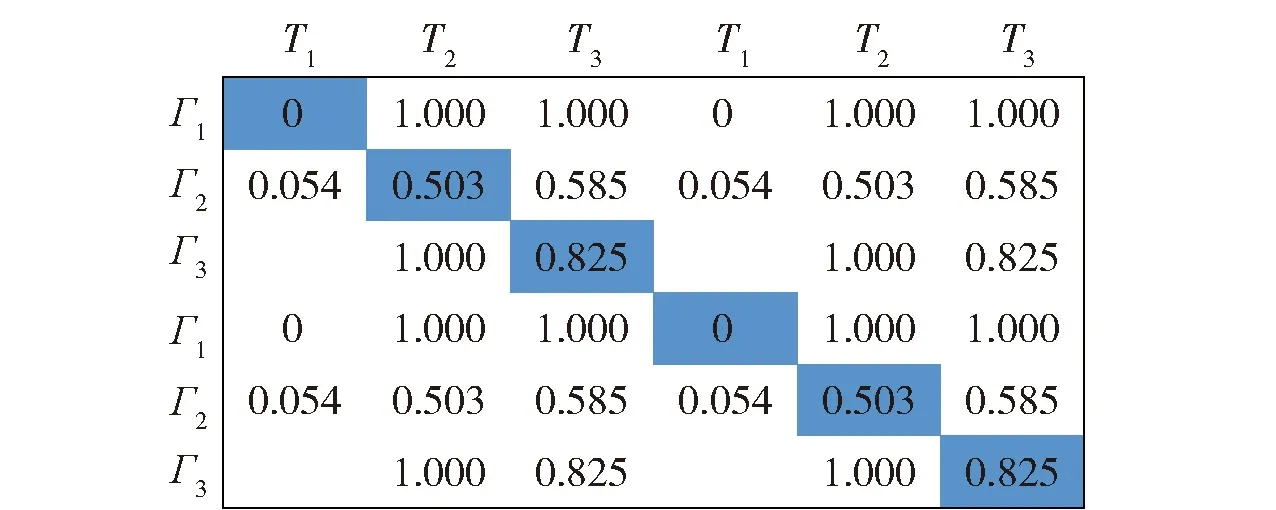
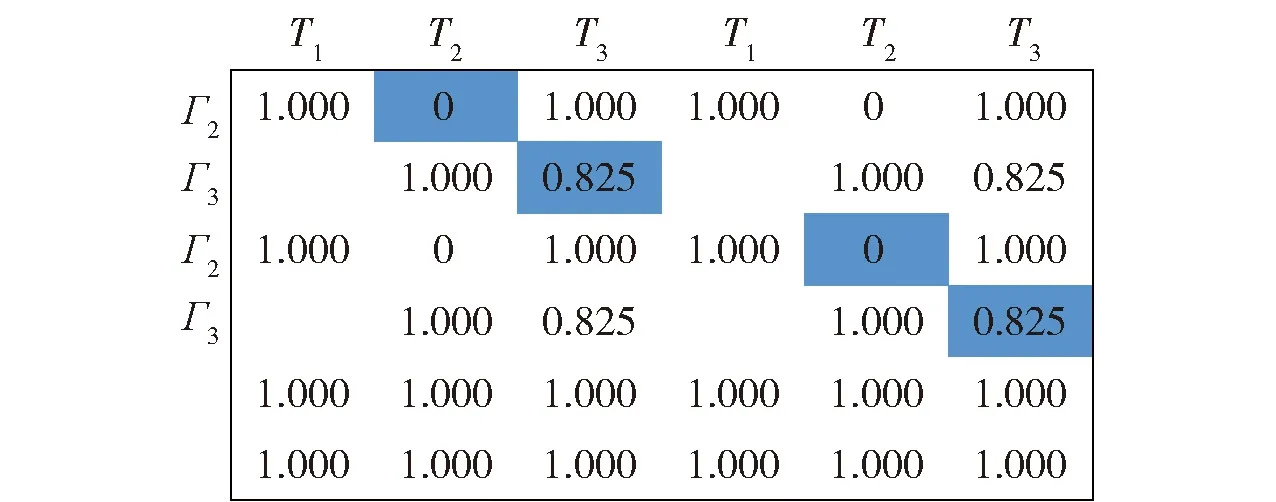
非平衡问题是指蜂群无人机数量与敌方目标数量不等,即有N架蜂群无人机攻击M个敌方目标,其中N≠M。针对非平衡问题,同样令Cij表示第i架攻击机对第j架目标机的打击优势函数值。将C=(Cij)N×M矩阵补成方阵,当N (15) 再对Q逐步应用HA,直到满足每架蜂群无人机只攻击一个敌方目标或每个敌方目标只被一架蜂群无人机的条件为止。 在HA的基础上,本文面向蜂群无人机攻击多目标场景,为蜂群无人机添加了身份信息,设计了身份HA。在改进算法中,每架蜂群无人机将编号作为自己的身份信息,与速度信息、位置信息、可打击目标信息同样,可以与周围邻居互相传输。对于无人机i,其身份信息Di=i,i∈Γ。无人机的身份信息在蜂群起飞前进行确认,在整个作战过程中固定不变,且所有无人机个体是平等的,身份信息并不表征身份优劣,只用以区分个体身份。 在身份HA中,按照编号顺序依次为各无人机构造效率矩阵,确定打击目标。只有当邻居中位于自身编号之前无人机均已确定打击目标,无人机才开始构建自身的效率矩阵。在构造效率矩阵时,打击优势函数值采用两种设置方式:自身及自身编号之后的无人机,对敌方目标的打击优势函数值依据式(5)~式(10)设置;自身编号之前的无人机,对打击目标的优势值设置为0,对非打击目标的优势值设置为1。即在蜂群无人机的视角下,自身编号之前无人机的打击目标已确定,仅对自身以及自身编号之后无人机的打击目标进行合理分配,可以避免与自身编号之前无人机的目标选择冲突或者重复的情况发生。例如,存在无人机集合Γ={Γ1,Γ2,Γ3},打击目标集Τ={Τ1,Τ2,Τ3},无人机2号的邻居集合Λ2={Γ1,Γ3},且无人机1号已经选择对目标2号进行打击,R1={Τ2}。则无人机2号在构造效率矩阵时,将无人机1号对于目标2号的打击优势函数值设置为0,C12=0,对其他可打击但未选择打击目标的优势函数值设置为1。 在效率矩阵的基础上,需要建立统一效率矩阵来解决每架无人机可以攻击多个目标、每个目标可以被多发导弹攻击的问题[23]。当每架无人机可以攻击至多两个目标,每个目标可以至多被2发导弹攻击时,建立统一效率矩阵如图5所示。图5中,蓝色虚线矩形框表示每架无人机至多可以攻击两个目标,红色虚线框表示每个目标至多允许被2发导弹攻击。 图5 统一效率矩阵 由于蜂群无人机只能感知到周围邻居个体的信息,每架无人机的统一效率矩阵是不同的。需要为每架蜂群无人机建立统一效率矩阵,来为其决定打击目标,各自的统一效率矩阵仅决定各自的打击目标。在图5的基础上,需要对统一效率矩阵做出调整,符合以下两条规则: 1) 蜂群无人机仅可掌握周围邻居个体的情报信息,包括速度信息、位置信息、身份信息、可打击目标。蜂群无人机仅能依据掌握的情报信息建立统一效率矩阵。例如,存在无人机集合Γ={Γ1,Γ2,Γ3,Γ4},打击目标集Τ={Τ1,Τ2,Τ3,Τ4},无人机2号的邻居集合Λ2={Γ1,Γ4},则无人机2号修改后的统一效率矩阵如图6所示。 图6 掌握局部信息无人机的统一效率矩阵 2) 蜂群无人机建立统一效率矩阵时,为了尽可能避免对目标冗余打击或者避免目标遗漏,对自身编号之前无人机的打击优势函数值进行置1或者置0。例如,无人机1号已确定打击目标为R1={Τ1,Τ4},则无人机2号在建立统一效率矩阵时,n=1矩阵块无人机1号仅在m=1矩阵块设置C11=0,其余均设置为1,n=2矩阵块无人机1号仅在m=1矩阵块设置C14=0,其余均设置为1。无人机2号进一步修改后的统一效率矩阵如图7所示。 图7 身份HA中无人机的统一效率矩阵 最后采用加边补1法使效率矩阵变为方形矩阵,按照HA的求解方式进行求解,确定无人机打击目标,具体分配方法流程如图8所示。 图8 基于身份HA的无人机蜂群多目标分配方法流程 对身份HA相较于HA的优势总结如下: 1) 在HA中,无人机个体在构建统一效率矩阵时,需要对所有邻居无人机的打击优势函数值进行计算,具有一定的计算复杂度。在身份HA中,蜂群无人机在构建统一效率矩阵时,仅需对自身及自身编号之后个体的打击优势函数值进行计算,降低了计算复杂度。 2) 对于无人机蜂群,不存在控制基站向蜂群个体发送指令,且蜂群无人机通信距离有限,蜂群个体需要依据有限邻居信息进行自主判断,决定打击目标。在无人机仅掌握局部信息的情况下,采用HA可能得到对于全局糟糕的局部最优解,造成部分目标被重复打击而部分目标从未被打击,身份HA可以避免这种情况。 3) HA面向的全局信息可知的集中式分配,无法满足无人机蜂群分布式的特点。身份HA仅需无人机掌握局部信息即可,并按照身份编号依次为个体确定打击目标,完美契合蜂群无人机鱼贯依次打击的作战策略。对身份HA进行程序求解计算量是极小的,依次确认各无人机的打击目标十分迅速,不会对打击效能产生影响。 为证明身份HA适用于无人机蜂群的多目标分配问题,进行实例验证。首先对智能算法和传统算法的耗时性和稳定性进行对比;其次对拍卖算法、HA、身份HA等传统算法在全局信息可知与仅掌握局部信息两种条件下的算法性能进行对比。 张进等[23]对HA、GA、PSO算法的耗时性和稳定性进行对比,结果如图9、图10所示。本文在其成果基础上对于身份HA的耗时性和稳定性展开分析。 图9 HA、PSO算法、GA运行时间对比[23] 图10 HA、PSO算法、GA最优值对比[23] 首先对身份HA的运行时间进行分析。一方面,在身份HA中,当邻居中位于自身编号之前的无人机确定打击目标后,无人机可以确定自身打击目标,极端情况下至多需要经过N个周期确定打击目标。另一方面,身份HA仅需要无人机对自身及自身编号之后的个体的打击优势函数值进行计算,其效率矩阵的构建和求解效率均优于HA,耗时更短。因此,身份HA运行时间tIHA与HA运行时间tHA存在以下关系: tIHA (16) 以图9中20×20规模的分配问题为例,HA平均耗时为0.006 s,PSO算法平均耗时为0.830 s,GA平均耗时1.670 s。由式(16)可知,身份HA平均耗时应有tIHA<20×0.006=0.120 s,远小于PSO算法和GA。并且随着规模的上升,PSO算法和GA耗时呈指数式增长,而HA的运行时间变化不大,身份HA的运行时间和HA的运行时间呈一定线性关系,其运行时间也将远小于PSO算法和GA。 其次对身份HA的稳定性进行分析。如图10所示,在不同规模分配问题中,HA的最优值始终收敛于某一个值,十分稳定,这是因为HA是基于矩阵的操作,对于某一确定的矩阵,其求解结果也是确定的。而身份HA和HA一致,都是基于矩阵的操作,其也可以收敛至唯一的最优值,稳定性优于智能算法。 综上所述,相较于智能算法,包括身份HA在内的传统算法求解迅速且稳定,更适用于无人机蜂群实际作战。 本文提出无人机蜂群的打击效能S来评估算法性能: (17) 式中:We表示武器的有效使用数量;W表示武器的总数量;We/W称为武器利用率(例如共有4发导弹攻击了2发导弹就可以摧毁的敌方目标,则有We=2,W=4,武器利用率为50%);Ci表示无人机i对于选定的打击目标的优势函数值。 拍卖算法中,αij表示敌方目标j分配给无人机i的价值,本文中αij=1-Cij;pj表示敌方目标j的价格,在首次出价前,所有敌方目标的价格均为0。无人机i选择敌方目标j的收益记为 profitij=αij-pj (18) 每架无人机具有自利性,总是试图选择收益最高的敌方目标。无人机i试图选择敌方目标j后,对敌方目标j报价并提高其价格,敌方目标j报价有 pj_old+ε≤pj_new≤pj_old+σ+ε (19) 式中:pj_old为敌方目标j的旧价格;pj_new为敌方目标j的新价格;σ+ε表示报价增长幅度,σ为报价增长基准,ε越小,最后分配结果越优,但是会增加迭代次数,增加计算工作量。如果除了当前要提价的敌方目标j外,没有其他能够提供正收益的物品,则 σ=αij-pj (20) 如果除了敌方目标j外,还有敌方目标k,选择它产生的收益仅次于敌方目标j,则 σ=αij-pj-(αik-pk) (21) 当每架无人机都获得分配或者每架无人机试图选择敌方目标的收益都不大于0时,算法停止。 在实例中,每架无人机携带2发导弹,每一个敌方目标被2发导弹打击后,便会被彻底摧毁。本文遵循角度优势=距离优势>速度优势,设置ka=kr=0.4,kv=0.2。其他参数分别设置为Rdes=10 km,Rmax=15 km,Rmin=2 km,vC=90 km/h,vmax=120 km/h,ru=5.7 km。将敌方目标共区分为3类,具有3种不同的重要程度,则D=3。 在身份HA中,无人机仅利用局部有限信息,因此在规模上是可推广的,本文目的是验证算法的有效性和可行性,为突出本文核心重点以及减小计算量,本文以3架无人机以及3个敌方目标为例进行验证。预设存在无人机集合Γ={Γ1,Γ2,Γ3},敌方目标集合T={T1,T2,T3}。 3.2.1 信息全局可知情况下算法性能对比 信息全局可知情况下,各架蜂群无人机均掌握其他无人机的位置信息、速度信息、可打击目标信息等。设置无人机及敌方目标信息如表2所示。该种情况下,依据拍卖算法、HA和身份HA获得的无人机统一效率矩阵是一样的,每架无人机的统一效率矩阵也是一样的,建立如图11所示。 图11 信息全局可知情况下的无人机统一效率矩阵 根据拍卖算法,设置ε=0.1,各敌方目标的起拍价格均为0,无人机1号首先对各目标进行竞拍,各目标分配给无人机1号的价值分别为0.903、0.396、0.623、0.903、0.396、0.623,无人机1号选择各目标的利润分别为0.903、0.396、0.623、0.903、0.396、0.623。无人机1号最终选择敌方1号、敌方1号实施打击,并向敌方1号报价p1_new=(0.903-0.396)+0.1=0.607,敌方1号的价格修改为0.607。然后按照该步骤依次为各无人机竞拍目标。按照该步骤,无人机蜂群的目标分配结果为R1={T1,T1},R2={T3,T3},R3={T2,T2},无人机蜂群的武器利用率为100%,打击效能为S=4.172。 根据2.1节的求解步骤,由HA和身份HA得到各蜂群无人机的目标分配结果如表3所示,R1={T2,T2},R2={T1,T1},R3={T3,T3}。根据两种算法获得的分配结果是一样的,无人机蜂群的打击效果没有区别,武器利用率为100%,打击效能为S=4.268,优于拍卖算法取得的打击效能。 表3 无人机及敌方目标信息 综上,在信息全局可知情况下,HA和身份HA的性能优于拍卖算法。并且HA和身份HA性能稳定,比拍卖算法更适用于无人机蜂群实际作战。 3.2.2 信息局部可知情况下算法性能对比 信息局部可知情况下,一部分无人机之间无法进行信息交互,相互之间无法传输信息,只能依据有限的局部可知信息进行打击目标决策。设置无人机及敌方目标信息如表3所示,示意图如图12所示。通过简单计算,无人机1号的邻居集合为Λ1={Γ2},可打击目标集合为A1={T1,T2,T3};无人机2号的邻居集合为Λ2={Γ1,Γ3},可打击目标集合为A2={T1,T2,T3};无人机3号的邻居集合为Λ3={Γ2},可打击目标集合为Λ3={T2,T3}。 图12 无人机及敌方目标示意图 在该种情况下,依据拍卖算法和HA得到的各无人机的统一效率矩阵是一样的,如图13~图15所示。依据拍卖算法,得到无人机蜂群的目标分配结果为R1={T1,T1},R2={T2,T2},R3={T3,T3},武器利用率为100%,打击效能为S=4.262。 图13 依据HA无人机1号的统一效率矩阵 图14 依据HA无人机2号的统一效率矩阵 图15 依据HA无人机3号的统一效率矩阵 依据HA,由图13得到无人机1号2发导弹的打击目标分别为敌方1号、敌方1号,R1={T1,T1}。由图14得到无人机2号2发导弹的打击目标依然为敌方1号、敌方1号,造成了对目标1号的冗余攻击,R2={T1,T1}。在该种情况下,武器利用率为66.7%,打击效能为S=3.058。可见,在局部信息可知的情况下,HA无法保证无人机蜂群的整体作战效能最优。 依据身份HA,得到各无人机的统一效率矩阵如图16~图18所示。图16与图13相同,得到无人机1号2发导弹的打击目标分别为敌方1号、敌方1号,R1={T1,T1}。与图14不同,图17将无人机1号对打击目标的打击优势函数值置1或者置0,得到无人机2号2发导弹的打击目标分别为敌方2号、敌方2号,R2={T2,T2}。根据图18,得到无人机3号2发导弹的打击目标分别为敌方3号、敌方3号,R3={T3,T3}。 图16 依据身份HA无人机1号的统一效率矩阵 图17 依据身份HA无人机2号的统一效率矩阵 图18 依据身份HA无人机3号的统一效率矩阵 最终,蜂群无人机依据传统HA和身份HA的打击情况分别如图19(a)和图19(b)所示。依据HA,无人机蜂群共有4发导弹攻击1号目标,造成冗余攻击,是蜂群无人机仅掌握局部信息导致的。依据本文设计的身份HA可以避免以上情况发生,按照身份编号顺序,无人机1号首先选择打击目标,2发导弹分别攻击敌方目标1号、1号;之后,无人机2号的2发导弹选择攻击敌方目标2号、2号;最后,无人机3号的2发导弹选择攻击敌方目标3号、3号。无人机蜂群的导弹可以覆盖更多敌方目标,因此证明了本文设计的身份HA可以提升无人机蜂群整体作战效能,对于实际无人机蜂群作战具有重要指导意义,为实现无人机蜂群的鱼贯依次打击作战策略奠定基础。 在本文实例中,拍卖算法和身份HA得到了一样的分配结果,取得了最佳的无人机蜂群作战效能,是因为拍卖算法的不确定性。也是由于其不确定性,拍卖算法在局部信息可知的情况下无法保证始终能够得到最优的分配结果,并且3.2.1节中在全局信息可知的情况下,拍卖算法的性能劣于身份HA,因此相较于拍卖算法,身份HA对于无人机蜂群实际作战更具指导意义。 本文在HA的基础上添加了无人机身份信息和目标身份信息,提出了身份HA,对无人机的统一效率矩阵进行了改进,实现了无人机蜂群的分布式目标分配,避免了蜂群对敌方目标打击冗余或者遗漏打击。得出主要结论如下: 1) 身份HA能够用以指导无人机蜂群实际作战,为实现蜂群鱼贯依次打击的作战策略奠定基础。 2) 在未来,一是会扩大蜂群无人机数量规模以及敌方目标规模对身份HA进行验证,二是会对身份HA进行深入的理论分析,探求性能优于HA的边界条件,三是会对身份HA进行优化,进一步考虑无人机蜂群的动态空间构型、集群控制算法等,以实现蜂群在运动过程中仍能保证打击效能最大。2.2 身份HA

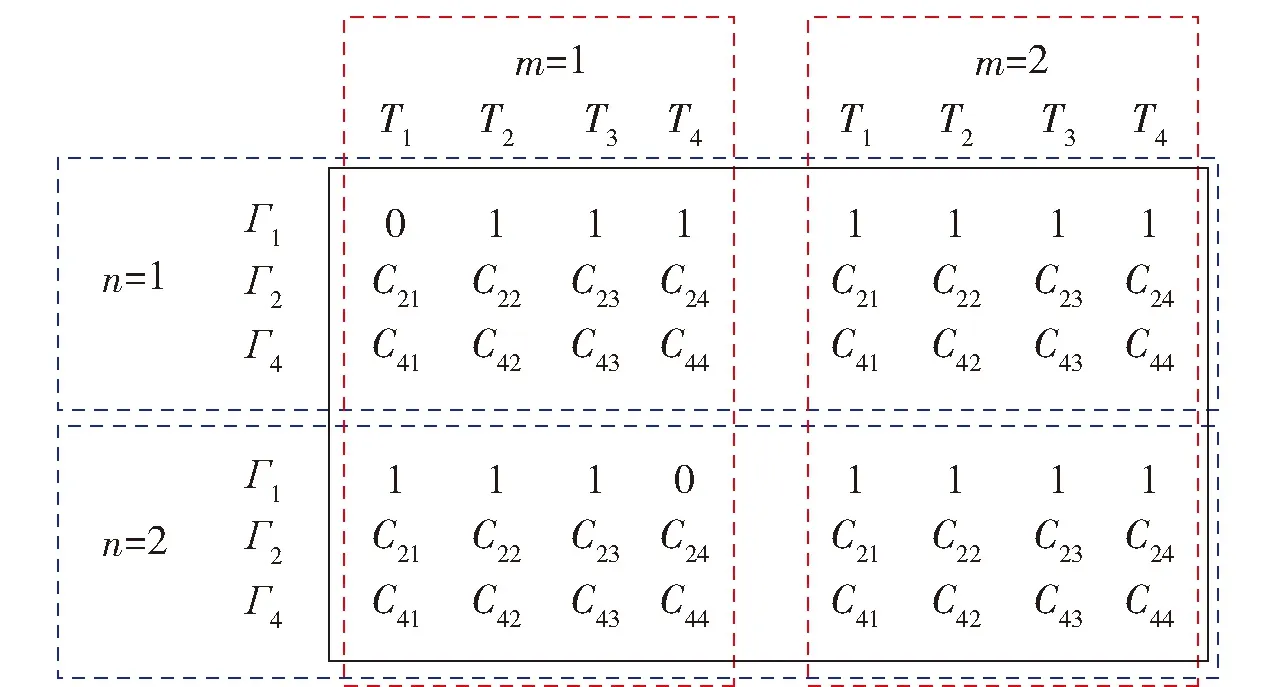
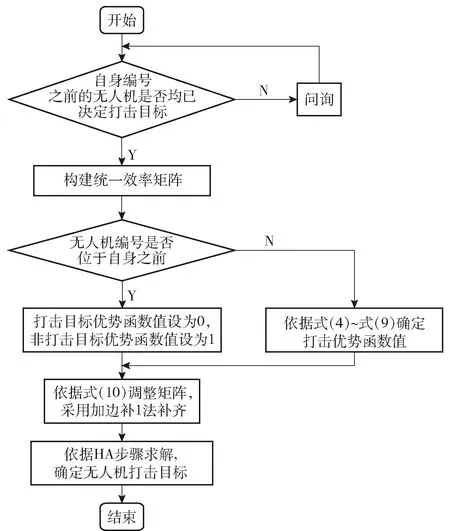
2.3 身份HA的优点
3 实验结果与分析
3.1 智能算法和传统算法对比
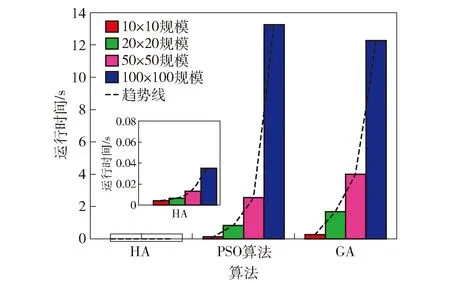

3.2 传统算法性能对比
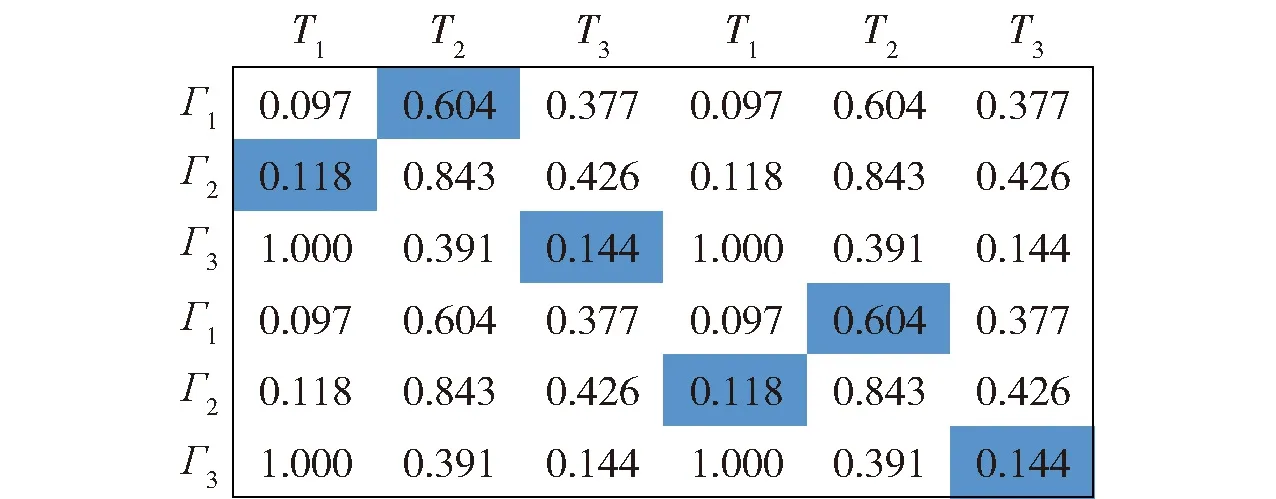

4 结论
