信息重传与丢包补偿的多无人机分布式任务分配方法

曹严, 龙腾,2, 孙景亮,2*, 周禹泽

(1.北京理工大学 宇航学院, 北京 100081; 2.北京理工大学重庆创新中心, 重庆 401120)

0 引言

随着战争形态向自主化、智能化方向演进,常规武器难以满足高精度、高动态、低成本的作战需求,无人机集群协同作战具备战场感知、态势推理、任务规划等智能化能力,具备对战场敌目标群执行高效抵近侦察、多方位自主识别及饱和打击等3D(Dull, Dirty and Dangerous)任务[1],逐步发展为现代战争的重要作战力量。任务分配技术是支撑无人机集群协同作战的关键技术之一,旨在以收益最大化为目标,综合考虑任务要求、无人机性能以及作战环境,为各机指派一定数量及类型的作战任务,避免己方资源冲突,确保无人机集群多任务的高效执行,体现集群协同的作战优势。任务分配方法通常可划分为集中式与分布式两类方法。集中式方法依靠中心节点生成任务分配方案,并向集群系统内各机分发分配结果。例如,范博洋等[2]面向协同侦打任务,研究了无人机与无人车的空地协同任务分配问题。但由于绝大多数任务分配问题的NP-hard特性,随着系统内集群规模的增加,集中式方法获得可行分配方案的求解耗时也显著增长。另外由于中心节点的存在,系统抗毁性不足。而分布式任务分配方法通过机间信息交互达成分配方案一致,系统不依赖中心节点且具有良好的可扩展性,是当前的研究热点。然而,真实战场环境下机间通信处在非理想状态,通信丢包等因素会导致分布式任务分配方法的性能降级。

当前围绕分布式任务分配已开展大量研究工作,其中基于市场竞争机制的方法是主要研究方向之一。在无人机集群典型应用场景中,单个任务的收益计算通常依赖于其他任务执行顺序,即任务间存在耦合依赖关系(ID)[3],导致分配问题具有NP-hard特性。Choi等[4]提出了一致性束算法(CBBA),用于求解包含依赖关系的单对多(SR-MT-ID)[3]任务分配问题,算法包含任务包贪心构建和冲突消解两个阶段。HIPC(Hybrid Information and Plan Consensus)[5]和PI(Performance Impact)[6]算法均采用冲突消解的方式在局部各机达成任务分配一致性共识,其中HIPC通过维护全局信息构建任务序列,而PI则是通过直接优化分配问题的目标函数来提供合理的分配方案。此外,组合优化与群智能等相关方法也是分布式任务分配领域的主要研究方向。其中DHBA(Decentralized Hungarian Based Algorithm)[7]是确定性组合优化方法匈牙利算法的分布式形式。分布式群智能方法的代表性研究则包括随机蚁群优化算法[8]和分布式遗传算法(DGA)[9]。

然而,现有文献大多采用简易模型模拟机间的通信条件。Ismail等[10]为各机在n×n任务空间内建立直径为n/2的磁盘通信模型。文献[11]使用全连通网络拓扑和一字型拓扑对比任务分配方法的性能。Zhao等[6]分别采用一字型、中心辐射型、环型和网状拓扑模拟不同的通信场景。文献[5]引入网络拓扑连通度概念评估HIPC算法的性能。陈璞等[12]面向动态任务分配问题,考虑通信距离与时间延迟等约束,设计局部一致性任务联盟分配方法。文献[13]在联盟组建中进一步考虑航迹效能因素影响,提升任务效能模型真实性。王琳蒙等[14]面向无人机空战中的信息非完备问题,从攻防博弈建模的角度设计了反向学习的改进麻雀算法,实现了纳什均衡。但上述研究并未考虑环境干扰、路径损耗导致的通信丢包影响。Otte等[15]采用Bernoulli和Gilbert-Elliot通信模型对比研究了通信丢包条件下多种典型拍卖框架的求解性能,该工作探寻了数据丢包下各典型拍卖分配架构的求解特征与规律,对后续研究工作开展具有指导意义。Han等[16]在设计无人机的控制策略时建立了信噪比(SNR)阈值模型,用以描述数据传输的质量,若SNR大于阈值则数据接收是可靠的;否则数据出现丢包。Nayak等[17]基于该丢包模型对比了5种典型分布式任务分配方法,揭示了CBBA算法在不同场景下的性能优势。Carrillo等[18]提出了一种元推理方法,使无人机集群能够根据机间通信质量自适应地选择任务分配算法。

考虑到分布式任务分配方法依赖机间通信完成分配过程,当分配问题规模上升时,机间通信负载增大。为克服该问题,文献[11]将CBBA一致性协调阶段改进为异步通信方式,减少了机间通信量。Mazdin等[19]提出了时间触发与事件触发的信息传输机制,可以有效补偿通信丢失的信息。符小卫等[20]基于运动状态估计消解通信时延下的多机任务指派冲突,当局部位置状态误差大于给定阈值时,引发间歇通信纠偏机制。文献[21]在滚动时域框架下根据机间通信距离实时切换信息交互策略,实现了通信距离受限的多机协同探测任务。CA-CBBA(Communication-Aware CBBA)[22]方法采用通信协议与分配算法协同设计的思路来处理消息冲突与带宽限制。

目前,分布式任务分配领域围绕通信丢包建模及典型算法对比开展了一定工作,但相关算法的适应性改进设计少有开展。本文面向通信丢包下分布式任务分配方法可靠设计的需求,主要开展以下工作内容:

1)提出了机间信息重传机制,并在通信丢包条件下分析了该机制对CBBA算法收敛速度提升的效果。

2)提出了丢包估计分布式任务分配(LE-DTA)算法,显著降低了机间信息重传机制导致的通信冗余,并证明了算法的收敛性,有效解决了高丢包率、低网络拓扑连通度下难以可靠、快速实现分布式任务分配的问题。

1 问题建模

本节围绕战场中多目标协同抵近侦察任务建立单对多(SR-MT)典型任务分配问题模型及机间通信丢包模型。

1.1 任务分配问题模型

定义I={1,…,Nu}为Nu架同构无人机组成的无人机集合,J={1,…,Nt}为Nt个待侦察目标构成的目标集合。单机按时序先后可对多个目标执行侦察任务,各目标仅需单架无人机抵近侦察。定义分配方案χ={p1,…,pi,…,pn},其中pi表示无人机i∈I的目标执行序列。单机的任务收益与该机目标执行序列相关,任务分配全局目标为最大化各机收益的总和,可表示为

(1)

s.t. |pi|≤Ci

(2)

(3)

(4)

1.2 通信丢包模型

考虑大尺度上无线信号路径衰落与小尺度上信号多径衰减效应,非理想通信下信噪比模型可描述为对数正态分布[25],即

(5)

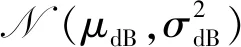
(6)

式中:Θ(i,k)=PT-PL0-10αlg(di,k/d0)-Pbar,di,k为i、k两机间的距离。定义dhop为无人机间单跳通信距离,无人机仅能与单跳内的邻机进行信息交互。dhop的计算方式如式(7)所示,当无人机间距离超过dhop时,机间数据传输丢包概率近似为1。

(7)

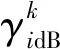
(8)

式中:符号⟹表示数据从左侧无人机可成功传输至右侧无人机,符号上方为机间传递数据包内容,⟹/则表示传输中数据包丢失。

2 机间信息重传机制

由于丢包模型中存在噪声干扰项,数据丢包是独立的随机概率事件。本文设计机间信息重传机制,以增加数据传输成功的概率,并分析信息重传对算法收敛迭代次数的影响。以无人机i为例,信息重传机制描述如下:

在任务分配过程开始前,无人机i首先与他机交互自身位置信息(或将他机位置信息提前装订),并结合式(6)依据机间位置关系计算数据传输的丢包概率P(i,k),k∈I,k≠i。任务分配过程启动后,无人机i的数据包发送机制由CBBA原算法的单次发送转变为基于丢包概率的多次发送。通常两机间预估丢包概率越大,在单轮迭代中机间所需的信息重传次数越多。为进一步阐述数据丢包对CBBA算法收敛性的影响,分析信息重传机制对算法收敛速度提升的优势,在考虑通信丢包因素的前提下,本文提出如下定理。

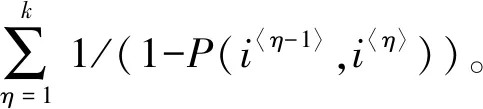
证明将信息从无人机i〈η-1〉成功传递至i〈η〉所需的迭代次数记为事件Xη,从i〈0〉传递至i〈k〉所需的迭代次数记为事件X,则X可被分解为连续发生k次事件Xη。由于事件Xη的期望为E(Xη)=1/(1-p(i〈η-1〉,i〈η〉)),则

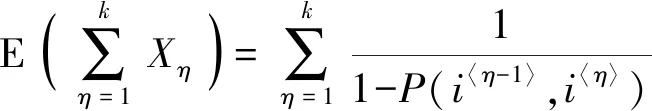
(9)

证毕。

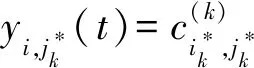
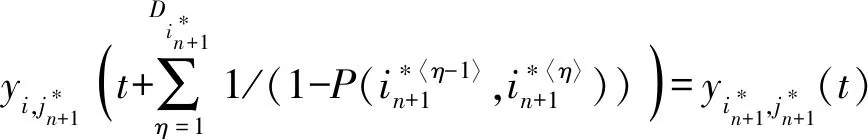
(10)

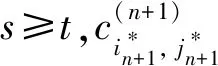
引理3在同步冲突消解框架下,若CBBA算法收益函数满足DMG条件且机间保持静态通信网络拓扑,则各机与SGA算法前n轮分配方案一致所需的迭代次数期望为

即

(11)

(12)

则对于k≤m+1,有

(13)

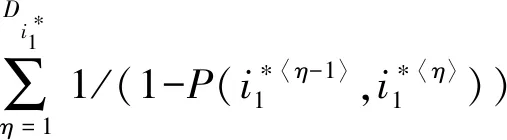
定理1在同步冲突消解框架下,若CBBA算法收益函数满足DMG条件且机间保持静态通信网络拓扑,则考虑信息重传机制下的算法收敛迭代次数Ncvg期望为

(14)

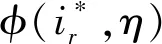
由于n的任意性,n=Nt同样成立,而Nt为算法收敛所需分配的目标数量。另外,根据文献[4]中的引理3,已生成的分配方案不会在后续迭代中更改。因此,经过

轮迭代,结合信息重传机制的CBBA算法期望达成收敛。证毕。

定理1描述了考虑信息重传后CBBA算法收敛迭代次数的期望,则标准CBBA算法在数据丢包下的收敛迭代次数期望可以看作定理1中重传次数为0的特殊情况,

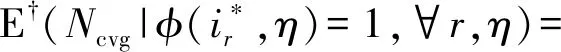
(15)

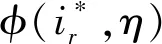
3 丢包估计分布式任务分配算法

信息重传机制可以有效降低数据丢包下CBBA算法的收敛迭代次数,但同时会带来较大机间通信负载。在确保算法快速收敛的基础上,为进一步降低机间传输信息量,本文提出丢包估计分布式任务分配(LE-DTA)算法。

3.1 算法原理及流程

LE-DTA算法用于估计CBBA算法在机间信息传输中的丢包内容。由于收益函数满足DMG条件,各机在构建任务序列时先加入的目标标书值大于后加入的目标,而冲突消解过程促使各机依据收到的最大标书值更新自身标书列表。在算法启动初始阶段,当含有最大标书值的信息传播至系统内的全部无人机时,各机形成关于最大标书值及其对应中标无人机的共识,且该分配对(最大标书值与对应中标无人机)在后续迭代过程中保持不变。注意到,虽然各机在信息交互时会将自身任务序列内全部目标及对应中标无人机信息向他机发布,但对本机更新最主要的信息为他机当前最大标书值对应的分配对。因此,若在机间通信数据丢失后本机能准确计算他机当前最大标书值及其对应中标无人机,即可将该估计信息替代丢包信息更新自身标书列表。在下一轮系统内的信息传播中,各机目标是形成次高标书值及对应中标无人机的共识,上述估计方法仍适用。此过程持续进行,直至所有目标的分配方案在全体无人机内达成一致,算法结束。

完成他机当前最大标书值解算是LE-DTA算法的核心。为实现这一功能,本机需要在本地维护三个列表:b(n)∈(J∪{∅})Nu×maxCi,∈和∈INu×Nt,分别表示各机任务包序列、各机预估标书列表及预估中标无人机列表。本机依据b(n)估算他机标书值,并利用与替代丢包数据参与冲突消解过程。无人机k在第n轮迭代中的最大标书估计值表示为其中表示无人机k的任务包序列,而根据可以求得无人机k的目标执行序列

(16)

本机预估他机标书值时,需根据当前算法迭代次数与网络拓扑结构确定被预估对象。若本机i与单跳邻机k通信出现丢包,则以无人机k为根节点,不包含子节点i的全部关联节点构成的树结构定义为i的丢包分支|→k。根据当前算法迭代次数,LE-DTA算法仅需对丢包分支内对应跳数的无人机进行预估,无需对系统内对应跳数的全部无人机进行估计,从而降低算法计算量。考虑图1中的网络拓扑结构,以1号 机为例,其单跳邻机为2号机与5号机,其余为两跳及以上邻机。1号机在每轮迭代中仅能与2号机和5号机进行信息交互。不考虑丢包影响下,在第1轮 迭代中,1号机可以获取2号机及5号机相关信息。在第2轮迭代中,1号机可以间接获取3、4、6、7号机信息。假设3号机拥有最大标书值,该信息在需要经过算法两轮迭代传递至1号机。若在第1轮迭代中出现丢包致使1号机无法获取2号机信息,则1号机应采用上述预估方法估计2号机在本轮的标书信息;若1、2号机在第2轮迭代中仍出现丢包现象,则1号机需要估计位于两跳位置的3、4号机标书值中的最大值。因此,以2号机为根节点,以3、4号机为子节点的树状结构构成丢包分支|→2。若在第3、4轮迭代中,1、5号机之间存在数据丢包,则1号机需分别预估丢包分支|→5内的三跳邻机(8、9号机)与四跳邻机(10号机)。基于上述设计思路,LE-DTA算法如图2所示。

图2 丢包估计分布式任务分配算法伪代码

LE-DTA算法的具体步骤如下:

步骤1(第1行):参数初始化。J1为算法在第1轮迭代中剩余未分配任务集合。∈为各机预估时间戳。

步骤2(第2～3行):迭代更新。处于Di跳位置的无人机相关信息经过多跳传播至无人机i后, LE-DTA算法进入新一轮迭代。

步骤4(第6～9行):预估丢包信息。对于每个丢包分支计算所有位于λ跳邻机的最大标书值并确定对应中标无人机更新该机对应的时间戳其中表示丢包分支内位于λ跳的无人机,tn表示当前时刻。

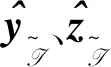
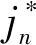
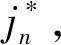
在实际应用中,LE-DTA算法可以与信息重发机制结合使用,即对于丢包概率较低的情况,采用少量信息重发即可提高信息接收概率;对丢包概率较高的情况,若信息重发后仍导致数据丢包,则采用LE-DTA算法进行估计补偿。

3.2 算法收敛性分析

本节分析LE-DTA算法收敛性,提出如下定理:

定理2在同步冲突消解框架下,若收益函数满足DMG条件且机间保持静态通信网络拓扑,则LE-DTA算法能够确保在机间信息交互存在丢包的情况下收敛,且算法收敛迭代次数上限为Nt。

LE-DTA算法理论上可以适用于任意的丢包概率。特殊地,当机间通信丢包率接近100%时(机间无通信),LE-DTA算法退化至在各机分布式运行SGA算法。

4 仿真分析

本文仿真框架采用ROS Noetic构建,由无人机和通信两类模块组成。无人机模块是独立进程,分布式任务分配算法在每个无人机模块中同步执行多次迭代,直至算法满足收敛条件。各无人机通过通信模块交换信息,并模拟传递的信息是否丢包。仿真实验的硬件环境是AMD Ryzen 7 3700X, 8-core, 3.59 GHz CPU和16 GB RAM。

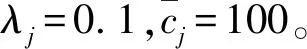
在想定Ⅱ中,任务分配问题规模增加至7机与18目标,Ci=18。通信丢包采用1.2节模型模拟,相关参数参考文献[17]设置为:PL0=40 dBm,d0=30 m,PT=30 dBm,Pbar=5 dBm,μdB=-90 dBm,σdB=7 dBm。除想定Ⅰ中对比的3种算法之外,加入HIPC[5]、PI[6]和DGA[9]等算法参与想定Ⅱ的对比工作,其中HIPC与PI算法的一致性协商阶段采用CBBA冲突消解规则[4]实现。对比分析指标包含单机最大通信传输量、算法收敛时长与目标函数值(最优性)。由于多种对比算法信息交互内容不一致,设计通信负载指标计算方式如下:

(17)

表1 各算法信息交互内容及包长

参与对比的算法最大迭代次数ζmax设置为1 000次,算法收敛条件设置如下:

{χ(ζ)=χ(ζ-τ),τ=1,2,…,2D}or{ζ≥ζmax}

(18)

式中:χ(ζ)表示算法在第ζ代的分配方案。

4.1 想定Ⅰ

考虑4种网络拓扑结构:一字型、中心辐射型、环型及全连通型,机间通信单跳距离为900 m,无人机位置如表2所示,其中代数连通度为网络拓扑对应Laplace矩阵L的次小特征值λ2(L)。

表2 不同拓扑下无人机位置(想定Ⅰ)

从拓扑连通关系上,全连通型拓扑连通度最高,其代数连通度为4,网络直径D为1,表明理想通信下各机仅需一轮迭代即可将信息传播至系统内他机;环型与中心辐射型拓扑代数连通度分别为2和1,低于全连通拓扑;一字型拓扑代数连通度约为0.59,网络直径为3,表明理想通信下某机发出的信息最多需要3轮迭代才能传播至系统内各机。考虑丢包因素,信息传播所需算法实际迭代次数高于理想通信条件。分别在多种丢包概率下开展蒙特卡洛数值仿真实验,指标统计均值如图3、图4所示。

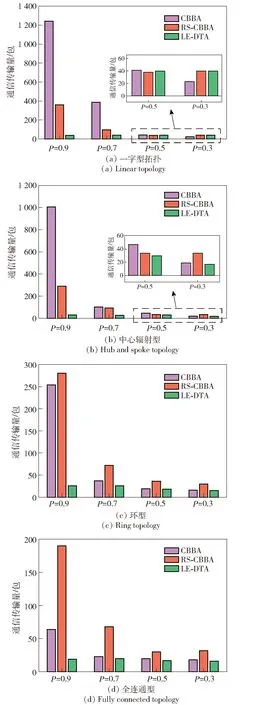
图3 通信传输量对比结果(想定Ⅰ)

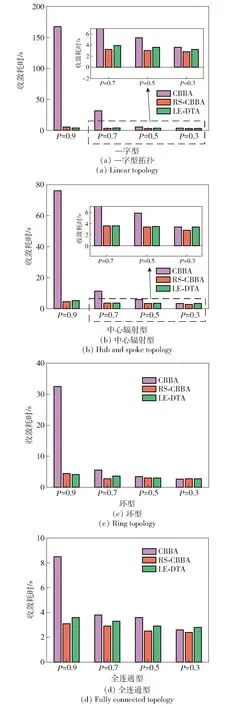
图4 收敛耗时对比结果(想定Ⅰ)

当丢包率较高(P=0.9或P=0.7)时,RS-CBBA相较于标准CBBA算法具有更快的收敛速度。表明信息重传机制可以显著降低信息丢包概率,缩短算法收敛周期。但RS-CBBA通信传输量较大,在代数连通度较高的拓扑(环型、全连通型)中,其通信传输量显著高于标准CBBA算法。LE-DTA算法在高丢包率下收敛耗时接近RS-CBBA,且具备更小的通信量。随着网络拓扑连通度的降低,LE-DTA算法的性能优势更为显著。在一字型拓扑内,当P=0.9 时,LE-DTA算法通信量较CBBA与RS-CBBA分别降低96.9%与89.2%,收敛速度较CBBA与RS-CBBA分别提升97.7%与26.4%。LE-DTA算法在P<0.9情况下收敛耗时略高于RS-CBBA,这是因为LE-DTA需要在局部维护b(n)、和列表以预估他机丢包信息,从而增加了部分计算量。另外,随丢包概率降低,RS-CBBA和LE-DTA算法在通信量和收敛速度上优势逐渐减小,这是因为两者主要围绕丢包进行改进设计,丢包出现概率越小,两者越接近标准CBBA算法。

4.2 想定Ⅱ

在想定Ⅱ中,问题规模增加至7机与18个目标,参与对比的分布式任务分配算法增加至6种(CBBA、RS-CBBA、LE-DTA、HIPC、PI与DGA)。无人机位置在([0 m, 3 000 m], [0 m, 3 000 m])的区域内随机生成。在不同路径损耗系数α下开展数值仿真实验,α越大,表明外界干扰越强,机间单跳通信距离越短,相同距离下丢包概率越高。绘制仿真对比箱线图,如图5所示。

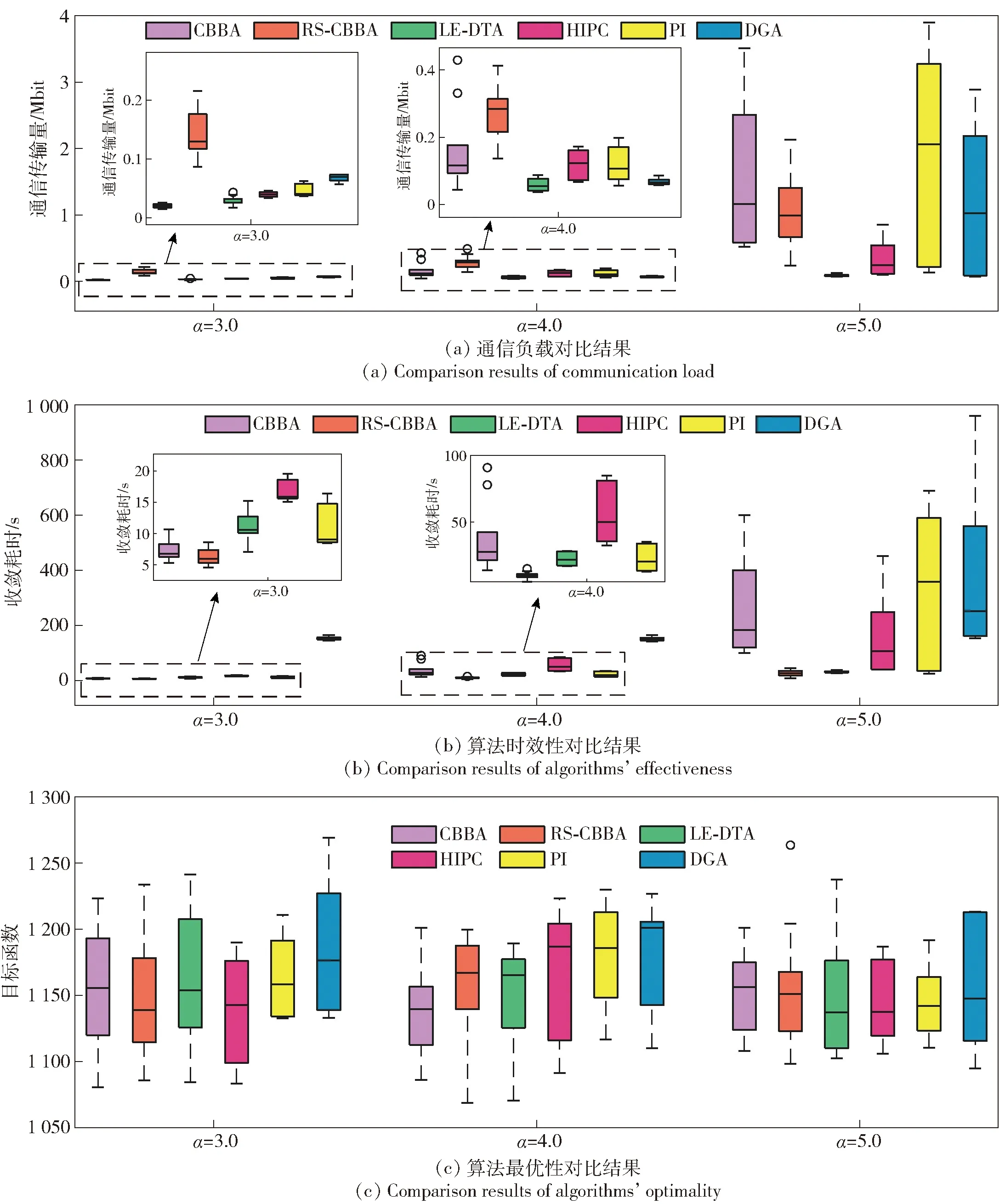
图5 算法性能对比结果(想定Ⅱ)

在通信负载方面,当外界干扰较强时,LE-DTA算法具有最小通信传输量。当α=4.0时,LE-DTA算法通信传输量均值为5.8×104bit,相对于CBBA、RS-CBBA、HIPC、PI、DGA等算法分别降低64.6%、79.9%、51.2%、50.2%、14.9%;当α=5.0时,LE-DTA算法通信传输量均值为9.1×104bit,相对于上述对比算法分别降低94.3%、91.3%、74.3%、95.2%、92.4%,表明LE-DTA算法在强干扰环境下能够节省大量通信资源,且干扰越强,LE-DTA通信负载上的优势越明显。统计α=5.0时的通信负载数据标准差,其中LE-DTA为2.0×104bit,相对于上述对比算法分别降低98.4%、96.4%、93.6%、98.8%、98.3%,表明LE-DTA算法在强干扰环境下通信负载的稳定性最优。其余算法统计数据在强干扰环境下出现较大波动的原因在于无人机位置的随机性,当某两机距离较远时机间信息丢包概率高,算法需要经过多轮迭代才能实现机间信息的有效交互。相反,当机间距离近时算法可以快速收敛。RS-CBBA算法通过增加信息重传次数提升机间信息交互成功率,机间距离的随机性同样造成较高的通信传输量标准差。而各机运行LE-DTA算法时在局部通过补偿可以有效估计丢失的传输信息。因此,LE-DTA算法通信负载在强干扰丢包环境中始终维持在较低水平。

在算法时效性方面,RS-CBBA算法具有最短的收敛耗时。当α=4.0时,RS-CBBA算法收敛耗时均值为10.1 s,相较于CBBA、LE-DTA、HIPC、PI、DGA等算法分别降低73.4%、55.5%、82.3%、55.6%、93.3%;当α=5.0时,RS-CBBA算法收敛耗时均值为27.7 s,相较于上述对比算法分别降低89.9%、12.3%、83.1%、91.7%、92.7%。结果表明,随着外界干扰的增强,RS-CBBA算法时效性优势显著。原因在于,RS-CBBA算法旨在利用机间通信资源换取更短的收敛时间。因此,在实际应用中需要在通信资源与算法耗时之间权衡。另外,RS-CBBA算法中信息重传次数的选取同样会影响算法性能,合理地选择重传次数能够有效降低冗余的通信负载。LE-DTA算法在α=5.0时收敛耗时均值与RS-CBBA算法接近,耗时标准差3.9 s低于RS-CBBA标准差11.8 s,结合通信负载指标的分析结果,表明LE-DTA算法在强干扰下具有良好的收敛性及稳定性,进一步印证了3.2节算法的收敛特性分析。

在算法最优性方面,各算法目标函数值整体接近,由于仿真实验的随机性而存在一定差异。表明针对式(1)的分布式任务分配问题,CBBA、HIPC、PI及DGA算法的求解最优性近似。另外,随着外界干扰增加,各算法求解最优性并未降低,表明针对静态分布式任务分配问题,通信丢包因素不影响算法的求解最优性,但较高的通信丢包率会显著增加算法的耗时及通信量。

注意到,当α=3.0时,LE-DTA与RS-CBBA算法较标准CBBA算法优势并不明显。这是因为路径损耗系数较低,机间形成的网络拓扑结构连通度较高,可能存在多条路径将任务信息由系统内某架机传播至另一架无人机。因此,某两机间通信发生丢包对整体信息传播影响不大。仿真结果所呈现的规律与想定I中环型或全连通拓扑类似。在α=5.0时,机间有效通信距离缩短,随机分布的无人机组成的机间通信网络拓扑连通度较低,信息传播通路减少,进而导致丢包对分布式任务分配算法收敛影响放大。此时,LE-DTA与RS-CBBA算法所呈现的性能优势与想定I中的一字型和中心辐射型拓扑仿真结果类似。

综上,在通信丢包环境下,信息重传机制可以有效提升CBBA算法收敛速度,但可能造成通信冗余。而LE-DTA算法通过估计补偿丢包信息,在确保算法收敛的前提下可以有效降低机间传输通信量。仿真结果表明,该算法在高丢包率及低网络连通度场景上具有明显的性能优势。

5 结论

本文考虑通信丢包对分布式任务分配算法影响,提出了机间信息重传机制,并分析了重传机制对CBBA算法收敛速度上的影响。为进一步降低机间通信负载,结合信息补偿提出了丢包估计分布式任务分配算法,并证明了该算法能够理论收敛至与集中式方法SGA相同的分配方案。

选取多种典型分布式任务分配算法参与对比,以通信传输量及算法收敛耗时为主要指标开展数值仿真实验。实验结果表明:信息重传机制可以有效提升CBBA在通信丢包环境下的算法收敛速度,但存在通信冗余;LE-DTA算法具备在较短时间内以更少的机间通信量获得分配方案的能力,且随着通信丢包概率的增加,机间通信网络拓扑连通度降低,LE-DTA算法的优势更为显著。

当前研究虽然在一定程度上提升了算法收敛效率,但仍难以满足实时的在线应用。后续研究将重点围绕动态场景设计分布式任务分配算法,确保在通信丢包环境下算法具备秒级及亚秒级解算能力。