基于前馈补偿的轮腿式机动平台姿态自适应控制
2023-10-07刘辉刘宝帅廖登廷韩立金崔山
刘辉, 刘宝帅, 廖登廷, 韩立金*, 崔山
(1.北京理工大学 机械与车辆学院, 北京 100081; 2.北京理工大学 前沿技术研究院(济南), 山东 济南 250300)
0 引言
轮腿式机动平台运动机构由腿和车轮组成,通过腿部关节与轮协同实现作动,具备轮式平台高机动性、腿式平台高通过性和环境适应性特性,在战场侦察、厂区巡逻、灾后救援及资源勘测等领域具有广泛的应用前景[1-3]。国内外学者在轮腿式机动平台运动控制领域开展了大量工作,如瑞士苏黎世联邦理工大学在ANYmal足式平台上开发了四轮腿平台[4]和Ascento两轮腿平台[5]、北京理工大学开发了四轮腿并联液压机器人[6]等。与腿足式机动平台不同,轮腿式平台由4个腿式结构和4个轮式结构串联组成执行机构,运动过程中需要各个驱动电机协调工作,进而实现不同的动作与任务[7]。
当轮腿式机动平台车轮滚动行驶时,可利用作动关节主动调整车身姿态角度与高度,能够执行侦察、巡逻等任务,对平台任务执行与功能拓展具有重要意义[8]。因此,国内外学者在轮腿式机动平台姿态主动控制方面开展了大量研究。Grand等[9]针对Hylos轮腿机器人,基于运动学和逆运动学模型,提出一种路径轨迹和姿态解耦控制策略。Du等[10]提出一种基于质心运动空间动量的分层控制框架,将腿式运动和轮式运动解耦,以实现不同模拟路面下的平台质心运动、腿式运动和轮式运动。刘本勇等[11]基于空间机构学位姿变换推导质心姿态与轮心位置关系,并利用非线性规划遗传算法对姿态控制过程中的质心稳定性条件进行了优化。韩子勇等[12]基于质心动力学方法和二次优化方法,通过优化车轮-地面反作用力实现了对摇臂悬挂机动平台姿态主动控制。此外,姿态控制也是腿足式机动平台的研究重点。Carlo等[13]简化了Cheetah 3四足机器人关于地面反作用力的动力学模型,利用凸优化算法求解关于地面反作用力的模型预测控制问题,提升了机器人高动态运动的稳健性和鲁棒性。张国腾等[14]建立了作用于虚拟质心的虚拟力与支撑腿关节扭矩之间的数学模型,通过调整躯干虚拟力实现了躯干高度与姿态的控制。然而,轮腿式机动平台运动过程中质心位姿与路面环境的关系是非线性并不可测的,尤其是未知环境下轮端易受到地面的冲击、碰撞、不规则地面摩擦等问题影响,极易出现作动系统“虚腿”情况,进而增大了姿态误差。
目前,开展轮腿式机动平台姿态自适应控制的关键点主要包括:1)获取轮胎与地面的接触状态,目前主流方法主要包括有触地力传感器[15]和无触地力传感器[16];2)闭环控制中获取的传感器反馈信息存在“毛刺”,需要通过状态观测器来提升反馈参数精确度。Camurri等[17]通过检测关节力矩来估计地面对机器人的作用力,实现对HyQ四足机器人的冲击检测和状态估计。在六足机器人方面,Yang等[18]采用平方根无迹卡尔曼滤波器融合处理多传感器的信息,以接触点为中心的腿部关节传感器来实现精准的状态估计,其抗噪声干扰性能比以惯性测量单元(IMU)信号为中心的状态观测器更好。Bloesch等[19]利用扩展卡尔曼滤波器设计了一种基于IMU信号的状态观测器,用以对机器人进行状态估计。Qin等[20]在双足机器人足端配置了六轴力传感器,利用足端与地面的接触面受力状态距离摩擦圆锥边界的远近来判断发生相对滑动的概率,以提升轮-地接触判别准确率。区别于腿足式机动平台,轮腿式机动平台的轮胎滚动行驶时,轮胎与地面摩擦产生的驱动力也会影响其轮端接触点受力,进而影响接触状态的判断。综上,利用单一参数难以满足轮腿式机动平台接触状态估计。
本文对轮腿式机动平台姿态控制进行解耦,建立了基于空间向量的质心动力学模型,推导了运动空间内质心位姿与轮端位置的显示数学关系。综合考虑轮端的地面反力和纵向驱动力建立了轮端接触状态估计器,结合腿部高度观测器和接触状态估计对腿部高度进行前馈补偿控制,提高轮-地接触状态估计和质心位姿控制的精确度。在轮腿式机动平台的浮动基坐标系构建整体简化模型转化为二次优化问题,实现支撑相下垂向力和纵向力的最优分配,进而获取轮腿式机动平台前馈力矩,提高平台对崎岖不平路面的适应能力。
1 轮腿式机动平台结构与组成
轮腿式机动平台主要由车身系统、感知系统、行走系统等组成,如图1所示,车身系统内部安装电池、DC、IMU、主控制器等部件;感知系统的感知控制套件Jetson Agx Xavier固定在车身内部,16线激光雷达、深度相机D435i、2个RTK天线等安装在车身表面,可实时采集行进过程中的路况信息;行走系统由4个单轮腿系统组成,采用肘-膝式布置方案,大腿由髋关节电机直接驱动,小腿由膝关节电机驱动同步带实现作动,车轮由轮边电机直接驱动,关键参数见表1。在行走系统的髋关节位置设计由摩擦片和扭簧组成的减振系统,可在一定程度上降低来自地面对行走系统的振动,满足不同路面环境下实现高效稳定运行。

表1 轮腿式机动平台关键参数

图1 轮腿式机动平台整体构型
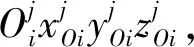

图2 轮腿式机动平台坐标系和运动空间定义

(1)
式中:qh和qk分别表示髋关节和膝关节的旋转角度。根据式(1),运动学逆解模型可以表示为
(2)
2 轮腿式机动平台质心动力学模型构建
本文建立了关于质心运动线动量和角动量的质心动力学模型。首先,通过控制质心运动实现轮腿式机动平台的姿态调节控制,其中质心空间惯量由各个子部件的空间惯量组成,即
(3)
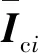
(4)

3 基于前馈补偿的姿态自适应控制策略
轮腿式机动平台在不规则障碍地形中行进时,需要保持质心姿态和高度,进而确保平台平稳运行。下面主要介绍本文提出的基于前馈补偿的姿态自适应控制策略,包括位姿状态估计、姿态高度补偿、运动规划与控制(见图3),确保轮腿式机动平台在运动空间内轮腿与地面始终平稳接触。

图3 基于前馈补偿的姿态自适应控制策略

为使平台车身始终保持一定相对位置和姿态角度行驶,质心位置与姿态角度的变化率可以表示为
(5)
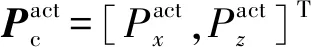

(6)
式中:Rc为质心平移时变换矩阵;P′c为初始质心位置向量;hc为质心位姿变换向量;j=1,2,3,4。在车身出现俯仰与侧倾运动时,轮端位置变换矩阵为
(7)
(8)
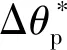
(9)
式中:R为高度变换矩阵。因此,各个轮端位置向量代入逆运动学中,即可以获得各个关节作动角度。
3.1 位姿状态估计
轮腿式机动平台配置了IMU传感器,但由于其自身精度限制、零偏误差以及其他振动、电磁等干扰的原因,导致采集的姿态角度信号中掺杂噪声干扰,给闭环控制算法中信号差分和位姿解算带来误差。为提高控制精度,本文利用拓展Kalman滤波(EKF)算法对质心姿态角度进行估计,设计了质心位姿估计的状态变量x,其表达式为
(10)
姿态角度和速度偏差的离散化微分方程可以表示为
xt+1=Ttxt+et
(11)
(12)
由于平台无横摆关节设计,本文仅考虑其纵向运动和垂向运动中的俯仰角和侧倾角。为提升估计精度,状态估计微分方程考虑了测量误差和过程随机误差均值,即
(13)
式中:wt为过程误差。基于式(11)~式(13)中给定的时序离散状态微分方程,测量方程为
Yt+1=h(xi,ζt)
(14)
式中:ζt=et+wt为测量误差与过程误差之和。因此,基于EKF算法的状态变量与观测变量的离散时序模型可以表示为
(15)

3.2 触地状态检测与车身姿态补偿策略
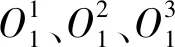

图4 左前腿坐标系定义
对于单个轮腿执行机构(见图4),其腿部和车轮运动与地面之间构成一个串并联机构,将腿部作动机构简化为杆件,平稳运行状态下的利用拉格朗日方法构建的动力学模型可以表示为
(16)
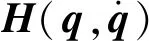
(17)
式中:PO1、PO2和PO3分别为大腿、小腿和车轮的质心位置坐标,如图4所示。对位置坐标进行微分可求得各坐标原点的运动速度,可获取各个杆件与车轮的动能Ek和势能Ep,可得拉格朗日函数为
L=Ek1+Ek2+Ek3-Ep1-Ep2-Ep3
(18)
联立式(16)~式(18),考虑小腿端部外力f∈R3×1,可得拉格朗日方程中的各系数矩阵为
(19)
(20)
(21)
G=[G1,G2,G3]T
(22)
(23)
式中:m2为表示小腿质量;I3为轮端旋转惯量;l=m2L1L2mκ=(0.5m1+0.5m2+m3)gL1,m3为轮端电机和轮胎质量;mν=(0.5m2+m3)gL2;qhk=qh-qk。
根据式(19)、式(23),f∈R3×1可以表示为
(24)
式中:f=[fx,fy,fz]T;τ*为关节和驱动轮力矩。根据式(24),可以获取轮腿式机动平台小腿端部与轮腿轴心的垂向支撑力fz。与足式平台不同,轮腿式机动平台通过带驱动电机的轮腿与地面实现接触,轮边驱动电机产生驱动力矩τw,进而产生纵向驱动力fxw克服与行进速度相反方向的纵向摩擦力实现期望运动,即
(25)
式中:Rw表示轮胎半径。本文仅考虑平台纵向和垂向运动,轮端受力可以表示为
(26)
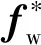
(27)
(28)

(29)
根据分析,本文设定阈值σm判断轮腿式机动平台中轮胎与地面接触状态,即
(30)
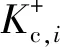
根据分析,获取当前各个腿部高度对控制器高度补偿具有重要作用。因此,根据平台腿部作动系统反馈实时角度位置关系,建立平台各个腿部高度值观测器,如式(31)所示:
(31)
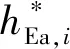

图5 车身姿态实时补偿算法
3.3 运动控制策略
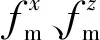

图6 轮腿式机动平台整体质心虚拟模型
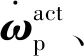
(32)

(33)
式中:I∈R2×2为单位矩阵;pi×∈R2×2表示各个腿部作动机构相对于质心的位置坐标;fm、τm分别为作用于机身质心的广义力和广义力矩。基于式(33),质心虚拟力分配任务可以转化为二次规划问题,即
min (Af-b)TS(Af-b)+αfTWf
s.t.Cf≤dm
(34)
根据上文对轮-地接触稳定分析,在开展各腿部作动机构虚拟力分配时需要考虑其所需虚拟力的取值范围,不仅可使轮端与地面实现稳定接触,亦可确保各关节和轮边驱动电机稳定可靠输出,即
(35)
式中:f*,min和f*,max分别表示不同方向分配虚拟力的最小值和最大值;μ为轮胎与接触路面的静摩擦系数,不等式矩阵Cf≤dm可以表示为
(36)

基于二次规划算法求得的各个腿部作动机构的虚拟力分配结果,结合运动学和力平衡分析求得的雅克比矩阵,得到作用至关节电机的驱动力矩,该力矩作为驱动关节的前馈力矩,其表达式如下:
(37)
(38)
利用PD控制算法可以求得反馈力矩,即
(39)
4 仿真分析
本文利用数学仿真软件建立了轮腿式无人机动平台多刚体模型,根据设计构型和传感器配置调用模型库进行参数设置,模拟车身中配置的IMU获取质心侧倾、俯仰和横摆姿态角度和角速度,组合导航获取车身实时位置和速度,关节连接模块获取关节角度、角速度和驱动力矩等参数。为验证所提出的控制算法,本文建立了一个由双边桥、波形障碍及侧坡组成的路面环境,如图7所示。在仿真过程中,设定期望运动轨迹,其中在起步阶段0~1 s时平台纵向速度从0 m/s加速至0.3 m/s,然后平台以期望俯仰角为0°、侧倾角为0°、质心高530 mm、纵向速度为0.3 m/s的速度匀速前进通过障碍。
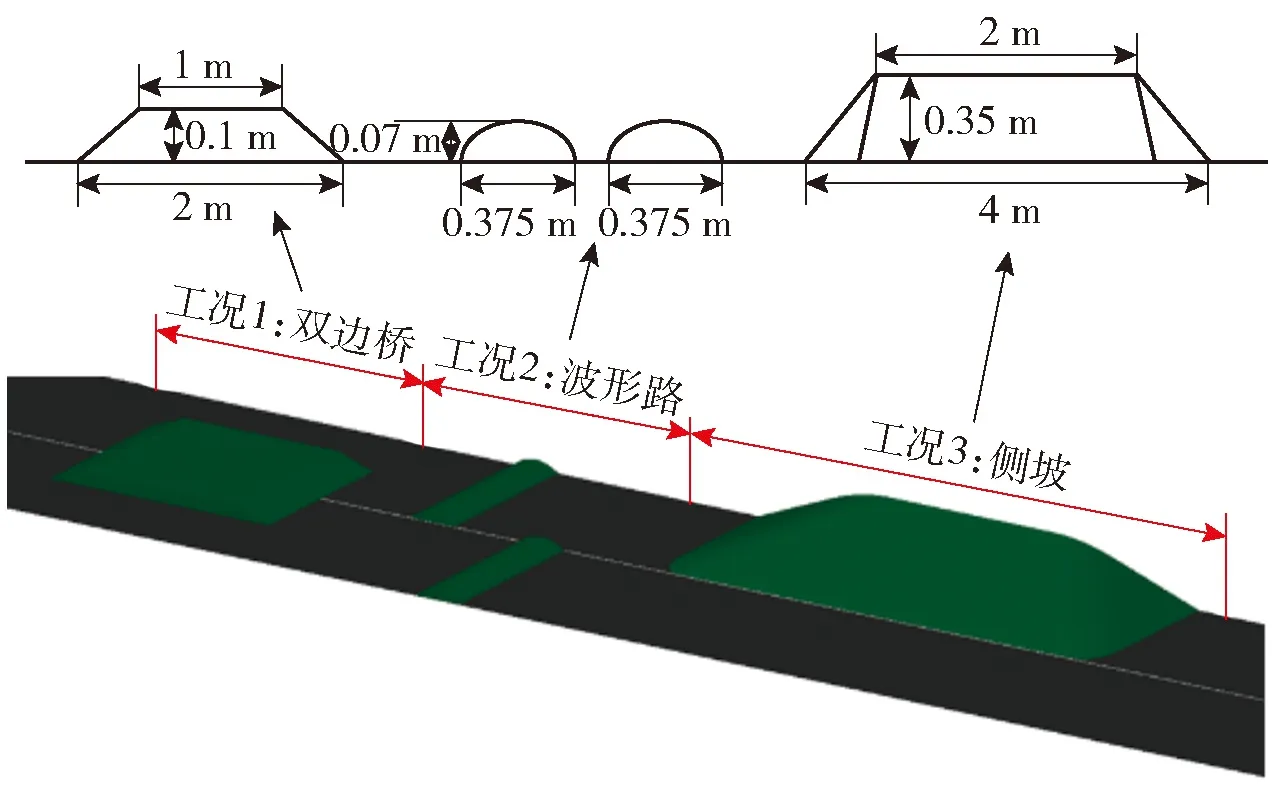
图7 轮腿式机动平台运行及工况示意图
图8为在不同障碍场景下的轮腿式机动平台的姿态自适应仿真效果,首先在t=0 s时仿真开始,然后在t=4 s时进入第①阶段的双边桥障碍,在本阶段中机身姿态角度和高度始终与初始状态一致,通过第①阶段后进入两个波形障碍的第②阶段,在本阶段中仅有一个车轮越过波形障碍,其余车轮均在平直路面,验证平台在短波形障碍下机身姿态调整水平。此外,采用侧坡工况验证轮腿式机动平台侧倾姿态控制效果,轮腿式机动平台在第③阶段中为左侧车轮开始上侧坡,等左侧前后两个车轮都上坡后进入第④阶段,此时右侧两个车轮在水平路面上,左侧两个车轮在侧坡障碍行驶,通过调整左右侧腿部高度,实现姿态角度和机身质心高度始终保持与初始状态保持一致,然后在图8中第⑤阶段左侧车轮依次离开侧坡,两侧车轮均进入水平路面。
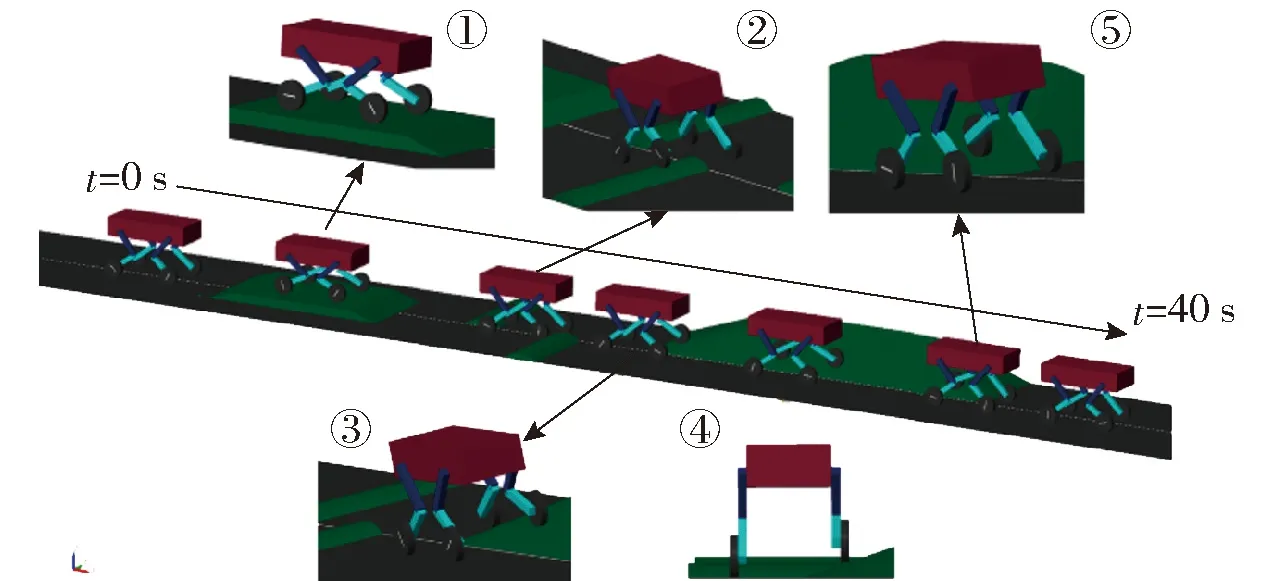
图8 轮腿式机动平台仿真运动过程
图9(a)和图9(b)为轮腿式机动平台车身质心姿态角度仿真效果,平台在第4.4 s开始接近障碍,在第37.2 s时平台左后轮离开障碍。从图9中可以看出,实际俯仰角和侧倾角的最大跟踪误差分别为-0.862°和0.369°,平均误差分别为-0.276°和 0.102°。图9中,通过对比姿态角度的实际值与估计值,其俯仰角与侧倾角估计值最大误差为0.014°和0.009°,平均误差值分别为-0.005°和 0.001°。

图9 车身质心姿态角度结果
图10和图11为轮腿式机动平台纵向与垂向的速度与位置的跟踪仿真结果。由图10可以看出,轮腿式机动平台质心的期望纵向速度为0.3 m/s,实际行驶速度会在越障过程中出现波动,纵向跟踪终止位置为11 754 mm,与期望最终位置为11 850 mm,最终跟踪误差96 mm。从图11中可以看出,轮腿式机动平台垂向位置的最大跟踪误差为5 mm,平均跟踪误差为-2 mm。图12(a)和图12(b)分别表示在该工况下左前腿和右前腿的各个关节运行角度和力矩结果。在行驶过程中,轮腿式机动平台关节力矩作动平缓,关节力矩最大值<60 N·m,满足关节力矩阈值约束。
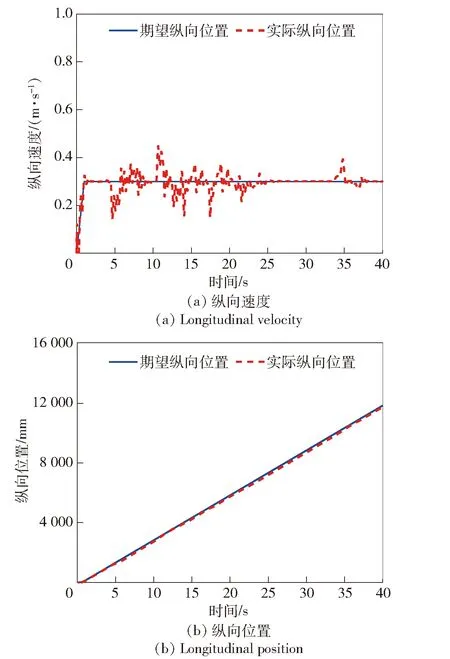
图10 平台质心纵向速度与位置仿真结果
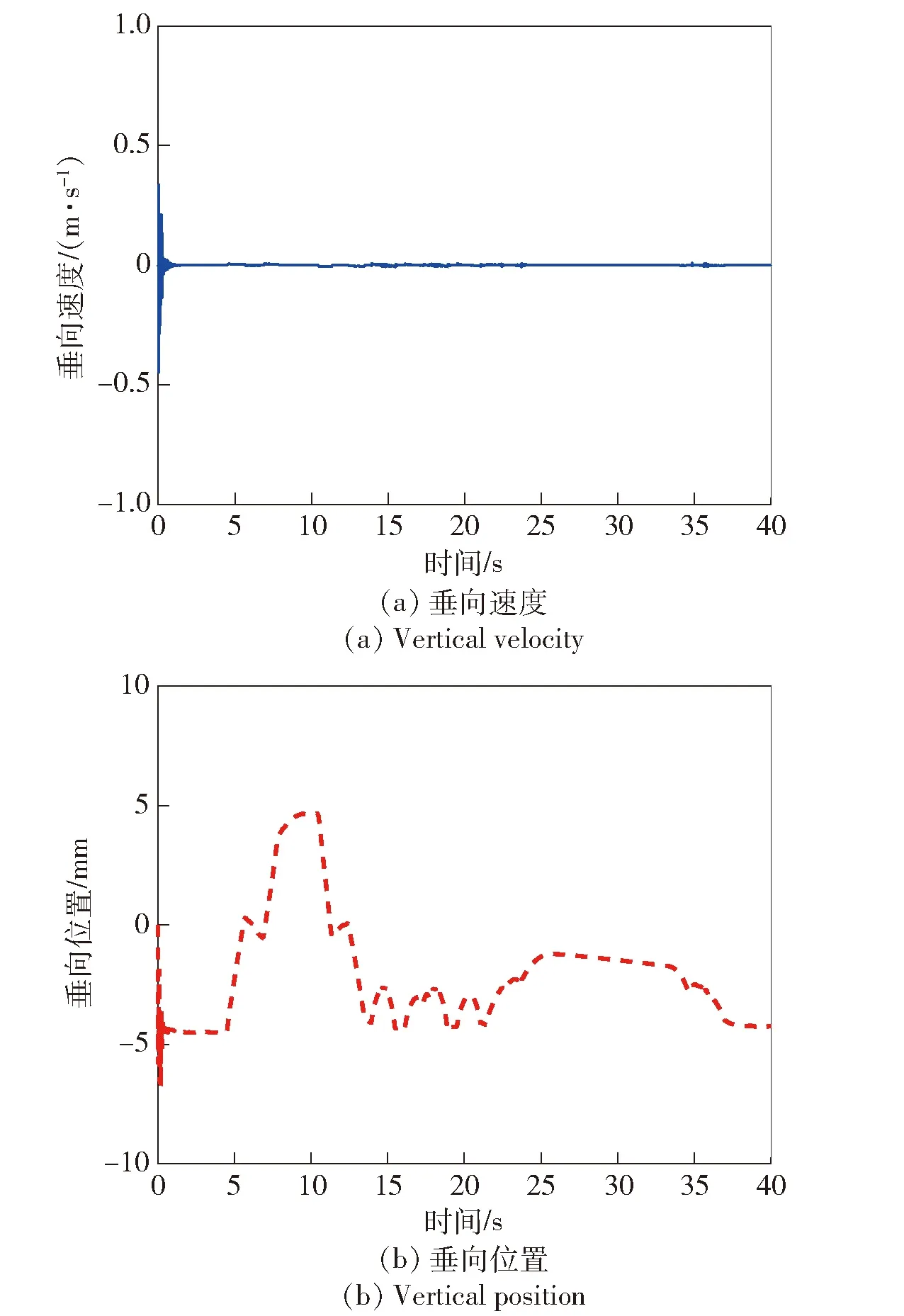
图11 平台质心垂向速度与位置仿真结果

图12 轮腿式机动平台左/右前腿关节运动角度与力矩结果
图13(a)、图13(b)分别为不同腿部作动机构下轮-地接触检测指令结果,经统计,无前馈补偿下不同轮腿作动系统中轮-地接触指令为0情况占比分别为0%、5.717%、2.632%和5.080%,而带有前馈补偿下指令0情况占比0%、4.380%、2.790%和4.367%。对比可知,带有前馈补偿策略可以明显降低轮-地接触为0的概率。
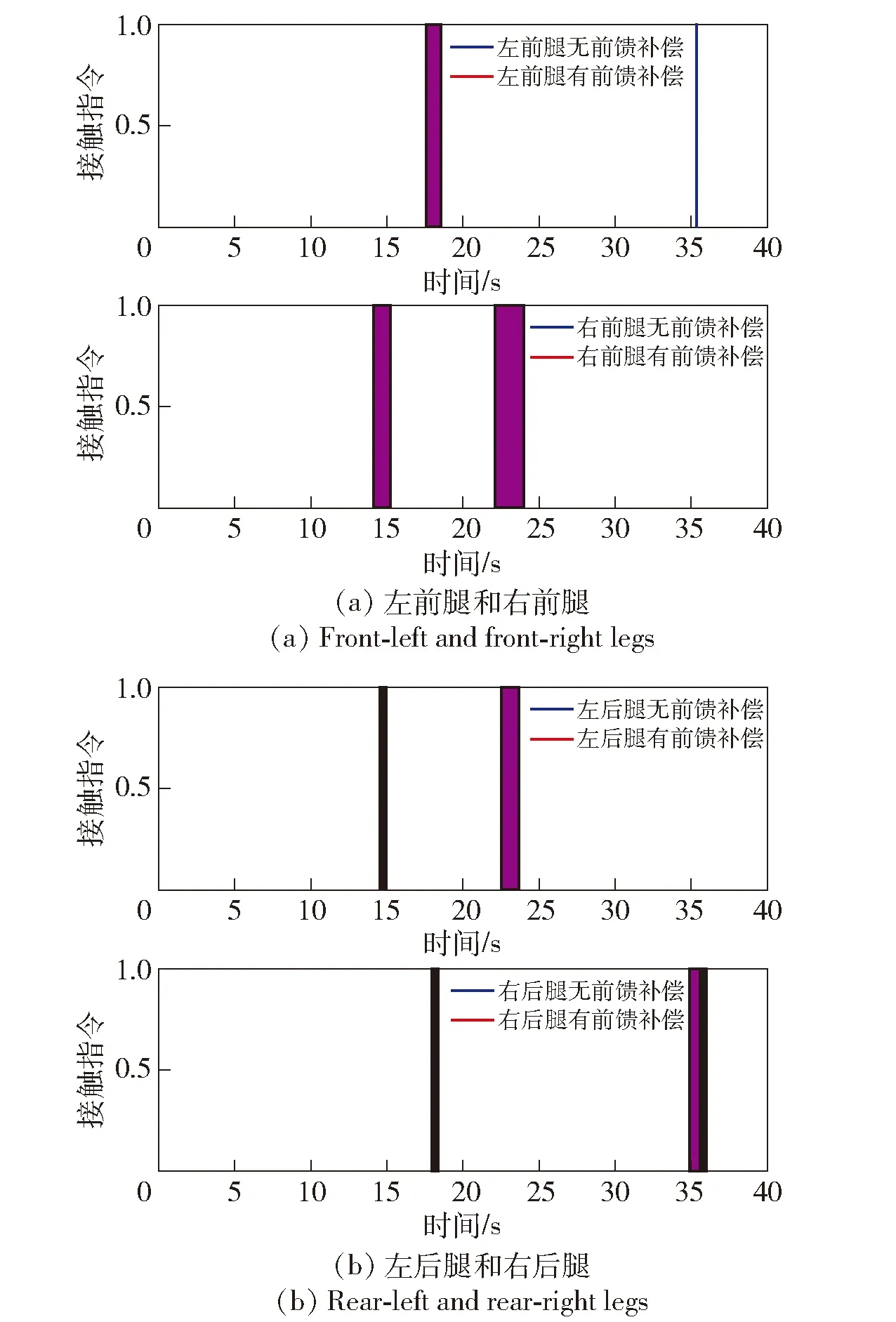
图13 轮腿作动机构的轮-地接触指令结果对比
通过Simscape模型中的接触工具箱模型,获取了车轮与地面的垂向支撑力,如图14所示,对比了带有前馈补偿策略和不带前馈补偿策略下的轮-地接触力。表2对比了两种策略对俯仰角和侧倾角的影响情况,其中所提出的控制算法对俯仰姿态精度具有明显的改善。与地面处于不稳定接触状态时,车轮具有离地腾空的趋势。所提出的前馈补偿策略提高了车轮与地面的垂向支撑力,提升了与地面的接触概率,可有效降低作动过程中不稳定接触的情况,提升其行驶过程中驱动轮的稳定性,同时有效提升了其姿态保持的控制效果与精度。

表2 仿真结果对比
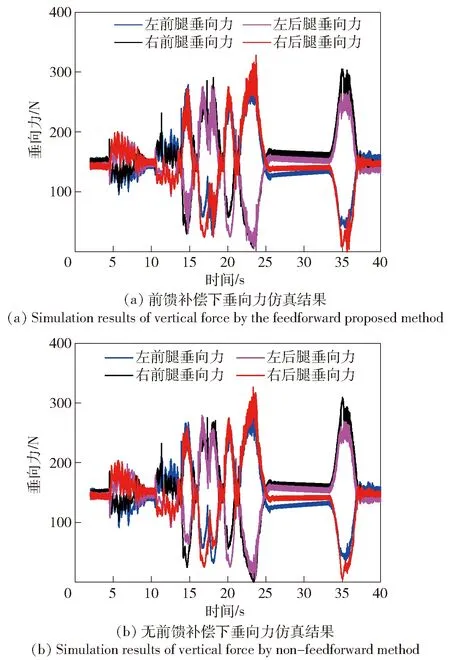
图14 轮腿式机动平台轮-地接触力仿真实验结果
仿真在CPU Inter Corei7-10750H 2.6 GHz、RAM 16G的笔记本电脑上进行。本文统计了所提出算法中耗时最长的二次规划算法,如图15所示,其中计算耗时最长为0.872 ms,平均耗时为0.225 ms,这就表明所提出的算法具备应用于实时控制的潜力。
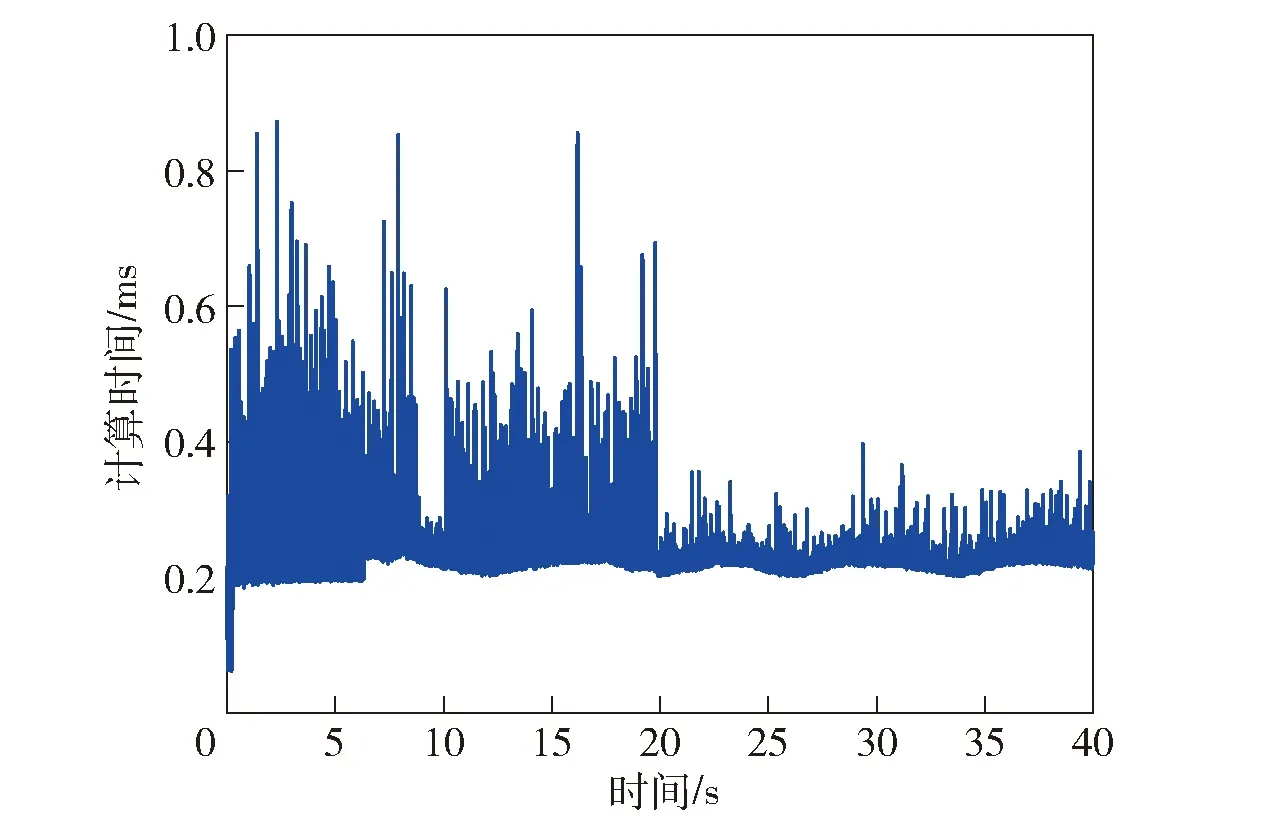
图15 二次规划算法求解时间
5 结论
本文以轮腿式机动平台为研究对象,针对复杂路面下姿态控制精度与轮-地接触力分配的问题,研究了机身姿态自适应控制算法。得出主要结论如下:
1) 分析了轮胎与地面接触时轮-地接触点摩擦约束条件,在考虑轮端垂向支撑力和纵向驱动力的基础上构建了触地状态估计器。
2) 结合高度估计器对运动状态下轮腿平台腿部高度进行前馈补偿。为轮腿机动平台在非结构路面环境下姿态自适应控制的精确性和平稳性提供基本依据和支撑。
3) 为验证所提出方法的可行性与有效性,利用数学仿真软件进行仿真,对比了无前馈补偿策略和带前馈补偿的机身姿态自适应控制策略,仿真结果符合预期。
4)在未来工作重点中,将对轮腿式机动平台在未知全地形环境下的鲁棒控制开展研究,进一步考虑抑制多源未知干扰信息对运动控制算法的影响。
