基于序列生成对抗网络的无人机集群任务分配方法

2023-10-07严钰文毕文豪张安张百川

兵工学报 2023年9期

严钰文, 毕文豪, 张安, 张百川

(西北工业大学航空学院, 陕西西安 710072)

0 引言

在强对抗、高动态、深度不确定的现代复杂战场环境下,仅靠单架无人机有限的飞行和载荷能力很难独自完成战场态势的区域监视、多目标攻击等任务。通过大规模、低成本的异构无人机平台相互协调配合组成的无人机集群,能够突破单架无人机探测能力、武器载荷等限制,在复杂环境下进行协同搜索、协同干扰、协同攻击、协同察/打、集群对抗等行动,进而更大程度地提升作战效能。

无人机集群作战带来的巨大规模优势和作战效能引起了以美国为代表的世界各军事强国对无人机集群作战技术的热切关注[1]。其中无人机集群任务分配技术作为无人机集群作战的关键技术之一,能够在满足各项战术和技术指标的前提下将任务合理、高效地分配给相应的无人机,让有限的作战资源发挥最大的作战效能,是实现无人机集群化、自主化和智能化的重要手段[2]。深入研究无人机集群任务分配技术,挖掘更有效的任务分配方法,对提升无人机集群高效遂行任务能力、推动国防力量的建设具有重要的意义,已成为各国防工业部门、科研机构的研究热点。

目前研究中,通常是将任务分配抽象成组合优化问题,在特定的场景下对问题进行一定简化后建立多约束模型[3-5],并使用任务分配算法进行求解。在求解任务分配问题时,为了降低算法求解难度、提高求解质量与求解速度,国内外学者开展了深入研究[6],并根据求解思路的不同将求解算法分为集中式算法和分布式算法两类。

集中式算法可进一步分为最优化方法和启发式方法。随着任务分配问题的复杂化,以动态规划、分支定界等[7]为代表的最优化方法不能充分反映战场环境的复杂性,对战场环境随机性和动态性的表达也极为困难,因此近年来该类型的算法研究逐渐减少[8]。启发式方法在求解多无人机任务分配问题时易于实现、性能优越,在任务分配问题中得到广泛运用。其中典型的启发式算法包括蚁群算法[9]、粒子群优化(PSO)算法[10]、模拟退火算法[11]等。在使用启发式算法求解任务分配问题的研究中,通过改变算法的编码方式和启发函数来提升求解性能,是目前研究的主要方向之一。文献[12]对无人机协同多任务分配问题进行研究,将分工机制应用于蚁群算法,并设定了基于任务代价的状态转移规则,有效地提高了算法的优化能力与求解效率。文献[13]将密度值最大聚类和混合PSO算法相结合,实现了对空地协同系统的任务分配,能够处理较大规模的任务分配问题。文献[14]研究了多类型无人机编队并建立了无人机集群网络拓扑结构,针对不同的网络拓扑结构,采用PSO算法进行任务分配问题的求解。文献[15]通过在PSO算法的个体更新环节加入引力搜索机制,提高了算法的收敛速度,并将其应用于多无人机协同侦察任务分配问题求解。然而,上述算法由于本质上的随机性,在搜索过程中会产生大量无用的劣质解,当面临大规模任务分配时其搜索效率不高。

分布式算法采用分布决策的思想,将各无人机作为独立的智能体,通过各无人机之间的协商与决策来获得最终任务分配方案。该类算法具有时效性好、鲁棒性强的优点,因此多用于注重时效性的任务分配问题中[16]。文献[17]提出了一种扩展合同网协议,能够在处理任务之间时间约束的同时保证各无人作战飞机之间的协调配合。文献[18]在应用合同网协议算法解决实时任务分配问题时引入并发机制,同时将招标者作为基准来筛选优质的投标者,提高了协商效率,减少了通信量和通信频次。文献[19]提出一种分布式鲁棒拍卖算法,在拍卖过程中引入任务奖励反馈机制,有效地降低了任务分配系统的成本,并提高了任务分配应对复杂环境的能力。然而,当任务分配问题规模较大时,会导致无人机之间协商通信量大大增加,降低问题求解效率。

上述两类算法在针对小规模多无人机任务分配问题时能在较短时间获得较好的求解质量。随着异构无人机类型的逐渐增加、无人机集群规模不断扩大,问题的约束条件将变得复杂耦合,上述算法的求解效率将不断降低,不能满足复杂战场情况下多约束大规模异构无人机集群任务分配问题对求解的实时性要求。

人工智能理论在近年来不断完善和发展,引起了研究者的广泛关注[20],也为多无人机任务分配问题的求解提供了新的思路。早期利用神经网络对无人机集群进行聚类分组等处理后与启发式算法结合,能够保证任务分配之后无人机集群的协同性[21]。近期研究中使用神经网络直接实现端到端的任务分配方法,如基于强化学习和注意力机制的任务分配方法[22]。该类方法将任务分配问题抽象为组合优化问题后,采用深度强化学习网络模型学习最优的决策策略,能够在离散决策空间中寻找到最优决策组合,并通过多头注意力机制等方法提高求解质量[23]。由于无人机集群任务分配问题同样在建模时可以抽象为组合优化问题,利用深度强化学习来实现无人机集群任务的分配研究逐渐增加。但当前研究中利用深度强化学习网络解决单目标优化问题比较成熟,对于多目标优化的相关研究还在开展中。在深度学习的网络结构中,生成对抗网络(GAN)[24]作为一种生成模型,与以往生成模型相比,其设计自由灵活,不限制生成数据的维度,且理论上能够逼近任意函数,在处理复杂数据信息时具有优越的性能,能为无人机集群任务分配问题的高效求解提供可能性。GAN在图像生成、语音合成、风格迁移等领域[25-27]取得了较好的应用效果,其网络结构的创新和优化是其不断发展的重要原因[28]。2014年提出的条件生成对抗网络(CGAN)[29]为GAN增加了显式的外部信息以指导样本生成。Radford等[30]将卷积神经网络(CNN)引入GAN架构中,显著提高了网络的表征能力。除了在网络结构上对GAN进行改进以外,对loss的优化[31]和梯度更新策略的设计[32]增强了GAN模型的生成能力,为GAN的衍生模型在众多领域的应用提供了支持。文献[33]使用基于GAN的数据-机理混合驱动方法进行子能源模型的参数辨识,实现了较高精度的辨识效果,解决了不同工况下的模型切换问题。文献[34]结合GAN提出了一种水声目标识别模型,与传统方法相比具有更强的鲁棒性。文献[35]在原始GAN结构上增加了用于回归预测的回归模型,有效提高了原油总氢物性的回归预测精度及稳定性。文献[36]对GAN在作战体系研究领域的应用进行了分析展望,指出当前GAN的衍生模型对作战场景下的相关研究问题有较强的借鉴意义。

本文结合GAN与无人机集群任务分配模型,针对传统分配算法求解效率低下、无法适用于大规模无人机集群任务分配场景的问题,提出一种基于任务分配序列生成对抗网络模型(TA-SeqGAN)的任务分配方法,该方法的创新点如下:

1)提出基于CNN与门控循环单元(GRU)的生成模型,构建战场信息矩阵,建立战场信息到任务分配序列的映射关系,有效地提取了战场信息特征并使其能够指导任务分配序列的生成。

2)提出基于多层CNN的判别模型,利用不同大小的卷积核对输入数据矩阵进行卷积操作,更有效地判别任务序列之间的相关性。

3)针对任务分配序列的离散性导致的网络无法进行梯度更新的问题,提出收益-评价双指导式生成模型梯度更新方法,并将任务分配收益模型引入策略梯度的动作值函数中,提高了生成任务分配序列的质量和生成序列的合理性。

本文首先对无人机集群任务分配问题进行描述,然后介绍基于TA-SeqGAN模型的无人机集群任务分配方法,接着设计仿真实验验证算法的有效性,最后进行总结和展望。

1 无人机集群任务分配问题

1.1 问题假设

为方便后续研究,首先对无人机集群任务分配问题做如下假设,并给出任务分配问题的相关约束:

1)在观察、调整、决策以及行动(OODA)环中,侦察和打击是其中的重要环节,故针对无人机执行侦察和打击两种任务进行研究;

2)参与分配的N架无人机具有不同功能和类型,同时能够满足完成待执行的M个任务的需求;

3)考虑各无人机以相同且恒定的速度飞行,并忽略无人机起降时的消耗;

4)无人机的位置、无人机自身性能、任务点位置、任务需求信息为已知;

5)根据已有研究文献的仿真实验和美军实际作战试验,将待执行任务无人机数量和任务数量均大于30认定为较大规模任务分配场景。

1.2 问题描述

在任务分配过程中,给定分配的无人机序列U={U1,U2,…,Ui,…,UN}和待执行任务序列T={T1,T2,…,Tj,…,TM},任务分配方案可表示为M=∪i∈1:N,j∈1:M{(Ui,Tj)},其中{(Ui,Tj)}表示无人机Ui执行任务Tj。最终需要求取任务分配收益函数R(Ui,Tj)最大时所对应的无人机集群任务分配方案,目标函数如下:

(1)

式中:Ja为无人机执行打击任务的攻击收益函数;Jr为无人机执行侦察任务的侦察收益函数;Jd为无人机执行任务的路径损耗函数。针对无人机集群任务分配问题的约束描述如下:

(2)

(3)

(4)

2 基于TA-SeqGAN模型的无人机集群任务分配方法

GAN设计了一种新的网络模型框架,包括生成模型G和判别模型D两部分。生成的对抗网络结构如图1所示。

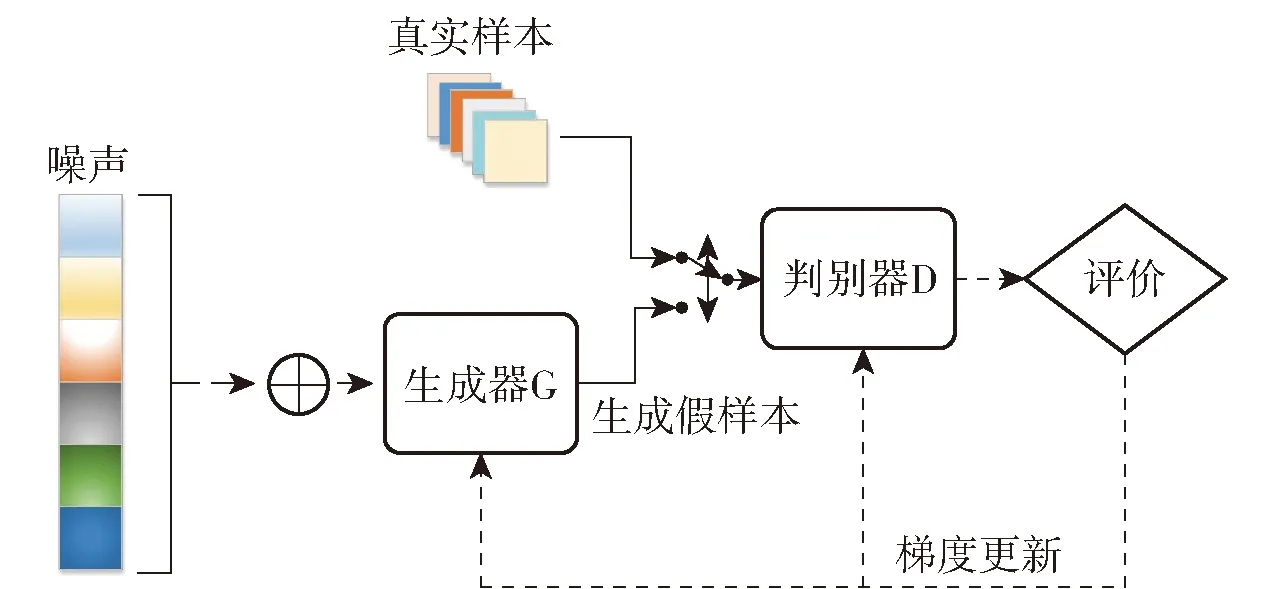
图1 GAN模型结构

图1中,生成模型G用于捕获真实样本的概率分布,学习如何产生真实的样本来“欺骗”判别模型;判别模型D用于区分真实样本和虚假样本(即生成模型生成的样本)。

G和D采用对抗博弈的训练方式,当D无法区分真实数据和生成数据时,网络便达到了理想状态。本质上,GAN的学习过程实际上是极大极小化目标函数,如式(3)所示:

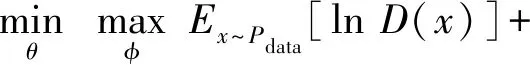
(5)

式中:θ为生成模型参数;φ为判别模型参数;Pdata表示真实样本的概率分布;Pz表示噪声的概率分布;Ex～Pdata、Ex～Pz分别表示从真实样本和噪声中采样数据后进行期望计算;D(x)为数据x经过判别模型后的输出;D(G(z))为生成模型产生的结果G(z)经过判别模型后的输出。训练过程中先固定G、优化D,使得式(5)最大化后,再固定D、优化G,使得式(5)最小化。不断重复上述过程,直至达到预定目标。

TA-SeqGAN在上述GAN模型的基础上进行改进,使得模型能够以特定的战场信息矩阵作为输入条件约束,利用网络提取输入信息矩阵的特征并生成与给定信息矩阵一致的任务分配序列。下面分别建立生成模型和判别模型。

2.1 基于CNN和GRU的生成模型建立

TA-SeqGAN中的生成模型使用序列生成模型,利用神经网络实现战场信息数据到模型数据的映射,充分提取战场信息所包含的特征,并使其能用于指导分配序列的生成。因此TA-SeqGAN的生成模型包括一个用于处理战场信息的特征提取网络,以及根据特征生成任务分配序列的序列生成网络。

2.1.1 基于CNN的战场信息特征提取网络

影响最终分配结果的因素往往包括无人机自身性能、任务收益、路程消耗等,由此可以将战场信息分为位置信息和资源信息两类。

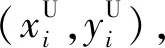
(6)

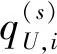
(7)

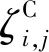
生成模型的战场信息特征提取网络核心采用CNN[37]搭建。卷积网络是一种多层监督学习网络,目前已知该网络在进行特征提取方面有着较为成熟的理论和实践经验。其核心是利用一个卷积核对原数据进行卷积操作,得到一个新的特征矩阵,A为卷积核,B为原数据,C为卷积后的数据。所谓卷积,即卷积核与原数据中对应大小的子矩阵进行各对应位的相乘计算,如图2(a)所示。Γ表示大小为3×N×M的战场信息矩阵,其包含了地图位置信息与资源信息,如图2(b)所示。

图2 卷积操作与输入战场信息矩阵

以战场信息矩阵Γ作为CNN输入,首先通过卷积和池化操作得到输出高维特征矩阵ΓCNN,这里使用了自适应池化使得不同大小矩阵在经过池化后的大小统一。随后对其展平成一维向量,再通过全连接神经网络进行特征降维处理,得到战场信息特征1×Lh的向量Ih,Lh为可变网络超参数,完整的战场信息特征提取网络如图3所示。

图3 战场信息特征提取网络结构

2.1.2 基于GRU的序列生成网络

TA-SeqGAN中用于生成任务分配序列的网络采用GRU[38]进行搭建。GRU是循环神经网络(RNN)[39]的一种变体,能够记录过去的生成信息并充分利用该信息进行当前序列值的生成。GRU与RNN相比,在单元内部增加了两种门控运算——重置门控运算和更新门控运算,使得在较长序列生成时网络能够选择性地对信息进行记忆和遗忘,同时又能在一定程度上保证运算速度。

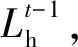
(8)

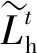
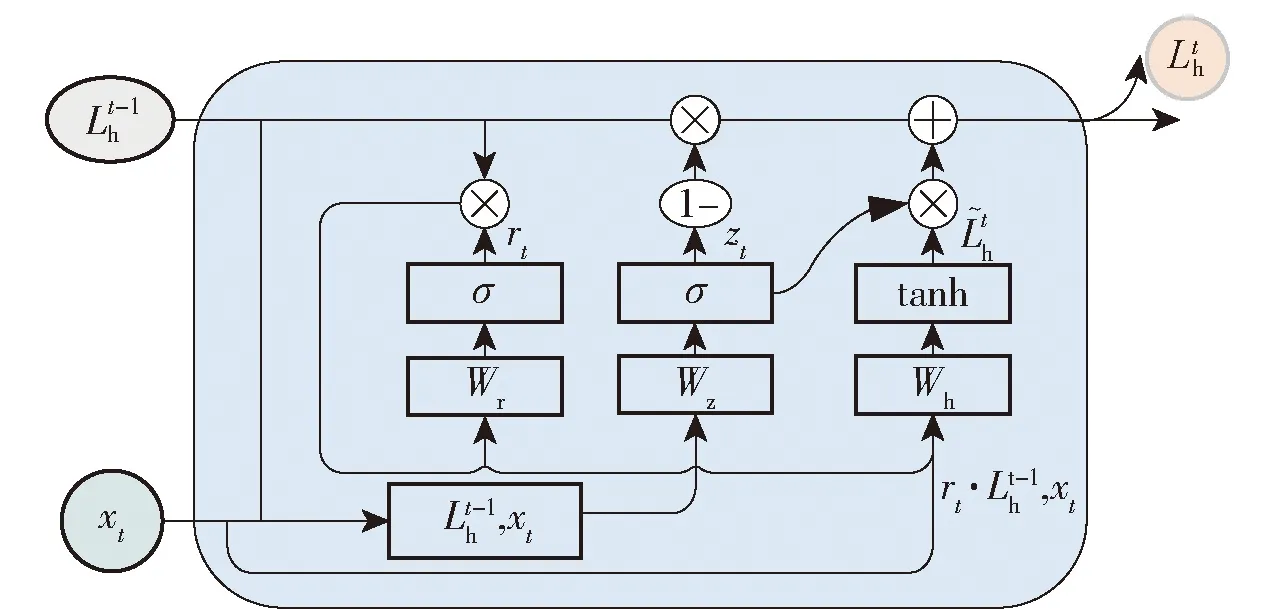
图4 GRU单元

为得到任务分配序列,需要将多个GRU单元进行串联,并将上一个时刻的输出作为下一时刻的输入,如图5所示,直到GRU产生特定长度的任务分配序列Y1∶T(T表示序列长度),即完成分配序列的生成任务。

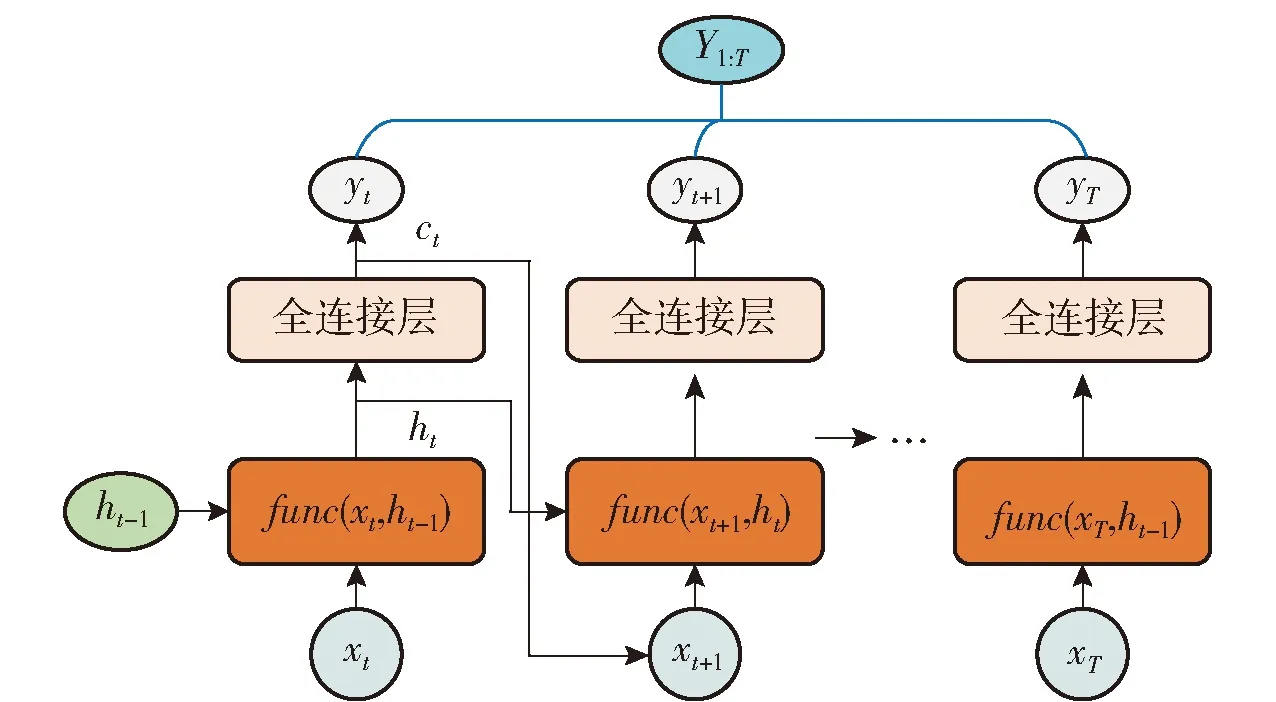
图5 序列生成网络结构

2.2 基于多层CNN的判别模型建立

生成模型生成任务分配序列后,判别模型需要判断某一序列是生成序列还是真实序列。由于近年来以CNN、RNN为代表的深度网络在进行分类问题上有较好的表现,本文建立了基于多层CNN的判别模型,其网络结构如图6所示。

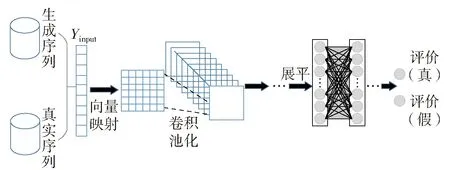
图6 判别模型结构

2.3 模型训练方法

TA-SeqGAN的训练采用生成模型和判别模型对抗训练的方式,如图7所示。

由于任务分配数据的离散性,生成模型和判别模型的更新方法不同,下文分别描述生成模型和判别模型的更新方法。

2.3.1 基于交叉熵的判别模型更新方法

TA-SeqGAN的判别模型由CNN网络搭建而成,网络输出为一个一维向量β=[μ1,μ2]∈R1×2,μi(i=1,2)分别表示输入的序列为生成序列和真实序列的概率。由式(5)可知判别模型的目标函数等价于最小化以下交叉熵函数:

min-[Ex～R[lnDφ(x)]+
Ez～Z[ln(1-Dφ(Gθ(z)))]]

(9)

式中:R为真实任务分配序列的样本空间;Z为战场信息空间;Gθ(z)为通过本文的生成模型得到的任务序列,θ为生成模型参数;Gφ(x)为将序列通过判别模型后得到的输出,φ为判别模型参数。

2.3.2 收益-评价双指导式生成模型梯度更新方法

TA-SeqGAN使用策略梯度方法进行生成模型更新,生成模型的目标函数为

(10)

然而判别模型只能对完整的序列进行评价,如果当前生成序列Y1∶t为非完整序列,则使用蒙特卡洛(MC)搜索算法[41]从策略Gβ中采样尚未生成的T-t个任务序列。定义N次MC搜索如下:

(11)

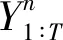
(12)

(13)

式中:{Y1∶t-1,z}表示状态信息,其中Y1∶t-1为序列状态,z为战场信息状态;J(Y1∶T|s0,y1)为生成的完整分配序列根据分配收益模型计算得到的收益值,计算方法同式(1);λ1、λ2为加权系数。

图8给出了TA-SeqGAN模型的训练算法流程。

图8 TA-SeqGAN模型训练算法

3 仿真与实验分析

3.1 实验设置

本文设定任务分配场景设置在边长50 km的矩形范围内,每次仿真随机生成三个机场位置、无人机携带资源、不同目标点坐标和目标任务需求资源。设定无人机速度为50 km/h。

本文实验采用的数据由多种群遗传算法(MPGA)生成。共进行2 000次任务分配仿真并保存任务分配方案、无人机携带资源、目标任务需求资源以及最优收益函数值以组成训练数据集。

在Pytorch 1.4架构下,以80%作为训练集、20%作为测试集,对TA-SeqGAN模型进行训练。该训练程序在AMD Ryzen 7 5800H、NVIDIA GeForce RTX 3060和16GB RAM下执行。

本文模型分两个部分进行构造:

1) 生成模型G,其特征提取网络的输入为3×NU×NT的矩阵,采用两层卷积层和两层全连接层,卷积核大小均为5×5,中间激活层采用ReLU,输出为128×1的向量;序列生成网络为GRU连接一层全连接层,隐藏空间向量大小为128×1,输入为决策向量Cs,输出为任务分配序列Y1∶T。

2)判别模型D采用CNN,设置多个不同大小的卷积核对序列分别进行卷积,以捕捉不同个数的相邻序列之间的相关性;之后对输出的所有通道分别做时序最大池化,将各个通道的池化输出值展平为向量,通过全连接层得到输出β=[μ1,μ2]∈R1×2。具体模型结构参数如表1所示。

3.2 TA-SeqGAN网络训练中超参数的选取

在GAN的训练过程中,超参数的选取对最终模型的性能至关重要,本文模型包含的超参数为每一次迭代中生成模型的训练步数g_step,判别模型的训练步数d_step,每一次训练判别模型时所用的真实数据量与生成数据量的比值ratio。为了分析以上超参数对本文模型性能的影响,首先进行训练,结果如图9所示。

图9中对比了3种情况下生成模型和判别模型各自的网络训练误差。由图9可以看出,在不同超参数情况下,生成和判别模型的训练误差在100轮左右不再有明显下降趋势,随着对抗训练的进行,生成模型和判别模型不断学习数据分布,各loss都逐渐趋于收敛,呈现出在一定范围内的振荡趋势。当用于判别模型训练真实样本数量增加时,生成模型的训练误差方差减少,生成模型误差与判别模型误差在对抗训练中同步降低,如图9(b)所示。较少的真实样本(ratio=0.3)能够使判别模型较快收敛,但由于本文生成模型的训练误差中包含了收益部分,一旦判别模型与生成模型能力相差太大,生成模型的目标就变为尽量获得高收益而不再去欺骗判别模型,生成的序列与真实序列相差太大。本文实验取g_step=1、d_step=1、ratio=1,以兼顾对抗训练与高收益值。

3.3 基于TA-SeqGAN的多场景任务分配实验

对训练好的TA-SeqGAN模型进行任务分配效果进行分析。表2给出了本节进行实验仿真分析的4种作战场景,包括无人机数量和任务数量,其中侦察任务和打击任务数量相同。作战场景包括较小规模的任务分配场景(任务数量为8、18),以及较大规模的任务分配场景(任务数量为50、80)。本节选取离散粒子群优化(DPSO)算法和MPGA进行分配收益函数指标与分配时间的对比。

3.3.1 收益函数指标比较

DPSO算法和MPGA使用的战场信息一致,种群大小为2NT,循环终止条件设置相同,即收益函数在连续10个迭代步内不再增加。首先对训练好的TA-SeqGAN模型分析其泛化性,以确保模型没有在训练数据上达到过拟合。在任务分配数量为80的大规模任务分配场景下,使用训练数据对模型进行训练后,在另一组测试数据上得到的结果如图10所示,这里测试数据的数量为100。

图10 训练数据和测试数据上的任务分配效果

由图10可以看出,模型在一批新数据(测试数据)上的结果比训练数据上的结果略低,但并未相差较大,说明模型能够应用于新数据并得到较优的结果,模型表现出较好的泛化能力。随后从小规模到大规模任务分配进行了实验,图11给出了4种分配场景下各算法进行30次任务分配仿真后得到的分配序列的收益函数指标值。由图11可以看出,TA-SeqGAN能获得与另外两种算法相近的收益函数指标值,多数场景下3种算法得到的任务分配质量相差不大,并存在TA-SeqGAN效果优于另外两种算法的情况。

图11 4种场景下各算法任务分配序列的收益函数指标值

图12给出了各算法进行30次仿真后收益函数的均值柱状图。由图12可见:在任务数量相对较少的场景下,MPGA能够生成较高质量的任务分配序列,TA-SeqGAN算法与之相比存在一定差距;随着任务数量的增加,TA-SeqGAN与MPGA算法和DPSO算法之间的差距不断减小,在任务数量较多的任务分配场景下,TA-SeqGAN进行任务分配的收益超过MPGA算法,与DPSO算法相当,仅与DPSO算法相差3%,验证了TA-SeqGAN算法在大型任务分配场景下进行任务分配的可行性。

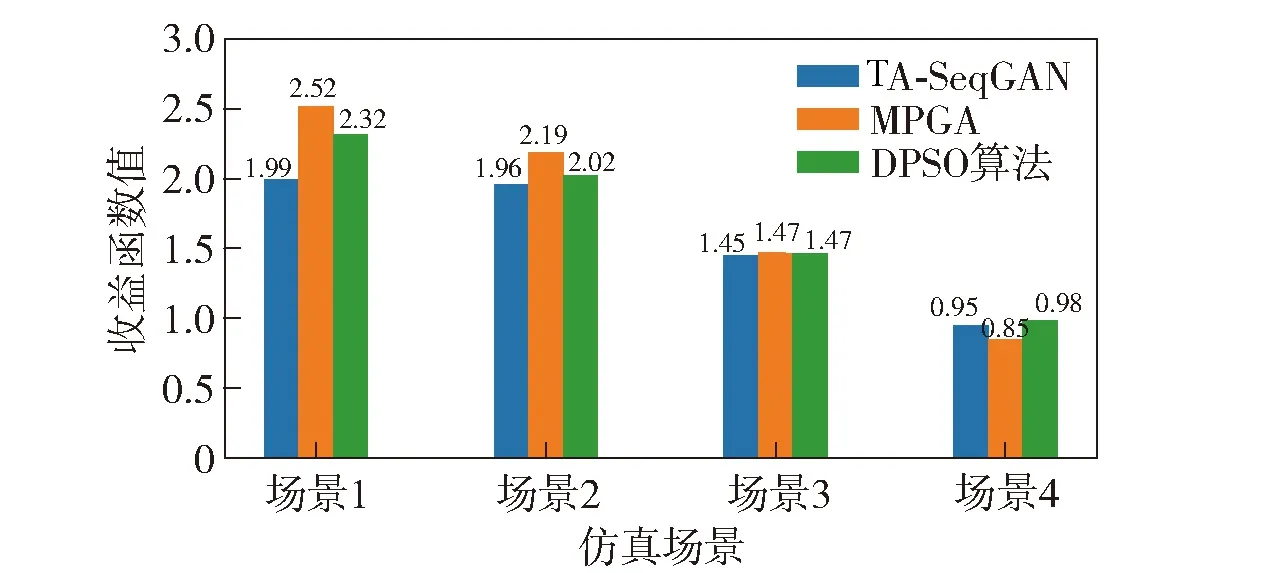
图12 各算法收益指标均值

3.3.2 算法时间消耗比较

在TA-SeqGAN模型训练完成后,在读取战场信息后能够在极短的时间内得到与之对应的任务分配序列。本文用不同的战场信息与目标数进行模拟,记录了各自算法的运行时间。表3为进行100次仿真模拟的各场景平均时间。

表3 不同场景下不同算法运行时间对比

在实验的4个场景中,随着任务数量的增多,各算法进行任务分配所消耗的时间也不断增加。在任务数量较少的场景(任务数量为8),PSO算法与TA-SeqGAN进行任务分配时间相近,GA远高于前两者;随着任务数量增多,GA和PSO算法消耗时间不断增加,当任务数量达到80时,PSO算法耗时已超过100 s,而TA-SeqGAN所耗时间几乎没有增加,远远小于PSO算法和GA。从图13中可以直观看出不同任务数量时各算法求解时间的变化趋势:在不同场景下,TA-SeqGAN的运行时间几乎保持在200 ms左右,大大低于DPSO算法和MPG;DPSO算法和MPGA的时间随着任务数量的增加呈近似指数增长,而本文算法的运行时间相对稳定。由此可见,TA-SeqGAN从小规模到较大规模的任务分配上都表现出较高的求解效率。

图13 不同分配规模下各算法运行时间对比

结合收益函数指标和时间消耗来看,TA-SeqGAN在小规模和大规模的任务分配时都能有较好的表现,尤其在求解大规模的任务分配问题时,生成的任务分配序列质量与DPSO算法和MPGA相当,但在时间消耗上远远低于这两种算法。因此,通过上述实验比较,本文提出的基于生成式对抗网络的无人机群任务分配方法适用于大型任务分配场景。