面向多无人平台区域监视任务的信息素正向激励栅格方法
2023-10-07陈亚萍王楠洪华杰刘召阳闫响达
陈亚萍, 王楠, 洪华杰, 刘召阳, 闫响达
(国防科技大学 智能科学学院, 湖南 长沙 410000)
0 引言
城市作战是现代战争的主要形式之一,也是未来战争的重要作战样式。城市具有纵横分布的街巷,高耸、密集而坚固的建筑物以及复杂的地下工程设施,作战条件恶劣,因此需要沿街巷或地下工程设施侦察监视。区域监视是对特定区域进行侦察监视以及时获取动态环境信息的一类经典问题,例如定期获取活动目标的位置信息、地形变化信息或与某些节点信息交互,其研究对于城市战场情报侦察监视具有可观的军事意义和应用价值。这类任务的完成通常需要耗费巨大的人力且在特定场合具有一定的危险性,利用多机器人系统执行该类任务成为优选方案[1]。传统区域监视通常利用以一定密度布置在区域中的传感器网络覆盖整个任务空间[2-5],这种静态监控方法往往存在感应范围固定、有感应盲区、效费比等问题。采用多无人平台协同监控时,各无人平台携带传感器移动,能动态覆盖任务区域而获取全局信息,可大大提高效费比、提高重点区域关注度。
区域监视任务追求最大访问频率以减少两次访问之间的时间差。为最大限度地扩大覆盖范围,需要不断访问地图中的所有地方,以收集环境信息,进而判断是否发生事故或异常情况[6-7]。基于图的环境表示是巡逻领域的主要模型,文献[8-10]使用由节点和边组成的无向图对环境建模。当一个环境中没有确切的重要位置而整个区域都需要巡逻时,可以使用占用网格[11-19]对环境建模。其中每个网格可以是自由的,也可以被机器人或障碍物占据,决策时选择相邻4个网格中的一个作为无人平台下一步的目标位置。Nigam等[13-15]为每个网格设置空闲时间,表示自上次访问该网格以来所经过的时间,持续监测的目标是将所有网格的最大空闲时间降至最低,提出了一种考虑全局最值的半启发式控制策略并给出了推导过程。文献[16-17]通过将值增加1个单位来计算每个可访问网格的空闲时间,网格被访问时的空闲时间重置为零。文献[18]寻求局部最小值,利用信息素的剩余量作为空闲时间的指示器,将智能体的行为定义为信息素梯度的下降,智能体向含有较少信息素的网格移动,仅考虑智能体附近的4个相邻网格。Almeida等[20]通过考虑节点的空闲度和机器人当前位置与其目标节点之间的距离来增强控制策略。Portugal等[21]对考虑局部最优的自反应(CR)方法、启发式自反应(HCR)方法、考虑全局最优的启发式寻路自认知(HPCC)方法、通用图的循环(CGG)算法和多级子图巡视(MSP)5种具有代表性的巡逻方法进行了评估。
现有方法大多仅考虑全局信息或局部信息,并且为使多个无人平台容易分散开地巡逻,通常将多个机器人的初始位置分散布置,忽略了实际应用中由于执行任务的需要、工作效率、任务衔接或环境复杂等因素导致多个无人平台的位置彼此邻近的情况,尤其是在有障碍环境中多无人平台位置邻近时不易分散开以至于发生规划层面的冲突,包括分配到同一目标位置或相邻两个无人平台交换当前位置。
本文尝试对现有控制策略进行改进,以解决环境复杂且多地面无人平台初始位置邻近场景下分散巡逻的监视问题。考虑局部因素,为半启发式控制策略引入栅格法[22]来分配单步目标位置;沿用半启发式控制策略中对距离的考量,无人平台的行为仍是趋向全局最大值的网格以分配全局目标位置,综合考量全局因素和局部因素,同时引入信息素改进目标函数并设置规则解决冲突问题,从而构建出信息素正向激励栅格法。
1 问题描述
由于城市作战的环境包含窄巷、各种形状的路口、建筑物等特征或者执行任务的需要,多无人平台在巡逻过程中可能难以避免地出现位置相近的情况。为及时获取变化的战场信息,应尽可能使无人平台分散巡逻并避免有网格长时间没有被访问到,以提高资源利用率和对目标空间的访问效率。为此,有必要研究多无人平台在环境复杂且位置相近时的分散巡逻策略。
1.1 问题建模
多无人平台在二维环境中持续地移动,每个无人平台上载有用于观测环境的传感器,无人平台之间信息共享。
1)目标空间。目标空间为划分成g×g个网格的正方形区域,每个网格以其中心处的坐标(i,j)为位置坐标,每个网格的边长为单位值1。目标空间中的网格分为被障碍物占据的占用网格和未被占据的自由网格。
2)n个无人平台。假设无人平台只能处在网格的中心处或在从一个网格中心移向另一个网格中心的路上,将时间离散化为时间点,在任一时间点无人平台k(k=1,2,…,n)位于其相应的位置上。由于在无人平台到达全局目标位置前,其余无人平台可能已经访问该位置,每个无人平台每到达一个网格,便为其重新分配全局目标位置和单步目标位置。
如图1所示,10×10大小的目标空间中19个黑色占用网格,自由网格中的数字用于表示2.1节的空闲时间或2.2节的信息素值。黑三角形、黑矩形和黑圆形分别表示无人平台。图2为两个无人平台位置相邻时规划层的冲突情况,所分配的目标位置为彼此的当前位置,A、B为两个平台。

图1 网格表示的环境模型

图2 相邻无人平台位置交换示意图
1.2 假定条件
为简化计算模型,定义如下约束:
1)忽略无人平台的质量、形状、构造、动力学特性以及转弯产生的影响,将无人平台视为质点。
2)无人平台每次只移动一个网格,在连续的时间点之间,每个无人平台只能从一个网格移动至与其相邻的网格。
3)每个无人平台的传感器观测范围等于单个网格的面积,无人平台处于网格(i,j)时,网格(i,j)便被该无人平台观测到且视为被访问一次,多无人平台占用同一网格时对该网格的访问次数视为一次。
4)每个无人平台的移动方向为上下左右4个方向,无人平台之间在移动时避开彼此,不发生碰撞行为。
5)约定两个无人平台相邻包括如下情形:两个无人平台之间的曼哈顿距离小于等于2。
1.3 评估标准
评估标准在巡逻问题中起着两个作用:作为比较不同巡逻策略时性能的衡量标准,或作决策时的参考因素。现有标准主要关注节点两次访问之间的时间间隔、成本和收益的权衡以及多机器人系统的特性,以评估其对动态情况的适应性[5]。Machado等[23]提出了许多基于空闲时间的概念,即任何巡逻机器人连续两次访问同一节点之间的未访问时间,并从全局或局部、历史或实时的角度定义了节点瞬时空闲、瞬时图空闲和最坏空闲等特定标准。
本文使用全局平均空闲时间并提出冲突占比之和这一新的评估标准,对本文关注的不同控制策略进行比较。
节点在时间步w=t时的空闲时间Idl(t)为
Idl(t)=t-th
(1)
式中:th表示节点最后一次被访问的时间步。
节点在时间步w=t时的平均空闲时间Idla(t)为
Idla(t)=(Idla(tp)·Freq+Idl(t))/(Freq+1)
(2)
式中:Idla(tp)表示上一时间步的节点平均空闲时间;Freq为节点被访问次数。
节点在时间步w=t时的最大瞬时空闲时间Idls(t)为
(3)
式中:Idlnum(ti)表示时间步w=ti时节点num的空闲时间;Z为自由网格数量;t1为统计最大瞬间空闲时间的初始时间步。
节点在时间步w=t时的全局平均空闲时间为
(4)
冲突占比之和P为
(5)
式中:Ck表示无人平台k的冲突占比;nk表示无人平台k的总冲突次数;W为总迭代次数;Cp表示经历总迭代次数W的所有无人平台所发生的冲突次数之和,每次迭代计算一次全局目标位置和单步目标位置。
2 方法和原理
本文信息素正向激励栅格法是在半启发式控制策略的基础上与栅格法相结合,引入信息素和冲突消解规则而产生的。
2.1 半启发式栅格法
2.1.1 半启发式控制策略
为每个网格设置空闲时间,该空闲时间表示网格自上次被访问以来所经过的时间,值越大表示网格没有被访问的时间越长,因此持续监控的目标是将最大空闲时间降为最低。对单个无人平台而言,全局目标位置应是具有最大空闲时间的网格,无人平台到达全局目标位置后该网格的空闲时间Ap被置为零,在这一路径中无人平台所经过网格的空闲时间在被访问时也被置为零,即
(6)
由于多个无人平台距离具有最大空闲时间的网格远近不同,多个无人平台之间的相对位置会影响对网格的选择,此时控制策略可以通过为每个网格设置导向值来表示,无人平台与网格之间的距离以及其余无人平台与网格之间的距离会影响网格的导向值。为无人平台k选择全局目标位置时,计算所有网格的导向值并选择具有最大导向值的网格,即
(7)
式中:Vi,j表示网格(i,j)的导向值;Ai,j为网格(i,j)的空闲时间;ω0和ω1为加权参数,ω0=-1/v,ω1=-1/v,v为无人平台的速度;δk为无人平台k与网格(i,j)之间的距离;δn为其余无人平台与网格(i,j)之间的距离。
δk按下式计算:
δk=|px-i|+|py-j|
(8)
式中:(px,py)为无人平台k当前位置的坐标;(i,j)为网格的坐标。
min(δn)按下式计算:
min(δn)=min(|p1x-i|+|p1y-j|,…,|pnx-i|+|pny-j|)
(9)
式中:(p1x,p1y),…,(pnx,pny)为除无人平台k以外其余无人平台的当前位置坐标。
将上述方法应用于本文的有障碍环境,令占用网格的导向值Vi,j为极小的常数:
Vij=-10 000
(10)
但仅改变有障碍网格的值Vi,j并不能使无人平台完全避开占用网格。这是因为Vi,j用于计算无人平台的全局目标位置,将Vi,j赋极小值只能保证不会将该网格选作无人平台的全局目标位置,无人平台在朝着全局目标位置移动的过程中仍然可能经过该占用网格,因此有必要寻求一种避障方法。
2.1.2 栅格法
为避开占用网格,无人平台需要从相邻网格中选择合适的网格作为单步目标位置。文献[22]所提栅格搜索算法步骤如下:
步骤1确定起始位置、全局目标位置和占用网格。
步骤2搜索无人平台的相邻网格并选出自由网格。
步骤3利用评价函数h来计算自由网格(i,j)与全局目标位置(i′,j′)之间的距离:
(11)
步骤4选取与全局目标位置之间的距离最小的自由网格,并将其作为无人平台的单步目标位置。
试验时发现直接应用栅格法时,无人平台会“穿过”占用网格,这是不被允许的。因此对栅格法进行如下改进:如果选出的最优自由网格刚刚被访问过,则选择次优的自由网格,即与全局目标位置之间的距离第二小的自由网格。图3所示为加入栅格法前后的效果,线段表示无人平台的大致移动轨迹。

图3 加入栅格法前后的对比图
利用半启发式控制策略结合栅格法构建半启发式栅格法(SGM),并在无人平台每走至一个网格时重新计算全局目标位置。算法流程如下:
步骤1初始化目标空间大小g、无人平台数量、速度和初始位置、占用网格位置以及网格空闲时间。
步骤2执行如下循环:
①计算各个无人平台的当前位置与各自由网格之间的距离;
②对单个无人平台而言,计算其余无人平台的当前位置与各自由网格之间距离的最小值;
③为占用网格的导向值赋值-10 000;
④每个无人平台根据式(7)计算其对应的各个自由网格的导向值,并选择具有最大导向值的自由网格作为其全局目标位置;
⑤对每个无人平台使用栅格法,执行2.1.2节中的步骤;
⑥当无人平台到达单步目标位置后,根据式(6)将对应网格的空闲时间清零。
为避免将同一个全局目标位置分配给不同的无人平台,在计算无人平台对应网格的导向值时,选出次最大导向值的网格,出现重复分配的情况时将次最大导向值的网格作为新的全局目标位置。
2.2 信息素正向激励栅格法设计
2.2.1 信息素
自然界中具有探索价值的地方往往沉积较多的信息素,信息素的正反馈使得蚂蚁倾向于沿着信息素多的路线行进,随着探索区域价值的变化,信息素的沉积量也会改变。受此启发,对目标空间网格分解后为每个网格预设相应的信息素,假定所有自由网格的初始信息素相同。将无人平台对网格的访问结果视为信息素的衰减,被无人平台访问过的网格其信息素会减小一定值,未被访问的网格其信息素增加一定值。只要有一个自由网格一直没有被无人平台监测过,则该网格的信息素值就大于其他网格的信息素值。因此无人平台趋向于朝着信息素值大的网格行进。
坐标为(i,j)的网格当前信息素表示为
(12)
式中:α为与距离、网格重要度有关的衰减系数,α∈(0, 1);β为沉积系数,β>1;Celli,j的单位为与时间有关的量纲,本文中取s。选择最大导向值的网格作为无人平台的全局目标位置:
(13)
2.2.2 冲突消解规则
栅格法虽然解决了将占用网格分配给无人平台的问题,但多个无人平台的位置彼此邻近时,不同无人平台可能分配到同一个自由网格,并在之后保持规划轨迹重合,影响资源利用率和巡视效率。为此,本文研究多无人平台执行持续监控任务中的运动协调问题,冲突消解的主要目标是减少目标位置在分配过程中的冲突,使无人平台尽量分散开地探测环境。对单个无人平台如何到达分配的目标位置,在向着目标位置移动过程中如何避障这些不作研究。图4所示为冲突消解原理图。

图4 冲突消解原理图
为解决冲突问题,依照以下规则选择单步目标位置:
当两个无人平台相邻时,每个无人平台选择回头,单步目标位置为前一步到达的网格:
U(u,t)=Idl(t)min
(14)
式中:U(u,t)为确定无人平台单步目标位置u的效用函数;Idl(t)min表示无人平台当前位置的相邻自由网格中的最小空闲时间。
当无人平台没有与其他无人平台相邻时,若其相邻自由网格数量大于1则禁止回头,单步目标位置为除前一步到达的网格之外的距离全局目标位置最近的网格:
U(u,t)=hmin
(15)
式中:hmin表示无人平台的相邻自由网格中与全局目标位置之间的最小距离。
自循环是指无人平台的规划轨迹构成闭合矩形,如图5所示。

图5 自循环判断示意图
图5中,无人平台当前位置为p1,自循环可能发生在p1p2p3p4、p1p4p′3p′2、p1p′4p″2p′2和p1p′4p″3p2中的其中一个矩形,根据无人平台最近3次分配的单步目标位置为矩形的3个顶点,判断无人平台处于自循环。当无人平台发生自循环时,若除该4个网格之外的网格中存在与无人平台前进方向一致的网格,则单步目标位置为该网格,否则选择除该4个网格之外的任一可到达网格:
发生自循环p1p2p3p4时,p1的两个相邻网格p2、p4为自循环矩形中的点,选择另外两个相邻网格p′2、p′4中信息素大的网格作为单步目标位置:
(16)
无人平台当前位置为p2且发生自循环p1p2p3p4时,若相邻自由网格为3个,则选择另外一个相邻自由网格p″3为单步目标位置:
u=p″3,Nf={p1,p3,p″3}
(17)
式中:Nf为相邻自由网格集合。
若无人平台当前位置的相邻自由网格均在自循环矩形中,则选择自循环矩形中的任一可到达网格,直到可以分配自循环矩形以外的相邻自由网格为止。以无人平台当前位置在p3且自循环为p1p2p3p4为例:
u=p2∨p4,Nf={p2,p4}
(18)
2.2.3 信息素正向激励栅格法
将信息素和上述规则引入半启发式栅格法,形成信息素正向激励栅格法(PPIGM),对应的多无人平台持续监控控制流程如图6所示。

图6 持续监控流程示意图
同一个无人平台可能计算出多个全局目标位置,多个无人平台的全局目标位置也可能相同,因此采用如下次优分配过程:
同一个无人平台存在多个全局目标位置时,选择距离该无人平台最近的一个全局目标位置;不同无人平台计算得到同一个全局目标位置时,为距离该全局目标位置远的无人平台分配次优目标位置,次优目标位置为该无人平台计算得到的次大导向值网格。
加入信息素的SGM与次优分配过程完成了无人平台全局目标位置的分配,利用冲突消解优化无人平台单步目标位置的选择。
3 试验结果及分析
3.1 试验模型和参数选取
如图7所示,仿真环境为10×10的二维网格空间,每个网格的边长为单位值1,黑色网格表示占用网格,障碍物数量分别为OBS=19、OBS=13和OBS=6,自由网格数量分别为Z=81、Z=87和Z=94。自由网格的数量不同表示通道的弯曲复杂程度不同,以对比通道变化对算法性能的影响。情景1中无人平台的初始位置分别为(8, 4),(6, 3),(7, 2);情景2(见图8)中无人平台的初始位置分别为(1, 1),(6, 3),(4, 2)。式(7)中Ai,j初始值为0,网格(i,j)被访问前Ai,j每单位时间步增1,一旦被访问Ai,j则置为0。式(12)中α=0.9,β=1.1,ω0=-1,ω1=-1。
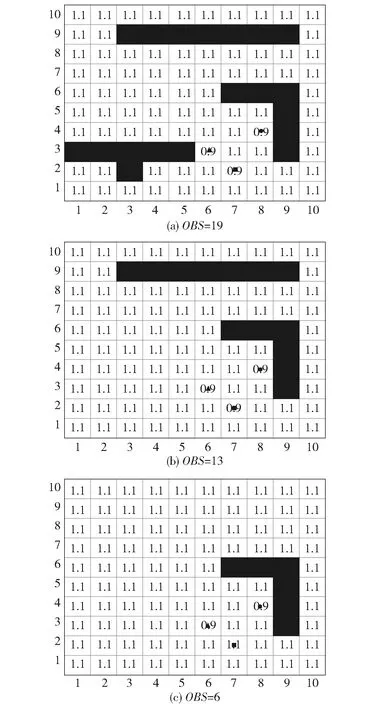
图7 不同障碍物数量的情景1

图8 不同障碍物数量的情景2
图9展示了两种情景Z=81时的轨迹图。由图9 可见,无人平台的初始位置不同,规划轨迹也不相同。下面分别在两种情景下开展试验,将PPIGM与SGM、文献[21]中的CR、HCR、HPCC(Dijkstra算法改用A*算法)以及文献[18]中的EVAP、CLInG进行对比试验,其中HCR在本文环境模型下退化为CR,因此实际上是与SGM、CR、HPCC、EVAP、CLInG进行对比。
3.2 与现有控制策略对比
分别从冲突占比之和与全局平均空闲时间两方面对比不同算法的性能。
3.2.1 情景1
表1为OBS=19、OBS=13和OBS=6共3种 条件下不同算法迭代次数W=1 000的冲突占比之和。由表1可见:试验中CR和HPCC一直出现两个无人平台冲突的情况,其次为EVAP和CLInG,表现较优的为SGM(冲突占比之和为20%左右),PPIGM的冲突占比之和为0.1%,表现最优;在障碍物数量变化时PPIGM的表现适应性好,冲突占比之和始终保持为0.1%;SGM也随障碍物数量的增加冲突占比之和减小;EVAP和CLInG虽然在OBS=19时冲突占比之和有所下降,但整体而言仍保持较高的冲突占比之和,造成这一波动的原因在于EVAP和CLInG包含随机机制。
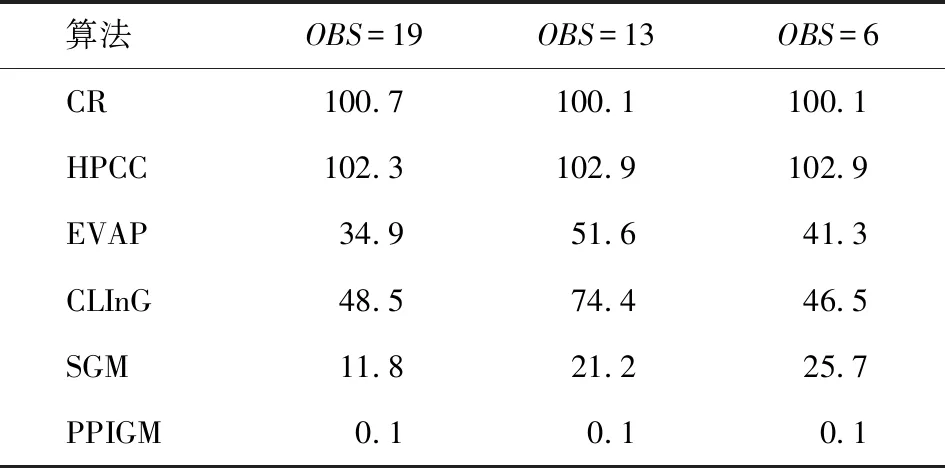
表1 情景1 OBS取不同值时的冲突占比之和
图10为OBS=19、OBS=13和OBS=6共3种条件下不同算法全局平均空闲时间随迭代次数的变化。由图10可见:障碍物数量较多时PPIGM的全局平均空闲时间明显小于SGM,特别当OBS=19时SGM没有收敛,这是因为在后期无人平台陷入局部区域而无法走出,也是冲突占比之和低的原因;整体而言CR和HPCC的最终全局平均空闲时间较大,PPIGM、EVAP和CLInG的最终全局平均空闲时间较小,表现较好。
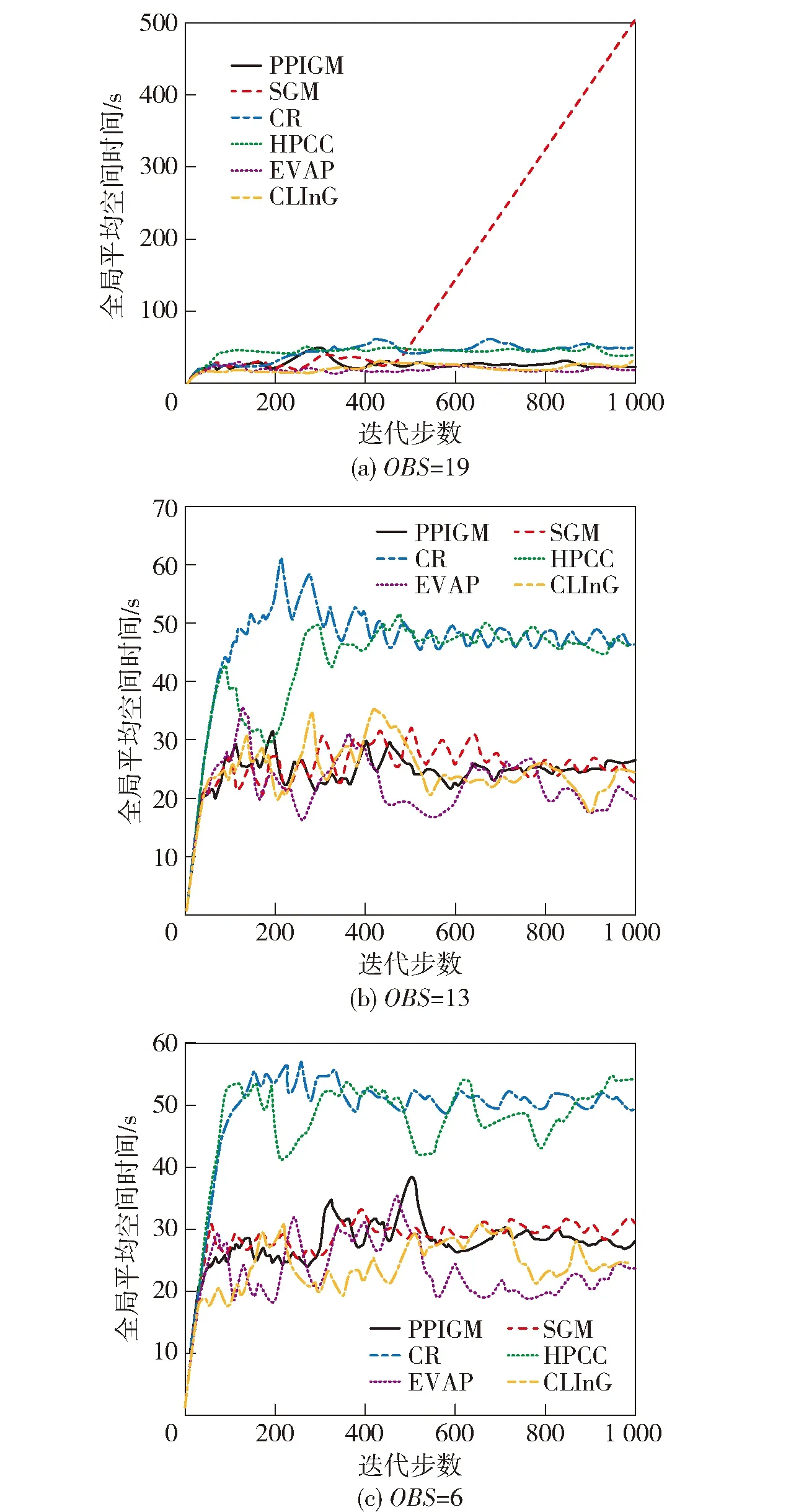
图10 情景1不同算法的全局平均空闲时间对比图
图11给出了PPIGM与现有5种算法在全局平均空闲时间上的分布随障碍物数量的变化情况。由图11可见:PPIGM的全局平均空闲时间比较接近正态分布,现有算法的分布特性基本上呈偏态分布;SGM在OBS=19时的分布最为分散;CR和HPCC的分布情况次于PPIGM、EVAP和CLInG,这些表现与图10吻合;PPIGM的箱体宽度小于EVAP和CLInG,表明PPIGM的分布更为集中。
3.2.2 情景2
表2为OBS=19、OBS=13和OBS=6共3种条件下不同算法总迭代次数W=1 000的冲突占比之和。由表2可见,各算法表现与情景1大致相同,PPIGM的冲突占比之和较为稳定地保持在很小的水平。值得注意的是,EVAP随障碍物数量的增加冲突占比之和增大,CLInG虽然在OBS=19时冲突占比之和略微下降,但整体而言仍保持较高的冲突占比之和。

表2 情景2 OBS取不同值时冲突占比之和
图12展示了OBS=19、OBS=13和OBS=6共3种条件下不同算法的全局平均空闲时间随迭代次数的变化。由图12可见:各算法的表现与情景1大致相同。障碍物数量较少时PPIGM的全局平均空闲时间有较大峰,但在后期能够降下来,证明PPIGM能够跳出局部区域,为克服SGM陷入局部区域的缺陷提供了可能;整体而言,CR和HPCC的最终全局平均空闲时间较大,PPIGM、EVAP和CLInG的最终全局平均空闲时间较小,表现较好。
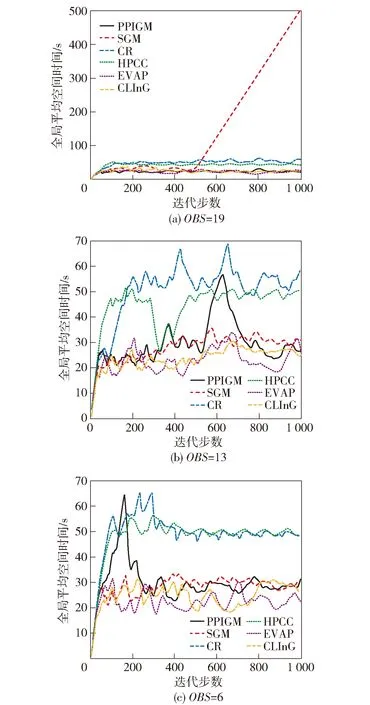
图12 情景2不同算法的全局平均空闲时间对比图
图13给出了不同算法在全局平均空闲时间上的分布随障碍物数量变化情况,从中可见各算法的表现与情景1大致相同。
3.3 小结
1) PPIGM在冲突消解上的表现优于现有控制策略且在全局平均空闲时间上的表现较优,这是因为PPIGM根据全局目标位置分配单步目标位置,综合考虑了冲突消解和空闲时间的因素,而根据无人平台在冲突时的反应规则,难以避免地要牺牲掉部分空闲时间;
2) PPIGM全局平均空闲时间的分布整体趋近正态分布,且相较于现有控制策略分布较为集中,这是因为现有控制策略均只考虑全局目标位置或只考虑单步目标位置,导致数据分布偏态较重也较为分散。
4 结论
本文对复杂环境中多无人平台初始位置邻近情况下的持续监控方法进行研究,在半启发式控制策略和栅格法的基础上通过引入信息素改进了目标函数,并制定冲突消解规则,从而构建出信息素正向激励栅格法。得出以下主要结论:
1) PPIGM能够很好地解决多无人平台在复杂环境且位置邻近时的冲突问题,全局平均空闲时间与现有方法相比也较好。
2) PPIGM对障碍物数量变化的适应性较好,在冲突消解和全局平均空闲时间上的综合表现较为优越。
本文研究结果对后续研究工作和应用均具有极强的指导意义和参考价值。受限于当前条件,本次试验是在特定参数(n=3,α=0.9,β=1.1,ω0=-1,ω1=-1)下进行的,参数变化对PPIGM的性能影响有待研究;此外PPIGM中包含随机机制,大量试验样本情况下PPIGM的性能表现也值得关注。
